Journal of Quantum Information Science
Vol.05 No.01(2015), Article ID:55023,7 pages
10.4236/jqis.2015.51004
A Fractal Rindler-Regge Triangulation in the Hyperbolic Plane and Cosmic de Sitter Accelerated Expansion
Mohamed S. El Naschie
Department of Physics, University of Alexandria, Alexandria, Egypt
Email: Chaossf@aol.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 December 2014; accepted 24 March 2015; published 25 March 2015
ABSTRACT
The well known finite elements Regge calculus is transformed to a triangulation in the hyperbolic plane using fractal Rindler wedges as tiling elements. The final result is an expanding de Sitter hyperbolic, i.e. Gauss-Bolyai-Lobachevsky universe with dark energy and ordinary energy densities in full agreement with cosmic observations and measurements. In the course of obtaining this vital result, the work addresses fundamental points connected to a host of subjects, namely Hardy’s quantum entanglement, an extension of Turing’s machine to a transfinite version, the phenomenon of measure concentration in the context of Banach-like spaces with high dimensionality as well as the pioneering work on the relation between quantum entanglement and computational efficiency.
Keywords:
Component, Hyperbolic Regge Calculus, Finite Elements in Cosmology, de Sitter Universe, E-Infinity Theory, Transfinite Turing Golden Mean Computer, Rindler Triangulation, Endophysics, Anti-Bethes Poof, Topological Quantum Entanglement, Gauss-Bolyai-Lobachevsky Geometry

1. Introduction
Regge calculus is a powerful finite element-like method in four dimensions applied to solve Einstein’s highly nonlinear equations [1] -[13] . The method was further developed, modified and extended to a quantum gravity theory by many researchers [3] . In recent times the work of J. Ambjorn and R. Loll [13] deserves special attention [1] - [3] [13] . It was against this background that the present work was planned and executed by transforming Regge calculus to a fractal hyperbolic theory [14] which is used to solve the mystery of accelerated cosmic expansion and the associated dark energy believed to be an expression of a non-vanishing cosmological constant [14] - [24] . In short, the spacetime of our theory is a hyperbolic fractal where quantum entanglement is replaced by a Hardy type natural topological zero measure entanglement [22] following E-infinity theory [24] - [35] .
The paper is subdivided for efficient reading as follows: After the Introduction we review in Section 2 some important dualities between inverse electroweak couplings and the various energy sections as well as the extension of Turing’s machine to a transfinite version via a highly structured golden mean ring as a number system [34] - [48] . Section 3 is a condensed account of the Regge “finite element” method and its adaption to the present work [35] . In Section 4 we discuss the ideas and hunches leading to a hyperbolic expanding de Sitter universe [35] . Subsequently in Section 5 the fundamental results are wrapped up with the analogy presented earlier in Section 2 [49] - [60] . Finally in Section 6 we present a short recapitulation of the paper and the relevance of quantum entanglement enhanced computation [61] - [63] .
The present work is by no means self contained but we rely on an adequate list of references to fill in the inevitable gaps in a condensed presentation [20] - [63] .
2. E-Infinity Dualities between Various Cosmic Energy Sections and Electroweak Couplings―The Transfinite Turing Machine
Let us consider here a most instructive and somewhat surprising duality between the coupling constant of the electroweak interaction (i.e.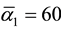 ,
,
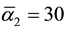 ,
,
 and
and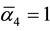 ) [25] - [40] and the four fundamental sections of cosmic energy (i.e. pure dark energy 74%, dark matter 22%, ordinary energy 3% and ordinary matter 1%) [14] - [24] . The values mentioned above for
) [25] - [40] and the four fundamental sections of cosmic energy (i.e. pure dark energy 74%, dark matter 22%, ordinary energy 3% and ordinary matter 1%) [14] - [24] . The values mentioned above for
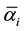 are the exact E-infinity theoretical value which are very close to the experimental one [25] - [32] and also satisfies the reconstruction equation of
are the exact E-infinity theoretical value which are very close to the experimental one [25] - [32] and also satisfies the reconstruction equation of
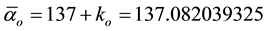 where
where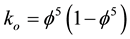 ,
,
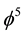 = P (Hardy’s quantum entanglement) and
= P (Hardy’s quantum entanglement) and
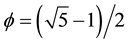 [22] . Inserting in the said equation one finds [28] [33]
[22] . Inserting in the said equation one finds [28] [33]
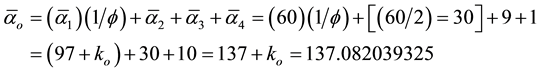 (1)
(1)
where
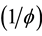 is the E-infinity Clebsch factor [25] - [27] [39] and
is the E-infinity Clebsch factor [25] - [27] [39] and , where
, where
 is Hardy’s probability of quantum-topological zero measure entanglement [22] , could be expressed in terms of ‘tHooft’s order parameter of dimensional regularization, namely
is Hardy’s probability of quantum-topological zero measure entanglement [22] , could be expressed in terms of ‘tHooft’s order parameter of dimensional regularization, namely
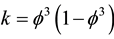 to give
to give . On the other hand, the integer value of
. On the other hand, the integer value of
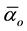 namely
namely
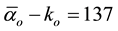
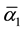


In addition the E-infinity transfinite value the Clebsch factor [39] must be made rational, i.e.

We note on passing that the Clebsch factor is needed because the electroweak is based on three different Lie symmetry groups U(1), SU(2) and SU(3) [39] [40] which are made compatible by this very same factor. Inserting in our renormalization equation one finds

where 22 + 4 = 26 is the dimensionality of the Veneziano-Nambu bosonic string space [39] . It is also noteworthy that [11] [12] [19] [20]

and similarly
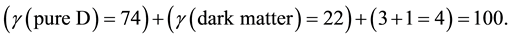
From the preceding elementary analysis, it is obvious even to non-mathematicians that the mathematical scheme behind this calculation is trying to tell us something which transcends mathematics in the common naïve understanding as a mere tool and elevate it to something indistinguishable from physics, albeit the physics of what G. ‘tHooft calls the elementary building block of space, time and matter [41] . Let us attempt in good faith to translate what is superficially numbers to what is equally superficially means physics. Since 75% corresponds to
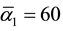

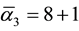
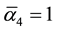
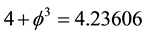

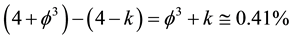
3. From Transfinite Triangulation in the Hyperbolic Plane to Dark Energy
In what follows, we give a concise outline for a general theory of quantum relativity and dark energy based on an exact transfinite extension of Regge triangulation calculus in the Poincare-Beltrami hyperbolic plane [39] . In our present theory, not only the basic idea is very easy to grasp but also the actual computation is surreal in its simplicity [14] . We suggest starting by recalling the geometrical shape of a circular region covered by triangular tiles which are a crossbreed between those used in Klein’s modular curve and those utilized in Penrose tiling [19] [20] [39] . Compactifying these shapes would mean that we are approaching a fractal Penrose universe or in more stringent mathematical terminology, our circular region becomes an exact realization of a fiber bundle manifold [39] or in the language used by A. Connes, a noncommutative x quotient space [36] . It is thus neither difficult to imagine nor mathematical to reason that the following applies to the topology and geometry we are dealing with:
1) In the center of our Regge “finite elements” tessellation [1] - [5] , the triangular tiles are rather ordinary classical shapes with straight sides. However, as we move from the center of the Beltrami-Poincaré plane outwardly the triangular straight lines start to deform and shrink hyperbolically [35] [39] .
2) The circular boundary lies naturally at infinity and the area of the hyperbolic triangle tends towards a classical zero.
3) Adding uniform randomness to the so obtained fractal Regge tiling covering of the hyperbolic plane will result in a topology endowed with the golden mean inherited from the two legitimate parents, namely the Mauldin-Williams random triadic Cantor sets [28] - [34] and the golden mean proportioned kite and dart of Penrose’s universe [28] - [34] [39] .
4) Having went as far as we did, our basic spacetime blocks will be looked upon not as mere hyperbolic triangles but as a Rindler triangle, i.e. Rindler wedge with the familiar spear form containing the correlated part of spacetime, i.e. the entangled part while the moon section rear part contains the uncorrelated part of space which amounts to about 95.5% of the total “area” of the Rindler wedge [14] [35] .
5) The genesis from classical triangular geometry to that of hyperbolic geometry may be likened to a very far extent with that of the logistic map which starts by period doubling classical bifurcation [48] [50] [52] but at approximately l = 3.8 we have triple bifurcation leading according to Zarkovski’s number theory to a quasi chaotic region [50] following the title of the famous J. Yorke paper “Period three implies chaos” and from l = 4.23606 onwards we enter into a hyperbolic region [48] [50] [52] . It is incredible how generic this behaviour is when we consider that the Hausdorff dimensions of ‘tHooft’s fractal regularization space is 4 − k = 3.81966011 while the core of E-infinity Cantorian spacetime is characterized by a Hausdorff dimension expectation of exactly D = 4.23606, i.e. D = l = 4.23606 of the logistic map [57] . Needless to say that in all of our physical analysis quantum entanglement is de facto replaced by the notion of a zero measure topological Hardy type entanglement [22] .
6) Also as we move away from the center with our normal triangle, we leave behind us slowly but surely an exo-physical universe and approach an endo-physical one [53] [54] . At infinity we cannot reconcile experiment with theory except when we recognize the exo-endo duality as uncovered in the pioneering work of D. Finkelstein, O.E. Roessler, H. Primas and their schools [53] [54] .
7) Most importantly, we must realize that as our random space grows more “hyperbolic” it does not acquire a negative curvature but against naïve expectation, the curvature corresponding to the entire hyperbolic projection is not negative but positive.
8) Based on the above we have to conclude that our space corresponds to a de Sitter universe [39] .
9) The preceding scenario of a de Sitter space entails not only an expanding but an accelerated expansion of the spacetime described above.
10) Taking points one to nine, we conclude that the cosmological constant is non-zero and that our universe is self similar hyperbolic fractal and that with a 95.5% volume concentration at the surface of the spacetime manifold. This is actually a mathematical theorem on volume measure concentration of convex highly dimensional Banach-like spaces.
4. Discussion and Our Initial Hunch That E-Infinity Leads to an Expanding Hyperbolic de Sitter University
It is quite instructive and rather helpful to a proper understanding of the hyperbolic fractal nature of our alleged de Sitter universe to explain how we arrived at what must have been just a hunch and foggy idea, at least initially. Any idea, no matter how simple is produced by a highly complex and as yet not really understood perceptive, combinatorial and imaginative brain process, but in the present case it may well have started by the author noticing the similarity between the Rindler wedge and the Regge triangulation used in recent times intensively in a computer oriented theory by Ambjorn and Loll [13] . In addition, we know that a normal triangle is fat in the spherical case but thin in the hyperbolic case. Therefore in the limit the area tends to zero. Furthermore as we could describe a flat space as space with a trivial axiom for parallel lines and a spherical space as zero parallel lines space, a hyperbolic space has infinitely many parallel lines just as a Cantorian space has infinitely many dimensions. The only point which may not be straight forwards in our largely hand waving but accurate arguments is that we are claiming “Rindler” tiling space will be globally a de Sitter space although on account of its hyperbolicity, it should have a negative curvature, an anti de Sitter space [39] . However, noting the intrinsic randomness coupled with the Poincare-Beltrami projection and the basic averaging used, our space is not simply hyperbolic space but actually a very high dimensional Banach-like Cantorian fractal [14] [35] which is projected on the hyperbolic plane to give us this unique structure. In the case of any doubt, the reader needs to ponder the simplicity of the exact expressions of the Rindler areas involved. These are the arrow like area which is equal to the density of ordinary energy of the exo-physical universe [53] [54] and is given by [18] -[20]
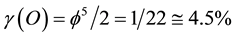
and the circular section area behind the arrow which is equal to the total ark energy density of an endo-physical universe [53] [54] , namely [18] - [20]

If the proof of the pudding is in the eating, as a common English proverb says, then the above result and the associated energy-mass relationship [18] - [20]

are sufficient proof for us that Einstein’s formula is confirmed rather than refuted by the absence of measurable dark energy and the observation of accelerated cosmic expansion as well as our present reinterpretation of E = mc2 as the sum of the measurable energy of the quantum particle E(O) and the energy of the quantum wave E(D) which we cannot measure because of the Hartle-Hawking collapse of Wheeler-Dewitt wave function of the cosmos [12] [39] . For the avoidance of any possible misunderstanding, we stress again that our dissection not only presupposes Einstein’s beautiful formula but in conjunction with the cosmic endo-physical measurement, it confirms E = mc2 theoretically and experimentally beyond a trace of a doubt.
5. Analogies between Analogies and into Deep 5 Dimensional de Sitter Waters
From the preceding analysis, we see that a most intriguing duality or maybe what we could call analogies among analogies as befitting a self affine universe exists, which we could represent as earlier in Section 2:

However, this is not yet where things end for there are some even deeper interrelationships not only between time and matter but also between mater expressed as mass and space as well as spacetime dimensionality. It turns out that a unit of dimensionless energy corresponds to a unit of Cantorian spacetime and that tangible and directly detectable mass (m) enters into our equations as a three dimensional, i.e. space-like Cantor set given by the treble intersection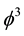
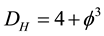

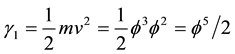
and

which then leads to the two expressions for ordinary energy


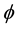
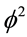

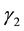




6. Conclusion
The classical Regge method of relativity is transformed using Gauss-Bolyai-Lobachevsky hyperbolic geometry to the context of quantum relativity and cosmology to give information about the accelerated cosmic expansion and the associated dark energy density. The task was achieved by transforming the method to the hyperbolic plane and using Rindler-like triangles to form a random self similar fractal tiling akin to that of Klein-Penrose. The final conclusion is that our model effectively represents a fractal de Sitter universe with ordinary measurable exo-physical energy density of

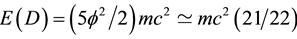
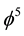
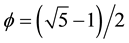
References
- Regge, T. (1961) General Relativity without Coordinates. Il Nuovo Cimento Series 10, 19, 558-571.
- Regge, T. and Wheeler, J.A. (1957) Stability of Schwarzschild Singularity. Physics Review, 108, 1063. http://dx.doi.org/10.1103/PhysRev.108.1063
- Misner, C., Thorne, K. and Wheeler, J. (1973) Gravitation. Freeman, New York.
- El Naschie, M.S. (2007) The Fibonacci Code Behind Superstrings and P-Branes. An Answer to M. Kaku’s Fundamental Question. Chaos, Solitons & Fractals, 31, 537-547. http://dx.doi.org/10.1016/j.chaos.2006.07.001
- El Naschie, M.S. (2013) The Quantum Gravity Immirzi Parameter―A General Physical and Topological Interpretation. Gravity and Cosmology, 19, 151-153. http://dx.doi.org/10.1134/S0202289313030031
- El Naschie, M.S. (2005) Einstein’s Dream and Fractal Gravity. Chaos, Solitons & Fractals, 24, 1-5. http://dx.doi.org/10.1016/j.chaos.2004.09.001
- El Naschie, M.S. (2001) Fisher’s Scaling and Dualities at High Energy in E-infinity Spaces. Chaos, Solitons & Fractals, 12, 1557-1561. http://dx.doi.org/10.1016/S0960-0779(00)00127-2
- Argyris, J., Ciubotariu, C. and Weingartner, W.E. (1999) Progress in Physical Concepts and Strings and Superstring Theory―Thirty Years of String Theory. Chaos, Solitons & Fractals, 10, 225-256. http://dx.doi.org/10.1016/S0960-0779(98)00320-8
- Marek-Crnjac, L. and El Naschie, M.S. (2013) Chaotic Fractal Tiling for the Missing Dark Energy and VenezianoModel. Applied Mathematics, 4, 22-29. http://dx.doi.org/10.4236/am.2013.411A2005
- Sidharth, B.G. (2006) Strings and Planck Oscillator. Chaos, Solitons & Fractals, 30, 300-311. http://dx.doi.org/10.1016/j.chaos.2006.01.114
- El Naschie, M.S. (2014) Compactified Dimensions as Produced by Quantum Entanglement, the Four Dimensionality of Einstein’s Smooth Spacetime and ‘t Hooft’s 4-ε Fractal Spacetime. American Journal of Astronomy & Astrophysics, 2, 34-37. http://dx.doi.org/10.11648/j.ajaa.20140203.12
- El Naschie, M.S. (2013) Dark Energy of the Quantum Hawking-Hartle Wave of the Cosmos from the Holographic Boundary and Lie Symmetry Groups―Exact Computation and Physical Interpretation. Fractal Spacetime and Noncommutative Geometry in Quantum High Energy Physics, 3, 11-20.
- Jurkiewicz, A.J. and Loll, R. (2008) The Self-Organizing Quantum Universe. Scientific American, 24-31.
- El Naschie, M.S. (2013) A Rindler-KAM Spacetime Geometry and Scaling the Planck Scale Solves Quantum Relativity and Explains Dark Energy. International Journal of Astronomy and Astrophysics, 3, 483-493. http://dx.doi.org/10.4236/ijaa.2013.34056
- Supernova Cosmology Project Collaboration, Perlmutter, S., Aldering, G., Goldhaber, G., Knop, R.A., Nugent, P., Castro, P.G., et al. (1999) Measurements of Omega and Lambda from 42 High-Redshift Supernova. Astrophysical Journal, 517, 565-585.
- Panek, R. (2010) Dark Energy: The Biggest Mystery in the Universe. The Smithsonian Magazine. http://www.smithsonianmagazine.com/science-nature/Dark-Energy-April.
- El Naschie, M.S. (2014) On a New Elementary Particle from the Disintegration of the Symplectic’t Hooft-Veltman- Wilson Fractal Spacetime. World Journal of Nuclear Science and Technology, 4, 216-221. http://dx.doi.org/10.4236/wjnst.2014.44027
- El Naschie, M.S. (2014) Material Einstein Space-Time Produces Accelerated Cosmic Expansion. International Journal of Astronomy and Astrophysics, 4, 80-90. http://dx.doi.org/10.4236/ijaa.2014.41009
- Helal, M.A., Marek-Crnjac, L. and He, J-H. (2013) The Three Page Guide to the Most Important Results of M.S. El Naschie’s Research in E-Infinity Quantum Physics and Cosmology. Open Journal of Microphysics, 3, 141-145. http://dx.doi.org/10.4236/ojm.2013.34020
- Marek-Crnjac, L. and He, J-H. (2013) An Invitation to El Naschie’s Theory of Cantorian Space-Time and Dark Energy. International Journal of Astronomy and Astrophysics, 3, 464-471. http://dx.doi.org/10.4236/ijaa.2013.34053
- Auffray, J.P. (2014) E-Infinity Dualities, Discontinuous Spacetimes, Xonic Quantum Physics and the Decisive Experiment. Journal of Modern Physics, 5, 1427-1436. http://dx.doi.org/10.4236/jmp.2014.515144
- El Naschie, M.S. (2011) Quantum Entanglement as a Consequence of a Cantorian Micro Spacetime Geometry. Journal of Quantum Information Science, 1, 50-53. http://dx.doi.org/10.4236/jqis.2011.12007
- Amendola, L. and Tsujikawa, S. (2010) Dark Energy: Theory and Observations. Cambridge University Press, Cambridge.
- El Naschie, M.S. (2013) A Resolution of Cosmic Dark Energy via a Quantum Entanglement Relativity Theory. Journal of Quantum Information Science, 3, 23-26. http://dx.doi.org/10.4236/jqis.2013.31006
- El Naschie, M.S. (2006) Elementary Prerequisites for E-Infinity (Recommended Background Readings in Nonlinear Dynamics, Geometry and Topology). Chaos, Solitons & Fractals, 30, 579-605. http://dx.doi.org/10.1016/j.chaos.2006.03.030
- El Naschie, M.S. (2008) Extended Renormalizations Group Analysis for Quantum Gravity and Newton’s Gravitational Constant. Chaos, Solitons & Fractals, 35, 425-431. http://dx.doi.org/10.1016/j.chaos.2007.07.059
- El Naschie, M.S. (2008) Transfinite Harmonization by Taking the Dissonance out of the Quantum Field Symphony. Chaos, Solitons & Fractals, 36, 781-786. http://dx.doi.org/10.1016/j.chaos.2007.09.018
- El Naschie, M.S. (2004) A Review of E-Infinity and the Mass Spectrum of High Energy Particle Physics. Chaos, Solitons & Fractals, 19, 209-236. http://dx.doi.org/10.1016/S0960-0779(03)00278-9
- El Naschie, M.S. (2006) Elementary Number Theory in Superstring Loop Quantum Mechanics, Twistors and E-Infi- nity High Energy Physics. Chaos, Solitons & Fractals, 27, 297-330. http://dx.doi.org/10.1016/j.chaos.2005.04.116
- El Naschie, M.S. (2006) Intermediate Prerequisites for E-Infinity Theory. Chaos, Solitons & Fractals, 30, 622-628. http://dx.doi.org/10.1016/j.chaos.2006.04.042
- El Naschie, M.S. (2006) Advanced Prerequisites for E-Infinity Theory. Chaos, Solitons & Fractals, 30, 636-641. http://dx.doi.org/10.1016/j.chaos.2006.04.044
- El Naschie, M.S. (2006) Topics in the Mathematical Physics of E-Infinity Theory. Chaos, Solitons & Fractals, 30, 656-663. http://dx.doi.org/10.1016/j.chaos.2006.04.043
- El Naschie, M.S. (2009) The Theory of Cantorian Spacetime and High Energy Particle Physics (an Informal Review). Chaos, Solitons & Fractals, 41, 2635-2646. http://dx.doi.org/10.1016/j.chaos.2008.09.059
- El Naschie, M.S., Olsen, S, He, J-H., Marek-Crnjac, L., Nada, S.I. and Helal, M.A. (2012) On the Need for Fractal Logic in High Energy Quantum Physics. Fractal Spacetime & Noncommutative Geometry in Quantum & High Energy Physics, 2, 80-92.
- El Naschie, M.S. (2013) The Hyperbolic Extension of Sigalotti-Hendi-Sharifzadeh’s Golden Triangle of Special Theory of Relativity and the Nature of Dark Energy. Journal of Modern Physics, 4, 354-356. http://dx.doi.org/10.4236/jmp.2013.43049
- Connes, A. (1994) Noncommutative Geometry. Academic Press, San Diego.
- El Naschie, M.S. (2008) From Classical Gauge Theory Back to Weyl Scaling via E-Infinity Spacetime. Chaos, Solitons & Fractals, 38, 980-985. http://dx.doi.org/10.1016/j.chaos.2008.05.017
- Marek-Crnjac, L. (2003) The Mass Spectrum of High Energy Elementary Particles via El Naschie’s E-Infinity Golden Mean Nested Oscillators and the Dunkerly Southwell Eigenvalue Theorems and KAM. Chaos, Solitons & Fractals, 18, 125-133. http://dx.doi.org/10.1016/S0960-0779(02)00587-8
- Penrose, R. (2004) The Road to Reality. Jonathan Cape, London.
- He, J-H. (2005) Transfinite Physics. China Culture & Science Publishing, Beijing.
- ‘t Hooft, G. (1997) In Search of the Ultimate Building Blocks. Cambridge University Press, Cambridge.
- Wikipedia-Matter (2014) Pie Charts Showing the Fractions of Energy in the Universe. Contributed by Different Sources. http://en.wikipedia.org/wiki/Matter
- El Naschie, M.S., He, J-H., Nada, S.I., Marek-Crnjac, L. and Helal, M. (2012) Golden Mean Computer for High Energy Physics. Fractal Spacetime and Noncommutative Geometry in Quantum and High Energy Physics, 2, 80-92.
- Beck, G, Bethe, H. and Riezler, W. (1931) Remarks on Quantum Theory of the Absolute Zero Temperature. Die Naturwissenschaften, 2, 38-39. (In German)
- El Naschie, M.S. (2006) The Unreasonable Effectiveness of the Electron-Volt Units System in High Energy Physics and the Role Played by
. International Journal of Nonlinear Sciences and Numerical Simulation, 7, 119-128. http://dx.doi.org/10.1515/IJNSNS.2006.7.2.119
- El Naschie, M.S. (2006) On the Vital Role Played by the Electron-Volts Units System in High Energy Physics and Mach’s Principle of “Denkökonomie”. Chaos, Solitons & Fractals, 28, 1366-1371. http://dx.doi.org/10.1016/j.chaos.2005.11.001
- Zhong, T. (2009) From the Numeric of Dynamics to the Dynamics of Numeric and Visa Versa in High Energy Particle Physics. Chaos, Solitons & Fractals, 42, 1780-1783. http://dx.doi.org/10.1016/j.chaos.2009.03.079
- El Naschie, M.S. (2007) On the Topological Ground State of E-Infinity Spacetime and the Super String Connection. Chaos, Solitons & Fractals, 32, 468-470. http://dx.doi.org/10.1016/j.chaos.2006.08.011
- Devaney, R.L. (1989) Chaotic Dynamical Systems. Addison-Wesley, New York.
- Bhatia, N.P. and Egerland, W. (1988) A Refinement of Sarkovski’s Theorem. Proceedings of the American Mathematical Society, 102, 965-972.
- MacGregor, M.H. (2007) The Power of Alfa (α)-Electron Elementary Particle Generation With α-Quantized Lifetime and Masses. World Scientific, Singapore.
- Li, T. and Yorke, J. (1975) Period Three Implies Chaos. The American Mathematical Monthly, 82, 985-992. http://dx.doi.org/10.2307/2318254
- Rössler, O.E. (1998) Endophysics, World Scientific, Singapore. http://dx.doi.org/10.1142/3183
- El Naschie, M.S. (2001) On a General Theory for Quantum Gravity. In: Diebner, H., Druckrey, T. and Weibel, P., Eds., Science of the Interface, GenistaVerlag, Tübingen.
- Addison, P.S. (1997) Fractals and Chaos: An Illustrated Course. Institute of Physics, Bristol.
- El Naschie, M.S. (1991) Peano Dynamics as a Model for Turbulence and Strange Nonchaotic Behaviour. Acta Physica Polonica A, 80, 1-13.
- El Naschie, M.S. (2007) Feigenbaum Scenario for Turbulence and Cantorian E-Infinity Theory of High Energy Particle Physics. Chaos, Solitons & Fractals, 32, 911-915. http://dx.doi.org/10.1016/j.chaos.2006.08.014
- El Naschie, M.S. (2002) Determining the Temperature of Microwave Background Radiation from the Topology of Geometry of Spacetime. Chaos, Solitons & Fractals, 14, 1121-1126. http://dx.doi.org/10.1016/S0960-0779(02)00172-8
- El Naschie, M.S. (2009) On Zero Dimensional Points Curvature in the Dynamics of Cantorian-Fractal Spacetime Setting and High Energy Particle Physics. Chaos, Solitons & Fractals, 41, 2725-2732. http://dx.doi.org/10.1016/j.chaos.2008.10.001
- El Naschie, M.S. (2005) ‘t Hooft Ultimate Building Blocks and Spacetime as an Infinite Dimensional Set of Transfinite Discrete Points. Chaos, Solitons & Fractals, 25, 521-524. http://dx.doi.org/10.1016/j.chaos.2005.01.022
- Pati, A.K. and Brauenstein, S.L. (2009) Role of Entanglement in Quantum Computation. Indian Institute of Science Journal (Special Issue), 89, 295.
- Pati, A.K. (2006) Entanglement Guides Quantum Computation. In: Goswami, D., Ed., Quantum Coupling, Back Action, AIP Publication, College Park, Vol. 864, 114-126.
- Agrawal, P. and Pati, A.K. (2006) Perfect Teleportation and Superdense Coding with W-State. Physics Review A, 74, Article ID: 062320. http://dx.doi.org/10.1103/PhysRevA.74.062320


 . International Journal of Nonlinear Sciences and Numerical Simulation, 7, 119-128.
. International Journal of Nonlinear Sciences and Numerical Simulation, 7, 119-128.