Journal of Quantum Information Science
Vol.04 No.04(2014), Article ID:52443,41 pages
10.4236/jqis.2014.44021
Causality Is Logically Definable―Toward an Equilibrium-Based Computing Paradigm of Quantum Agents and Quantum Intelligence (QAQI) (Survey and Research)
Wen-Ran Zhang1, Karl E. Peace2
1Department of Computer Science, Georgia Southern University, Statesboro, USA
2Jiann-Ping Hsu College of Public Health, Georgia Southern University, Statesboro, USA
Email: wrzhang@georgiasouthern.edu, kepeace@georgiasouthern.edu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 August 2014; revised 3 December 2014; accepted 11 December 2014
ABSTRACT
A survey on agents, causality and intelligence is presented and an equilibrium-based computing paradigm of quantum agents and quantum intelligence (QAQI) is proposed. In the survey, Aristotle’s causality principle and its historical extensions by David Hume, Bertrand Russell, Lotfi Zadeh, Donald Rubin, Judea Pearl, Niels Bohr, Albert Einstein, David Bohm, and the causal set initiative are reviewed; bipolar dynamic logic (BDL) is introduced as a causal logic for bipolar inductive and deductive reasoning; bipolar quantum linear algebra (BQLA) is introduced as a causal algebra for quantum agent interaction and formation. Despite the widely held view that causality is undefinable with regularity, it is shown that equilibrium-based bipolar causality is logically definable using BDL and BQLA for causal inference in physical, social, biological, mental, and philosophical terms. This finding leads to the paradigm of QAQI where agents are modeled as quantum ensembles; intelligence is revealed as quantum intelligence. It is shown that the ensembles formation, mutation and interaction of agents can be described as direct or indirect results of quantum causality. Some fundamental laws of causation are presented for quantum agent entanglement and quantum intelligence. Applicability is illustrated; major challenges are identified in equilibrium based causal inference and quantum data mining.
Keywords:
Causality and Definability, Causal Logic, Causal Algebra, Quantum Agent, Quantum Intelligence, Quantum Non-Locality, Quantum Logic Gate, Energy-Information Conservation, Laws of Causation, CPT Symmetry, Mind-Body Unification, Growing and Aging, Quantum Biology, Quantum Data Mining

1. Introduction
Causality denotes a necessary relationship between one event called cause and another event called effect which is the direct consequence of the cause. According to Aristotle, everything that begins to exist must have a cause for its existence. From a modern science perspective, however, since everything begins to exist as a collection of quantum particles at the fundamental level, every being or agent can be deemed a quantum agent (QA); any causality can be deemed quantum causality, and any intelligence should fundamentally be quantum in nature. Thus, all types of intelligence can be categorized into a more general genre which is named quantum intelligence (QI) in this work. Essentially, all subatomic particles and biological systems are quantum agents; both biological intelligence and artificial intelligence (AI) belong to QI.
Without making clear the cause-effect relation any science is incomplete. But in more than 2300 years since Aristotle established his causality principle, all truth-based systems failed to provide logically definable causality with regularity that can reveal the fundamental cause of being and change in general logical or mathematical forms (note: regularity in this work refers to such regularity). The dilemma has been identified and reiterated by a number of legendary figures, notably, by David Hume―18th century Scottish philosopher and a founder of modern empiricism who challenged Aristotle’s causality principle and claimed that causation is empirical in nature and irreducible to pure regularity [1] -[3] , Bertrand Russell―one of the founders of analytic philosophy― who deemed the law of causality as “a relic of a bygone age” [4] , Niels Bohr―a father figure of quantum mechanics who asserted that a causal description of a quantum process cannot be attained and quantum mechanics has to content itself with particle-wave complementary descriptions [5] , and Lotfi Zadeh―founder of fuzzy logic―who bluntly asserted that “causality is undefinable” [6] (note: the authors acknowledge Lotfi Zadeh for his recognition [7] of the work [8] that leads to logically definable causality).
Despite the widely held view that causality is undefinable with regularity, it is shown in this paper that 1) equilibrium-based causality is logically definable with regularity and 2) such regularity leads to a ubiquitous computing paradigm of quantum agents and quantum intelligence (QAQI). Properties and applicability of the paradigm are assessed in causal inference; some inherent limitations and challenges are identified and discussed.
This work is organized into 6 sections. Following this introduction, Section 2 presents a survey on the notions of agents, causality, and intelligence. Section 3 introduces bipolar dynamic logic (BDL) as a causal logic and bipolar quantum linear algebra (BQLA) as a causal algebra that support equilibrium-based logically definable causality. Section 4 conceptualizes QAQI and presents causal structures and causal laws for the computing paradigm of QAQI. Section 5 identifies some major research challenges and applications. Section 6 draws a few conclusions and remarks.
2. Agents, Causality and Intelligence
2.1. Agents
Philosophically speaking, an agent is any entity that can act or exert power or influence to produce an effect. The agent concept is multifaceted which can be roughly classified into the following informal categories:
・ A most popular view of an agent is the representative view. If you hire a lawyer, the lawyer becomes your agent. In an espionage movie, the major player must be a secret agent of certain agency or sometimes a free agent.
・ If you are engaged in AI research you are aware of the concepts of intelligent agent, autonomous agent, and multiagent systems (MAS). Such agents can be intelligent software running on computers or roaming the World Wide Web (WWW) performing some user designated tasks such as online shopping. If the intelligent agents are autonomous robots, they may perform tasks in people’s home or roam their designated territories in the air, on land, or on the ocean floor.
・ If you are in physical sciences you are interested in chemical, biological, or physical agents at the molecular, genomic, particle, nanoparticle, and quantum levels. These agents are the major players of the microscopic worlds.
・ In information science, researchers are concerned with the collection, classification, manipulation, storage, retrieval and dissemination of information about certain agents, their interaction, and organization.
・ In cognitive information science researchers investigate the natural intelligence and internal information processing mechanisms of the brain as well as the processes involved in perception and cognition in humans or animals.
Despite the tremendous research efforts on agents, we still don’t know how a biological brain works exactly, how large the largest agent―the universe is, and how small the smallest agent―the most fundamental subatomic (quantum) particle―is. Without logically definable causality, we still haven’t found a unifying mathematical definition for the word “agent” that is fundamental for all beings and their interactions ( [9] , Ch 6). Even though string theory was considered “theory of everything”, it is criticized as not observable, not experimentally testable, and failed to provide falsifiable predictions [10] [11] . Therefore, we don’t know whether strings really exist or whether there is actually any smallest fundamental agent at all.
Although quantum computing has made progress, our understanding on the nature of quantum agents and quantum interaction is still very superficial. A mystery is that observations pertaining to entangled states appear to conflict with the property of general relativity that information cannot be transferred faster than the speed of light. Without a resolution to the quantum mystery, since the 1980s physicists, computer scientists, and cryptographers begin to regard quantum entanglement as a kind of non-classical resource that could be exploited, rather than an embarrassment to be explained away [12] . This resource view is interesting. It is discomforting, however, that the nature of the resource is so far unclear. If it is a physical resource like energy, the cause-effect relationship between entangled quantum systems has to be defined. If it is not similar to other physical resources, the fundamental difference has to be revealed. Without a clear picture on the cause-effect relationship, quantum entanglement remains mysterious. Even though Bell’s theorem [13] proved its validity from a probabilistic perspective, without a logical interpretation, the phenomenon does not lend itself to quantum biology and quantum intelligence. For instance, when a biological agent is regenerating or growing, the agent gains energy; when a biological agent is degenerating or aging, the agent loses energy. But, where is the information of the agent body and mind come from and where does it go in a growing and aging cycle?
Scientifically, observers and the observed are all agents. The failure of finding a unifying mathematical definition for the concept of agent is mainly due to two limitations: 1) the limited ability of observers to observe and 2) the limited observability of the observed. As a result, all the current agent definitions have so far failed to provide a basic theory of agent energy, agent interaction, and agent information that can lead to logically definable causality for the unification of social and physical sciences as well as relativity and quantum mechanics.
Just like water and air were believed basic elements of nature in different ancient civilizations of the East and the West, the modern concept of agent is also influenced by socioeconomics besides pure scientific exploration. That is understandable because all human agents need to consume water and air and all need to earn a living in a socioeconomic environment. Can scientific research on agents and agent interactions ever be free from socioeconomics? It seems to be difficult if not impossible. First, agents in socioeconomics are the major players on the Earth and scientific researchers themselves cannot escape from socioeconomics. Secondly, any scientific agent theory that is applicable in physical and life sciences can also be borrowed for socioeconomics because physical and social sciences share similar dynamics of a global dynamic equilibrium ( [9] , Ch 2).
Consequently, we have the question whether there is a unifying agent theory for both social and natural sciences. Intuitively, a dynamic equilibrium-based agent theory would be such a unifying theory applicable in physics, socioeconomics, and life sciences. The reason for this is that no being or agent including the universe itself can escape from dynamic equilibrium as we say the universe is either an equilibrium or non-equilibrium. Of course, after thousands of years, such a theory is still related to water, air, bread, and butter due to the threats of global warming and global economic recession which can be modeled as natural and social dynamics equilibria, respectively.
Then, what kind of equilibrium-based agent is the most fundamental agent? Without being able to find the smallest generic agent for a “theory of everything”, an open-world and open-ended approach seems to be the best choice. In such an approach, we don’t have to assume any smallest fundamental agent. Instead, we hypothesize the most fundamental property of all agents based on well-established observations. This approach actually follows the principle of exploratory scientific knowledge discovery ([9] , Preface).
While mainstream science is based on truth and singularity in which time starts with the so-called big bang and ends with a black hole [14] , dynamic equilibrium is based on bipolarity of input-output or negative-positive energies. However, the theory of truth and singularity is not a contradiction but a vindication of bipolarity because the bipolar property of nature’s basic forces and particles are the only properties that can survive a big bang as well as a black hole due to particle-antiparticle emission [15] [16] . Since the universe consists of particles and antiparticles, for any force to exist there must be one agent to act and another to react. Therefore, we have the notations (−q, +q) and (−f, +f) in modern physics textbooks and the continuing research efforts on equilibrium and non-equilibrium systems. While the dynamics and thermalization of classical systems have been extensively studied in the past, the corresponding quantum phenomena remain, to a large extent, uncharted territory [17] . Some fundamental questions are still overlooked. For instance,
・ Without bipolar dynamic equilibrium could we have truth?
・ Without bipolarity could we have agents, causality, singularity and intelligence?
・ Can a bipolar equilibrium-based logic lead to logically definable causality?
2.2. The Road to Causality
2.2.1. Aristotle’s Causality Principle
Aristotle’s Principle of Causality is deemed essential in all sciences. Each Aristotelian Science consists in the causal investigation of a specific world of reality. If such an investigation is successful, it results in causal knowledge; that is, knowledge of the relevant or appropriate causes for certain type of effects. The emphasis on the concept of cause explains why Aristotle developed a theory of causality which is commonly known as the doctrine of the four causes [18] :
・ The material cause: the material from which a thing has come or that which persists while it changes, as for example, the bronze of a statue.
・ The formal cause: whereby a thing’s dynamic form or static shape determines the thing’s properties and function, as a statue differs from a lump of bronze.
・ The efficient cause: the primary source of the change or rest, as a human lifts a rock.
・ The final cause: the end, that for the sake of which a thing is done, as his health is the result of doing exercise.
According to Aristotle, all the four types of causes may enter in the explanation of something. However, Aristotle made it very clear that all his predecessors merely touched upon these causes. That is to say, they did not engage in their causal investigation with a firm grasp of these four causes. They lacked a complete understanding of the range of possible causes and their systematic interrelations. Put differently and more boldly, their use of causality was not supported by an adequate theory of causality. According to Aristotle, this explains why their investigation, even when it resulted in important insights, was not entirely successful [18] .
Despite the great significance of Aristotle’s causality principle, it was only stated in words. Unlike his predecessors, Aristotle made causality a principle for all sciences. Like his predecessors, Aristotle failed to provide a formal logical formulation for the causality of being and change at a fundamental level. The reason why Aristotle could not provide such regularity has rarely been examined. It is a historical limitation with deep philosophical and logical roots. But at the most fundamental level, Aristotle’s syllogistic logic is bivalent, truth-based and static. Without carrying a shred of basic dynamic semantics, truth and falsity are inadequate for logically definable causality of being and change. Without such regularity, causal reasoning has been largely dependent on human understanding, subjective judgment, empirical knowledge or even religious beliefs. This situation led to a few modern critiques on the causality principle by philosophers and scientists alike.
2.2.2. David Hume’s Critique on Aristotle’s Causality Principle
David Hume was a strong critic of Aristotle’s philosophy of science. Among his criticisms the historically most famous is his critique on the principle of causality. According to Hume, the mind can never find the effect by examination of the supposed cause because the effect is totally different from the cause, and consequently can never be discovered in it. Hume shows that our causal inferences are not due to reasoning or any operation of the understanding (cf. [19] ). Hume establishes that, whatever assures us that a causal relation obtains, it is not reasoning concerning relations between ideas. Effects are distinct events from their causes: we can always conceive of one such event occurring and the other not. So causal reasoning can’t be a priori reasoning.
Hume claimed that causes and effects are discovered through experience when we find that particular objects are constantly conjoined with one another. Thus, according to Hume, our causal expectations aren’t formed on the basis of reason. But we do form and improve them through experience. The necessary connection upon which the principle of causality is based is not demonstrable, according to Hume, even by experience. He stated [1] : “The repetition of perfectly similar instances can never alone give rise to the original idea, different from what is to be found in any particular instance.” According to him, not even our activity and the effect of the will upon the movements of our body and our spirit can give us the impression of causality [1] : “No relationship is more inexplicable”, Hume adds, “than that which exists between the faculties of thought and the essence of matter.”
To Hume, it is necessary to give up attributing any objective value to the idea of cause. But from where comes the idea of causality which undeniably exists? According to Hume it arises from a psychological fact formed in the following manner (cf. [19] ):
・ Experience has shown that fact B has constantly followed fact A.
・ This stability, never contradicted by experience, shows indeed that the two facts, A and B, are associated with one another, so that the one evokes the other.
・ Through force of association there arises in me the trusting expectation, and hence the habit of expecting, that also in the future, and necessarily, granted fact A, fact B must follow.
・ Thus the necessary connection is not a bond which regulates reality, but is a manner of feeling on the part of the subject, a new law which the subject places in regard to his impressions.
Hume’s critique on Aristotle’s principle of causality is the first major challenge to the doctrine of science from an empiricist perspective. Hume’s reasoning concludes with the collapse of all rational understanding and leads inevitably to skepticism, uncertainty or fuzziness. Nevertheless, Hume’s view on causality has been widely accepted by the scientific community.
2.2.3. Bertrand Russell on Causality
Bertrand Russell was a well-known skeptic on ontological causation. A quote from his 1913 paper [4] reads: “The law of causality, I believe, like much that passes muster among philosophers, is a relic of a bygone age, surviving, like the monarchy, only because it is erroneously supposed to do no harm.” Russell argued that the philosopher’s concept of causation involving the law of universal determinism that every event has a cause as “otiose”. He claimed that, in modern science, the “otiose” law has been replaced by functional relations that are not necessarily deterministic. Based on this view, Russell later proposed the concepts of “causal lines” and “quasi-permanence” for causal inference in epistemic terms but not ontological terms [20] .
Russell is recognized as a founder of analytic philosophy. On one hand, he strongly rejected the continental tradition of idealism. On the other hand, while empiricists claim that knowledge comes from experience, not pure reason, analytical empiricism as Russell described differs from empiricism “by its incorporation of mathematics and its development of a powerful logical technique”. According to Russell “It is thus able, in regard to certain problems, to achieve definite answers, which have the quality of science rather than of philosophy. It has the advantage, in comparison with the philosophies of the system-builders, of being able to tackle its problems one at a time, instead of having to invent at one stroke a block theory of the whole universe. Its methods, in this respect, resemble those of science. I have no doubt that, in so far as philosophical knowledge is possible, it is by such methods that it must be sought; I have also no doubt that, by these methods, many ancient problems are completely soluble.” ( [21] , p. 834)
As an advocate of truth-based logical atomism, Russell holds that the world consists of ultimate logical “facts” (or “atoms”) that cannot be broken down any further. He once believed that his logical atomism and analytical empiricism would be able to solve all kinds of problems. This led to his rejection of logical holism and philosophical system building in the quest for causality.
After Russell, a number of philosophers and logicians pursued logical and ontological causality. Notably, David Lewis proposed a counterfactual approach [22] ; John Mackie proposed INUS conditions-insufficient but non-redundant parts of a condition which is itself unnecessary but sufficient for the occurrence of the effect [23] ; Georg Henrik Von Wright wrote on the logic and epistemology of causal relation [24] . These influential works largely followed the being-centered and truth-based analytic philosophy.
Now, in the 21st century, faced with global economy, global warming and the non-locality of quantum entanglement, modern science seems to be in urgent need for logical holism and new philosophical thinking. As American philosopher Richard Rorty (1931-2007) famously claimed ( [25] , p. 5): “Truth cannot be out there― cannot exist independently of the human mind―because sentences cannot so exist, or be out there. The world is out there, but descriptions of the world are not. Only descriptions of the world can be true or false. The world on its own―unaided by the describing activities of humans-cannot.” Evidently, it is reasonable to ponder on the questions: If “Truth cannot be out there”, is truth-based logical reasoning adequate for causal inference? Can dynamic equilibrium or non-equilibrium be out there? Would modern science ever embrace a new science philosophy? Is it possible to develop a causal system of logical holism for unifying science and philosophy?
2.2.4. Lotfi Zadeh on Causality
Extending Hume and Russell’s critiques on Aristotle’s principle of causality, Lotfi Zadeh―founder of fuzzy logic―has become the strongest critic on the principle in modern days. Zadeh plainly concluded in the title of his paper that “Causality Is Undefinable” [6] .
Zadeh wrote: “Attempts to formulate mathematically precise definitions of basic concepts such as causality, randomness, and probability, have a long history. The concept of hierarchical definability that is outlined in this project suggests that such definitions may not exist.” Zadeh observed that “In essence, definability is concerned with whether and how a concept, X, can be defined in a way that lends itself to mathematical analysis and computation. In mathematics, definability of mathematical concepts is taken for granted. But as we move farther into the age of machine intelligence and automated reasoning, the issue of definability is certain to grow in importance and visibility, raising basic questions that are not easy to resolve.”
Zadeh Continued: “To be more specific, let X be the concept of, say, a summary, and assume that I am instructing a machine to generate a summary of a given article or a book. To execute my instruction, the machine must be provided with a definition of what is meant by a summary. It is somewhat paradoxical that we have summarization programs that can summarize, albeit in a narrowly prescribed sense, without being able to formulate a general definition of summarization. The same applies to the concepts of causality, randomness, and probability. Indeed, it may be argued that these and many other basic concepts cannot be defined within the conceptual framework of classical logic and set theory.”
Zadeh presented in his paper a hierarchical approach to the definability of causality. The root of his hierarchy is undefinability which is decomposed into different types of definability at lower levels. He wrote: “In this perspective, the highest level of definability hierarchy, …, is that of undefinability or amorphicity. A canonical example of an amorphic concept is that of causality. More specifically, is it not possible to construct a general definition of causality such that given any two events A and B and the question, ‘Did A cause B?’, the question could be answered based on the definition. Equivalently, given any definition of causality, it will always be possible to construct examples to which the definition would not apply or yield counterintuitive results. In general, definitions of causality are non-operational because of infeasibility of conducting controlled experiments.”
Zadeh concluded: “The theory of hierarchical definability is not a theory in the traditional spirit. The definitions are informal and conclusions are not theorems. Nonetheless, it serves a significant purpose by raising significant questions about a basic issue―the issue of definability of concepts that lie at the center of scientific theories.”
Philosophically speaking, Zadeh’s view on causality is based on Aristotle’s “being qua being” metaphysics― the mainstream scientific tradition. He stated the fact that being-centered and truth-based causality is undefinable with regularity. But that does not rule out the definability of causality in any other way such as an equilibrium-based approach.
Actually, Zadeh’s observation that “In mathematics, definability of mathematical concepts is taken for granted” provides an important lead to logically definable causality. As pointed out by Bertrand Russell [26] , “Mathematics and logic, historically speaking, have been entirely distinct studies. Mathematics has been connected with science, logic with Greek. But both have developed in modern times: logic has become more mathematical and mathematics has become more logical. The consequence is that it has now become wholly impossible to draw a line between the two; in fact, the two are one. They differ as boy and man: logic is the youth of mathematics and mathematics is the manhood of logic.” Thus, mathematical definability may lead to logical definability of causality.
2.2.5. Probabilistic Causal Inference―Pearl vs. Rubin
Due to its practical applicability, probabilistic or statistical causal inference has become a most popular area of research and development in causal modeling. It has been applied in psychology, medicine, artificial intelligence, engineering, natural and social sciences. Two most popular rivalries in this line of research are Rubin’s causal model [27] -[29] vs. Pearl’s causal model [30] [31] .
Extending Hume and Russell’s views on causality in a different direction, Donald Rubin and Judea Pearl have significantly advanced the understanding of causality in statistics. While Pearl’s book Probabilistic Reasoning in Intelligent Systems [30] is among the single most influential works in shaping the theory and practice of knowledge-based systems in artificial intelligence, Rubin’s works have been leading in total number of citations in statistical analysis. While Pearl’s book Causality: Models, Reasoning, and Inference [31] went beyond computer science and engineering and has made a major impact on the definability of causality, Rubin’s causal model pioneered statistical assessment of cause and effect based on the conceptual framework of all potential outcomes and is widely used in the medical and social sciences.
Here we are focused on comparing logical and statistical approaches to causal modeling but not on the two competing statistical causal models. We randomly choose Pearl’s book as an example for our comparison with logical approaches. Contrary to Zadeh’s assertion that “Causality is undefinable”, Judea Pearl’s book Causality: Models, Reasoning, and Inference offers a complete axiomatic characterization―a structural causal model ( [31] , Ch 7). As Pearl described [32] : “Full Pearl calls for framing problems the way an investigator perceives nature to work, regardless of whether one can estimate the parameters involved, then, once you set your model, you mark down what you know and what you do not know, what you are sure about and what you are not sure about, and do the analysis in this space of ‘Nature models’. If it so happens that you are only sure about the structure of the graph and nothing else, then and only then, you do ‘graphs, colliders, and do operators’.”
It is evident from the above description that Pearl’s structural causal model is fundamentally a probabilistic approach to reasoning and inference. In order to effectively use the model, a user needs to mark down what he/she knows and what he/she does not know, what he/she is sure about and what he/she is not sure about. This treatment clearly follows the empirical and analytical spirit in line with David Hume and Bertrand Russell, where cause-effect relations are formed and improved through knowledge, experience and analysis but not on the basis of new logical development and philosophical system building. Furthermore, since any probabilistic certainty factor p can be deemed partial truth, the probabilistic approach is essentially truth-based. Therefore, probabilistic or statistical definability of causality, albeit very useful in causal inference, doesn’t go beyond truth-based reasoning and doesn’t attempt to answer the question: Is there a philosophically different fundamental causal logic system at the quantum level to be discovered?
2.2.6. Niels Bohr on Causality
Niels Bohr―a father figure of quantum mechanics―was the first to bring YinYang into quantum theory for his particle-wave complementarity principle. When Bohr was awarded the Order of the Elephant by the Danish government, he designed his own coat of arms which featured in the center a YinYang logo (or Taiji symbol) and the Latin motto “contraria sunt complementa” or “opposites are complementary” (Figure 1).
While Bohr’s quantum mechanics recognized particle-wave complementarity, it stopped short of identifying the essence of YinYang bipolar coexistence. It can be argued that without bipolarity any complementarity is less fundamental due to the missing direct “opposites” (Figure 2) [9] [33] . If bipolar equilibrium is the most fundamental form of equilibrium, any multidimensional model of spacetime such as string theory and superstring theory cannot be most fundamental.
In brief, action-reaction, particle-antiparticle, negative-positive energies, input and output, or the Yin and Yang of nature in general could be the most fundamental unitary opposites of all beings. Man and woman, space and time, particle and wave, truth and falsity are dualities or dichotomies but not exactly unitary bipolar opposites. This could be the reason why Bohr found causal description of a quantum process unattainable and we have to content ourselves with particle-wave complementary descriptions [5] . It could also be the fundamental reason why quantum entanglement is still widely deemed a logical mystery until today and quantum computing so far cannot lend itself as an analytical paradigm for quantum intelligence even though it has shown great potential for solving some problems with high computation complexity (note: Newtonian action and reaction are equal opposites that are extended to include non-equal opposites to account for modern discoveries such as CP (Charge-Parity) violation).
2.2.7. Albert Einstein on Causality
According to Yemima Ben-Menahem [34] , Einstein’s concept of causality is comprised of: (a) regularity; (b) locality; (c) symmetry considerations leading to conservation laws; (d) mutuality of causal interaction. It is well known that Einstein refused to accept Bohr’s interpretation on quantum mechanics for its lack of locality, regularity and causality. This led to the Einstein-Bohr debate about the nature of reality which is often called the great debate of the 20th century. Einstein once called quantum entanglement “spooky action at a distance”. Einstein, Podolsky, and Rosen challeged Bohr’s Copenhagen interpretation with the famous EPR thought

Figure 1. Bohr’s coat of arms (Creative Commons file by GJo, 3/8/2010, Source: File: Royal Coat of Arms of Denmark.svg (Collar of the Order of the Elephant) + File: yinyang.svg).

Figure 2. Fundamental and non-fundamental complementarities: (a) Fundamental; (b)-(d) Non-fundamental.
experiment (or EPR paradox) on quantum entanglement [35] . Until today in the 21st century, the great debate is still unsettled and the EPR paradox is still unresolved, the mysterious quantum entanglement still finds no logical interpretation.
Einstein struggled with logically definable causality for his whole academic life and never wavered on finding a logical foundation for physics. He asserted [36] : “Physics constitutes a logical system of thought which is in a state of evolution, whose basis (principles) cannot be distilled, as it were, from experience by an inductive method, but can only be arrived at by free invention.” He affirmed [37] : “Pure thought can grasp reality” and “Nature is the realization of the simplest conceivable mathematical ideas.” He reasserted [38] : “For the time being we have to admit that we do not possess any general theoretical basis for physics which can be regarded as its logical foundation.” He stated [39] : “Development of Western science is based on two great achievements: the invention of the formal logical system (in Euclidean geometry) by the Greek philosophers, and the discovery of the possibility to find out causal relationships by systematic experiment (during the Renaissance). In my opinion one has not to be astonished that the Chinese sages have not made those steps. The astonishing thing is that those discoveries were made at all.”
A few conclusions can be drawn from the above quotes. First, the logic Einstein used was the truth-based formal logical system originated from Euclidean geometry. Secondly, the truth-based system does not provide logically definable causality with regularity. Thirdly, the causality he relied on was empirical causality that is not a formal logical system. Fourthly, what he sought was a formal causal system for the grant unification.
Although Einstein never believed in the theory of singularity and even regarded the theory as “bizarre”, resisting the logic of his own theory right up to his death in 1955, his equations of general relativity did eventually lead to the flourish of singularity after his death following the discovery of black holes [14] . Based on singularity and partially observable truth, it is now a widely accepted theory that spacetime as well as the universe was created by a big bang and will end in one or more black holes. So far as we know, however, the big bang came from nowhere and caused by nothing; a black hole goes nowhere.
To reconcile the inconsistency between singularity and the second law of thermodynamics, Stephen Hawking proposed the remedy that a black hole should have particle and/or antiparticle emission or Hawking radiation [15] [16] . While Hawking radiation has been a hot topic of discussion in quantum theory, its far-reaching consequence has so far been overlooked. The consequence is that, when the universe ends, matter-antimatter bipolarity will miraculously survive. Therefore, singularity is not a contradiction but a vindication of YinYang bipolarity. Unfortunately, the vindication has so far been largely ignored.
It is reasonable to believe that the unknown logical foundation sought by Einstein could be the ultimate answer to the question why modern physics so far failed to find a definitive battleground for quantum causality and quantum gravity. It is also reasonable to question: What could be hidden in the mysterious thoughts of the Chinese sages? Could the universe be fundamentally bipolar? Could there be a formal YinYang bipolar causal system hidden behind the YinYang logo fond by Niels Bohr? (Figure 1)
2.2.8. David Bohm’s Causal Interpretation of Quantum Theory
Following Einstein, his onetime associate David Bohm continued the quest for the grand unification of general relativity and quantum mechanics. In his book Wholeness and the Implicate Order, Bohm proposed a cosmological order radically different from generally accepted conventions, which he expressed as a distinction between implicate and explicate order. Bohm wrote ([40] , p. xv):
“In the enfolded (or implicate) order, space and time are no longer the dominant factors determining the relationships of dependence or independence of different elements. Rather, an entirely different sort of basic connection of elements is possible, from which our ordinary notions of space and time, along with those of separately existent material particles, are abstracted as forms derived from the deeper order. These ordinary notions in fact appear in what is called the ‘explicate’ or ‘unfolded’ order, which is a special and distinguished form contained within the general totality of all the implicate orders.”
A major motivation of Bohm’s cosmological order was to resolve the incompatibility between quantum theory and relativity theory. He observed ([40] , p. xv):
“…in relativity, movement is continuous, causally determinate and well defined, while in quantum mechanics it is discontinuous, not causally determinate and not well-defined. Each theory is committed to its own notions of essentially static and fragmentary modes of existence (relativity to that of separate events connectible by signals, and quantum mechanics to a well-defined quantum state). One thus sees that a new kind of theory is needed which drops these basic commitments and at most recovers some essential features of the older theories as abstract forms derived from a deeper reality in which what prevails is unbroken wholeness.”
Evidently, Bohm believed that the new concept of cosmological order can be derived from a deeper reality in which undivided wholeness prevails. Central to the cosmological order is a hidden variable theory of quantum physics [41] . Bohm’s hidden variable theory forms a causal interpretation of quantum mechanics that contains a wave function―a function on the space of all possible configurations.
It is interesting to notice that, Bohm’s implicate and explicate cosmological order forms a pair denoted (im, ex) and (enfolding, unfolding). If the pairs could be defined as YinYang variables or predicates, Bohm’s interpretation would be essentially a YinYang approach to quantum gravity. A closer examination reveals that the first pair can be defined as a harmonic YinYang pair but it is not exactly bipolar in nature. The second pair, however, is exactly a YinYang bipolar pair like action-reaction. Evidently, YinYang are generally interpreted as the two sides of one thing but the two sides have to be bipolar interactive opposites for YinYang bipolar complementarity (Figure 2).
Bohm’s implicate and explicate cosmological order is an important theory and his interpretation of quantum mechanics is the first causal interpretation of its kind. It is reported that Bell’s theorem [42] was inspired by Bell’s discovery of Bohm’s early work [41] and his own subsequent wondering if the obvious non-locality of the theory could be removed.
Although Bell’s theorem has become central in quantum computing, it can be observed that Bohm’s causal interpretation and Bell’s theorem stopped short of providing a new set-theoretic mathematical abstraction and a different logical foundation for physics as envisaged by Einstein. It is said that Einstein initially encouraged Bohm’s effort on a causal interpretation, but later he dismissed Bohm’s causal wave function as “too cheap” ([43] , p. 341].
Since a new mathematical abstraction is imperative for a new logical foundation, the burden for logically definable causality does not have to be carried by physicists alone. The solution may come from mathematicians, logicians, and/or computer scientists alike. Therefore, we can ask the question: If Bohm’s explicate cosmologicalorder is truth-based and bivalent, could his implicate cosmological order be equilibrium-based and fundamentally bipolar?
2.2.9. Causal Sets
Causal set theory is a set theoretic approach to quantum gravity. The causal set research program was initiated by Rafael Sorkin [44] . Its founding principle is that spacetime is fundamentally discrete and that the spacetime events are related by a partial order. This partial order has the physical meaning of the causality relations between spacetime events.
The causal set program is based on a theorem by David Malament [45] which states that if there is a bijective map between two past and future distinguishing spacetimes which preserves their causal structure then the map is a conformal isomorphism. The conformal factor that is left undetermined is related to the volume of regions in the spacetime. This volume factor can be recovered by specifying a volume element for each spacetime point. The volume of a spacetime region could then be found by counting the number of points in that region. Among different approaches to quantum gravity, causal set theory specifically targets physical causality and quantum gravity [46] - [49] .
Although the causal set hypothesis is distinguished by its logical simplicity, it didn’t go beyond classical truth-based set theory and didn’t lead to a formal logical system beyond spacetime geometry. Therefore, it so far did not achieve logically definable causality with regularity.
2.3. Intelligence
The definition of intelligence is controversial. It is usually deemed a very general mental capability of autonomous agents that, among other things, involves the ability to reason, plan, solve problems, think abstractly, comprehend complex ideas, learn quickly and learn from experience. It reflects a broader and deeper capability for comprehending our surroundings [50] .
It is widely believed that individuals differ from one another in their ability to understand complex ideas, to adapt effectively to the environment, to learn from experience, to engage in various forms of reasoning, to overcome obstacles by taking thought. Although these individual differences can be substantial, they are never entirely consistent: a given person’s intellectual performance will vary on different occasions, in different domains, as judged by different criteria. Concepts of “intelligence” are attempts to clarify and organize this complex set of phenomena. Although considerable clarity has been achieved in some areas, no such conceptualization has yet answered all the important questions, and none commands universal assent. Indeed, when two dozen prominent theorists were asked to define intelligence, they gave two dozen, somewhat different, definitions [51] [52] .
Nevertheless, intelligence is traditionally classified as biological intelligence (BI), artificial intelligence (AI), and/or computational intelligence (CI). BI is most widely studied in humans but also observed in animals and plants; AI is human-like intelligence exhibited by machines and software named artificial agents; CI includes a set of nature-inspired computational methodologies focusing on artificial neural networks, evolutionary computation, and fuzzy logic. Among all the definitions none has provided a causal logic model for intelligence because causality has been deemed undefinable with regularity from the very beginning of logical reasoning.
In any case, our understanding on the nature of intelligence can be said very superficial and rudimentary. Even though test can be designed to assess a person’s IQ, basically, we don’t know how subatomic particles, energies, and information at the quantum level can form different agents at the higher levels and how agents can be adaptive and become intelligent start at the most fundamental level. Few have tried to unify intelligence of different categories at different levels.
It is expected that quantum biology will provide some basic understanding on the nature of intelligence such as how some birds are able to navigate between their nesting places in the far north and the far south by sensing Earth’s magnetic field. Without a logical basis for quantum entanglement, however, quantum biology is still in its infancy since its inception in the early 20th century [53] . Quantum computing is evidently suffering from the bottleneck―the lack of quantum causality for logically comprehensible analytical quantum intelligence (QI).
It can be argued that, since all beings or agents are formed with a set of quantum particles at the fundamental level, all agents can be modeled as quantum agents and all types of intelligence can be deemed as quantum intelligence. Thus, we can posit causality as a result of quantum agent interaction and a source of agent formation. For instance, at the fundamental level, the most basic logically definable quantum entanglement can be posited the ultimate source of causality for the being of all beings including but not limited to biologically intelligent agents. The key to QI is then the invention of a logic that can provide the basic definition for quantum causality and quantum entanglement as well as their ubiquitous effects in the observable world.
3. Causality Is Logically Definable
3.1. A Dream of 5000 Years
Although the causality principle was established by Aristotle 2300 years ago in ancient Greece, the dream for causality might have started long before then. For instance, the Chinese book Yi Jing (the Book of Change) suggests that everything has two opposites and all changes in nature are caused by the reciprocal interactions of the two sides. The two sides are the Yin and Yang of nature. It is estimated that the Book of Change is at least 5000 years old [54] . Therefore, the dream for causality can be said a dream of 5000 years.
While Aristotle’s truth-based bivalent logic has prospered through the history with glorious achievements, it is unfortunate that, with 5000 years of development, the Chinese Dao of YinYang has never reached the status of science philosophy due to its lack of a formal logical basis. It is a living proof to Einstein’s assertion that “the axiomatic basis of theoretical physics cannot be extracted from experience but must be freely invented” [37] .
Without an axiomatic basis, the Dao of YinYang left room for a variety of its interpretations. Some of them are scientific but not necessarily most fundamental such as the binary interpretation by Gottfried Leibniz [55] and the particle-wave complementarity interpretation by Niels Bohr [5] ; many are unscientific or superstitious such as various fortunetelling interpretations originated from the Book of Change itself. When French philosopher Jacques Derrida visited Shanghai in 2001 he reiterated German philosopher Hegel’s two century old assertion that China has no philosophy but thoughts. In his 2004 speech at Beijing, in an attempt to answer the Needham question, Nobel Laureate Chen Ning Yang attributed China’s failure in becoming the cradle of modern science to the Book of Change. While some Chinese scientists hailed Yang’s speech, many Chinese bloggers and Western sinologists were filled with righteous indignation and spoke out against it with excitement. But few pointed out the possibility of inventing a unique fundamental formal YinYang logic and geometry for logically definable causality.
As Einstein asserted, “Pure thought can grasp reality, as the ancients dreamed” and “nature is the realization of the simplest conceivable mathematical ideas”. Mankind should and must keep the dream of logically definable causality alive.
3.2. Bipolar Causal Sets and YinYang Bipolar Dynamic Logic
Philosophically speaking, truth-based mathematical abstraction follows Aristotle’s “being qua being” metaphysics that asserts truth as the essence of being. The laws of identity (A = A), contradiction ( ) and excluded middle (
) and excluded middle (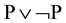 ) form the first principle of the mathematical abstraction. This principle was rarely challenged throughout history. Following the first principle, modern set theory as a mathematical foundation for computer science requires an element in a set to be self-evident and the properties of a set to be independent of the nature of its elements. This independence excludes any possibility of a formal definition for the ultimate being to reveal all beings. That is why Zadeh has to use “undefinability” to label the root of his type hierarchy [6] . It is the origin of nihilism and the source of the undefinability. After all, the identity law may not be able to hold in the quantum world. For instance, the existence of A may depend on B or A ¹ A if A and B are quantum entangled. It is well-stated by Hawking and Mlodinow ( [56] , p. 44): “Though realism may be a tempting viewpoint, ..., what we know about modern physics makes it a difficult one to defend. For example, according to the principles of quantum physics, which is an accurate description of nature, a particle has neither a definite position nor a definite velocity unless and until those quantities are measured by an observer.” They concluded: “In fact, in some cases individual objects don’t even have an independent existence but rather exist only as part of an ensemble of many.” The first principle, however, prevents truth-based mathematical abstraction from providing a dynamic causal logic system for the formations and mutations of quantum ensembles or quantum agents.
) form the first principle of the mathematical abstraction. This principle was rarely challenged throughout history. Following the first principle, modern set theory as a mathematical foundation for computer science requires an element in a set to be self-evident and the properties of a set to be independent of the nature of its elements. This independence excludes any possibility of a formal definition for the ultimate being to reveal all beings. That is why Zadeh has to use “undefinability” to label the root of his type hierarchy [6] . It is the origin of nihilism and the source of the undefinability. After all, the identity law may not be able to hold in the quantum world. For instance, the existence of A may depend on B or A ¹ A if A and B are quantum entangled. It is well-stated by Hawking and Mlodinow ( [56] , p. 44): “Though realism may be a tempting viewpoint, ..., what we know about modern physics makes it a difficult one to defend. For example, according to the principles of quantum physics, which is an accurate description of nature, a particle has neither a definite position nor a definite velocity unless and until those quantities are measured by an observer.” They concluded: “In fact, in some cases individual objects don’t even have an independent existence but rather exist only as part of an ensemble of many.” The first principle, however, prevents truth-based mathematical abstraction from providing a dynamic causal logic system for the formations and mutations of quantum ensembles or quantum agents.
While classical set theory is based on truth and singularity, bipolar set theory is based on dynamic equilibrium and bipolarity [8] [9] [57] -[61] . The equilibrium-based approach follows the ancient Chinese YinYang cosmology and asserts bipolar dynamic equilibrium (including equilibrium and quasiornon-equilibrium states) as the essence of being or agent. In this approach, a bipolar element consists of a negative pole and a positive pole. If the two poles have the same absolute values, we have a bipolar equilibrium. Otherwise, we have a non-equili- brium. Thus, bipolar sets present a major challenge to truth-based mathematical abstraction.
Ontologically, YinYang bipolarity is observable. While ether, monad, monopoles and strings are imaginable quantum agents but so far untestable, dipoles are observed everywhere; particle-antiparticle pairs (−q, +q) and action-reaction (−f, +f) are believed the most fundamental elements of the universe; negative and positive energies form the regulating force of the universe or even multiple universes ( [56] , pp. 179-180); competition and cooperation exist in any biological society; the Yin and Yang of nature is deemed a key to synthetic biology [62] ; the Yin Yang 1 (YY1) genomic regulator protein with bipolar repression-activation functions is found ubiquitous in the cells of all living species [63] -[71] ; self-negation and self-assertion bipolar emotional equilibrium or disorder is a psychiatric reality [72] [73] ; antimatter medicine is a direct use of nature’s bipolarity [74] ; it is becoming scientifically evident that brain bioelectromagnetic field is crucial for neurodynamics and different mental states [75] where bipolarity is unavoidable; bipolarity may also be holding the quantum key to the long- standing puzzle how European robins are able to navigate by sensing Earth’s magnetic field. In one word, any being or agent has to exist in certain dynamic equilibrium and bipolar dynamic equilibrium is shown to be the most basic type of equilibrium (Figure 2 and Figure 3).
With the bipolar equilibrium-based approach to mathematical abstraction, bipolar set theory leads to YinYang bipolar dynamic logic (BDL) [8] [9] [59] . In a bipolar set, elements are bipolar agents which can be entangled into an ensemble of many (Figure 3). This ontological claim positioned BDL in the context of logically definable causality for ubiquitous quantum computing and quantum intelligence.
BDL is defined on B1 = {−1, 0} × {0, +1} = {(0, 0), (0, +1), (−1, 0), (−1, +1)}―a bipolar quantum lattice in the background independent YinYang bipolar geometry ([9] , Ch 1) as shown in Figure 4. The background independent property makes quadrant irrelevant. The four values of B1 form a bipolar causal set which stand, respectively, for eternal equilibrium (0, 0), non-equilibrium (−1, 0), non-equilibrium (0, +1); equilibrium and harmony (−1, +1). Evidently, each bipolar element can be deemed a bipolar qubit that can be used to code two bits of binary information or one bit with an Ú or Ù operation on the two poles in absolute values.
Equations (1)-(12) in Table 1 provide the basic operations of BDL each of which can be a cause for an effect. The laws in Table 2 hold on BDL. Bipolar universal modus ponens (BUMP) is listed in Table 3 which formally defines equilibrium-based bipolar causality as an inference rule and leads to generic bipolar quantum entanglement. The zero order BDL has been extended to a 1st order formal system ([9] , Ch 3) in which equilibrium-based bipolar predicates can be used similarly as truth-based predicates. For instance, given bipolar agent A and let the bipolar functor (f−, f+) be self-negation and self-assertion abilities, (f−, f+) (A) can denote the mental equilibrium or non-equilibrium of A; given bipolar agents A and B and let the bipolar functor (r−, r+) be competition and cooperation relations, (r−, r+) (A, B) can denote the relation between A and B.

Figure 3. Multidimensional equilibrium or non-equilibrium deconstructed to bipolar equilibria/non-equilibria.

Figure 4. Hasse diagram of B1 in bipolar geometry.

Table 1. Yinyang bipolar dynamic logic (BDL).
Table 2. Laws of bipolar equilibrium/non-equilibrium.
Table 3. Bipolar universal modus ponens (BUMP).
Table 4. From truth-based to equilibrium-based axiomatization.
An equilibrium-based axiomatization is shown in Table 4 which has been proven sound ([9] , Ch 3). In BDL Å and Å− are “balancers” that can, at the most basic level, be used as nuclear (or mental) fusion operators; Æ, Ä, Æ− and Ä− are intuitive and counter-intuitive “oscillators” that leads to particle wave unification; & and &− are “minimizers” that can, at the most basic level, be used as particle-antiparticle annihilation operators. The linear, cross-pole, bipolar fusion, oscillation, interaction and entanglement properties are depicted in Figure 5.
Thus, BDL presents an equilibrium-based causal logic for both digital and quantum computing, where each logical operation defines a dynamic cause and each inference rule defines a cause-effect relation. While the surveyed quests in the early section for causality stopped short of going beyond classical truth-based mathematical abstraction to reach fundamental complementarity and logically definable quantum causality, bipolar causal sets and BDL as a bipolar equilibrium-based formal system presents a major step forward toward logically definable causality.
3.3. Bipolar Relations and Equilibrium Relations
As a causal set, a bipolar relational matrix is characterized with bipolar elements such as (0, 0) for no relation, (−1, 0) for conflict relation, (0, +1) for coalition, and (−1, +1) for harmonic relation, respectively. The Å-Ä bipolar transitive closure of a bipolar relation R is the smallest bipolar transitive relation containing R ([9] , Ch 3) [57] denoted by  and
 = R1 Å R2 Å R3 Å ××× (13)
It is shown that, let X = {x1, x2, ×××, xn} be a finite bipolar set, the Å−Ä bipolar transitive closure  of R in X exists, is unique, and
 = R1 Å R2 Å R3 Å ××× Å R2n. (14)
Bipolar reflexivity, symmetry and transitivity lead to the generalizations of equivalence relations to bipolar

Figure 5. Bipolar relativity: (a) Linear interaction; (b) Cross-pole non-linear interaction; (d) Oscillation; (e) Bipolar entanglement.
equilibrium relations ([9] , Ch 3) [57] and fuzzy similarity relations to bipolar fuzzy- or quasi-equilibrium relations ([9] , Ch 5) [61] . Based Equation (14), algorithms have been devised for bipolar clustering from equilibrium relations. While an equivalence relation induces partitions of equivalence sets, an equilibrium relation as a bipolar fusion or entanglement of multiple equivalence relations induces partitions of coalition sets, conflict sets, and harmonic sets ([9] , Ch 5) [61] . The partitions or clusters from an expected equilibrium state could be used as predictions for decision support [57] [58] .
3.4. Bipolar Quantum Linear Algebra
The bipolar lattice B1 = {−1, 0} × {0, +1} has been naturally extended to any integer valued bipolar lattice Bn = {−n, ×××, −2, −1, 0} × {0, +1, +2, ×××, +n} and real valued bipolar fuzzy lattice BF = [−1,0] × [0,+1] or BN = [−N, 0] × [0, +N] (9). B1 and BF are bounded and complemented unit square lattices, respectively; Bn and BN are unbounded if n, N ® ∞. "(x, y), (u, v) Î B¥ = [−∞, 0] × [0, +∞], Equation 15(a), Equation 15(b) define two algebraic operations.
Bipolar Multiplication: (x, y) × (u, v) º (xv + yu, xu + yv); (15a)
Bipolar Addition: (x, y) + (u, v) º (x + u, y + v). (15b)
In Equation 15(a), × is a cross-pole multiplication operator with the infused non-linear bipolar causal semantics −−=+, −+=+−=−, and ++=+. This operation can be deemed a generic form of quantum superposition for particle-wave and quantum-gravity unification as discussed later. In Equation 15(b), + is a linear bipolar addition or fusion operator. While linear algebra does not lend itself directly for causal reasoning and equilibrium-based computing, with the two basic operations, linear algebra is naturally extended to an equilibrium- based causal algebra named bipolar quantum linear algebra (BQLA) ([9] , Ch 8) [76] . In BQLA, bipolar matrices M1 and M2 consist of bipolar elements and their × and + operations are based on Equation 15(a), Equation 15(b).
BQLA enable bipolar fusion, fission, diffusion, interaction, oscillation, annihilation, decay, quantum superposition, quantum entanglement, generic and composite causality in a most fundamental way ([9] , Ch 7) [33] [76] [77] . Bipolar quantum entanglement enables physical or biological agents to interact through bipolar quantum fields such as bio-electromagnetic quantum fields as well as biochemical pathways in energy equilibrium or non-equilibrium. These properties also lead to the inception of YinYang bipolar atom [77] , bipolar quantum logic gates and quantum cellular combinatorics [33] . Quantum cellular combinatorics provides a modular graph theory for multidimensional bipolar cause-effect modeling (Figure 3) of YinYang-N-element cellular automata ([9] , Ch 8) [77] . Thus, BQLA enables the integration of generic bipolar agents into multidimensional bipolar agents (Figure 3, Figure 6 & Figure 7).
3.5. Like a Dream Come True
From the early sections we see that BDL can be deemed a generalization from the truth-based domain or unipolar lattice {0, 1} to the equilibrium-based domain or bipolar lattice {(0, 0) (−1, 0) (0, +1) (1, +1)}. With clear equilibrium-based semantics, BDL makes every bipolar operation a dynamic cause that leads to an effect. The validity of this generalization cannot be denied unless being or agent could escape from bipolar dynamic equilibrium and equilibrium or non-equilibrium could be ruled out from being a kind of holistic truth.

Figure 6. Matter-antimatter unification as a bipolar cellular automaton: (a) Bipolar representation of a hydrogen; (b) Bipolar representation of YinYang-n-elements; (c) Matter atom; (d) Antimatter atom; (e) Bipolar quantum cellular automaton E(t1) = M(t0) × E(t0).

Figure 7. Scalable bipolar cellular quantum automata.
From a different perspective, BDL can be deemed a logical extension from Niels Bohr’s particle-wave complementarity (Figure 1) to bipolar complementarity (Figure 2(a)) or from space-time relativity to bipolar relativity [9] . The key is BUMP which defines YinYang bipolar relativity in the form
[(f Þ j) & (y Þ c)] Þ (f*y) Þ (j*c)],
and defines bipolar quantum entanglement in the form
(fWj) Þ [(f*y)W(j*y)], where (fWj) = (fÛj) or (fWj) = (fÛ−j).
(Note: (f Û −j) Þ (f Û −f) that has anti-correlated spin case included [33] .)
Now, our general question is whether BDL will lead to logically definable causality in physical, biological, mental and social worlds. Looking at the two forms of BUMP, it looks like a dream come true.
3.6. Computational Complexity of Bipolar Causal Reasoning
Bipolar causal reasoning is achieved with a combination of (1) inductive reasoning to instantiate the bipolar universal operator * in BUMP and (2) deductive reasoning to determine the outcome. The following cascading form of BUMP can be used for the analysis of computational complexity of bipolar causal reasoning:
[(f−, f+) Þ (j-, j+)]&[(y−, y+) Þ (c−, c+)]&・・・&[(a−, a+) Þ (b−, b+)]
Þ {[(f−, f+)*1(y−, y+)*2 ・・・*i・・・* n (a−, a+)] Þ [(j−, j+)*1(c−, c+)*2・・・*i・・・*n(b−, b+)]}; (16)
where *i, i = 1 to n, is the universal operator * that can be instantiated to the same or different bipolar operators.
Theorem 1. Bipolar inductive causal reasoning with the universal operator in BUMP instantiated N times entails O(N) complexity.
Proof. Notice that each instantiation of the universal operator * requires the firing of BUMP eight times corresponding to the four pairs of dual bipolar operators &, Å, &-, Å-, Ä, Æ, Ä-, and Æ-. Since the firing of BUMP each time requires a constant number of c computational steps, the computational cost of inductive causal reasoning is determined by the number of firings. Let the number of firings be N, the total computational steps would be 8cN which result in O(N) complexity.

Theorem 2. Bipolar deductive causal reasoning entails the same computational complexity as that in classical (unipolar) logical programming except algorithms with exponential time or worse.
Proof. The complexity of bipolar logical (causal) programming in case a Prolog-like bipolar interpreter is involved with bipolar belief revision and dynamic truth maintenance seems to entail a much higher computational complexity. Surprisingly, it can be proven that bipolar deductive causal reasoning with a Prolog-like bipolar interpreter entails the same computational complexity as required for the unipolar case except algorithms with exponential time or worse. This conclusion is reached based on the following observations and analysis:
1) Each of the four linear or parallel operators {Å, &, Å-, &-} doubles the computational cost as for Ú or Ù based on the definitions of the four operations with a constant factor 2 that does not increase computational complexity except for algorithms with exponential time or worse.
2) Each of the four non-linear operators {Æ, Ä, Æ-, Ä-} requires 8 times the computational cost as for Ú or Ù based on their definitions. However, a larger constant does not increase complexity except for algorithms with exponential time or worse.
3) Each firing of a bipolar inference rule in forward and backward chaining with the bipolar implication operator Þ doubles the computational cost of firing a classical unipolar rule with the unipolar implication operator ® with a constant 2 that does not increase complexity except for algorithms with exponential time or worse.
Thus, bipolar deductive causal reasoning entails the same computational complexity as that in classical (unipolar) logical programming except algorithms with exponential time or worse.

Although the computational complexity may not increase in terms of bipolar logical programming, storage requirements will increase significantly to support bipolar belief revision and dynamic truth maintenance. This is not further discussed in this work.
4. Quantum Agents and Quantum Intelligence
4.1. Quantum Agents and Quantum Adaptivity
While previous logical systems failed to show formal dynamic semantics and logically definable causality with regularity, BDL and BQLA possess clear dynamic equilibrium-based semantics and make quantum agents, quantum causality and quantum intelligence reachable. Since everything that begins to exist must have a cause for its existence according to Aristotle, we start with a definition of being or agent.
Definition 1. An agent is any entity identifiable symbolically or mathematically. A quantum agent is a quantum particle, an ensemble of quantum particles or an ensemble of quantum agents.
By Definition 1, a quantum agent is an agent that can be physical, biological, mental, social, symbolic or mathematical. For instance, an electron e− or a positron e+ is an agent because it is an identifiable entity; the number −1 for e− or +1 for e+ is an agent if −1 or +1 is used as a mathematical identity for e− or e+, respectively. Now, we need to prove that any agent is a quantum agent.
Postulate 1. The universe and everything within the universe is a dynamic equilibrium or non-equilibrium with bipolar dynamic equilibrium or non-equilibrium of negative and positive energies as the most fundamental form.
Based on Postulate 1, we have the equilibrium-based formal definition of existence:
Definition 2a. A being or agent a exists if $j{j(a) Î B1= {−1, 0} × {0, +1} and j(a) ¹ (0, 0)}, where j is a bipolar predicate and j(a) Î B1 ensures j(a):a Þ B1 or j maps a to the bipolar quantum lattice B1.
Definition 2b. A fuzzy being or agent a exists if $j{j(a) Î BF = [−1, 0] × [0, +1] and j(a) ¹ (0, 0)}, where j is a bipolar predicate and j(a) Î BF ensures j(a):a Þ BF = [−1, 0] × [0, +1] or j maps a to the bipolar quantum lattice BF.
Definition 2c. A lattice-ordered being or agent a exists if $j{j(a) Î B∞= [−∞, 0] × [0, +∞] and j(a) ¹ (0,0)}, where j is a bipolar predicate and j(a) Î B∞ ensures j(a):a Þ B∞ or j maps a to the bipolar quantum lattice B∞.
By Definition 2, all agents are part of fuzzy agents and all fuzzy agents are part of lattice-ordered agents because B1 Ì BF Ì B∞. Since a strict bipolar quantum lattice can be normalized to the bounded and complemented bipolar lattices B1 or to BF ([9] , Ch 3, 4), without losing generality, we assume "a, j(a):a Þ B1 or j(a):a Þ BF. For algebraic analysis, however, we still need to use B∞ from time to time. For instance, let j = (−, +) be a bipolar predicate and e be an electron, positron, or a coupling (e−, e+), e exists if j(e) = (−1, 0), (0, +1), or (−1, +1); e doesn’t exist if j(e) = (0, 0). Similarly, given a person p, j(p) = (−1, 0), (0, +1), or (−1, +1) may denote the existence of p in mental depression, mania, or equilibrium, respectively. Interestingly, (−1, 0) & (0, +1) = (0, 0) characterizes an annihilation; (−1, 0) Ä (−1, 0) = (0, +1) denotes an oscillation; (−1, 0) Å (0, +1) = (−1, +1) denotes a bipolar fusion; Sp(−1, +1) = {(−1, 0) (0, +1)} characterizes a bipolar separation or fission; the total energy expansion of an atom from a finite-valued bipolar agent (x, y) toward the infinite valued bipolar agent (−∞, +∞) mathematically characterizes a nuclear fission process; the total energy degeneration of an atom from a finite-valued bipolar agent (x, y) to (−0, +0) mathematically characterizes a nuclear decay process. These semantics leads to the concept of YinYang bipolar atom [77] . The bipolar fuzzy element (−0.9 + 0.8) can characterize a quasi-equilibrium with slight “depression” and (−0.8 + 0.9) a quasi-equilibrium with slight “mania” ([9] , Ch 10).
Definition 3. A primitive agent a is a bipolar agent in a universe of discourse for which there is only a single bipolar equilibrium or non-equilibrium j such that {j(a) Î B1, BF or B∞ and j(a) ¹ (0, 0)}. Otherwise, it is non-primitive.
Following Definitions 1 - 3, we have the postulates:
Postulate 2. Any non-primitive agent in a universe of discourse is a multidimensional bipolar equilibrium or non-equilibrium with the number of dimensions N ³ 2.
Postulate 3. All agents in the universe are in either single or multidimensional bipolar dynamic equilibrium or non-equilibrium.
With Postulates 1 - 3, we can say that the universe is a multidimensional equilibrium or non-equilibrium because we have gravitational force (−f, +f), electromagnetic force (−q, +q), and particle-antiparticle (−p, +p) symmetry, quasi-symmetry or non-symmetry. With this rationale, the four dimensions of spacetime, namely, length, width, height, and time do not form YinYang bipolar equilibria and cannot lead to quantum causality or entanglement because the negative and positive sides of these dimensions namely (−x, +x), (−y, +y), (−z, +z) and (past, future) are not bipolar interactive energies. Thus, they are less fundamental concepts than YinYang bipolarity. That could be the fundamental reason why quantum entanglement is still a logical mystery and the supposedly ubiquitous effects of quantum entanglement still do not show up and make sense in spacetime geometry. And that is why a multidimensional spacetime is deemed in this paper not as fundamental as YinYang bipolar geometry. On the other hand, YinYang bipolar opposites are complementary energies. Without input information there would be no output information; without negative energy there would be no positive energy; the two opposites can form logically definable quantum causality and entanglement.
Postulates 1 - 3 open an equilibrium-based paradigm for agent interaction in logical, physical, social, mental, and biological terms. Philosophically, contrary to Aristotle’s assertion that truth is the essence of being, the three postulates assert bipolar equilibrium or non-equilibrium as the essence of any physical being or agent. Physically, the postulates claim that we humans are all bipolar in nature because we must consume energy in order to give out energy. Biologically, it is a well-known fact that our YinYang 1 (YY1) genomic regulator protein [63] regulates our gene expression with bipolar repression/activation to achieve certain genomic equilibrium or non-equilibrium. Mentally, most of us are in equilibrium with reciprocal self-negation and self-assertion abilities denoted by the bipolar predicate (self-negation, self-assertion) [72] . While some get bipolar disorder due to the loss of balance of such abilities, most of us in mental equilibrium could be either more or less “depressed” or more or less “manic” because no one has perfect self-negation and self-assertion abilities. That is why we need the concepts of fuzzy or quasi-equilibrium.
To further illustrate, let f(P) be a bipolar function and f be frequency, f(P)(f) = (−1, 0)n(3 × 1012) can denote the fact that “a quantum agent P changes polarity three trillion times per second from particle to antiparticle or vice versa”. P can be the subatomic particle named B-sub-s meson discovered at the Fermi National Accelerator Lab [78] Similarly, f(H)(f) = (−1, 0)n(k) can denote the fact that human agent H suffers from mixed bipolar disorder symptoms which switches from depression to mania k times per second. On the other hand, j(A) = (−1, +1) Ä (−1, 0) = (−1, +1) Ä (0, +1) = (−1, +1) Ä (−1, +1) can denote the fact “Agent A has strong mental equilibrium of self-negation and self-assertion abilities who can bear with negative event (−1, 0), positive event (0, +1) as well as harmonic event (−1, +1).”
Someone may argue: “If I am in bipolar mental equilibrium, how can I am bound to be true?” Actually, “I am bound to be true” really meant to be “I believe my cause is justified.” It has nothing contrary to “I am in bipolar mental equilibrium”. Evidently, anyone (good or bad) can claim having truth in his or her hand to start a contradiction, a conflict or even a world war by free will or free madness (as done by Hitler) but no one can escape from bipolar equilibrium or non-equilibrium. Actually, without bipolarity there would be no bipolar disorder, no bipolar mental equilibrium, no mind and no truth. That is why BDL satisfies the law of excluded middle and is contradiction free (Table 2).
While an electron (e−, 0) or positron (0, e+) or the coupling (e−, e+) can be deemed a primitive agent in certain cases, a person like a universe isn’t primitive because there are other bipolar equilibria involved besides (self- negation, self-assertion) such as (reaction, action). Evidently, a multidimensional equilibrium can be deconstructed into a number of bipolar equilibria (Figure 3).
Definition 4a. An agent A is bipolar adaptive if A has either self-negation ability or self-assertion ability or both and A can regain bipolar equilibrium when one of the abilities is lost temporarily. Formally, let j = (self- negation, self-assertion) Î B1 and time t = t0, t1, t2, A is adaptive if j(A) ¹ (0, 0) and A exhibits both bipolar fusion (e.g. Å) and interaction (e.g. Ä) functionalities ([9] , Ch 3).
For instance, if j(A(t0)) = (−1, 0), A exhibits self-adaptivity such that
j(A(t1)) = j(A(t0)) Å [j(A(t0)) Ä j(A(t0))] = (−1, 0) Å [(−1, 0) Ä (−1, 0)] = (−1, 0) Å (0, +1) = (−1, +1). (17)
If j(A(t0)) = (0, +1), A exhibits assisted adaptivity with external input (−1, 0) so that
j(A(t1)) = j(A(t0)) Å [j(A(t0)) Ä (−1, 0)] = (0, +1) Å [(0, +1) Ä (−1, 0)] = (0, +1) Å (−1, 0) = (−1, +1). (18)
Definition 4b. A fuzzy agent A is bipolar adaptive if A has either self-negation ability or self-assertion ability or both in any degree and A can regain bipolar equilibrium to certain degree when one of the abilities is lost temporarily. Formally, let j = (self-negation, self-assertion) Î BF and time t = t0, t1, t2, A is adaptive if j(A) ¹ (0, 0) and A exhibits both bipolar fusion and interaction functionalities ([9] , Ch 4).
For instance, if j(A(t0)) = (x, 0), −1 £ x < 0, A exhibits self-adaptivity such that
j(A(t1)) = j(A(t0)) Åij [j(A(t0)) Äijj (A(t0))] = (x, y), y > 0. (19)
If j(A(t1)) = (0, y), A exhibits assisted adaptivity with external input (−1, 0) such that
j(A(t1)) = j(A(t0)) Åij [j(A(t0)) Äijj (A(t0))] = (−|x|, y), |x| > 0. (20)
Equation (19) can be instantiated with Equation (21) in logical forms and Equation (20) can be instantiated with Equation (22) where the concepts of fuzzy or quasi-equilibrium is used (note: Åij, Äij are granular operators on real or fuzzy values ([9] , Ch 4)
j(A(t1)) = j(A(t0)) Å [j(A(t0)) Äj (A(t0))] = (−0.9, 0) Å [(−0.9, 0) Ä (−0.9, 0)]
= (−0.9, 0) Å (0, +0.81) = (−1, +0.81); (21)
j(A(t1)) = j(A(t0)) Å [j(A(t0)) Ä(−1, 0)] = (0, +0.7) Å [(0, +0.7) Ä (−1, 0)]
= (0, +0.7) Å (−0.7, 0) = (−0.7, +0.7). (22)
Equations (17) and (21) typically characterize a depressed person who may lose self-assertion ability temporarily but is self-adaptive to mental equilibrium to a certain degree because his bipolar fusion (Å) and bipolar oscillation (Ä) neurobiological functionalities are intact or working to certain degree. Thus, clinical mental depression could be diagnosed as temporary loss of bipolar fusion (Å) or bipolar interaction (Ä) functionalities. This interpretation is also supported by a Traditional Chinese Medicine principle which states Yin (−) produces Yang (+) but not vice versa.
Equations (18) and (22) typically characterize a manic person who may lose self-negation ability for a while but is able to recover to mental equilibrium to a certain degree with a medical intervention characterized with (−1, 0) such as the anti-mania medicine lithium carbonate. The recovery is possible if the patient’s bipolar fusion (Å) and bipolar interaction (Ä) functionalities responded to the medical intervention. Thus, clinical mental mania could also be diagnosed as the loss of bipolar fusion or bipolar interaction functionalities.
Definition 5a. A logical agent is an agent whose behavior is governed by Boolean logic; a bipolar agent is an agent whose behavior is governed by BDL.
Definition 5b. A fuzzy logical agent is an agent whose behavior is governed by unipolar fuzzy logic; a bipolar fuzzy agent is an agent whose behavior is governed by fuzzy BDL.
The above definitions lead to another postulate:
Postulate 4. A logical agent is not necessarily bipolar adaptive to equilibrium; a bipolar adaptive agent is not necessarily strictly logical.
Postulate 4 may sound ironic but it is actually a long overlooked observable reality. For instance, a digital computer is strictly logical but by no means adaptive to mental equilibrium even being programmed with Boolean logic because it does not have a biological mind. On the other hand, a normal person is mentally and biologically adaptive to bipolar mental equilibrium but can by no means be strictly logical like a digital computer. Another example can be taken from the quantum world where the identity law A = A in classical logic may not be able to hold because agent A may depend on agent B if the two are quantum entangled. While there is no truth-based logical definition for such entanglement, with BDL it is formulated as a causal inference rule (fWj) Þ [(f*y)W(j*y)] [33] . Thus, Postulates 1 - 4 form an axiomatic basis for agent interaction, mind and body unification, and causal axiomatization in a fundamental way.
Definition 6. Two bipolar sets X and Y are physically bipolar interactive if, "x Î X and "y Î Y, x and y can be (but does not have to be) physically bipolar interactive denoted x¨y. Two bipolar predicates j(x) Î B1 or BF and f(y) Î B1 or BF are logically bipolar interactive denoted j(x)*f(y) iff x and y are either physically bipolar interactive (x¨y ) or logically bipolar interactive (x*y).
Definition 6 establishes the physical basis for bipolar equilibrium-based logical reasoning. For instance, a set of bipolar disorder patients X and a set of bipolar disorder medicines Y can be physically bipolar interactive such that two functions j(x) and f(y) are logically bipolar interactive. On the other hand, two sets of bipolar disorder patients X and Y can’t be physically bipolar interactive and j(x) and f(y) can’t be logically bipolar interactive either in terms of medical cause and effect. Since bipolar variables or functions can form sets X and Y themselves, the recursive nature of Definition 6 is necessary such that if a = j(x) and b = f(y) the logical interactivity of a and b depends on that of j(x) and f(y). In the meantime, physical interactivity can be a default in hypothesis-driven reasoning.
The following have been proven on agent interactivities ([9] , Ch 6):
"x, y, if [(j−, j+)(x)*(f −, f+)(y)], then (x¨y)Ú(x*y);
"x, y, if x¨y, then [(f−, f+)(x)*(f −, f+)(y)] Þ (f−, f+)(x¨y);
"x, y, if x*y, then [(f−, f+)(x)*(f −, f+)(y)] Þ (f−, f+)(x*y);
"x, y Î B1 or BF,, (x¨y) º (x*y). // logical-physical equivalence
Bipolar interactions can be chemical, biological, organizational, or any other type. Physical and logical interaction with construction or deconstruction may lead to scalability. It is noteworthy to distinguish bipolar agent interactions from multiagent communications [79] -[84] . While the goal of multiagent communication is for multiagent coordination and distributed AI (DAI), the goal of bipolar agent interaction is for logically definable causality and quantum intelligence. It is interesting to notice though that bipolar cognitive mapping can be used for multiagent coordination [57] [58] [60] [61] [85] - [88] . Thus, QAQI can be deemed a causal set extension to DAI.
Causation Law 1. Bipolar adaptivity is a most fundamental form of adaptivity.
Proof. Logically, bipolar adaptivity (Equations (17), (18)) is a minimal or primitive form of adaptivity from non-equilibrium to equilibrium that cannot be further simplified. Physically, without bipolar adaptivity the universe would not be able to adapt to any equilibrium state and would be in total disorder or chaos. Mentally, without bipolar mental adaptivity it would be impossible for the human mind to reach certain mental equilibrium of self-negation and self-assertion abilities. Biologically, without bipolar adaptivity it would be impossible for a biological system to realize certain biological equilibrium of growing and aging.

Causation Law 2. Bipolar adaptivity is the most fundamental form of intelligence from which biological and artificial intelligence can be developed.
Proof. It follows the proof for Law 1 with the additional arguments: (1) artificial intelligence is based on biological intelligence; (2) any biological agent must at least adapt to certain energy input-output bipolar dynamic equilibrium, otherwise, the agent cannot exist; (3) without genomic repression-activation bipolar adaptivity of the ubiquitous Yin Yang 1 regulator protein, there would be no biological cell; (4) without self-negation and self-assertion bipolar adaptivity, an agent would have no learning ability, no mental equilibrium, no healthy genetic mutation, no mind, no truth, and no intelligence.

Causation Law 3. All agents are fundamentally quantum agents and all types of intelligence are fundamentally equilibrium-based quantum intelligence―a direct or indirect result of bipolar quantum interaction.
Proof. It follows Definitions 1 - 4, the proofs for Laws 1 - 2 and the established theory that the universe consists of particles and antiparticles, actions and reactions as well as negative and positive energies. Therefore, without negative agent there would be no positive agent and without bipolar interaction there would be no agent of any kind.

Here it should be clarified that (1) if an agent is not bipolar adaptive to equilibrium it can still be in a non-equilibrium quantum state and (2) if a bipolar adaptive agent is not strictly logical it can be in a dynamic equilibrium state. Thus, both truth-based logical and equilibrium-based logical agents can be fundamentally quantum in nature.
4.2. Laws of Causation and Ensemble Formation of Quantum Agents
Programming the Universe is a book title by MIT professor Seth Lloyd [89] . The book posits the universe itself as a giant quantum computer. According to Lloyd, the universe is all about quantum information processing. Once we understand the laws of physics completely, we will be able to use small-scale quantum computing to understand the universe completely as well. Lloyd’s idea can be deemed an extension to Einstein’s assertion: “pure thought can grasp reality, as the ancients dreamed” and “nature is the realization of the simplest conceivable mathematical ideas”.
While BDL is concerned with the logic of reciprocal interactions among individual elements modeled as bipolar equilibrium or non-equilibrium, BQLA is for mathematical modeling of agents as multidimensional bipolar equilibriums (Figure 1 and Figure 7). It provides a representational basis for characterizing matter-antimatter atoms, molecular and cellular structures as well as different social, biological and mental systems [9] [77] .
Equilibrium-Based Unification of Energy and Information. Since every being is a dynamic equilibrium, bipolar equilibrium or non-equilibrium states of input and output provide a basis for an equilibrium-based unification of energy and information. This unification makes ubiquitous quantum computing possible where faster than light speed [90] - [92] can be deemed quantum information transmission at unobservable energy levels ([9] , Ch 7). With this unification, BDL and BQLA lead to the concept of bipolar quantum gates [33] .
Given bipolar column vector E and a bipolar connectivity matrix M we have Equation (24) in a causal form based on Equations 15(a), (b), where E(t) is the energy-information vector of a quantum agent at time t; M(t) is a bipolar connectivity matrix characterizing the organization of the agent such as an atom at time t; M(t) × E(t) is a cause and E(t + 1) is the effect (Figure 6).
E(t + 1) = M(t) × E(t) (24)
Bipolar Holographic Information. While energy-information gain without bipolarity used to be a scalar variable, with bipolarity the energy of a bipolar matrix E or M provides bipolar holographic information with the dimensions of negative, positive, bipolar, and absolute total views.
For instance, given the row matrix R = [(−0.7, +0.3)(−0.3, +0.8)], we have (Zhang [57] [58] ):
Negative Energy: e−(R) = e−((−0.7) + (−0.3), (+0.3 + 0.8)) = e−(−1.0, +1.1) = −1.0;
Positive Energy: e+(R) = e+((−0.7) + (−0.3), (+0.3 + 0.8)) = e+(−1.0, +1.1) = +1.1;
Bipolar Energy: e(R) = (e−(R), e+(R)) = (−1.0, +1.1);
Absolute Total Energy: |e|(R) = |e−(R)| + |e+(R)| = 1.0 + 1.1 = 2.1.
Definition 7a. Energy-information Conservational Bipolar Quantum (Logic) Gate. If the absolute energy of each row and each column of a bipolar connectivity matrix M(t) of a quantum agent in Equation (24) adds up to |e| = 1.0, we call M(t) an energy-information conservational bipolar quantum gate at time t [33] .
Definition 7b. Energy-information Degenerating Bipolar Quantum (Logic) Gate. If the absolute energy of each row and each column of a bipolar connectivity matrix M(t) of a quantum agent in Equation (24) adds up to |e| < 1.0, we call M(t) an energy-information degenerating bipolar quantum gate at time t.
Definition 7c. Energy-information Regenerating Bipolar Quantum (Logic) Gate. If the absolute energy of each row and each column of a bipolar connectivity matrix M(t) of a quantum agent in Equation (24) adds up to |e| > 1.0, we call M(t) an energy-information regenerating bipolar quantum gate at time t.
Causation Law 4. Law of Energy-Information Conservation. If M is an energy-information conservational quantum gate at time t, the cause-effect relation E(t + 1) = M(t) × E(t) satisfies Equation (25).
|e|(E(t + 1)) = |e|(M(t) × E(t)) º |e|(E(t)). (25)
Proof. It follows that if M is energy-information conservational at time t, it enables the transmission and distribution of the energy of each element of E(t) to those in E(t + 1) in exactly 100%. While CP (charge-parity) violation may be observed, total energy-information conservation is achieved.

For instance, given


M is energy-information conservational because
Energy of Row1 = (|e|(−0.3, 0.2) + |e|(−0.5, 0.0)) = |−0.3| + 0.2 + |−0.5| + 0.0 = 1.0;
Energy of Row2 = (|e|(−0.4, 0.1) + |e|(0.0, 0.5)) = |−0.4| + 0.1 + |0.0| + 0.5 = 1.0;
Energy of Column1 = (|e|(−0.3, 0.2) + |e|(−0.4, 0.1)) = |−0.3| + 0.2 + |−0.4| + 0.1 = 1.0;
Energy of Column2 = (|e|(−0.5, 0.0) + |e|(0.0, 0.5)) = |−0.5| + 0.0 + |0.0| + 0.5 = 1.0;
Based on Equations 15(a), (b), we have the following BQLA matrix operation:

|e|E(t1) = |e|(M(t0) × E(t0)) =

Causation Law 5. Law of Energy-information Degeneration. If M is an energy-information degenerating quantum gate at time t, E(t + 1) = M(t) × E(t) satisfies Equation (26) and characterizes the weakening of a quantum agent (such as nuclear decay or biological aging).
|e|(E(t + 1)) = |e|(M(t) × E(t)) < |e|(E(t)). (26)
Proof. It follows that if M is energy-information degenerating at time t, it enables the transmission and distribution of the energy of each element of E(t) to those in E(t + 1) in less than 100%.

Causation Law 6. Law of Energy-information Regeneration. If M is an energy-information regenerating bipolar quantum gate at time t, E(t + 1) = M(t) × E(t) satisfies Equation (27) and characterizes the strengthening of a quantum agent (such as nuclear fission and biological growing).
|e|(E(t + 1)) = |e|(M(t) × E(t)) > |e|(E(t)) (27)
Proof. It follows that if M is energy-information regenerating at time t, it enables the transmission and distribution of the energy of each element of E(t) to those in E(t + 1) in more than 100%.

Evidently, BDL, BQLA and bipolar quantum logic gates could be a key step toward definable causality. Such definability should show regularity that lends itself to logical analysis and computation for both generic and composite cause-effect relations.
The Role of Bipolarity. Without bipolarity, classical linear algebra is incapable of holistic bipolar causal interaction and coordination for normal energy-information conservation, degeneration and regeneration due to bipolar cancelation. For instance,

Of course, we can use a positive quantum gate matrix for energy-information conservation, a positive matrix, however, does not show bipolar regulation or balancing cause-effect toward bipolar equilibrium. For instance,

Bipolar Generalization of Unitary Quantum (Logic) Gates. While quantum computing has made progress, without logically definable quantum causality the ubiquitous effect of quantum entanglement has so far remained a mystery ([93] , p. 591), the intrinsic relationships between quantum logic circuitry and bio-cellular networks has been unknown, and quantum intelligence has been an untouched subject. Energy-information conservational, degenerating and regenerating bipolar quantum gates provide a bipolar generalization of unitary quantum gates. Evidently, any integer unitary quantum logic gate (matrix) in quantum computing must be energy-information conservational. Therefore, unitary quantum gate can be deemed part of energy-information conservation. With the bipolar decimal generalization, unitarity and reversibility in quantum computing [94] [95] are successfully generalized to the thermodynamic causal laws of energy-information conservation and non-con- servation for regulating or governing agents’ body, mind, and/or behaviors. This illustrates the quantum nature of all agents and provides a basis for equilibrium-based ubiquitous quantum computing and quantum intelligence. Here, the distinguishing factor is bipolarity which makes agent regulation possible by the negative-positive energies of bipolar quantum gates. Moreover, local regulating energies can be further regulated by a global dynamic equilibrium process. For instance, biological agents can be affected by global warming. Remarkably, a degree of nature-man unity is logically reached for computational equilibrium and harmony.
While the decimal extension to bipolar quantum gate leads to quantum cellular combinatorics for QAQI [33] , bipolar coding does not exclude binary coding with probability coefficients. For instance, the bipolar values in B1 (Figure 3) can be used to create a macroscopically coherent bipolar superposition in the form c00|(0, 0)〉 + c01|(0, 1)〉 + c10|(−1, 0)〉 + c11|(−1, +1)〉 [33] . The bipolar superposition can be matched to c00|00〉 + c01|01〉 + c10|10〉 + c11|11〉 of a traditional 2-qubit system. While the traditional basis states use binary bit patterns without quantum causality and basis state entanglement, the bipolar basis states are logical values in BDL that form a bipolar causal set and can lead to basis state quantum entanglement.
Organizational Energy or Information of Nature-Agent Unity. The energy of the connectivity matrix M (or bipolar quantum gate) can be deemed the organizational energy or information at the regulating center of a quantum agent that assembles a set of bipolar elements in E into an ensemble quantum entanglement. This entanglement makes it possible to model an agent as a nonlinear dynamic quantum process of local equilibrium or non-equilibrium as part of the global equilibrium or non-equilibrium with nature-agent unity―a key step toward nature-man harmony. A most common but so far overlooked bipolar regulating center is the nucleus of an atom or antiatom, where quarks in different flavors of particle or antiparticle pairs assemble negatively and positively charged electrons or positrons into matter or antimatter (Figure 6). Another example is in biology, where a young biological system can grow with input energy but an old one may have to degenerate anyway. For instance, in the process of photosynthesis [53] “Particles of light called photons, streaming down from the Sun, arrive randomly at the chlorophyll molecules and other light-absorbing ‘antenna’ pigments that cluster inside the cells of every leaf, and within every photosynthetic bacterium. But once the photons’ energy is deposited, it doesn’t stay random. Somehow, it gets channelled into a steady flow towards the cell’s photosynthetic reaction centre, which can then use it at maximum efficiency to convert carbon dioxide into sugars.” In such a way, tree leaves can grow and become greener in Spring and Summer, however, the maximum efficiency eventually fades away and they may have to change color from green to yellow in the Fall.
Matter-Antimatter Unification. Since both matter and antimatter atoms can be characterized as a multidimensional bipolar dynamic equilibrium, matter and antimatter atoms can be unified as a bipolar cellular automaton with a single BQLA equation of negative-positive energies for equilibrium and non-equilibrium analysis (see Equations (24)-(27) and Figure 6). The matter-antimatter quantum agent unification is made possible by the background independent property of YinYang bipolar geometry. The property accounts for both the negative and positive sides but transcends spacetime and makes quadrants irrelevant.
Particle-Wave Unification. Regardless of the global energy-information conservational or non-conservational properties of a quantum agent, each elementary bipolar agent can have different local bipolar energy wave forms [77] . Thus, particle-wave unification is made achievable by (1) identifying bipolarity as the most fundamental complementarity―an extension to Bohr’s particle-wave complementarity principle [5] , and (2) identifying negative-positive energies or the Yin and the Yang as the regulating power of all agents in the universe including the universe itself―an extension to The Grand Design ([56] , pp. 179-180). While particle-wave complementarity without bipolarity is less fundamental due to the lack of direct “opposites” (Figure 2), particles and waves are unified as causal sets or ensembles of bipolar elements with bipolarity (Table 5; Figures 6-8). Remarkably, the wave forms are generated with object orientated programming that provides another proof for the unification.
Scalability of Quantum Agents. Since the equilibrium or non-equilibrium states of any quantum agent such as atom, molecule, cell, human brain or the universe can be modeled as a quantum cellular automaton [9] , the bipolar atom model in Figure 6 provides a scalable building block―a bio-economics or quantum-economics model for what exist in dynamic equilibrium and harmony. For instance, the cellular automaton in Figure 6 can become a bipolar element in Figure 7.
Algorithms have been developed for the simulation of a bipolar cellular automaton as a dynamic equilibrium with energy-information conservation, degenerating and regenerating as well as oscillation states (Table 5; Figures 6-8). Interestingly, bipolar random variables are involved in the computation. That is, the connectivity
Table 5. C++ algorithms for testing energy-information equilibrium [76] .


Figure 8. (a) Bipolar energy rebalancing to equilibrium after a disturbance to one of many elements; (b) Elementary bipolar energy increase (or fission) under non-equilibrium condition; (c) Elementary bipolar energy decrease (or decay) under non-equilibrium condition; (d) Elementary bipolar energy oscillation under global energy conservation.
matrix or quantum gate M in Figure 6 or Figure 7 may have bipolar random connectivity which suggests a new theory of bipolar eqilibrium-based quantum probability. Empirical knowledge and learning algorithms can be used in bipolar causal inference to achieve equilibrium and harmony for multiagent coordination and DAI. This is not covered in this work.
Definition 8. Given two quantum agents A1 and A2 in either primitive (logical) or composite (matrix) form, we say A1 and A2 are in a 2-party quantum entanglement, denoted A1WA2, if A1 Û A2 or A1 Û −A2, where the bipolar equivalence operator Û is generalized from its logical equivalence (Table 1) to matrix equivalence. Formally, we have
{A1 Û A2} Þ {"i, j, A1[i, j] Û A2[i, j]}; {A1 Û −A2} Þ {"i, j, A1[i, j] Û −A2[i, j]};
{A1WA2} Þ{A1 Û A2} or {A1WA2} Þ {A1 Û −A2}.
It should be noted that, for any bipolar agent A we have |e|A º |e|(−A). Thus, the negation operation (−) is energy-information conservational. On the other hand, since |e|(0, 0) ¹ |e|(Ø(0, 0)) = |e|(−1, +1), the complement operation (Ø) is not energy-information conservational in general, even though it can be in certain symmetrical cases [33] .
Causation Law 7. Law of 2-Party Quantum Agent Entanglement. Given two bipolar agents A1(t + 1) = E1(t + 1) = M1(t) × E1(t) and A2(t + 1) = E2(t + 1) = M2(t) × E2(t), a necessary condition to keep the two agents in a 2-party entanglement is to keep M1(t)[i, j] and M2(t)[i, j] identical in both energy and parity at all times for all i and j. Formally,
"t, i, j, (A1(t + 1)WA2(t + 1)) ® (M1(t)[i, j] Û M2(t)[i, j]). (28)
Proof. To have A1(t + 1)WA2(t + 1), we have either E1(t) Û E2(t) or E1(t) Û −E2(t). If the corresponding elements M1(t)[i, j] and M2(t)[i, j] are not identical in both energy and parity at any time and for all i and j, the equivalence condition E1(t + 1) Û E2(t + 1) or E1(t + 1) Û −E2(t + 1) will be violated and there would be no 2-party entanglement.

It should be remarked that Law 7 provides a necessary condition that may not be sufficient. For instance, A1WA2 may also implies that M1 and M2 be energy-information conservational or unitary. Otherwise, the entanglement may collapse.
Causation Law 8. Equilibrium-Based Unification of Quantum Agents and Quantum Entanglement. Two entangled quantum agents A1 and A2 can be mathematically described as two elements of one agent or a bipolar causal set A = {A1, A2} that share the same reality characterized by a bipolar quantum gate matrix M1 º M2. Thus, quantum teleportation through quantum entanglement can be either interpreted as instant change of an entangled state in a geometry that transcends spacetime or interpreted as sending information much faster than the speed of light in spacetime geometry. The two interpretations are essentially two views of one reality.
Proof. (1) If A1 W A2, they must have shared a common history of being two aspects of one bipolar agent A = {A1, A2}; (2) The space separation of A1 and A2 doesn’t change their status of being two aspects of one agent― in an equilibrium-based entanglement; (3) Quantum entanglement can be logically defined in the background independent YinYang bipolar geometry with spacetime transcendence (Figure 3, Figure 4, Figure 10); (4) Faster than light speed of quantum entanglement has been observed, questioned, and reconfirmed in spacetime geometry [90] -[92] ; (5) If the two quantum gate matrices M1 and M2 were not for the same reality, it would be impossible to satisfy Equation (28).

Unification of Quantum Locality and Non-Locality. Quantum entanglement or quantum non-locality as an unresolved logical paradox has generated enormous amount of confusion. It was once called “spooky action at a distance” by Einstein. Law 8 provides an equilibrium-based agent-oriented holistic resolution to the paradox. From Law 8, the following can be conjectured:
Conjecture 1. Quantum entanglement can be classified as local and non-local.
Conjecture 2. Matter or anti-matter atom is a set of n-party locally entangled electron-positron pairs through a bipolar quantum gate characterizing the organization of the atom (Figure 6).
Conjecture 3. An agent with multiple atoms can be deemed an entangled set of n-party local entanglements.
Conjecture 4. The universe is a combination of local and non-local entanglements.
The unification of quantum locality and non-locality provides a basis for quantum biology, mind-body unification and quantum intelligence. Evidently, a background independent geometry with space-time transcendence is essential for logically definable quantum causality as well as local and non-local quantum entanglements.
Causation Law 9. Equilibrium Law of Collective Adaptation to Super Symmetry. Given E(t + 1) = M(t) × E(t) with the two conditions of (1) "t, M(t) is energy-information conservational and (2) "t, the absolute values of the negative and positive energies of each row and each column of M are both greater than 0.0, without external disturbance, all bipolar elements in E connected by M will eventually reach a YinYang bipolar symmetry (−|ε|E/(2K), |ε|E/(2K)) at certain time t, where |ε|E is the total energy of E and K is the number of bipolar elements in E.
Proof. It follows that Condition (1) enables the energy of each element of E(t) be transmitted and distributed to E(t + 1) in 100% with or without CP violation; Condition (2) prevents the energy of E from bipolar oscillation. Thus, the rebalancing process will continue based on Equations 15(a), (b) until bipolar equilibrium or symmetry is reached.

Generalized CPT Super Symmetry. With the discovery of CP violation, CPT (Charge-Parity-Time) symmetry is now believed a fundamental law in physics [96] , which explains why the universe exists as it is. But the cause of this law has been a mystery. The supper symmetry in the above law can be deemed an equilibrium- based causation law of generalized CPT (G-CPT) for super symmetry. In G-CPT symmetry, particle-antiparticle and gravitational action-reaction are logically unified into a superposition for a S5 paradigm of logical, physical, social, biological and mental quantum gravities [9] [77] . This is made possible by the basic BDL and BQLA operations and by the background independent YinYang bipolar geometry (Figure 4, Figure 10).
Corollary of Law 9. Bipolarity is not an option but a necessity and fundamental property of nature for equilibrium-based regulation and quantum agent self-adaptation to bipolar equilibrium, symmetry and harmony in logical, physical, social, biological and mental terms.
Proof. First, without bipolarity, there would be no charge parity. Secondly, without bipolarity, condition (2) in Law 9 cannot be met and there would be no CPT symmetry. Thirdly, without bipolarity, there would be no dynamic equilibrium, no order, no harmony, no mind, no truth, no agent, and no universe.

Table 6 shows a simulated example of bipolar equilibrium-based rebalancing to G-CPT symmetry. Figure 9 shows the wave forms of each element in the process. Evidently, without bipolarity, classical linear algebra is inadequate for characterizing bipolar interactions.
4.3. Toward Quantum Intelligence
BDL and BQLA provide a mathematical basis for a ubiquitous computing paradigm of quantum agents and quantum intelligence (QAQI) with a number of distinguishing features which are analyzed in this section.
4.3.1. Bipolar Geometry Transcends Spacetime
Bipolar sets and BDL are defined in YinYang bipolar geometry which transcends spacetime [97] with complete background-independence [98] . In the new geometry quadrant is irrelevant; space and time can be emerging factors (Figure 10 and Equation (23)); equilibrium-based bipolar causal sets and BDL can be hosted and used for logical reasoning and quantum computing. While background-independence has been desirable but rarely
Table 6. Simulation of bipolar equilibrium-based rebalancing to symmetry.

Figure 9. Simulation of bipolar equilibrium-based rebalancing to symmetry.
achievable in the quest for quantum gravity in physics, it is achieved with YinYang bipolar geometry―so far the only known background independent geometry that leads to logically definable causality with regularity. With the new geometry, bipolar quantum entanglement can be logically defined; space and time can be the result of quantum agent interaction; emotional intelligence can be included in the general category of quantum intelligence. These have not been possible in spacetime geometry such as in string theory or in any other known background independent geometry such as loop quantum gravity. Philosophically, with the new geometry, being and truth including space and time themselves are freed from the physical limitations of spacetime. Scientifically,

Figure 10. A generic version of background-independent yinyang bipolar geometry: (a) Magnitudes of Yin and Yang; (b) Growing curve; (c) Quadrant irrelevant property.
new discoveries are made possible with the freedom. For instance, the long desired space and time can emerge from the new geometry as a result of particle-antiparticle interaction.
Defined in YinYang bipolar geometry, BDL unified truth, equilibrium, causality and quantum entanglement. In this unification, bipolar quantum entanglement―a truth-based paradox in spacetime becomes a sound new law in the new geometry. A key element in the unification is BUMP that leads to YinYang bipolar relativity and quantum entanglement of negative-positive energies, formally, "a, b, c, d, we have
[(y(a(tx, p1)) Þ c(c(ty, p3))) & (f(b(tx, p2)) Þ j(d(ty, p4)))]
Þ [(y(a(tx, p1))*f(b(tx, p2))) Þ (c(c(ty, p3))*j(d(ty, p4)))]. (29)
In Equation (29), a(tx, p1), b(ty, p2), c(tx, p3), d(ty, p4) are any bipolar agents where a(t, p) stands for “agent a at time t and space p” (tx, ty, px and py can be the same or different points in time and space). An agent without time and space is assumed at all time and space p. An agent at time t and space p is therefore more specific. The geometry in Figure 10 can be deemed a generic bipolar geometry which can be integrated into a multidimensional equilibrium using BQLA (see Figure 3, Figure 6, Figure 7).
4.3.2. BDL Is Computational
Classical 1st order logic or Boolean logic is derivable from BDL but not vice versa ([9] , Ch 3) [59] . This can be observed from the equilibrium-based axiomatization in Table 4. In this table all rules except BUMP can be seen linearly equivalent to their truth-based counterparts and MP can be derived from BUMP but not vice versa ([9] , Ch 3). This observation qualifies BDL as a non-linear bipolar dynamic generalization of 1st order logic from truth-based to equilibrium-based domain. Despite the non-linearity, BDL satisfies the law of excluded middle and is contradiction-free (Table 2). In addition it has led to the generalizations of equivalence relation to equilibrium relation, fuzzy sets to bipolar fuzzy sets, fuzzy similarity relation to quasi-equilibrium relation, and linear algebra to bipolar quantum linear algebra [9] . Thus, BDL is equilibrium-based logical and computational.
4.3.3. BDL Leads to Logically Definable Causality
Since classical modus ponens (MP) can be derived from bipolar universal modus ponens (BUMP) but not vice versa ([9] , Ch 3), BUMP is qualified to be an equilibrium-based generalization of MP from spacetime geometry to YinYang bipolar geometry. Since for all bipolar equilibrium functions f, j, y, c, if (f Þ j) and (y Þ c), we must have (f*y) Þ (j*c), BUMP formally defines fundamental, non-linear dynamic, and logically definable equilibrium-based causality with regularity for the first time ever (Table 3, Table 4). On the other hand since equilibrium or non-equilibrium of any agent is a fundamental concept in both the quantum world and the biological world, bipolar causality provides a logical basis for quantum entanglement and quantum intelligence.
Why unipolar truth-based modus ponens (MP) in the form “A®B, A then B” cannot provide logically definable causality with regularity? This is an interesting question that has been without an answer for thousands of years. Compared with BUMP, it is evident that truth variables in MP are static but causality needs dynamic semantics such as bipolar fusion, fission, annihilation, and oscillation for equilibrium, non-equilibrium or quasi-equilibrium. For instance, using MP false®true is true and true®true is also true; it is impossible to have dynamic operations with formal cause-effect relations for bipolar agent interaction such as
・ Fusion: (0, +1) Å (−1, 0) = (−1, +1);
・ Separation: Sp(−1, +1) = {(−1, 0)(0, +1)};
・ Annihilation: (0, +1) & (−1, 0) = (0, 0);
・ Oscillation: (−1, 0) Ä (−1, 0) = (0, +1);
・ Fission: Sp(−∞, +∞) = {(−∞, +0) (−0, +∞)}.
Why cannot the other families of multivalued logic [99] , fuzzy logic [100] , intuitionistic logic [101] , paraconsistent logic [102] , and quantum logic [103] provide logically definable causality with regularity? This is another interesting question that has been without an answer for many decades. Among different reasons, a fundamental one is that all these logical systems are static truth-based extensions to classical logic that bear no bipolar equilibrium-based dynamic semantics. But any being or agent including the universe itself must be in certain bipolar equilibrium or non-equilibrium.
4.3.4. BDL Leads to the Unification of Physical and Social Quantum Relativity
BUMP logically (not quantitatively) defines quantum relativity with bipolar variables of action-reaction in the physical world or competition-cooperation in the social world [9] . It can be stated that, for all bipolar variables or functions f, j, y, and c, IF (f Þ j)&(y Þ c), THEN the bipolar interaction (f*y) implies that of (j*c) or formally expressed as (f*y) Þ (j*c).
4.3.5. BDL Leads to the Unification of Logical, Physical, Social, Biological, and Mental Quantum Entanglement
BUMP makes bipolar quantum entanglement logically definable with YinYang bipolar variables (Table 4). It can be stated as, for all bipolar equilibrium functions f, j, y, IF (fWj), THEN we must have (f*y) Û (j*y). Since this quantum entanglement is equilibrium-based and ubiquitous, it can be logical, physical, social, biological, or mental; and it provides a basis for mind-body unification (see Law 8).
4.3.6. BDL Is Simple and Meaningful
BDL is simple and meaningful. While it is significantly more complex than Boolean logic at the elementary level, it is much simpler than string theory and M-theory. Unlike string theory, which predicts the existence of monopoles and strings―imaginable but untested quantum agents or beings, BDL is based on dipoles, particle-anti- particle pairs, action-reaction and input-output which are well-observed physical realities. Although it is a long tradition in logic and mathematics to treat +1 and −1 as isomorphic pairs, but no physicist would say electron is isomorphic to positron and no scientist would ask their children to learn math without negative numbers. The Nobel Prize level discoveries on parity non-conservation and CP-violation have proven the non-isomorphic bipolar coexistence of the negative and positive poles or the Yin and Yang of nature in a dynamic equilibrium of symmetry or broken symmetry. After all, BDL is a dynamic generalization from the static truth domain to the dynamic equilibrium domain. The latter can be deemed a domain of holistic truth with logically definable causality.
4.3.7. BDL Presents an Equilibrium-Based Axiomatization for Physics
Following the 2nd law of thermodynamics, BDL leads to a supersymmetrical bipolar equilibrium-based axiomatization of physics as shown in Table 4―a minimal but most general solution to Hilbert Problem 6―“Axioma- tizing all of physics” [104] . After a century, Hilbert’s Problem 6 is now widely deemed unsolvable. With the minimal but most general solution we have the prediction that, although Hilbert Problem 6 is not solvable with truth-based reasoning, it is solvable with equilibrium-based reasoning [9] [105] .
4.3.8. BDL Can Be Used for Revealing the Ubiquitous Effect of Quantum Entanglement
British mathematical physicist Roger Penrose identified two mysteries of quantum entanglement ( [93] , p. 591). The first is characterized as the phenomenon itself. The second, according to Penrose, is “How are we to come to terms with quantum entanglement and to make sense of it in terms of ideas that we can comprehend, so that we can manage to accept it as something that forms an important part of the workings of our actual universe?... The second mystery is somewhat complementary to the first. Since according to quantum mechanics, entanglement is such a ubiquitous phenomenon―and we recall that the stupendous majority of quantum states are actually entangled ones―why is it something that we barely notice in our direct experience of the world? Why do these ubiquitous effects of entanglement not confront us at every turn? I do not believe that this second mystery has received nearly the attention that it deserves, people’s puzzlement having been almost entirely concentrated on the first.”
BDL can be used for revealing the ubiquitous effects of quantum entanglement in social, mental, and biological worlds as well as logical and physical worlds [9] [105] . The possible revelations are due to the fact that BDL is based on bipolar sets whose elements can be entangled bipolar agents with the fundamental properties of (1) dipoles, particle-antiparticle and action-reaction pairs, negative-positive energies; (2) genomic repression-acti- vation of the ubiquitous genomic regulator protein Yin Yang 1 [63] and input-output energies of any biological system at the molecular, cell or organism levels; (3) competition-cooperation in socioeconomics; (3) self-negation and self-assertion abilities in mental health; (4) quantum bipolarity for quantum-digital compatibility in quantum computing ([9] , Ch 7).
It is evident from Figure 6 that, without bipolar quantum entanglement, there would be no atom-atom level entanglement. Therefore, it can be posited that bipolar quantum entanglement as a basic type of entanglement may lead to quantum-digital computing and communication with a number of advantages such as breakthroughs in teleportation, bitwise-encryption, quantum-digital compatibility, and enhanced security ([9] , Ch 7) [33] .
In the social world, an example bipolar cognitive map (BCM) of international competition-cooperation relation after the cold war is shown in Figure 11 together with its bipolar transitive closure (see Equation (14))―an entangled causal equilibrium relation [57] . Such an equilibrium relation can be used to classify the countries into different coalition, conflict and harmony clusters for multiagent decision analysis, prediction and coordination [57] [58] .
In the mental world, an application example of bipolar causal inference in psychiatric medicine is illustrated in Figure 12 [72] . Figure 12(a) shows the standard classification of bipolar disorders in the Diagnostic Statistics Manual (DSM-IV); Figure 12(b) shows a reshape with logical marking; Figure 12(c) shows the logical transformation of bipolar symptoms to YinYang bipolar geometry for bipolar causal inference.

Figure 11. A bipolar cognitive map and its Å-Ä transitive equilibrium relation.

Figure 12. Logical transformation of a DSM-IV standard to bipolar geometry.
4.3.9. BDL Leads to a Reincarnation of Philosophy
Due to its lack of a formal logical basis, the Dao of YinYang has never reached the status of science philosophy. With BDL, the Dao of YinYang leads to an equilibrium-based scientific reincarnation of philosophy [97] . It can be deemed a unification of science and philosophy as evidenced by the fact that BDL is a philosophical logic but also a formal mathematical logic with an equilibrium-based axiomatization of physics. On the other hand, it is a unification of reductionism and emergence. While reduction to absolute being and truth has been widely deemed impossible, reduction to bipolar dynamic equilibrium seems to be possible because the universe is believed a dynamic equilibrium of particles and antiparticles or negative and positive energies. From a different perspective, bipolarity has led to a completely background independent YinYang geometry that makes the emergence of being and truth possible through equilibrium-based causality or quantum entanglement. Namely, space and time can be effects caused by bipolar interaction and can emerge in the new geometry [77] [97] .
It should be remarked that YinYang is fundamentally different from Western metaphysics and dialectics. While Western metaphysics is truth-based and dialectics is contradiction-based, YinYang is equilibrium-based. Evidently, the equilibrium of negative and the positive poles or the input and output as a fundamental scientific concept has nothing contradictory. This is further supported by the fact that, while dialectics is not a formal logic and accused of obscurity and idealism or materialism, BDL has been shown a formal non-linear bipolar dynamic generalization of Boolean logic.
With energy-information unity, BDL can also be deemed a unification of realism and idealism. The word “realism” used to bear with two fundamentally different philosophical connotations: Platonic realism or Aristotelian realism. The disparity is originated from the historical student-teacher dispute between Aristotle and Plato. Platonic realism is usually used to refer to the idea of universals or abstract objects. As universals were considered by Plato to be ideal forms, this stance is also confusingly called Platonic idealism. In Aristotle’s view, however, universals exist only where they are instantiated; they exist only in things, never apart from things. Scientific local realism has taken Aristotle’s side for most of the times. Now the phenomena of quantum entanglement, global economy, and global warming are changing the tide. Many believe that local realism is unrealistic in the quantum world. The equilibrium-based approach to quantum entanglement seems to present a logical unification of both sides, where Aristotle’s local realism (as advocated in the EPR argument) is accounted for by truth-object(s) hosted in local equilibrium or non-equilibrium and Platonic global realism or idealism (as advocated by Bohr’s quantum non-locality) is accounted for with global equilibrium or non-equilibrium. Thus, BDL and BQLA make it both philosophically and scientifically possible to have local realism embedded into a deeper reality in which undivided wholeness prevails [40] . It is interesting to notice that, the deeper reality seems to satisfy Einstein’s concept of causality with (a) regularity; (b) locality; (c) symmetry considerations leading to conservation laws; (d) mutuality of causal interaction [34] .
4.3.10. BDL Leads to Mind-Body Unity
Mind-body duality or dichotomy has been a major barrier to the understanding of human intelligence. The origin of this barrier has been an unsolved mystery in science. With the equilibrium-based approach to logical and mathematical computation, the origin is located and the barrier is penetrated. Specifically, because truth and falsity form a dichotomy, truth-based reasoning cannot reach mind-body unity. Therefore, the barrier has been virtually a conceptual one right in our own mind for all the centuries.
Since mind and body can be both hosted in the equilibrium-based background independent YinYang bipolar geometry (Figure 10), the equilibrium-based approach brings the mind-body dichotomy into a holistic logical unity based on energy-information unity. Since our mind can be characterized as an entanglement of multidimensional dynamic equilibrium states with neuro-biological, neuro-chemical, neuro-electromagnetic, neuro-dynamic and other quantum dynamic aspects, mind and body together can be modeled as a unitary quantum agent (Figure 6, Figure 7) to which the causation laws (Laws 1 - 9) provide an axiomatic basis for quantum intelligence. A simple example is image-vocabulary-sound-taste mental entanglement of a fruit such as an apple. When we think about an apple, we have a mental image that may be entangled to the word “apple”, its pronunciation and its taste. While a truth-based approach provides no logically definable entanglement, equilibrium- based bipolar quantum entanglement lends itself as a formal analytical system for causal propagation with mind- body unity. This hypothetical example points to an equilibrium-based approach to associative memory modeling for future research.
5. Challenges
QAQI is faced with numerous challenges. Three of them are outlined in this section.
5.1. Equilibrium-Based Logical Completeness
A major theoretical challenge is to prove equilibrium-based completeness of BDL. Gödel’s incompleteness theorems [106] stand out as a landmark in truth-based logical reasoning that has been deemed by many as impassable. His first incompleteness theorem shows that systems having at least the properties of Peano arithmetic cannot be both complete and consistent. Gödel’s 2nd incompleteness theorem shows that no system with such properties can be proven consistent within itself, unless it is an inconsistent system. But BDL and BQLA as a non-linear bipolar dynamic generalization of Boolean logic from truth domain to equilibrium (or holistic truth) domain must supersets Peano arithmetic and has to overturn Gödel’s two theorems by proving its own consistency within itself. Otherwise, there must be a further generalization to supersets the equilibrium-based one.
It is reported that, the ancient paradox of the liar was the original inspiration for Gödel’s incompleteness theorems ( [107] , p. 221). The paradox, which was known even to Aristotle, consists of a single sentence L “This sentence is not true”. If L is true, then L is not true. Thus, L is both true and false. But that is against the fundamental law of non-contradiction. So we have the liar paradox.
Subsequently, a key for an overturn of Gödel’s incompleteness theorems is the elimination of the liar paradox. Evidently, the four values of BDL are equilibrium (−1, +1), non-equilibrium (−1, 0), non-equilibrium (0, +1), and eternal equilibrium (0, 0), where the liar’s paradox is left no room. However, a formal overturn of Gödel’s incompleteness theorems still remains a great theoretical challenge in logical reasoning which is left open for further research effort. It is predicted that, although Gödel’s incompleteness theorems cannot be overturned by any truth-based logical system, it can be overturned by an equilibrium-based one [105] .
5.2. Transformation of Equilibrium-Based Causality to Truth-Based Representation
Under certain condition, bipolar quantum causality is deterministic in equilibrium-based terms. But equilibrium is not as self-evident as truth-based representation. A major theoretical as well as practical challenge is the transformation of equilibrium-based causality to truth-based representation. Such transformation is expected to result in major applications:
・ Quantum computing so far largely remains a truth-based approach that inherits some binary features from classical digital computing. This heritage has never been challenged. Bipolar quantum logic gates present an equilibrium-based approach to quantum computing [33] . Equilibrium-based to truth-based causality transformation may lead to bipolar coding for quantum-digital compatibility and bitwise encryption in quantum computing and communication.
・ The transformation may find major applications in computational biology and breakthroughs in quantum biology [108] .
・ It may play a pivotal role in the understanding as well as the modeling of memory formation and brain system organization of biological and artificial agents for quantum computational intelligence as well as quantum cognition [109] .
・ It may play a pivotal role in quantum cosmology and astrophysics.
・ It may find major applications in economics and social science.
・ It may lead to breakthroughs in medical science especially in holistic medicine such as Traditional Chinese Medicine (TCM).
5.3. Quantum Data Mining and Knowledge Discovery
A major advantage of bipolar causal reasoning lies in its bipolar inductive reasoning as well as deductive reasoning (see Theorems 1 - 2). While bipolar deductive reasoning leads to effects from causes, bipolar inductive reasoning can be used to determine hidden causes from observed effects. Thus, applying bipolar causal reasoning for data mining and knowledge discovery presents another major potential and another major challenge. As an alternative to truth-based association rule mining and knowledge discovery, an advantage of bipolar association is to take into account of both negative and positive sides in a holistic way for a category of major decision tasks. A major challenge is how to identify bipolar agents and then mine bipolar association rules for physical, biological, mental, medical and socioeconomical predictions.
Case 1. Exploratory Scientific Knowledge Discovery
Let y = (y−, y+) = (negative, positive) be a bipolar predicate and a, b, c, d be any four bipolar subatomic particles that can change polarity [78] . "a, b, c, d with time t and space p, we have:
[(y(a(tx, p1)) Þ y(c(ty, p3)))&(y(b(tx, p2)) Þ y(d(ty, p4)))]
Þ[(y(a(tx, p1))*y (b(tx, p2))) Þ (y(c(ty, p3))*y(d(ty, p4)))]
Þ [y(a(tx, p1)¨b(tx, p2)) Þ y(c(ty, p3)¨d(ty, p4))].
Evidently, any proof of association in the above logical equation could lead to a major scientific discovery. But the difficulty is how to identify bipolar associations in the precedents with time t and space p and a supporting probability x and y as
(1) y(a(tx, p1))Þy(c(ty, p3)), support = x% and
(2) y(b(tx, p2))Þy(d(ty, p4)), support = y%.
Case 2. Bioinformatics Data Mining and Knowledge Discovery
Quantum computing is warming up. Quantum computers are expected to add tremendous computational speed and power to scientific explorations into the microscopic and macroscopic agent worlds. The quantum nature of biological agents, however, is still a mystery. Ball’s Nature News reports [53] predict that “The key to practical quantum computing and high-efficiency solar cells may lie in the messy green world outside the physics lab”. Ball cited research results from two teams [108] to back his claim up.
Quantum biology refers to applications of quantum mechanics to biological agents and problems. These applications entail the “non-trivial” quantum features such as superposition, non-locality, entangled tunneling, as opposed to the so-called “trivial” but ubiquitous quantum mechanical nature of chemical bonding, ionization, and other phenomena that are the basis of the fundamental biophysics and biochemistry of organisms. Few have, however, attempted to unify the two features into a fundamental quantum theory for bioinformatics and computational biology. A barrier to the unification is the unknown quantum causality which has been long deemed unattainable.
The impassable barrier has been penetrated by BUMP. Let y = (y−, y+) = (repression, activation) be a bipolar predicate for the abilities of regulator genomic agents such as YY1 [63] ; let f = (f−, f+) = (repressability, activatability) be a predicate for the bipolar capacities of regulated agents; let (c−, c+) and (j−, j+) be any bipolar predicates; let a, b, c, d be any agents. YinYang bipolar quantum entanglement or BUMP can be deemed a fundamental law for equilibrium-based regulation of gene expression, mutation, and molecular interaction in bioinformatics. Formally, "a, b, c, d with time t and space p, we have (note: * and ¨ can be bound to granular bipolar logical or physical operators):
(1) [y(a(tx, p1)) Þ f(c(ty, p3))]&[y(b(tx, p2)) Þ f(d(ty, p4))] Þ [y(a(tx, p1))*y(b(tx, p2)) Þ f(c(ty, p3))*f(d(ty, p4))] Þ [y(a(tx, p1)¨b(tx, p2)) Þ f(c(ty, p3)¨d(ty, p4))];
(2) [y(a(tx, p1)) Þ y(c(ty, p3))]&[f(b(tx, p2)) Þ f(d(ty, p4))] Þ [y(a(tx, p1))*f(b(tx, p2)) Þ y(c(ty, p3))*f(d(ty, p4))].
The key here is BDL, which has been shown a non-linear bipolar dynamic generalization of Boolean logic from the truth-based world to the bipolar dynamic equilibrium-based world. While in truth-based terms a bipolar agent (such as YY1) cannot be a truth object, in equilibrium-based terms any bipolar agent can be a holistic truth object. The challenge is, however, how to mine equilibrium-based association patterns.
Case 3. Psychopharmacology Data Mining and Knowledge Discovery
Let y = (y−, y+) = (self-negation, self-assertion) be a bipolar predicate for the mental equilibrium measures of a patient set P at the neurophysiologic level; let (c−, c+) be that of the set P at the mood or behavior level; let f = (f−, f+) = (negative, positive) be a bipolar predicate for the biochemical capacities of a medicine set M for bipolar disorders; let (j−, j+) = (un-excite, un-depress) be that for the effects of M at the mental level. "a, b, a Î P and b Î M, we have
[(y(a(tx)) Þ c(a(ty)))]&[(f(b(tx)) Þ j(b(ty)))] Þ y(a(tx))*f(b(tx))) Þ (c(a(ty))*j(b(ty)))].
The above rule could be discovered as a fundamental law of equilibrium-based brain and behavior, which may be applied in nanobiomedicine for psychiatric mood regulation on an individual and/or a cohort of mental disorder patients. However, its discovery and application post a great challenge which may entail bipolar equilibrium-based probability and statistics―a new area of research
For instance, given the text data in Table 7, how to answer the question: What specific granular bipolar fuzzy operator (*) should be used to characterize the neurobiological reactions of a specific or a cohort of patients to their medical treatments or external stimuli? [73]
Regardless of the difficulty in equilibrium-based data mining, interestingly, bipolar data and knowledge visualization can be supported with bipolar geometry used as a supporting vector machine [73] (Figure 13).
6. Conclusions
A survey on agents, causality and intelligence has been presented and a computing paradigm of QAQI has been proposed. In the survey, Aristotle’s causality principle and its historical extensions by David Hume, Bertrand Russell, Lotfi Zadeh, Donald Rubin, Judea Pearl, Niels Bohr, Albert Einstein, David Bohm, and the causal set initiative have been reviewed; bipolar dynamic logic (BDL) and bipolar quantum linear algebra (BQLA) have been introduced for causal inference.
Despite the widely held view that causality is undefinable with regularity, it has been shown that equilibrium- based bipolar causality is logically definable with BDL and BQLA for causal inference in physical, social, biological, mental as well as philosophical terms. This finding has led to the paradigm of QAQI. In this paradigm,
Table 7. Text for bipolar data mining.

Figure 13. Bipolar geometry as a generic supporting vector machine for bipolar disorder data and knowledge visualization.
agents in different domains are modeled as quantum ensembles; intelligence is revealed as quantum intelligence; the ensemble formation and change of agents are deemed direct or indirect results of quantum causality starting from quantum interaction and quantum entanglement.
While quantum computing has been focused on developing quantum computers with superposition and quantum entanglement for solving unsolved computational problems, it has been shown that BDL, BQLA and bipolar quantum logic gates provide a formal analytical basis for QAQI. The ubiquitous nature of QAQI has been examined and distinguished from other paradigms. Some major challenges have been identified in equilibrium- based bipolar causal inference, data mining, and knowledge discovery.
It has been shown that logically definable causality led to a number of causation laws and unifications, including but not limited to particle-wave unification, energy-information unification and mind-body unification. These laws have made generic and composite quantum causality logically and mathematically reachable. In particular, the laws have unified quantum agent interaction, quantum entanglement, quantum information, and quantum intelligence.
It should be remarked that
・ As a non-linear bipolar dynamic generalization of Boolean logic from the truth-based domain {0, 1} to the equilibrium-based domain {−1, 0}×{0, +1}, BDL makes equilibrium-based causality logically definable but has truth-based logic embedded and does not exclude truth-based logical reasoning and causal inference. On the other hand, the generalization cannot be denied unless being, truth and the universe could escape from bipolar dynamic equilibrium. This fact shows that BDL is a unitary generalization from static truth to dynamic truth. It reflects the reality that any being or agent is fundamentally a bipolar dynamic equilibrium of input and output energies―the origin of information.
・ As a causal logic, BDL does not exclude probabilistic and statistical causal reasoning. Instead, bipolar causal inference has opened an equilibrium-based approach to randomness, probability and statistics that post a great challenge to equilibrium-based bipolar data mining and explorative knowledge discovery.
・ “Causality is logically definable” has been presented as an equilibrium-based logical theory with illustrations of applicability. While no being or truth can escape from equilibrium or non-equilibrium, it does not suggest that all practical causal relations can be formulated as logical equations without exception. Practically, the search for truth and equilibrium is a forever lasting process. It is certain though that the equilibrium-based and truth-based approaches can complement each other in problem solving especially when and where dynamic equilibrium is central.
・ Quantum intelligence (QI) is more general than quantum artificial intelligence (QAI). While QAI may take advantage of the high speed of quantum computing for machine intelligence or data mining, QI is focused on quantum causality for causal inference with the basic assumption that all agents are formed with a collection of subatomic (quantum) particles and the existence of all agents and their changes in the real world are due to quantum causality where equilibrium-based bipolar causality is posited most fundamental. Moreover, QI attempts to reveal the nature of quantum entanglement and its ubiquitous cause-effects. That has been deemed impossible in quantum mechanics and quantum computing. It is made possible with BDL and BQLA, which as non-linear generalizations of Boolean logic and classical linear algebra, respectively, have built a logical bridge from the truth-based agent world to the equilibrium-based quantum agent world.
・ While quantum mechanics and quantum computing have been positioned in spacetime geometry, the QAQI paradigm has been presented in the background independent YinYang bipolar geometry that transcends spacetime geometry. Space and time dimensions can, however, be added to YinYang bipolar geometry as emerging factors due to bipolar interaction or entanglement when and where necessary without losing generality.
・ The equilibrium-based approach to causality is deterministic under certain conditions. However, equilibrium-based representation may needs a transformation to truth-based knowledge representation for data mining and visualization. This is left for future research effort.
It is interesting to answer a few questions:
(1) “How could your logic be used to represent the fact that tree leaves are green?”
The answer to this question is simple. On one hand, since truth-based logic is embedded in BDL, it is part of the generalization. Therefore, truth-based knowledge representation and logical reasoning can still be used freely as long as it does not violate the equilibrium or non-equilibrium conditions of the laws of thermodynamics. On the other hand, since dynamic equilibrium is the essence of growing and aging of an agent, the color change of tree leaves from green to yellow is caused by a dynamic equilibrium of photosynthesis with logically definable quantum causality―a focal point of this work.
(2) “Isn’t bipolar dynamic equilibrium contradictory?”
The answer is NO. When a sentence is both true and false, we have a contradiction. When the negative pole and the positive pole (or the input and output) of one agent are balanced, we have a dynamic equilibrium that has nothing contradictory as we say “the universe is a dynamic equilibrium” and we don’t say “the universe is a contradiction”.
(3) “BDL is too simple but why is it so confusing?”
BDL is once said too simple by one reviewer but too confusing by another. Evidently, BUMP is simple but more complex than MP and BDL at the elementary level is also simple but significantly more complex than any truth-based logic. As Niels Bohr famously stated, “Those who are not shocked when they first come across quantum theory cannot possibly have understood it”. It is natural to feel confused sometimes. Nevertheless, BDL has built an equilibrium-based logical bridge from the truth-based world to the quantum world that makes quantum causality and entanglement definable in simple logically comprehendible terms and forms. Hopefully, one of its significance lies in its simplicity in resolving the confusion.
(4) “How could your logic lead to so many different unifications so easily? Wouldn’t that be pseudoscience?”
The answer to this question is also simple. First, any logically definable causality must show its computational power for a number of unifications. Otherwise, the theory would be incorrect or scientifically and philosophically trivial. Secondly, if our universe is regulated by negative and positive energies and consists of particles and antiparticles which can survive both a big bang and a black hole, bipolarity, instead of truth, has to be the most fundamental property of the universe and bipolar dynamic equilibrium has to be the most generic form of any equilibrium or non-equilibrium. Since equilibrium or non-equilibrium is central in the laws of thermodynamics, BDL can be deemed a logical formulation of these laws from which nothing can escape as we say “everything in the universe including the universe itself comes to exist as a dynamic equilibrium or non-equilibrium” and we don’t say “everything in the universe including the universe itself comes to exist as static truth and/or falsity”. Since the laws of thermodynamics are paramount in modern science that provides the ultimate source of causality for existence, energy, life, and information, a sound logical formulation of these laws has to be scientific but not pseudoscientific in nature, unless it is logically falsified. Furthermore, it is a well-known fact that, while ether, monad, monopoles and strings are imaginable quantum agents but so far untestable, dipoles, particle-an- tiparticle pairs and action-reaction as the most fundamental elements of the universe are observed everywhere. If, without logically definable causality, Leibniz binary interpretation and Bohr’s particle-wave interpretation of YinYang are both scientific, the bipolar interpretation with logically definable causality should be more scientific unless double standards are used.
(5) “Philosophy is not science, why should it be part of your work?”
This question is best answered with a quote from Einstein. A letter from Einstein to R. A. Thornton dated Dec. 7, 1944 wrote (cf. [10] , pp. 310-311): I fully agree with you about the significance and educational value of methodology as well as history and philosophy of science. So many people today―and even professional scientists ―seem to me like someone who has seen thousands of trees but has never seen a forest. A knowledge of the historical and philosophical background gives that kind of independence from prejudices of his generation from which most scientists are suffering. This independence created by philosophical insights is―in my opinion―the mark of distinction between a mere artisan or specialist and a real seeker after truth.
Acknowledgements
The authors acknowledge all reviewers of earlier versions of this work for their critical and constructive comments.
Cite this paper
Wen-RanZhang,Karl E.Peace, (2014) Causality Is Logically Definable—Toward an Equilibrium-Based Computing Paradigm of Quantum Agent and Quantum Intelligence (QAQI) (Survey and Research). Journal of Quantum Information Science,04,227-268. doi: 10.4236/jqis.2014.44021
References
- 1. Hume, D. (1738) A Treatise of Human Nature. Norton, D.F. and Norton, M.J., Eds., Oxford University Press, Oxford/ New York.
- 2. Hume, D. (1748) An Enquiry Concerning Human Understanding. Renascence Editions.
https://scholarsbank.uoregon.edu/xmlui/bitstream/handle/1794/747/hume.pdf - 3. Blackburn, S. (1990) Hume and Thick Connexions. Philosophy and Phenomenological Research, 50, 237-250.
http://dx.doi.org/10.2307/2108041 - 4. Russell, B. (1913) On the Notion of Cause. Proceedings of the Aristotelian Society, 13, 1-26.
- 5. Bohr, N. (1948) On The Notions of Causality and Complementarity. Dialectica, 2, 312-319.
http://dx.doi.org/10.1111/j.1746-8361.1948.tb00703.x - 6. Zadeh, L.A. (2001) Causality Is Undefinable—Toward a Theory of Hierarchical Definability. The 10th IEEE International Conference on Fuzzy Systems, 2-5 December 2001, 67-68.
- 7. Zadeh, L.A. (2008) Fuzzy Logic. Scholarpedia, 3, 1766.
http://dx.doi.org/10.4249/scholarpedia.1766 - 8. Zhang, W.-R. (1998) YinYang Bipolar Fuzzy Sets. Proceedings of IEEE World Congress on Computational Intelligence, Anchorage, May 1998, 835-840.
- 9. Zhang, W.-R. (2011) YinYang Bipolar Relativity: A Unifying Theory of Nature, Agents and Causality with Applications in Quantum Computing, Cognitive Informatics and Life Sciences. IGI Global, Hershey and New York.
http://dx.doi.org/10.4018/978-1-60960-525-4 - 10. Smolin, L. (2006) The Trouble with Physics: The Rise of String Theory, the Fall of a Science, and What Comes Next? Houghton Mifflin Harcourt, New York.
- 11. Woit, P. (2006) Not Even Wrong: The Failure of String Theory and the Search for Unity in Physical Law. Basic Book, New York, 2006.
- 12. Bub, J. (2006) Quantum Entanglement and Information. Stanford Encyclopedia of Philosophy.
http://plato.stanford.edu/entries/qt-entangle/ - 13. Bell, J.S. (1964) On the Einstein Podolsky Rosen Paradox. Physics, 1, 195-200.
- 14. Hawking, S. and Penrose, R. (1970) The Singularities of Gravitational Collapse and Cosmology. Proceedings of the Royal Society A, 314, 529-548.
http://dx.doi.org/10.1098/rspa.1970.0021 - 15. Hawking, S. (1974) Black Hole Evaporation. Nature, 248, 30-31.
http://dx.doi.org/10.1038/248030a0 - 16. Hawking, S. (1975) Particle Creation by Black Holes. Communications in Mathematical Physics, 43, 199-220.
http://dx.doi.org/10.1007/BF02345020 - 17. Cazalilla, M.A. and Rigol, M. (2010) Focus on Dynamics and Thermalization in Isolated Quantum Many-Body Systems. New Journal of Physics, 12, Article ID: 055006.
http://dx.doi.org/10.1088/1367-2630/12/5/055006 - 18. Falcon, A. (2008) Aristotle on Causality. Stanford Encyclopedia of Philosophy.
http://plato.stanford.edu/entries/aristotle-causality/ - 19. Morris, W.E. (2009) David Hume. Stanford Encyclopedia of Philosophy.
http://plato.stanford.edu/ entries/hume/ - 20. Russell, B. (1948) Human Knowledge. Simon & Schuster, New York.
- 21. Russell, B. (1945) A History of Western Philosophy. Simon & Schuster, New York.
- 22. Lewis, D. (1973) Causation. Journal of Philosophy, 70, 556-567.
http://dx.doi.org/10.2307/2025310 - 23. Mackie, J.L. (1974) The Cement of the Universe. Oxford University Press, Oxford.
- 24. Von Wright, G.H. (1975) On the Logic and Epistemology of the Causal Relation. Oxford University Press, Oxford, 95-113.
- 25. Rorty, R. (1989) Contingency, Irony, and Solidarity. Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/CBO9780511804397 - 26. Russell, B. (1919) Introduction to Mathematical Philosophy. Routledge Inc., London.
- 27. Rubin, D. (1974) Estimating Causal Effects of Treatments in Randomized and Nonrandomized Studies. Journal of Educational Psychology, 66, 688-701.
http://dx.doi.org/10.1037/h0037350 - 28. Rubin, D. (1978) Bayesian Inference for Causal Effects: The Role of Randomization. The Annals of Statistics, 6, 34-58.
http://dx.doi.org/10.1214/aos/1176344064 - 29. Rosenbaum, P. and Rubin, D. (1983) The Central Role of the Propensity Score in Observational Studies for Causal Effects. Biometrika, 70, 41-55.
http://dx.doi.org/10.1093/biomet/70.1.41 - 30. Pearl, J. (1988) Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference. Morgan Kaufmann Publishers, San Mateo, 1988.
- 31. Pearl, J. (2000) Causality: Models, Reasoning, and Inference. Cambridge University Press, Cambridge.
- 32. Pearl, J. (2009) Causal Analysis in Theory and Practice—More on Pearl’s and Robin’s Frameworks for Causal Inference— Discussion.
http://www.mii.ucla.edu/causality/?p=57 - 33. Zhang, W.-R. (2013) Bipolar Quantum Logic Gates and Quantum Cellular Combinatorics—A Logical Extension to Quantum Entanglement. Journal of Quantum Information Science, 3, 93-105.
http://dx.doi.org/10.4236/jqis.2013.32014 - 34. Ben-Menahem, Y. (1993) Struggling with Causality: Einstein’s Case. Science in Context, 6, 291-310.
http://dx.doi.org/10.1017/S0269889700001393 - 35. Einstein, A., Podolsky, B. and Rosen, N. (1935) Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Physical Review, 47, 777-780.
http://dx.doi.org/10.1103/PhysRev.47.777 - 36. Einstein, A. (1916) The Foundation of the General Theory of Relativity. Annalen der Physik, 49, 769-822.
http://dx.doi.org/10.1002/andp.19163540702 - 37. Einstein, A. (1934) On the Method of Theoretical Physics. The Herbert Spencer Lecture, Mein Weltbild, Querido Verlag, Amsterdam.
- 38. Einstein, A. (1940) Considerations Concerning the Fundaments of Theoretical Physics. Science, 91, 487-491.
http://dx.doi.org/10.1126/science.91.2369.487 - 39. Einstein, A. (1953) Famous Letter to J. E. Switzer. [cf. de Solla Price, D. (1963) Science since Babylon. Yale University Press, New Haven, 15, Note 10.]
- 40. Bohm, D. (1980) Wholeness and the Implicate Order. Routledge, London.
- 41. Bohm, D. (1957) Causality and Chance in Modern Physics. Routledge & Kegan Paul and D. Van Nostrand.
- 42. Bell, J.S. (1964) On the Einstein-Podolsky-Rosen Paradox. Physics, 1, 195-200.
- 43. Kumar, M. (2008) Quantum: Einstein, Bohr, and the Great Debate about the Nature of Reality. Norton & Company, New York, London.
- 44. Bombelli, L., Lee, J., Meyer, D. and Sorkin, R.D. (1987) Spacetime as a Causal Set. Physical Review Letters, 59, 521-524.
http://dx.doi.org/10.1126/science.91.2369.487 - 45. Malament, D. (1977) The Class of Continuous Timelike Curves Determines the Topology of Spacetime. Journal of Mathematical Physics, 18, 1399-1404.
http://dx.doi.org/10.1063/1.523436 - 46. Dowker, F., Henson, J. and Sorkin, R. (2004) Quantum Gravity Phenomenology, Lorentz Invariance and Discreteness. Modern Physics Letters A, 19, 1829-1840.
http://dx.doi.org/10.1142/S0217732304015026 - 47. Dowker, F. (2006) Causal Sets as Discrete Spacetime. Contemporary Physics, 47, 1-9.
http://dx.doi.org/10.1080/17445760500356833 - 48. Bombelli, L., Henson, J. and Sorkin, R.D. (2009) Discreteness without Symmetry Breaking: A Theorem. Modern Physics Letters A, 24, 2579-2587.
http://dx.doi.org/10.1142/S0217732309031958 - 49. Bombelli, L., Corichi, A. and Winkler, O. (2009) Semiclassical Quantum Gravity: Obtaining Manifolds from Graphs. Classical and Quantum Gravity, 26, Article ID: 245012.
http://dx.doi.org/10.1088/0264-9381/26/24/245012 - 50. Gottfredson, L.S. (1997) Mainstream Science on Intelligence: An Editorial with 52 Signatories, History, and Bibliography. Intelligence, 24, 13-23.
http://dx.doi.org/10.1016/S0160-2896(97)90011-8 - 51. Neisser, U., Boodoo, G., Bouchard, T.J., Boykin, A.W., Brody, N., Ceci, S.J., Halpern, D.F., Loehlin, J.C., Perloff, R., Sternberg, R.J. and Urbina, S. (1996) Intelligence: Knowns and Unknowns. American Psychologist, 51, 77-101.
http://dx.doi.org/10.1037/0003-066X.51.2.77 - 52. Neisser, U., Boodoo, G., Bouchard Jr, T.J., Boykin, A.W., Brody, N., Ceci, S.J., Halpern, D.F., Loehlin, J.C., Perloff, R., Sternberg, R.J., et al. (1998) Intelligence: Knowns and Unknowns. Annual Progress in Child Psychiatry and Child Development, Board of Scientific Affairs of the American Psychological Association.
- 53. Ball, P. (2011) Physics of Life: The Dawn of Quantum Biology. Nature, 474, 272-274.
http://dx.doi.org/10.1038/474272a - 54. Moran, E. and Yu, J. (2001) The Complete Idiot’s Guide to the I Ching. Alpha Books, New York.
- 55. Leibniz, G. (1703) Explication de l’Arithmétique Binaire (Explanation of Binary Arithmetic). Mathematical Writings VII, Gerhardt, 223.
- 56. Hawking, S. and Mlodinow, L. (2010) The Grand Design. Random House Digital, Inc., New York.
- 57. Zhang, W.-R. (2003) Equilibrium Relations and Bipolar Cognitive Mapping for Online Analytical Processing with Applications in International Relations and Strategic Decision Support. IEEE Transactions on Systems, Man, and Cybernetics, Part B, 33, 295-307.
http://dx.doi.org/10.1109/TSMCB.2003.810444 - 58. Zhang, W.-R. (2003) Equilibrium Energy and Stability Measures for Bipolar Decision and Global Regulation. International Journal of Fuzzy Systems, 5, 114-122.
- 59. Zhang, W.-R. and Zhang, L. (2004) YinYang Bipolar Logic and Bipolar Fuzzy Logic. Information Sciences, 165, 265-287.
http://dx.doi.org/10.1016/j.ins.2003.05.010 - 60. Zhang, W.-R. (2005) YinYang Bipolar Lattices and L-Sets for Bipolar Knowledge Fusion, Visualization, and Decision. International Journal of Information Technology & Decision Making, 4, 621-645.
http://dx.doi.org/10.1142/S0219622005001763 - 61. Zhang, W.-R. (2006) YinYang Bipolar Fuzzy Sets and Fuzzy Equilibrium Relations for Bipolar Clustering, Optimization, and Global Regulation. International Journal of Information Technology & Decision Making, 5, 19-46.
http://dx.doi.org/10.1142/S0219622006001885 - 62. Gore, J. and Van Oudenaarden, A. (2009) Synthetic Biology: The Yin and Yang of Nature. Nature, 457, 271-272.
http://dx.doi.org/10.1038/457271a - 63. Shi, Y., Seto, E., Chang, L.-S. and Shenk, T. (1991) Transcriptional Repression by YY1, a Human GLI-Kruppel-Related Protein, and Relief of Repression by Adenovirus E1A Protein. Cell, 67, 377-388.
http://dx.doi.org/10.1016/0092-8674(91)90189-6 - 64. Ai, W., Narahari, J. and Roman, A. (2000) Yin Yang 1 Negatively Regulates the Differentiation-Specific E1 Promoter of Human Papillomavirus Type 6. Journal of Virology, 74, 5198-5205.
http://dx.doi.org/10.1128/JVI.74.11.5198-5205.2000 - 65. Palko, L., Bass, H.W., Beyrouthy, M.J. and Hurt, M.M. (2004) The Yin Yang-1 (YY1) Protein Undergoes a DNA-Replication-Associated Switch in Localization from the Cytoplasm to the Nucleus at the Onset of S Phase. Journal of Cell Science, 117, 465-476.
http://dx.doi.org/10.1242/jcs.00870 - 66. Zhou, Q. and Yik, J.H.N. (2006) The Yin and Yang of P-TEFb Regulation: Implications for Human Immunodeficiency Virus Gene Expression and Global Control of Cell Growth and Differentiation. Microbiology and Molecular Biology Reviews, 70, 646-659.
http://dx.doi.org/10.1128/MMBR.00011-06 - 67. Wilkinson, F.H., Park, K. and Atchison, M.L. (2006) Polycomb Recruitment to DNA in Vivo by the YY1 REPO Domain. Proceedings of the National Academy of Sciences USA, 103, 19296-19301.
http://dx.doi.org/10.1073/pnas.0603564103 - 68. Kim, J.D., Faulk, C. and Kim, J. (2007) Retroposition and Evolution of the DNA-Binding Motifs of YY1, YY2 and REX1. Nucleic Acids Research, 35, 3442-3452.
http://dx.doi.org/10.1093/nar/gkm235 - 69. Santiago, F.S., Ishii, H., Shafi, S., Khurana, R., Kanellakis, P., Bhindi, R., Ramirez, M.J., Bobik, A., Martin, J.F., Chesterman, C.N., Zachary, I.C. and Khachigian, L.M. (2007) Yin Yang-1 Inhibits Vascular Smooth Muscle Cell Growth and Intimal, Thickening by Repressing p21WAF1/Cip1 Transcription and p21WAF1/Cip1-Cdk4-Cyclin D1 Assembly. Circulation Research, 101, 146-155.
http://dx.doi.org/10.1161/CIRCRESAHA.106.145235 - 70. Liu, H., Schmidt-Supprian, M., Shi, Y., Hobeika, E., Barteneva, N., Jumaa, H., Pelanda, R., Reth, M., Skok, J., Rajewsky, K. and Shi, Y. (2007) Yin Yang 1 Is a Critical Regulator of B-Cell Development. Genes & Development, 21, 1179-1189.
http://dx.doi.org/10.1101/gad.1529307 - 71. Vasudevan, S., Tong, Y. and Steitz, J.A. (2007) Switching from Repression to Activation: Micro-RNAs Can Up-Regulate Translation. Science, 318, 1931-1934.
http://dx.doi.org/10.1126/science.1149460 - 72. Zhang, W.-R., Pandurangi, A. and Peace, K. (2007) YinYang Dynamic Neurobiological Modeling and Diagnostic Analysis of Major Depressive and Bipolar Disorders. IEEE Transactions on Biomedical Engineering, 54, 1729-1739.
http://dx.doi.org/10.1109/TBME.2007.894832 - 73. Zhang, W.-R., Pandurangi, K.A., Peace, K.E., Zhang, Y. and Zhao, Z. (2011) Mental Squares—A Generic Bipolar Support Vector Machine for Psychiatric Disorder Classification, Diagnostic Analysis and Neurobiological Data Mining. International Journal on Data Mining and Bioinformatics, 5, 532-557.
- 74. Valk, P.E., Bailey, D.L., Townsend, D.W. and Maisey, M.N. (2005) Positron Emission Tomography: Basic Sciences. Springer-Verlag, Secaucus.
- 75. Carey, B. (2007) Man Regains Speech after Brain Stimulation. The New York Times—Health.
http://www.nytimes.com/2007/08/01/health/01cnd-brain.html. - 76. Zhang, W.-R, Zhang, H.J., Shi, Y. and Chen, S.S. (2009) Bipolar Linear Algebra and YinYang-N-Element Cellular Networks for Equilibrium-Based Biosystem Simulation and Regulation. Journal of Biological Systems, 17, 547-576.
http://dx.doi.org/10.1142/S0218339009002958 - 77. Zhang, W.-R. (2012) YinYang Bipolar Atom—An Eastern Road toward Quantum Gravity. Journal of Modern Physics, 3, 1261-1271.
http://dx.doi.org/10.4236/jmp.2012.329163 - 78. Fermi National Accelerator Laboratory (2006) Press Release 06-19.
http://www.fnal.gov/pub/presspass/press_releases/CDF_meson.html - 79. Huhns, M. N., Ed. (1987) Distributed Artificial Intelligence. Pitman, London.
- 80. Huhns, M.N. and Singh, M.P. (1997) Readings in Agents. Morgan Kaufmann, Burlington.
- 81. Huhns, M.N. (2000) An Agent-Based Global Economy. IEEE Internet Computing, 4, 83-84.
- 82. Dang, J., Huang, J. and Huhns, M.N. (2007) Workflow Coordination for Service-Oriented Multiagent Systems. Proceeding of 6th International Conference on Autonomous Agents and Multiagent Systems (AAMAS-07), Honolulu, Hawaii, May 2007, 1049-1051.
- 83. Zhang, W.-R. (1998) Nesting, Safety, Layering, and Autonomy: A Reorganizable Multiagent Cerebellar Architecture for Intelligent Control with Application in Legged Locomotion and Gymnastics. IEEE Transactions on Systems, Man, and Cybernetics, Part B, 28, 357-375.
- 84. Zhang, W.-R. and Zhang, L. (2004) A Multiagent Data Warehousing (MADWH) and Multiagent Data Mining (MADM) Approach to Brain Modeling and Neuro-Fuzzy Control. Information Sciences, 167, 109-127.
http://dx.doi.org/10.1016/j.ins.2003.05.011 - 85. Zhang, W.-R., Chen, S. and Bezdek, J.C. (1989) POOL2: A Generic System for Cognitive Map Development and Decision Analysis. IEEE Transactions on Systems, Man, and Cybernetics, 19, 31-39.
http://dx.doi.org/10.1109/21.24529 - 86. Zhang, W.-R., Chen, S., Wang, W. and King, R. (1992) A Cognitive Map Based Approach to the Coordination of Distributed Cooperative Agents. IEEE Transactions on SMC, 22, 103-114.
- 87. Zhang, W.-R., Wang, W. and King, R. (1994) An Agent-Oriented Open System Shell for Distributed Decision Process Modeling. Journal of Organizational Computing, 4, 127-154.
http://dx.doi.org/10.1080/10919399409540220 - 88. Zhang, W.-R. (1996) NPN Fuzzy Sets and NPN Qualitative Algebra: A Computational Framework for Bipolar Cognitive Modeling and Multiagent Decision Analysis. IEEE Transactions on Systems, Man, and Cybernetics, 16, 561-574.
http://dx.doi.org/10.1109/3477.517031 - 89. Lloyd, S. (2006) Programming the Universe. Alfred A. Knopf, Inc., New York.
- 90. Salart, D., Baas, A., Branciard, C., Gisin, N. and Zbinden, H. (2008)Testing the Speed of “Spooky Action at a Distance”. Nature, 454, 861-864.
http://dx.doi.org/10.1038/nature07121 - 91. Bancal, J.-D., S. Pironio, Acin, A., Liang, Y.-C., Scarani, V. and Gisin, N. (2012) Quantum Non-Locality Based on Finite-Speed Causal Influences Leads to Superluminal Signalling. Nature Physics, 8, 867-870.
http://dx.doi.org/10.1038/nphys2460 - 92. Yin, J., Cao, Y., Yong, H.-L., Ren, J.-G., Liang, H., Liao, S.-K., Zhou, F., Liu, C., Wu, Y.-P., Pan, G.-S., Li, L., Liu, N.-L., Zhang, Q., Peng, C.-Z. and Pan, J.-W. (2013) Bounding the Speed of “Spooky Action at a Distance”.
arXiv:1303.0614v2 [quant-ph] - 93. Penrose, R. (2005) The Road to Reality: A Complete Guide to the Laws of the Universe. Alfred A. Knopf, New York.
- 94. Bennett, C.H. (1973) Logical Reversibility of Computation. IBM Journal of Research and Development, 17, 525-532.
http://dx.doi.org/10.1147/rd.176.0525 - 95. Toffoli, T. (1980) Reversible Computing. CSAIL Publications, Cambridge.
- 96. Hawking, S. (2014) Information Preservation and Weather Forecasting for Black Holes. arXiv:1401.5761 [hep-th]
- 97. Zhang, W.-R. (2012) Beyond Spacetime Geometry—The Death of Philosophy and Its Quantum Reincarnation. Journal of Modern Physics, 3, 1272-1284.
http://dx.doi.org/10.4236/jmp.2012.329164 - 98. Smolin, L. (2005) The Case for Background Independence. arXiv:hep-th/0507235v1
- 99. Lukasiewicz, J. (1920) O logice trojwartosciowej. Ruch Filozoficny, 5, 170-171.
- 100. Zadeh, L. (1965) Fuzzy Sets. Information and Control, 8, 338-353.
http://dx.doi.org/10.1016/S0019-9958(65)90241-X - 101. Brouwer, L.E. (1912) Intuitionism and Formalism. [Dresden, A., English Trans. (1913) Bulletin of the American Mathematical Society, 20, 81-96.]
- 102. Belnap, N. (1977) A Useful 4-Valued Logic. In: Epstein, G. and Dunn, J.M., Eds., Modern Uses of Multiple-Valued Logic, Reidel, 8-37.
- 103. Birkhoff, G. and von Neumann, J. (1936) The Logic of Quantum Mechanics. Annals of Mathematics, 37, 823-843.
http://dx.doi.org/10.2307/1968621 - 104. Hilbert, D. (1901) Mathematical Problems. Bulletin of the American Mathematical Society, 8, 437-479.
http://dx.doi.org/10.1090/S0002-9904-1902-00923-3 - 105. Zhang, W.-R. and Peace, K.E. (2013) Revealing the Ubiquitous Effects of Quantum Entanglement—Toward a Notion of God Logic. Journal of Quantum Information Science, 3, 143-153.
http://dx.doi.org/10.4236/jqis.2013.34019 - 106. Godel, K. (1931) Uber formal unentscheidbare Satze der Principia Mathematica und verwandter Systeme, I. Monatshefte fur Mathematik und Physik, 38, 173-198.
http://dx.doi.org/10.1007/BF01700692 - 107. Rucker, R. (1987) Mind Tools—The Five Levels of Mathematical Reality. Houghton Mifflin, Boston.
- 108. Engel, G.S., Calhoun, T.R., Read, E.L., Ahn, T.-K., Mancal, T., Cheng, Y.-C. and Blankenship, R.E. (2007) Evidence for Wavelike Energy Transfer through Quantum Coherence in Photosynthetic Systems. Nature, 446, 782-786.
http://dx.doi.org/10.1038/nature05678 - 109. Busemeyer, J.R. and Bruza, P.D. (2012) Quantum Models of Cognition and Decision. Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/CBO9780511997716





