Received 15 July 2014; revised 18 August 2014; accepted 4 September 2014

ABSTRACT

Entanglement of tripartite spin states under Lorentz transformations is studied in the context of Bell’s inequality and positive partial transpose criterion. First the relativistic analogue of Bell’s inequality is discussed for three qubit states by explicit calculation of the Wigner rotation. We use the relativistic invariant spin operator which is related to the Pauli-Lubanski pseudo vector. For observers at rest the Bell’s inequality is speed-independent and maximally violated. For moving observers it’s shown that Bell’s inequality is violated and the amount of violation depends on the boost speed. We show that in ultrarelativistic limit Bell’s inequality is still maximally violated. We also obtained the critical value for satisfying Bell’s inequality. The critical value of boost speed for violation of inequality for particles moving in the center of mass frame is greater than that for particles moving with the same momentum. Second we investigate the entanglement distillability of tripartite mixed spin states under Lorentz transformations in the context of Werner states. We show that there are states that will change from distillable (entangled) into separable for a certain value of rapidity.

Keywords:

Wigner Rotation, Bell’s Inequality, Tripartite Entanglement

1. Introduction

Relativistic entanglement and quantum nonlocality are investigated by many authors [1] - [32] . Lorentz boosts entangle the spin and momentum degrees of freedom, so the entanglement between the spins changes if viewed from a moving frame. M. Czachor [7] , investigated Einstein-Podolsky-Rosen experiments with relativistic massive spin-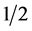 particles. The degree of violation of the Bell’s inequality is shown to depend on the velocity of the pair of spin particles with respect to the laboratory. He considered the spin singlet of two spin- 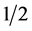massive particles moving in the same direction. He introduced the concept of a relativistic spin observable: which is closely related to the spatial components of the Pauli? Lubanski vector. For two observers in the lab frame measuring the spin component of each particle in the same direction, the expectation value of the joint spin measurement, i.e., the expectation value of the tensor product of the relativistic spin observable of each constituent particle, depends on the boost velocity. Only when the boost speed reaches that of light, or when the direction of the spin measurements is perpendicular to the boost direction, the results seem to agree with the EPR correlation. Czachor considered only the changes in the spin operator part by defining a new relativistic spin operator. There, the state does not need to be transformed since the observer is at rest.

Alsing and Milburn [2] studied the Lorentz transformation of maximally entangled states. By explicit calculation of the Wigner rotation they described the observation of the entangled Bell states from two inertial frames moving with the constant velocity with respect to each other. They concluded that entanglement is Lorentz invariant. Terashima, et al. [30] [31] considered relativistic Einstein-Podolsky-Rosen correlation and Bell’s inequality. They showed that the degree of the violation of Bell’s inequality decreases with increasing the velocity of the observers if the directions of the measurement are fixed. They extended these considerations to the massless case. Ahn, et al. [1] [17] investigated the Bell observable for entangled states in the rest frame seen by the moving observer and showed that the entangled states satisfy the Bell’s inequality when the boost speed approaches the speed of light. In this paper we would like to study the tripartite entanglement in relativistic regime.

The outline of the paper is as follows. In Section 2 we present a brief discussion on the Bell’s inequality for three qubit states. In Section 3 we calculate the Lorentz transformation of three-qubit states. After that we derive the relativistic spin joint measurement of transformed state. Then we derive the expectation value for three-qubit GHZ and W states and calculate the Bell observable for these states. In Section 4 we consider the particles with Gaussian momentum distributions and investigate the distillability of entanglement using the Werner states. We conclude with a discussion in Section 5.

2. Bell’s Inequality

Bell demonstrated that no local and realistic theory could ever agree with all predictions of quantum mechanics [33] . His theorem showed that the idea of completing quantum mechanics, so that the resulting theory would be deterministic, is impossible [34] . Bell’s type inequality for tripartite systems are constructed from correlation function

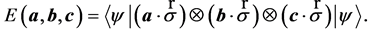(1)

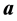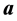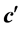here, and are real three-dimensional vectors of unit length. For each measurement, one of two possible alternative measurement is performed: or for particle 1, or for particle 2, or for particle 3. One form of the inequality which is proposed by Mermin is [35]

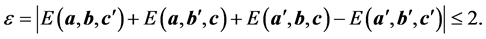(2)

Two fundamental classes of three qubit states which violates the Bell’s inequality are Greenberger-Horne- Zeilinger (GHZ) and W states

(3)

(4)

here 0 and 1 represent the spins polarized up and down along the z-axis. The GHZ and W states are fully symmetric, i.e. invariant under the exchange of any two qubits, and greatly differ each other in their correlations properties.

For a GHZ state if measurements are made in the xy-plane the correlation function to be

(5)

where we labeled the angles from the x-axis. The correlation function can take the value either +1 or −1 under both realistic theory and quantum mechanical theory, thus the maximum value of is 4. For example with the following suitably chosen measurement settings,

(6)

Bell’s inequality for GHZ state is maximally violated with. For W state with measurement in xz-plane we have

(7)

where the polar angle specifies the measurement direction of the spin observable, etc. With the following suitably chosen measurement settings,

(8)

we have.

3. Relativistic Entanglement of Quantum States and Bell’s Inequality

We consider three-particle states described by state vectors made from where is a product state vector of length 1, that represents a state for the momenta of the three particles composed of a state where the momentum of particle is concentrated around a value and etc., and spins represents a state for the spins of the three particles.

We assume that three particles move with the same momentums, for example in x-direction, then the GHZ and W-states are written as

(9)

(10)

For calculation of Bell observable, we use the relativistic spin operator defined by M. Czachor [7]

(11)

where the subscripts and denote the components which are perpendicular and parallel to the boost direction. First we define

(12)

(13)

Effects of relativistic spin observable on three-qubit states is presented in Appendix B, using them we obtain the expectation value of as follows

(14)

One can easily show that the expectation value (14) for set vectors (6) is boost independent and the inequality is maximally violated. For state we have

(15)

Similar to GHZ state the inequality is violated as non relativistic case. The Bell values for GHZ and W states are invariant because the states (9) and (10) are seen by observers at rest. If observers move with velocity respect to particles we should Lorentz transform these states. So we considered the effect of Wigner rotation on the GHZ and W states. For applying Lorentz transformation on states we express GHZ and W states using creation operator in the rest frame

(16)

(17)

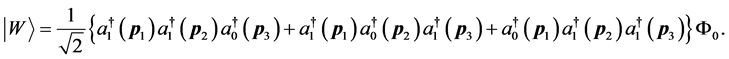
where is Lorentz invariant vacuum state. We consider the case in which the boost speed is perpendicular to momentums of particles. In our case particles move in zy-plane and observers move in x-direction. A Lorentz transformation changes each to then

(18)

which describes momenta concentrated around the Lorentz transformed values and. This is the unitary transformation on the space of momentum states that would represent the Lorentz transformation if the particles had no spins. The Lorentz transformation changes the state vector for momenta and spins as follows

(19)

where and are operators on the spin states for particles, and, respectively, and means.

Now we calculate the Lorentz transformation of GHZ and W states. First we introduce the general pure state of three qubits:

(20)

where

Using relations in Appendix A, Lorentz transformation of GHZ state becomes with

(21)

where is Wigner representation for particle. In a similar manner for W state we have where

(22)

We obtain the degree of violation for two cases.

Cass I.

In this case Wigner representations of the the Lorentz group for particles are written by

(23)

where wigner rotation is defined in Appendix A, relations (140) and (141). Then for GHZ state we have

and for W state

Case II.

We assume particles are emitted in a plane in a configuration in which the three momenta lie at angles of to each other. In this situation particles are in the center of mass frame with the following momentums

(24)

(25)

(26)

therefore

(27)

(28)

(29)

Wigner representations of the the Lorentz group for particles 1, 2 and 3 respectively are written by

(30)

(31)

In this situation for GHZ state coefficients are

(32)

and for W state

(33)

Now the spin joint measurement for the state for measurement in xy plane is given by

(34)

In ultra relativistic limit as we get

(35)

which is not correlated. In non-relativistic limit

(36)

here we consider to the vector set inducing the maximal violation of Bell’s inequality for GHZ state in non relativistic case. With set vector (6) we have

Then for GHZ and W state we have

(37)

(38)

For case I the Bell observable for GHZ state takes the form

(39)

In ultrarelativistic limit as, (39) reduces to

(40)

In this limit amount of violation for very high energy particles goes to zero, but for low energy particles approaches to 4, similar to non-relativistic limit. When particles are in the center of mass frame (case II) Bell observable for GHZ state to be

(41)

which for ultrarelativistic limit as reduces to

(42)

For very high energy particles amount of violation is, but for low energy particles which is maximally violation of Bell’s inequality. In order function of for ultrarelativistic particles

(43)

(44)

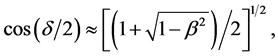
then the amount of violation takes the form

(45)

It’s obvious that critical value for satisfying Bell’s inequality in case I is 0.8, and in case II is 0.97. For W state and case I we arrive at

(46)

Using relations (144) and (145) takes the form

(47)

In ultrarelativistic limit as reduces to

(48)

For low energy particles amount of violation goes to zero and for high energy particles. It is interesting that in non-relativistic case. One can obtain the critical value for boost speed when particles are high energitic. In this limit, then. For measurement in xz-plane we have

(49)

with the set of vectors (8) we obtain

For W state in the case I the Bell observable reads

(50)

It’s obvious that in relativistic domain Bell’s inequality is violated for W states. Bell observable in order function of for ultrarelativistic particles takes the form

(51)

The critical value for violation of inequality is, which is smaller than GHZ state case. For case II we have

(52)

For ultrarelativistic particles the critical value is 0.73.

Finally we consider the case in which the momentums and boost are not in the same plane. In this case Wigner matrices takes the form

(53)

with

(54)

(55)

and

(56)

(57)

(58)

Assume that three particles move with the momentums. Then the Bell observable for state to be

(59)

which in nonrelativistic limit gives the value 4.

4. Distillability of Entanglement

In the previous section for simplicity we assumed that momentum of particles are sufficiently localized around momentum. Realistic situation involve the wave pockets with Gaussian form. In this section we consider the specific situation in which Alice (A), Bob (B) and Charlie (C) share a tripartite mixed state which is mixture of Greenberger-Horne-Zeilinger (GHZ) state with identity, with respect to an inertial frame. Moreover, in order realize the effects of relativity on distillability, we also consider another inertial frame, where relatives, and of, and are moving with relative velocity, with respect to. For a composite system of three qubits one can consider the Werner state [36]

(60)

or in the matrix form

(61)

The basis is. To determine whether or not this state is entangled we use the partial transpose criterion [37] . We say a density matrix has a positive partial transpose if its partial transposition has no negative eigenvalues. The eigenvalues of partial transpose of density matrix are

(62)

(63)

Then the state to be entangled for and separable for. The state is made up of three par-

ticles, say electrons with mass, having two types of degrees of freedom: momentum and spin. The former is a continuous variable while the latter is a discrete one. Each particle is assumed to be localized, as in a box, and its momentum will be described by the same Gaussian distribution. Then the state is

(64)

where, and are the corresponding momentums vectors of particles, and and

(65)

(66)

(67)

with Gaussian momentum distributions

(68)

If we trace the momentum degrees of freedom we obtain the usual state. The general density matrix for three particle systems with momentums and is given by

(69)

In our case the coefficients are

(70)

(71)

(72)

For obtaining the Lorentz transformation of density matrix (69), we need the relativistic properties of spin entropy for a single, free particle of spin-1/2. The quantum state of a spin-1/2 particle can be written in the momentum representation as follows

(73)

where

(74)

The density matrix corresponding to state is

(75)

By setting and integrating over we obtain the reduced density matrix for spin

(76)

where the Bloch vector is given by

(77)

(78)

Under the Lorentz transformation the states (65)-(67) transformed as [15]

(79)

(80)

Now under Lorentz boost density matrix (69) transformed into

(81)

The reduced density matrix for spin is obtained by setting, , and tracing over momentum

(82)

To leading order W⁄M« 1 we have [15]

(83)

where and is boost speed. Larger values of are possible and mathematically

correct, though not necessarily physically consistent. The case of would produce fast wave-packet spreading, yielding an undesired particle delocalization. It can be appreciated in Equation (82) that the expression is decomposable in the sum of the tensor products of spin blocks, each corresponding to each particle. We compute now the different blocks, corresponding to the four possible tensor products of the states (79) and (80)

(84)

(85)

(86)

(87)

With the help of Equations (84)-(87), it is possible to compute the effects of the Lorentz transformation, associated with a boost in the x direction, on any density matrix of two spin-1/2 particles with factorized Gaussian momentum distributions. In particular density matrix (81) reduced to

(88)

where

(89)

To determine whether or not this state is entangled we use the partial transpose criterion [37] . We say a density matrix has a positive partial transpose if its partial transposition has no negative eigenvalues. The partial transpose criterion provides a sufficient condition for the existence of entanglement in this case: if at least one eigenvalue of the partial transpose is negative, the density matrix is entangled. The eigenvalues of PT density matrix are

The eigenvalue for always is negative. Then in the interval dis-

tillability of state is possible in rest frame but is impossible in moving frame. Then there are states that will change from distillable (entangled) into separable for a certain value of, showing the relativity of distillability and separability.

5. Summary

In conclusion, we obtained the relativistic spin joint measurements for Lorentz transformed three-qubit states as momentums of particles are perpendicular to the boost speed. We show that in ultrarelativistic limit joint measurements are uncorrelated. Using Bell’s inequality, we studied the nonlocal quantum properties of states in relativistic formalism. Bell’s inequality is maximally violated in rest frame or in moving frame with rest particles, but is not always violated as seen by moving observer, because the degree of violation of Bell’s inequality depends on the velocity of the particles and observer. In non-relativistic case the spin degrees of freedom and momentum degrees of freedom are independent. But in relativistic regime Lorentz transformations of spin of particle depend on its momentum. Lorentz transformations can change the entanglement of the spins of massive particles.

EPR experiment for three qubits is investigated for two cases. In the first case particles move with the same momentum and in the second case particles move in the center of mass frame. Bell’s inequality is maximally violated in relativistic regime. In ultrarelativistic limit inequality is still maximally violated, which is not same as two-qubite case [1] [17] . For W state when measurement performed in xy-plan in ultrarelativistic limit inequality is violated, but in non-relativistic limit reaches to zero. Finally, for very high energy particles we obtained a critical value for satisfying Bell’s inequality. For GHZ and W states critical value for violation of Bell’s inequality when particles move in the center of mass is greater than the case when particles move with the same momentum.

For particles with Gaussian momentum distributions we show that there are states that will change from distillable (entangled) into separable for a certain value of n, showing the relativity of distillability and separability.

References

Appendix A: Wigner Representation of the Poincare Group [38] - [43]

Poincaré transformation is combination of proper Lorentz transformation with space-time translation

(90)

The unitary transformation in the Hilbert space of state vectors corresponding to the Poincaré transformation is given by

(91)

where anti-symmetric tensor is related to generators of boosts and rotations respectively as follows

(92)

and is the anti-symmetric tensor

(93)

Here with is a normal vector in the boost direction. Finally are the generators of space-time translations. The commutation relations between the generators of Poincare group are

(94)

(95)

(96)

The concept of intrinsic spin and angular momentums can be generalized to relativistic situation using the Pauli-Lubanski tensor

(97)

with components

(98)

This tensor satisfies in following relations

(99)

(100)

(101)

From the algebra of the generators one finds that and commute with all generators and therefore are invariants under Poincaré transformation. These operators are Casimir operators of the algebra. Single particle states form the unitary representation of the group of Poincaré transformation. States labelled using of mutually commuting operators. Mass from eigenvalue of, three momentum vector from operator, spin from eigenvalue of operator and polarization or spin projection from eigenvalue of helicity operator

(102)

or z-component in rest frame. The helicity is most continent since it is invariant under rotation and under Lorentz boosts along. Also the helicity of a massless particle is Lorentz invariant. One can show the eigenvalues of is.

(103)

Then we have

(104)

(105)

(106)

For a particle of nonzero mass, one can define intrinsic spin and orbital angular momentum using

(107)

(108)

Note that is Lorentz invariant and that and satisfy the following relations

(109)

(110)

(111)

(112)

(113)

In the rest frame the spin vector is. Actually is the spatial part the vector transformed to the rest frame of. That is

(114)

where is the pure Lorentz transformation which maps the time axis into the direction of the vector

(115)

the explicit form of the matrix is

(116)

(117)

Another candidate for spin operator is based on the center of mass operator defined by

(118)

here denotes finite-dimensional angular momentum matrices corresponding to the -dimensional representation of the rotation group. Then the spin corresponding to is

(119)

The eigenvalues of are therefore

(120)

where and is an arbitrary direction. For the generators of the Lie algebra of three-dimensional Euclidian rotations or the group are pauli matrices. So the normalized operator corresponding to the spin projection along an arbitrary direction is [7]

(121)

where the subscripts and denote the components which are perpendicular and parallel to the boost direction. Operator is related to the Pauli-Lubanski pseudo vector which is relativistic invariant operator corresponding to spin.

Irreducible representation of Poincaré group constructed from irreducible representation of little group which leaves the reference four momentum invariant. The rotation takes the three-vector initially pointing in the z-direction into a three-vector pointing along the direction of associated the four vector. If the direction of is directed by polar angle and an azimuthal angle, then

(122)

The rotation is a sequence of three rotations: first about the z-axes by angle then about the y-axes by angle then again around the z-axes by angle. The Lorentz boost which takes an initially massive state at rest into a state with momentum is

123)

The pure Lorentz boost which takes an initially massive state at rest into a state with momentum is

(124)

Now choose as the reference momentum, then the little group is the ordinary spatial rotations. The states are then constructed as follows

(125)

The normalization factor is chosen to satisfy

(126)

under Poincaré transformation

(127)

where

(128)

The are the conventional -dimensional unitary matrices representing the three-dimensional rotation group. Note that and, hence. Since it leaves invariant should be a pure spatial rotation. It is a member of the little group. In the following discussion, we omit the normalization factors, such as because these do not affect the result of our discussion.

Creation and annihilation operators may be defined in terms of their effect on the normalized multi-particle states. The creation operator is defined as the operator that adds a particle with quantum number

(129)

here labels spin z-components (or helicities, for massless particles). Now the multipartite state is expressed by acting on the vacuum with N creation operators

(130)

where is Lorentz invariant vacuum state. We will need the transformation properties of the creation and annihilation operators. We consider to inhomogeneous proper orthochronous Lorentz transformation propriety [40]

(131)

where is the three vector part of. Transformation of creation operator is

(132)

Outline of derivation of the representation of the Wigners little group for spin-1/2 particles is as follows [43]

(133)

where

(134)

(135)

with

(136)

(137)

here. After some mathematical manipulation

(138)

which can be written in the abbreviated form

(139)

with

(140)

(141)

here,. We consider the case in which the boost speed is perpendicular to momentums of particles. In this case we have

(142)

(143)

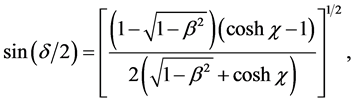
where in ultrarelativistic limit as take the forms

(144)

(145)

Appendix B

Effects of relativistic spin observable with the boost in x-direction on three-qubit states are