Journal of Quantum Information Science
Vol.4 No.2(2014), Article ID:46452,7 pages DOI:10.4236/jqis.2014.42011
Quantum Discord of a Two-Qubit Anisotropy XXZ Heisenberg Chain with Dzyaloshinskii-Moriya Interaction
Nour Zidan
Mathematics Department, Faculty of Science, Sohag University, Sohag, Egypt
Email: nazidan@yahoo.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 6 March 2014; revised 2 May 2014; accepted 22 May 2014
ABSTRACT
We investigate the quantum discord of a two-qubit anisotropy XXZ Heisenberg chain with Dzyaloshinskii-Moriya (DM) interaction under magnetic field. It is shown that the quantum discord highly depends on the system’s temperature T, DM interaction D, homogenous magnetic field B and the anisotropy Δ. For lower temperature T, by modulating D and B, the quantum discord can be controlled and the quantum discord switch can be realized.
Keywords:Quantum Discord, Heisenberg Chain, Dzyaloshinskii-Moriya Interaction, Anisotropy, Magnetic Field

1. Introduction
Quantum discord is a new physical quantity introduced by Henderson and Vedral [1] and (independently) Ollivier and Zurek [2] , which is used to quantify all nonclassical correlation systems [3] . The quantum discord is defined as the difference between quantum mutual information and classical correlation in a bipartite system [4] [5] . The calculations of quantum discord require minimization procedures, so the quantum discord is somewhat difficult to calculate and one cannot get the analytical solutions. It had been calculated explicitly only for a rather limited set of two-qubit quantum states and expressions for more general quantum states are still not known. However, for a family of two-qubit states, the quantum discord has been evaluated and analytical formulas have been obtained [6] . The explicit expressions for quantum discord have been derived for more general quantum states, such as the so-called X states. Quantum discord, entanglement and classic correlation are independent measures of correlations with no simple relative ordering [7] [8] . An extreme example is realized in the search of maximally discordant mixed states. It has revealed that states maximizing the quantum discord for given value of the classical correlations do not maximize the entanglement and are, in some cases, even separable [9] . Very recently, a reliable and effective algorithm for the evaluation of the quantum discord of the general twoqubit states is presented, where the optimization problem for the quantum discord is expressed in a compact form [10] . As is well known, the quantum entanglement of condensed matter systems is an important emerging field. Accordingly, several investigations of entanglement in thermal equilibrium states of spin chains subject to an external magnetic field, at finite temperatures, have been made [11] -[16] . Recently, some interesting works have investigated the thermal quantum discord in various Heisenberg models [17] -[21] . It shows that the thermal quantum discord is more robust than the thermal entanglement against temperature. Because quantum discord does not disappear at finite temperature, but at a certain temperature thermal entanglement completely disappears, so quantum discord is more practical than entanglement to describe quantum correlation. Taking the spin-orbit effect into account, the effect of Dzyaloshinskii-moriya interaction has been investigated by numerous works with various models [22] -[25] .
In this paper, we study the quantum discord in a two-qubit anisotropic XXY Heisenberg chain in thermal equilibrium in presence of a homogenous magnetic field with Dzyaloshinskii-moriya (DM) interaction, and discuss how the temperature T, DM interaction D, homogenous magnetic field B and the anisotropy Δ influence the quantum discord in such system. This paper is organized as follows: In Section 2, the Hamiltonian of the system is introduced and expression of quantum discord is given. In Section 3, numerical results are discussed. Finally, we conclude in Section 4.
2. Model and Its Quantum Discord
The Hamiltonian for a two-qubit Heisenberg XXZ chain in the presence of an external magnetic field and Dzyaloshinskii-Moriya (DM) interaction can be written as [26]
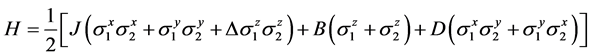 , (1)
, (1)
where,  are the vector of Pauli matrices, J is the coupling parameter between the nearest neighbor site, B is a homogenous magnetic field and D is the DM interaction which assumed to be along the z-direction. Also Δ is a dimensionless parameter characterizing the anisotropy of the model. For a system in thermal equilibrium at temperature T, the density operator can be written as
are the vector of Pauli matrices, J is the coupling parameter between the nearest neighbor site, B is a homogenous magnetic field and D is the DM interaction which assumed to be along the z-direction. Also Δ is a dimensionless parameter characterizing the anisotropy of the model. For a system in thermal equilibrium at temperature T, the density operator can be written as ![]() with
with 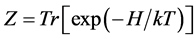 being the partition function and k being Boltzmann’s constant (for simplicity one set k=1). In the representation with basis states
being the partition function and k being Boltzmann’s constant (for simplicity one set k=1). In the representation with basis states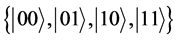 , the density operator for the system under consideration in thermal equilibrium can be worked out to be
, the density operator for the system under consideration in thermal equilibrium can be worked out to be
 (2)
(2)
with
 (3.1)
(3.1)
 (3.2)
(3.2)
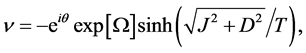 (3.3)
(3.3)
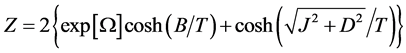 (3.4)
(3.4)
where, ![]() and
and 
After the dynamical model under consideration has been introduced, we turn our attention to obtain an analytic expression of quantum discord. However, for the X state described by the density matrix
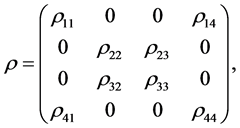 (4)
(4)
quantum discord (QD) is given as [8]
![]() (5)
(5)
with

and
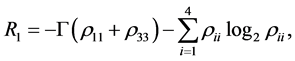

where  being the four eigenvalues of the density matrix
being the four eigenvalues of the density matrix 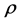 and
and ![]()
As the density matrix of our system ρ in Equation (2) is X states, quantum discord can be evaluated by substituting from Equation (2) into Equation (5) after straightforward calculation, quantum discord reads
![]() (6)
(6)
with

and

where 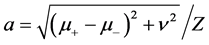
3. Discussion
In the following study, we are going to use the obtaining results in the previous section to illustrate the effect of the temperature T, DM interaction D, homogenous magnetic field B and the anisotropy parameter Δ on the quantum discord numerically. In Figure 1, the quantum discord is plotted as a function of the thermal equilibrium temperature T and homogenous magnetic field B. It is shown that the decay of quantum discord occurs when the temperature T is increased. On the other hand, as DM interaction D is increased the quantum discord is increased and large amount of quantum discord can be obtained, as well as when B is increased the quantum discord is decreased, but with larger values of D the decreasing rate is smaller. Now we check the effect of homogenous magnetic field B on quantum discord. The quantum discord as a function of magnetic field B is plotted in Figure 2. It is interesting to see that the quantum discord is symmetrical about B. Moreover, by the contrast on Figure 2(a) and Figure 2(b), one find that the more (DM) interaction D will result in wider quantum discord and the longlived maximum discord is more pronounced. Also as T is increased the local maximum of the quantum discord is
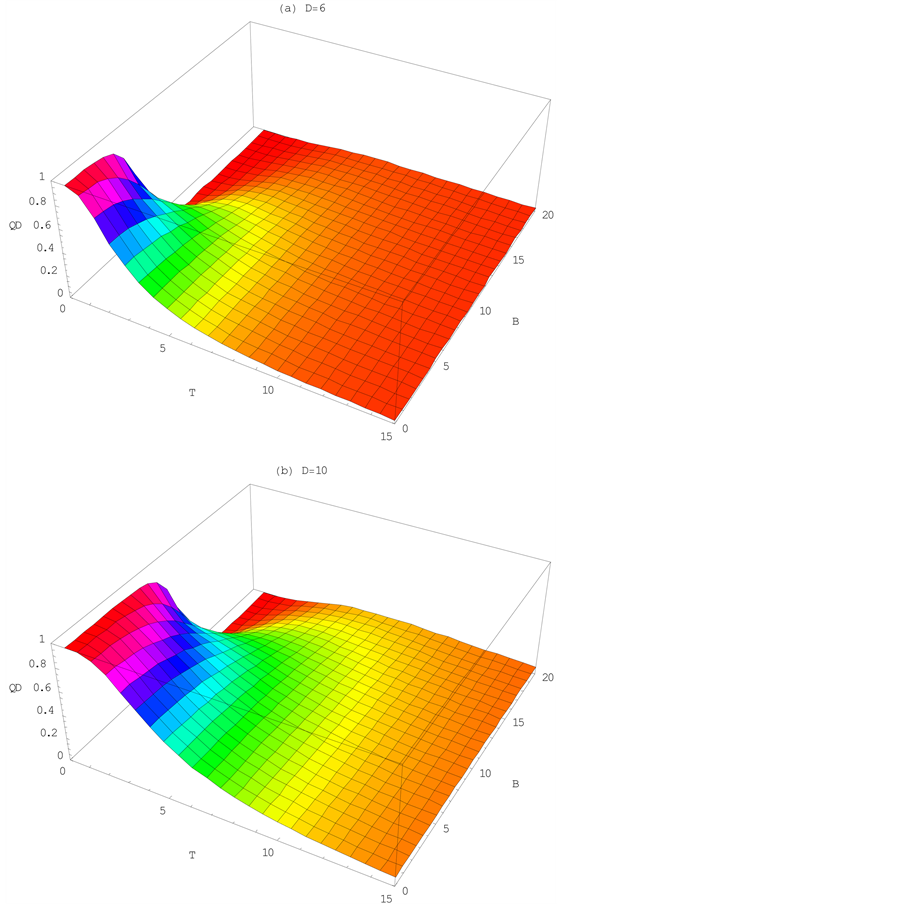
Figure 1. Quantum discord (QD) versus temperature T and magnetic field B for different values of D with Δ = 0.5 and J = 1.

Figure 2. Quantum discord (QD) versus magnetic field B at different values of T and D with Δ = 0.2 and J = 1. Solid black, dashed red, dotted blue curves represent T = 0.5, T = 1, T = 1.5 respectively.
decreased. In Figure 3, the influence of Dzyaloshinskii-Moriya interaction D on quantum discord is numerically considered. By the comparison among Figure 2 and Figure 3, one find it is different that realizing quantum discord by adjusting B from adjusting D. The former can make the quantum discord converted from zero to a fixed value then to zero whereas the latter make quantum discord converted from zero to a fixed value. Obviously, it is easier to realize the continuous change of homogenous magnetic field B than the continuous change of (DM) interaction D, so it is more practical realizing quantum discord by modeling homogenous magnetic field B. The size dependence of quantum discord for anisotropy parameter Δ is plotted in Figure 4. One can see for the quantum-
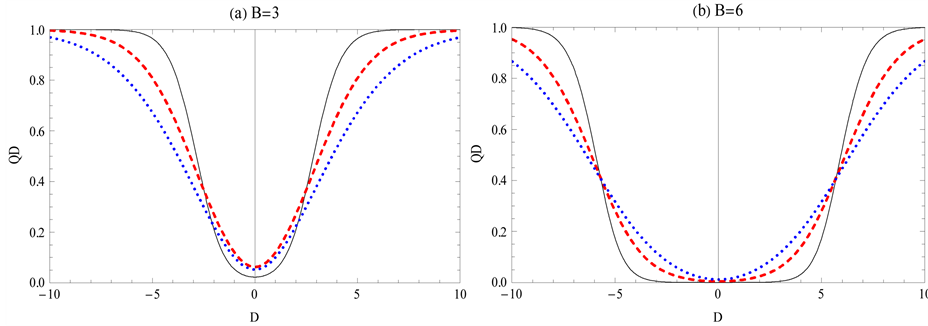
Figure 3. Quantum discord (QD) versus DM interaction D at different values of T and B with Δ = 0.2 and J = 1. Solid black, dashed red, dotted blue curves represent T = 0.5, T = 1, T = 1.5 respectively.

Figure 4. Quantum discord (QD) versus anisotropy Δ at different values of T, B and D with J = 1. Solid black, dashed red, dotted blue curves represent T = 0.5, T = 1, T = 1.5 respectively.
discord there exists a critical anisotropy Δc , when the system’s anisotropy exceeds the critical value the quantumdiscord tends to local maximum value. The results enable us to conclude that the anisotropy critical value depends entirely on the values of each of B and D when B equal D, the critical value is equal to zero, and if B greater than D the critical value is a positive value and finally if B less than D the critical value is a negative value.
4. Conclusion
In this paper, we have studied the quantum discord of a two-qubit anisotropy XXZ Heisenberg chain under Dzyaloshinskii-Moriya (DM) interaction and homogeneous magnetic field. Our study shows that the quantum discord decreases asymptotically to zero when temperature T increases. For low temperature, the quantum discord is found and it is closely related to Dzyaloshinskii-Moriya (DM) interaction D and homogeneous magnetic field B. By controlling the values of D and B, one can change the phase transition points. As well as, for the anisotropy parameter Δ, there exists critical anisotropy Δc. When the system’s anisotropy exceeds the critical value, the quantum discord tends to local maximum value.
References
- Henderson, L. and Vedral, V. (2001) Classical, Quantum and Total Correlations. Journal of Physics A: Mathematical and General, 34, 6899. http://dx.doi.org/10.1088/0305-4470/34/35/315
- Ollivier, H. and Zurek, W.H. (2001) Quantum Discord: A Measure of the Quantumness of Correlations. Physical Review Letters, 88, Article ID: 017901. http://dx.doi.org/10.1103/PhysRevLett.88.017901
- Lanyon, B.P., Barbieri, M., Almeida, M.P. and White, A.G. (2008) Experimental Quantum Computing without Entanglement. Physical Review Letters, 101, Article ID: 200501. http://dx.doi.org/10.1103/PhysRevLett.101.200501
- Knill, E. and Laflamme, R. (1998) Power of One Bit of Quantum Information. Physical Review Letters, 81, Article ID: 5672. http://dx.doi.org/10.1103/PhysRevLett. 81.5672
- Guhne, O. and Toth, G. (2009) Entanglement detection. Physics Reports, 474, 1-75. http://dx.doi.org/10.1016/j.physrep.2009.02.004
- Luo, S. (2008) Quantum Discord for Two-Qubit Systems. Physical. Review A, 77, Article ID: 042303. http://dx.doi.org/10.1103/PhysRevA.77.042303
- Ali, M. and Rau, A.R.P. and Alber G. (2010) Quantum Discord for Two-Qubit X States. Physical Review A, 81, Article ID: 042105. http://dx.doi.org/10.1103/PhysRevA.81.042105
- Wang, C.-Z., Li, C.-X., Nie, L.-Y. and Li, J.-F. (2011) Classical Correlation and Quantum Discord Mediated by Cavity in Two Coupled Qubits. Journal of Physics B: Atomic, Molecular and Optical Physics, 44, Article ID: 015503. http://dx.doi.org/10.1088/0953-4075/44/1/015503
- Galve, F., Giorgi, G.L. and Zambrini, R. (2011) Maximally Discordant Mixed States of Two Qubits. Physical Review A, 83, Article ID: 012102. http://dx.doi.org/10.1103/PhysRevA.83.012102
- Girolami, D. and Adesso, G. (2011) Quantum Discord for General Two-Qubit States: Analytical Progress. Physical Review A, 83, Article ID: 052108. http://dx.doi.org/10.1103/PhysRevA.83.052108
- Arnesen, M.C., Bose, S. and Vedral, V. (2001) Natural Thermal and Magnetic Entanglement in the 1D Heisenberg Model. Physical Review Letters, 87, Article ID: 017901. http://dx.doi.org/10.1103/PhysRevLett. 87.017901
- Wang, X. (2001) Entanglement in the Quantum Heisenberg XY Model. Physical. Review A, 64, Article ID: 012313. http://dx.doi.org/10.1103/PhysRevA.64.012313
- Zhou, L., Song, H.S. Guo, Y.Q. and Li, C. (2003) Enhanced Thermal Entanglement in an Anisotropic Heisenberg XYZ Chain. Physical. Review A, 68, Article ID: 024301. http://dx.doi.org/10.1103/PhysRevA.68.024301
- Rigolin, G. (2004) Thermal Entanglement in the Two-Qubit Heisenberg XYZ Model. International Journal of Quantum Information, 2, 393. http://dx.doi.org/10.1142/S0219749904000262
- Zhang, G.-F. and Li, S.-S. (2005) Thermal Entanglement in a Two-Qubit Heisenberg XXZ Spin Chain under an Inhomogeneous Magnetic Field. Physical. Review A, 72, Article ID: 034302. http://dx.doi.org/10.1103/PhysRevA.72.034302
- Kheirandish, F., Akhtarshenas, S.J. and Mohammadi, H. (2008) Effect of Spin-Orbit Interaction on Entanglement of Two-Qubit Heisenberg XYZ Systems in An Inhomogeneous Magnetic Field. Physical. Review A, 77, Article ID: 042309. http://dx.doi.org/10.1103/PhysRevA.77.042309
- Werlang, T. and Rigolin, G. (2010) Thermal and Magnetic Quantum Discord in Heisenberg Models. Physical. Review A, 81, Article ID: 044101. http://dx.doi.org/10.1103/PhysRevA.81.044101
- Werlang, T. and Trippe, C., Ribeiro, G.A.P. and Rigolin, G. (2010) Quantum Correlations in Spin Chains at Finite Temperatures and Quantum Phase Transitions. Physical Review Letters, 105, Article ID: 095702. http://dx.doi.org/10.1103/PhysRevA.81.044101
- Guo, J.-L., Li, Z.-D. and Sun, Y.-B. (2011) Pairwise Entanglement in the Heisenberg XX model with Three-Site Interactions. Optics Communications, 284, 1461-1467. http://dx.doi.org/10.1016/j.optcom.2010.10.089
- Guo, J.-L., Mi, Y.-J., Zhang J. and Song, H.-S. (2011) Thermal Quantum Discord of Spins in an Inhomogeneous Magnetic Field. Journal of Physics B: Atomic, Molecular and Optical Physics, 44, Article ID: 065504. http://dx.doi.org/10.1088/0953-4075/44/6/065504
- Xie, M.-Q. and Guo, B. (2013) Thermal Quantum Discord in Heisenberg XXZ Model under Different Magnetic Field Conditions. Acta. Physica Sinica, 62, Article ID: 110303. http://dx.doi.org/10.7498/aps.62.110303
- Zhu, Y.Y. and Zhang, Y. (2012) Quantum Discord in the Three-Spin XXZ Chain with Dzyaloshinskii-Moriya Interaction. SCIENCE CHINA Physics, Mechanics & Astronomy, 55, 2081-2087. http://dx.doi.org/10.1007/s11433-012-4871-x
- Tursun, M., Abliz, A., Mamtimin, R., Abliz, A. and Qiao, P.-P. (2013) Various Correlations in the Anisotropic Heisenberg XYZ Model with Dzyaloshinski—Moriya Interaction. Chinese. Physics. Letters. 30, Article ID: 030303. http://dx.doi.org/10.1088/0256-307X/30/3/030303
- Vahedi, J., Soltani, M.R. and Mahdavifar M.R. (2014) Quantum Correlation in Three-Qubit Ising Model with Added Dzyaloshinskii-Moriya Interaction. Journal of Superconductivity and Novel Magnetism. http://dx.doi.org/10.1007/s10948-014-2498-z
- Xu, S., Song, X.-K. and Ye, L. (2014) Measurement-Induced Disturbance and Negativity in Mixed-Spin XXZ Model. Quantum Information Process, 13, 1013-1024. http://dx.doi.org/10.1007/s11128-013-0706-6
- Qlan, L., and Fang, J.-X. (2009) Thermal Entanglement of a Two-Qubit XXZ Heisenberg Chain with Dzyaloshinskii-Moriya Interaction. Communications in Theoretical Physics, 52, 817. http://dx.doi.org/10.1088/0253-6102/52/5/10

