Journal of Quantum Information Science
Vol.4 No.1(2014), Article ID:43551,10 pages DOI:10.4236/jqis.2014.41004
Entanglement Quantifier Based on Atomic Wehrl Entropy for Non-Linear Interaction between a Single Two-Level Atom and SU(1,1) Quantum System
Sayed Abdel-Khalek, Manal Al-Quthami, Mohamed M. A. Ahmed
Mathematics Department, Faculty of Science, Taif University, Taif, KSA
Email: mabdel_K@ictp.it
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 11 November 2013; revised 11 January 2014; accepted 28 February 2014
ABSTRACT
In this paper, we study the dynamics of the atomic inversion, scaled atomic Wehrl entropy and marginal atomic Wehrl density for a single two-level atom interacting with SU(1,1) quantum system. We obtain the expectation values of the atomic variables using specific initial conditions. We examine the effects of different parameters on the scaled atomic Wehrl entropy and marginal atomic Wehrl density. We observe an interesting monotonic relation between the different physical quantities for different values of the initial atomic position and detuning parameter.
Keywords:Scaled Atomic Wehrl Entropy; Atomic Q-Function; Atomic Inversion

1. Introduction
Quantum entropy, is considered the main generalization of the Boltzmann classical entropy, proposed by von Neumann [1] . It has been applied, as a measure to many aspects in quantum information processing such as quantum entanglement, photocount statistics, quantum decoherence, quantum optical correlations, purity of the quantum states, accessible information in quantum measurement. The quantification of entanglement is necessary to understand and develop the quantum information theory. For this reason different entanglement measures have been used for the mixed and pure states such as concurrence [2] -[5] , entanglement of formation [6] [7] , and negativity [2] [3] . In this way, the concurrence and negativity are used as a good entanglement measure for mixed state, but the von Neumann entropy has been proposed for pure state entanglement [1] , all these measures to test whether a given quantum state is separable or entangled. Also, some interesting physical phenomenon is observed as a result of entanglement measure, such as “entanglement sudden death” (ESD), entanglement sudden birth (ESB) [8] -[14] .
The Wehrl entropy (WE) is more sensitive in distinguishing states than the von Neumann entropy since WE is a state dependent [15] . The concept of the Wehrl phase distribution (WPD) has been developed and shown that it serves as a measure of both noise (phase-space uncertainty) and phase randomization [16] . Furthermore, the WE has been applied to some dynamical systems, too. In this respect, the time evolution of the field WE for the Kerr-like medium has been discussed in [17] [18] showing that the FWE gives a clear signature for the formation of finite superposition of coherent states (cat-like states) as well as the number of coherent components taking part in the superposition. For the trapped ion system the WE gives an information on the dynamical properties and entanglement of the system [19] [20] . On the other hand some features of WE and WPD of a singleCooper pair box placed inside a dissipative cavity have been discussed [21] . It is shown that phase damping leads to generating long living correlation of the system.
Different entanglement measures and quantifiers for mixed and pure states have been proposed, such as the negativity and atomic Wehrl entropy. The relation between mixed state entanglement and the atomic Wehrl entropy (AWE) has not been studied widely. However, there are some attempts to quantify the pure state entanglement by using AWE. In this context, the entanglement evaluation with AWE and atomic Fisher information has been investigated [22] [23] . It has been found that entanglement of a two-level atom can be measured by AWE and their marginal distribution. On the other hand, atomic Wehrl entropy was used as an entanglement measure for a mixed state two-level system in the presence of intrinsic decoherence [24] . It found that the information about entanglement is obtained by comparing the results for the atomic Wehrl entropy and negativity with the analytical results for a simple case.
Realistic quantum systems are not closed, which causes the rapid destruction of crucial quantum properties. Therefore, the unavoidable interaction between a quantum system, understanding the dynamics of entanglement measures and finding the correlation between different phenomenons may stimulate great interest. In the present article, our main interest is to investigate the evolution of the scaled atomic Wehrl entropy (AWE) of a single two-level atom and SU(1,1) quantum system in the presence of detuning parameter, which leads us to address the question: Can the AWE be used as a indicator of the entanglement and dynamical properties of the system in the presence of non-linear terms?
The article is organized as follows: In Section 2, we introduce the model of the single two-level and SU(1,1) quantum system in the presence of detuning parameter. The definitions of the scaled atomic Wehrl entropy, atomic inversion and marginal atomic Wehrl density are introduced in Section 3. We conclude the main results with some remarks in Section 4.
2. The System Hamiltonian
The Hamiltonian which describe the interaction between a single two-level atom and 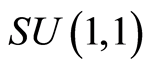 quantum system take the following form
quantum system take the following form
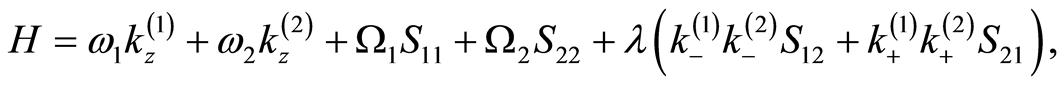 (1)
(1)
where  is the frequency of the system,
is the frequency of the system,  is the energy and
is the energy and 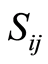 are elements of the
are elements of the 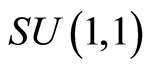 group obeying the following commutation relation
group obeying the following commutation relation
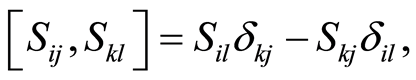 (2)
(2)
while 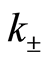 and
and  satisfy the following commutation relation
satisfy the following commutation relation
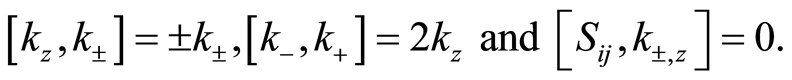 (3)
(3)
The Heisenberg equation of motion for any operator 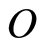 is given by
is given by
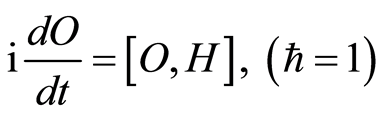 (4)
(4)
thus, the equations of motion for  and
and 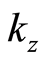 are given by
are given by
 (5)
(5)
 (6)
(6)
 (7)
(7)
 (8)
(8)
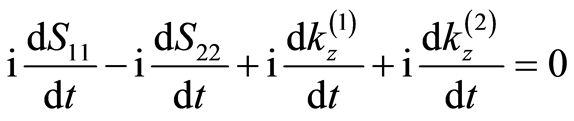 (9)
(9)
then
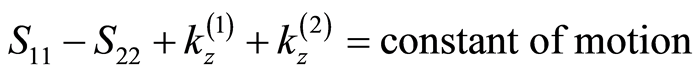
In this case, we have ,
, 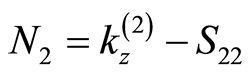 are constant of motion. Therefore, the Hamiltonian takes the following form
are constant of motion. Therefore, the Hamiltonian takes the following form
 (10)
(10)
where 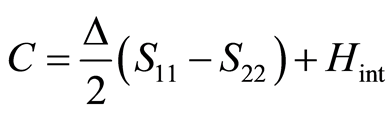 with
with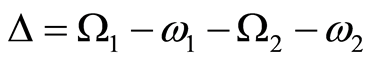 . We note that
. We note that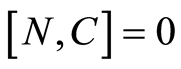 , therefore
, therefore 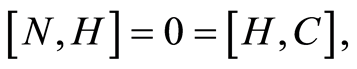 i.e.
i.e. 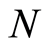 and
and 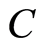 are constants of motion, where
are constants of motion, where 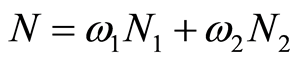 the time evolution operator is defined
the time evolution operator is defined
 (11)
(11)
thus
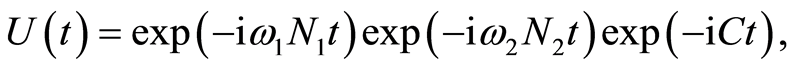 (12)
(12)
where
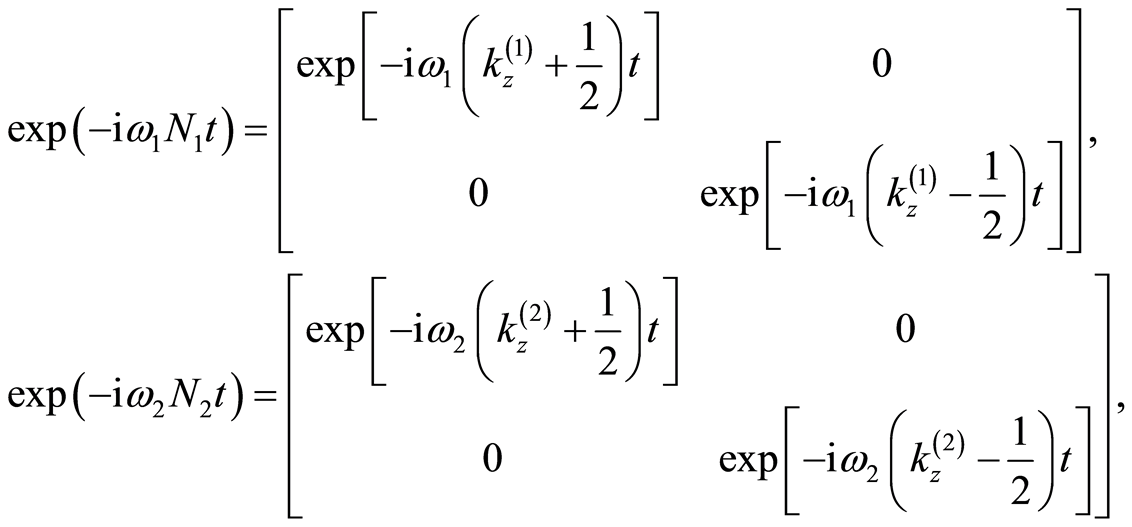 (13)
(13)
 (14)
(14)
 (15)
(15)
where
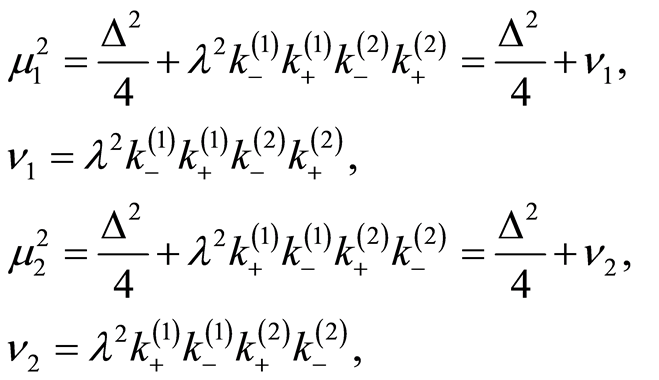 (16)
(16)
we note that
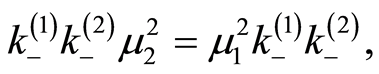 (17)
(17)
also
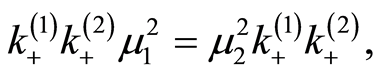 (18)
(18)
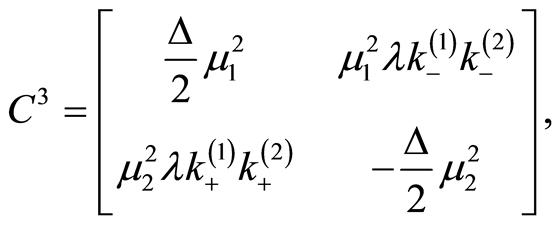 (19)
(19)
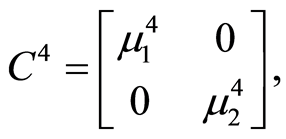 (20)
(20)
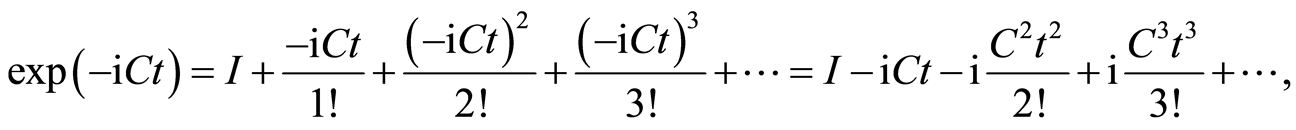 (21)
(21)
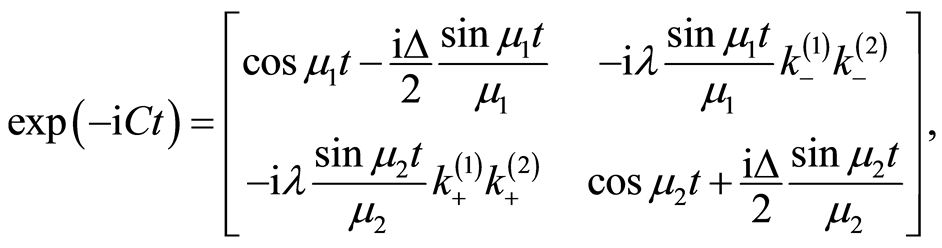 (22)
(22)
for simplicity we can write
 (23)
(23)
where
 (24)
(24)
The time evolution for the expectation value of any operator can be calculate through the following relation
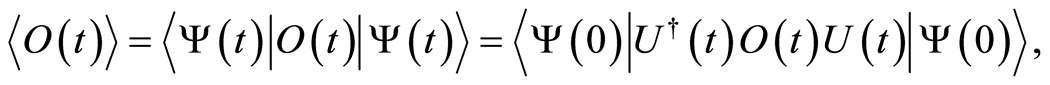 (25)
(25)
Now the initial state of the system can be written as
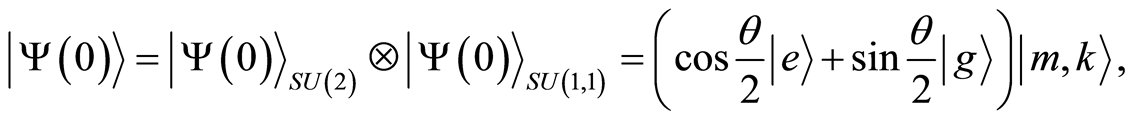 (26)
(26)
where
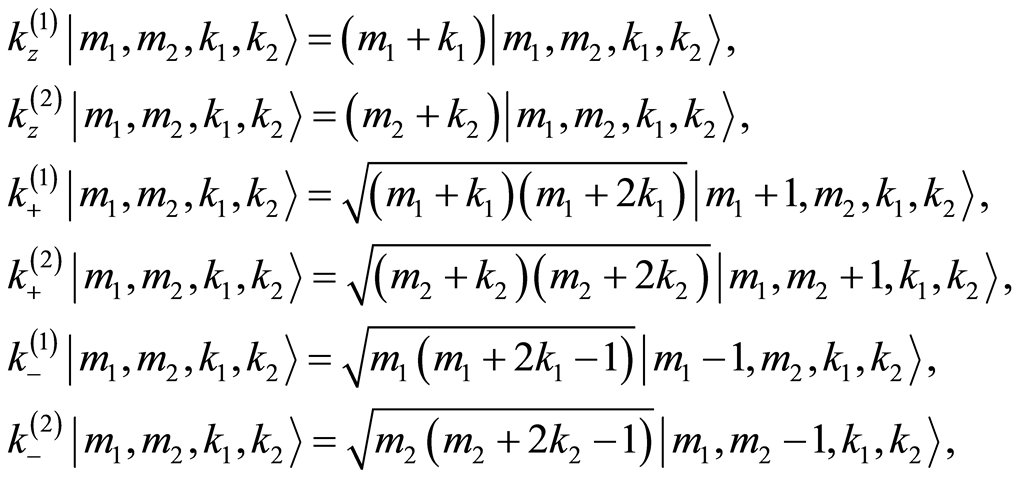 (27)
(27)
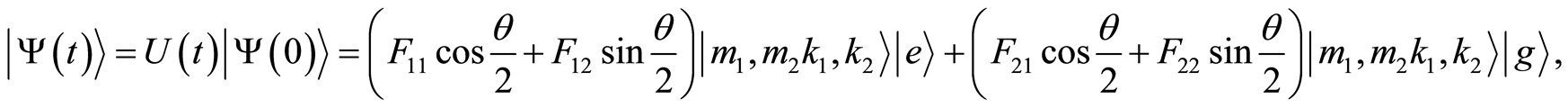 (28)
(28)
Substituting from Equation (26) in Equation (28), then the final form of the wave function can be written as
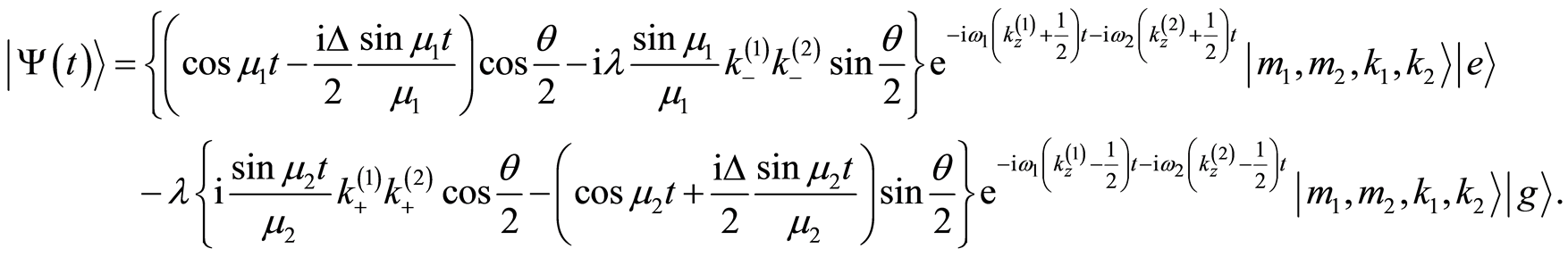 (29)
(29)
Then the wave function can be written in the form
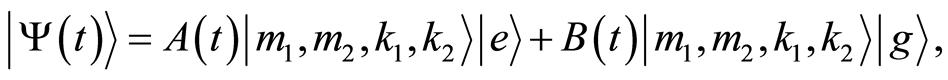 (30)
(30)
and consequently the density matrix 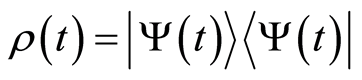 becomes
becomes
 (31)
(31)
where
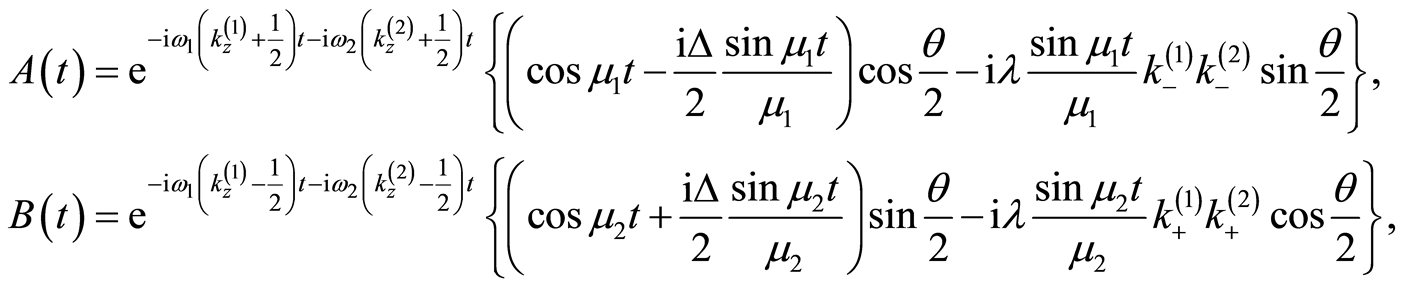 (32)
(32)
and
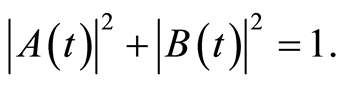 (33)
(33)
Thus the expectation value for any operator can be calculated through
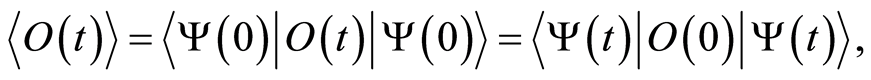 (34)
(34)
where 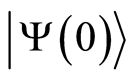 and
and 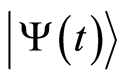 are defined by Equations (26) and (30). With the help of Equations (32), (34), the expectation values for the atomic operators
are defined by Equations (26) and (30). With the help of Equations (32), (34), the expectation values for the atomic operators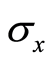 ,
, 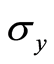 and
and 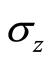
 (35)
(35)
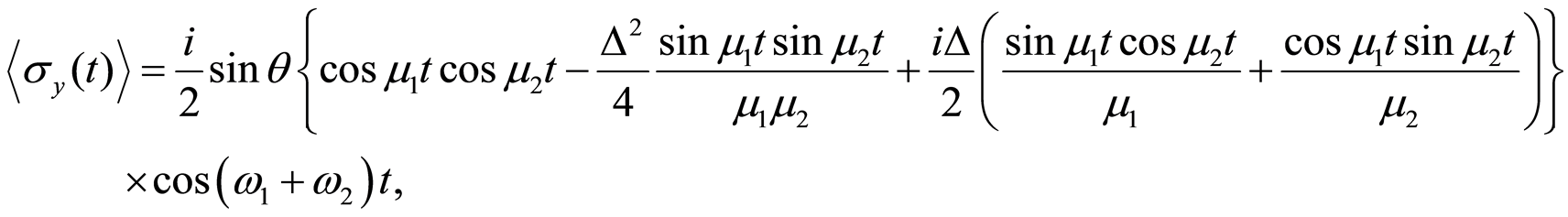 (36)
(36)
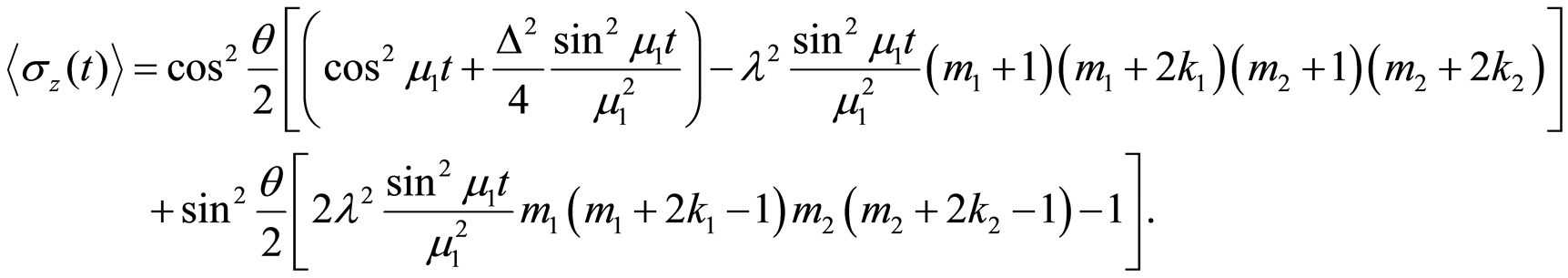 (37)
(37)
Where we have used the abbreviations
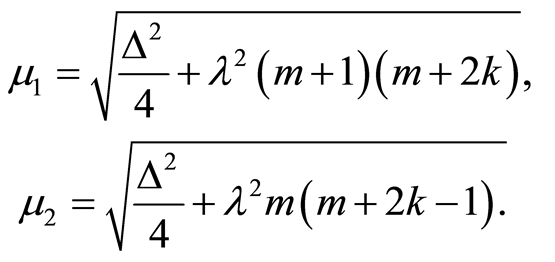 (38)
(38)
3. Scaled Atomic Wehrl Entropy and Marginal Atomic Q-Function
In this section, we will use the scaled atomic Wehrl entropy as an entanglement quantifier between single two level atom and SU(1,1) quantum system.
The scaled atomic Wehrl entropy can be written in terms of the atomic Q function as [25] [26] :
(39)
In the above equation 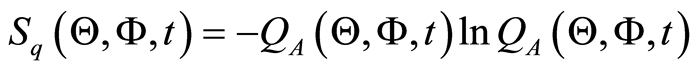 is the atomic Wehrl density and
is the atomic Wehrl density and 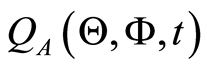 is the atomic
is the atomic 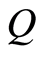 -function which is defined as [27] [28]
-function which is defined as [27] [28]
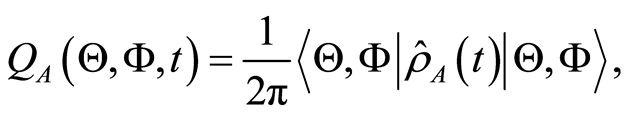 (40)
(40)
where 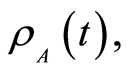 is the reduced density of the atom and
is the reduced density of the atom and 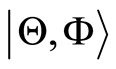 is the atomic coherent state which is defined in the following form
is the atomic coherent state which is defined in the following form
 (41)
(41)
where  and
and 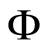 is the atomic phase space parameters. Then the atomic
is the atomic phase space parameters. Then the atomic 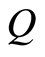 -function can be written in terms of the expectation values of the atomic variables
-function can be written in terms of the expectation values of the atomic variables ,
, 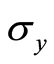 and
and 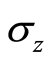 as follows
as follows
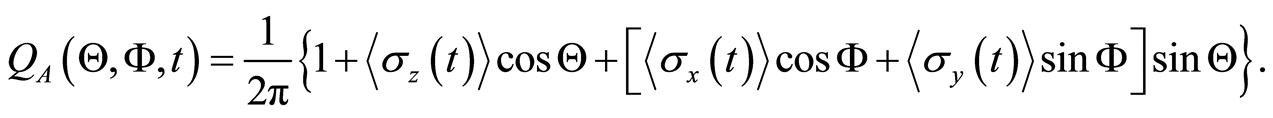 (42)
(42)
It is worth noting that from the definition (39) the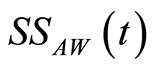 , cannot be negative as a result of the
, cannot be negative as a result of the 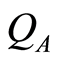 is a non-negative function. As it is generally difficult to find a closed form for the
is a non-negative function. As it is generally difficult to find a closed form for the 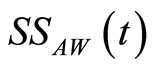 numerical techniques have to be used. Nevertheless, at particular values of the interaction parameters the exact form can be obtained. The shifted (scaled)
numerical techniques have to be used. Nevertheless, at particular values of the interaction parameters the exact form can be obtained. The shifted (scaled) 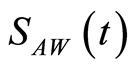 satisfies the following inequality
satisfies the following inequality
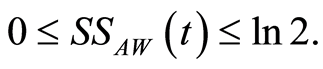 (43)
(43)
By integrating the atomic Wehrl density 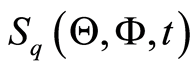 over the atomic variable
over the atomic variable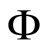 , we obtain the marginal atomic Wehrl density as follows
, we obtain the marginal atomic Wehrl density as follows
 (44)
(44)
4. Some Statistical Aspects
In this section, we discuss and present some statistical aspects such as the atomic inversion , scaled atomic Wehrl entropy
, scaled atomic Wehrl entropy  and marginal atomic Wehrl density
and marginal atomic Wehrl density . We have considered the time has been scaled “one the unit of time is given be the inverse of the coupling constant
. We have considered the time has been scaled “one the unit of time is given be the inverse of the coupling constant ”.
”.
The atomic inversion of the atom is one of the important atomic dynamic variables of the system. This in fact would give us information about the behavior of the atom state during interaction time. In Figure 1, we have plotted the dynamical behavior for different values of the involved parameters. We concentrate on the variation of the initial atomic position 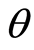 from the excited state, i.e.
from the excited state, i.e. 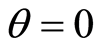 to the superposition state, i.e.
to the superposition state, i.e. 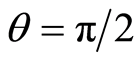 as well as on the excitation number
as well as on the excitation number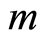 , which is in analogy with the usual Jaynes-Cummings model, corresponding to the number of photons. Firstly, we consider that the system is initially in the excited state
, which is in analogy with the usual Jaynes-Cummings model, corresponding to the number of photons. Firstly, we consider that the system is initially in the excited state  and the absence of the detuning parameter
and the absence of the detuning parameter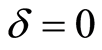 . It is observed that the atomic population inversion has a regular and periodic oscillation where the amplitude of oscillation is decreased when
. It is observed that the atomic population inversion has a regular and periodic oscillation where the amplitude of oscillation is decreased when 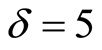 (see Figure 1(c)). Figures 1(b), (d) depict the effect of the superposition state (i.e.
(see Figure 1(c)). Figures 1(b), (d) depict the effect of the superposition state (i.e.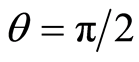 ), where the amplitude of oscillations is very small when the detuning parameter is taken into consideration (see Figure 1(d)).
), where the amplitude of oscillations is very small when the detuning parameter is taken into consideration (see Figure 1(d)).
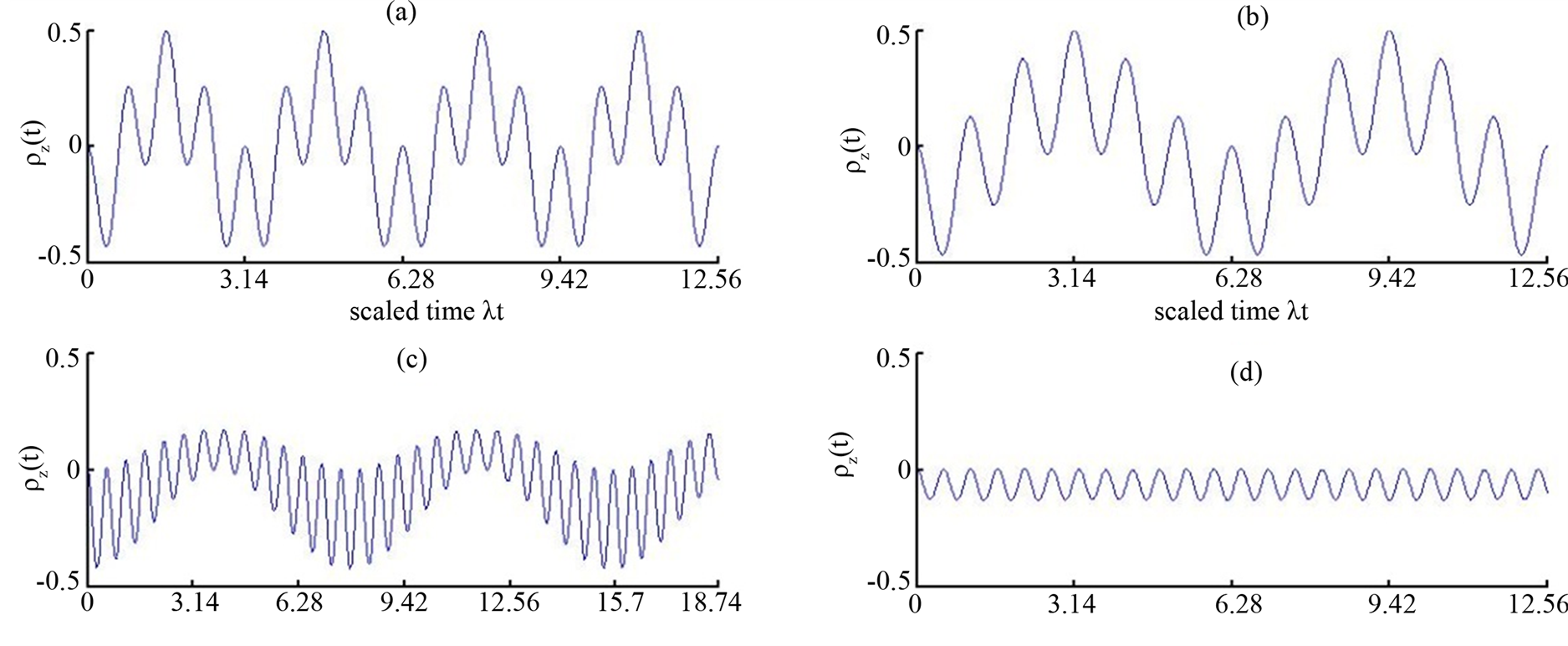
Figure 1. Time evolution of the atomic inversion  for
for 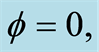
 and the excitation number
and the excitation number 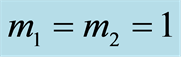 and with different values of the initial atomic position
and with different values of the initial atomic position  and detuning parameter
and detuning parameter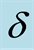 , where (a)
, where (a) , (b)
, (b)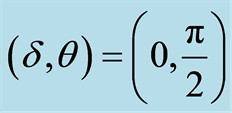 , (c)
, (c) 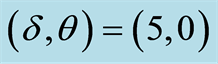 and (d)
and (d) .
.
Figure 2 depicts the dynamical behavior of the scaled atomic Wehrl entropy 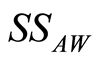 for different values of detuning parameter and initial atomic position when the phase shift between the two levels is neglected and the excitation number is taken to be the unity. From Figure 1(a), one can infer that before the interaction the scaled atomic Wehrl entropy is equal to zero and information about energy levels is not available. This implies that entanglement cannot be performed before the interaction is switched on. As the scaled time goes on, one see that
for different values of detuning parameter and initial atomic position when the phase shift between the two levels is neglected and the excitation number is taken to be the unity. From Figure 1(a), one can infer that before the interaction the scaled atomic Wehrl entropy is equal to zero and information about energy levels is not available. This implies that entanglement cannot be performed before the interaction is switched on. As the scaled time goes on, one see that 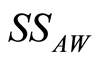 is growing and reaches a local maximum value but after a sometime interaction the difference between local maximum and local minimum becomes bigger. The system returns on its separable state (i.e.
is growing and reaches a local maximum value but after a sometime interaction the difference between local maximum and local minimum becomes bigger. The system returns on its separable state (i.e.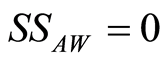 ) at
) at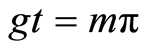 , where
, where . The high amount of entanglement is achieved around the half of periodic time at
. The high amount of entanglement is achieved around the half of periodic time at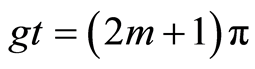 . The amplitude of
. The amplitude of  is decrees which means that the case of weak entanglement between the two-level atom and input field when the effect of the detuning parameter is taken into account (see Figure 2(c)). It is observed that the dynamical behavior of
is decrees which means that the case of weak entanglement between the two-level atom and input field when the effect of the detuning parameter is taken into account (see Figure 2(c)). It is observed that the dynamical behavior of  is completely changed when the two-level atom starts the interaction from the superposition state
is completely changed when the two-level atom starts the interaction from the superposition state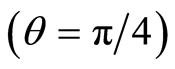 . In general one can see that the high amount of entanglement is achieved during the time evolution in the comparison with the upper state case
. In general one can see that the high amount of entanglement is achieved during the time evolution in the comparison with the upper state case . On the other hand
. On the other hand 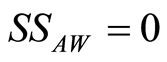 is dropped to zero at
is dropped to zero at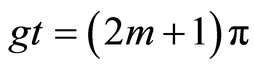 . Finally, Figure 2(d) presents the influence of the detuning parameter on the evolution of
. Finally, Figure 2(d) presents the influence of the detuning parameter on the evolution of 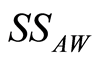 when the initial atomic position
when the initial atomic position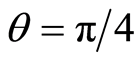 .
.
Now we are in a position to discuss the evolution of the marginal atomic Wehrl density 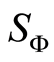 as a function of the time and atomic phase space parameter
as a function of the time and atomic phase space parameter 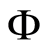 for different values of initial state setting and detuning parameter. It is interesting to mention here that the behavior of
for different values of initial state setting and detuning parameter. It is interesting to mention here that the behavior of 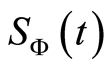 for different values of the non-fluctuating components of Rabi frequency. It is observed that
for different values of the non-fluctuating components of Rabi frequency. It is observed that 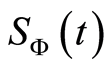 oscillates between minimum and maximum peaks during the time evolution. The distribution of the marginal atomic Wehrl density peaks in depending the initial state setting of the two-level atom when the effect detuning parameter is neglected. The behavior of
oscillates between minimum and maximum peaks during the time evolution. The distribution of the marginal atomic Wehrl density peaks in depending the initial state setting of the two-level atom when the effect detuning parameter is neglected. The behavior of 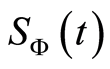 peaks becomes regular and periodic when the effect of the detuning parameter is considered. In this case there the initial state setting has weak effect on the dynamical behavior of
peaks becomes regular and periodic when the effect of the detuning parameter is considered. In this case there the initial state setting has weak effect on the dynamical behavior of  (Figure 3).
(Figure 3).
5. Conclusion
Quantum entanglement is a key resource which distinguishes quantum information theory from classical one. It plays a central role in quantum information and computation. In this paper, we have discussed the problem of the interaction between two-level atom and SU(1,1) quantum system. The model was considered when the twolevel atom is initially in superposition state and the expectation values of the atomic variable are obtained
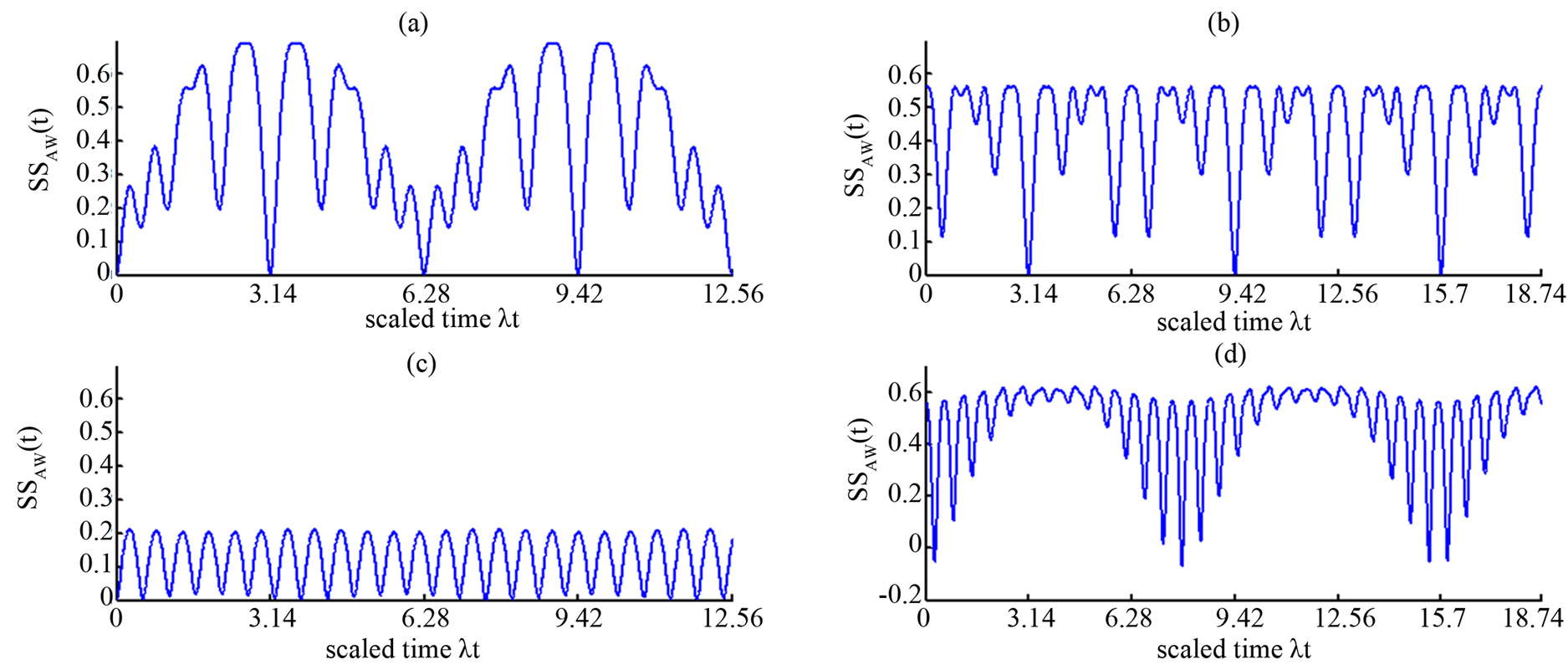
Figure 2. Time evolution of the scaled atomic Wehrl entropy , for
, for 
 and the excitation number
and the excitation number 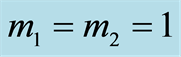 and with different values of the initial atomic position
and with different values of the initial atomic position  and detuning parameter
and detuning parameter , where (a)
, where (a)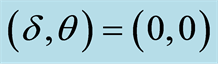 , (b)
, (b)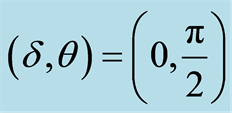 , (c)
, (c) 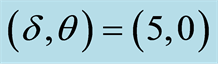 and (d)
and (d)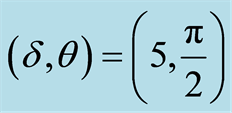 .
.
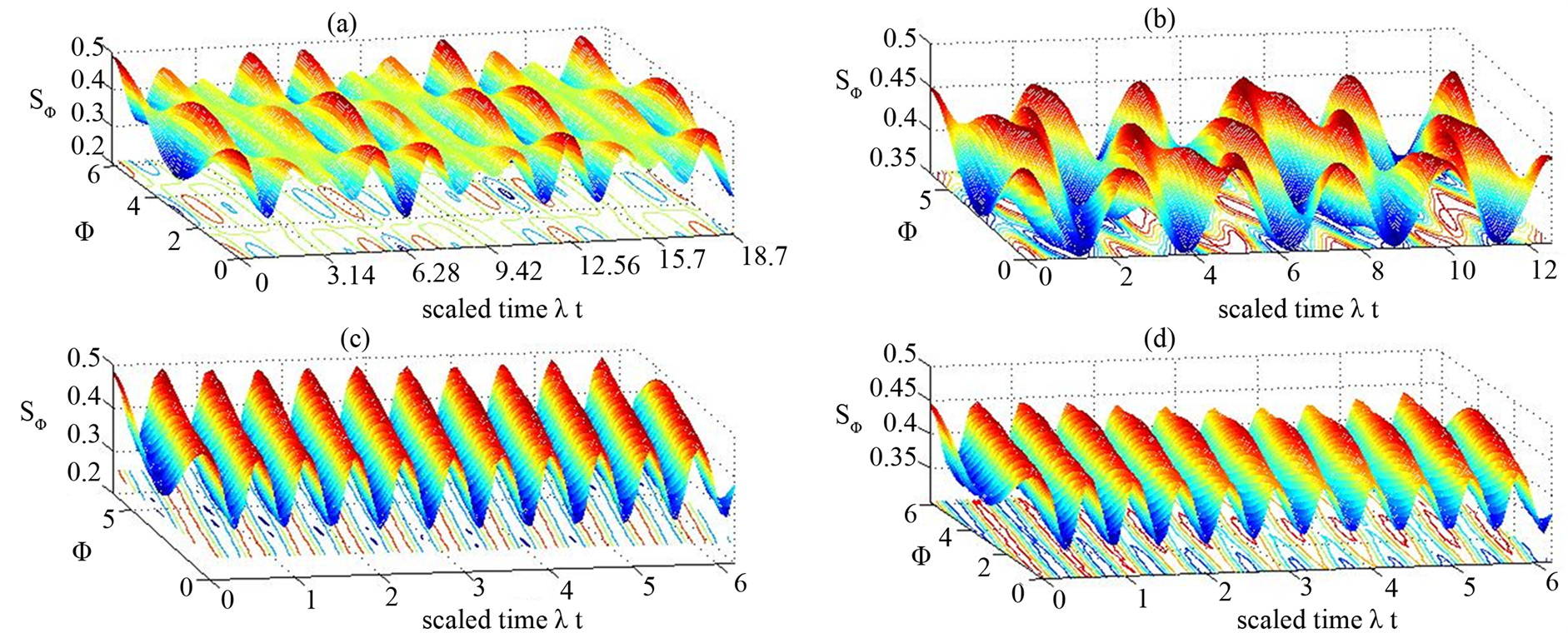
Figure 3. The surface plot of the marginal atomic Wehrl entropy 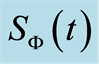 versus the scaled time
versus the scaled time 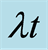 and the phase space parameter
and the phase space parameter  for
for 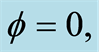
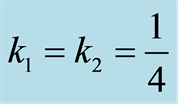 and the excitation number
and the excitation number 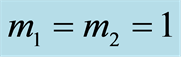 and with different values of the initial atomic position
and with different values of the initial atomic position  and detuning parameter
and detuning parameter , where (a)
, where (a)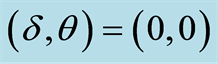 , (b)
, (b) , (c)
, (c) 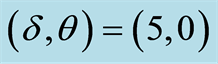 and (d)
and (d)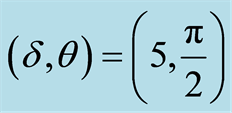 .
.
analytically. Using the scaled atomic Wehrl entropy the system entanglement has been investigated. The analysis herein has been carried out at two distinct considerations of the detuning parameter and initial atomic state setting. Our results show that the SU(1,1) quantum field-atom interaction considering the effect of the initial state setting and detuning parameter has much richer structure. The initial atomic state position and detuning parameter has an important role on the dynamics of the atomic inversion, scaled atomic Wehrl entropy and marginal atomic Wehrl density.
References
- von Neumann, J. (1955) Mathematical Foundations of Quantum Mechanics. rinceton University Press, Princeton.
- Berrada, K., Fanchini, F. and Abdel-Khalek, S. (2012) Quantum Correlations between Each Qubit in a Two-Atom System and the Environment in Terms of Interatomic Distance. Physical Review A, 85, Article ID: 052315. http://dx.doi.org/10.1103/PhysRevA.85.052315
- Berrada, K., Abdel-Khalek, S. and Obada, A.-S.F. (2012) Quantum Fisher Information for a Qubit System Placed inside a Dissipative Cavity. Physics Letters A, 376, 1412-1416. http://dx.doi.org/10.1016/j.physleta.2012.03.023
- Wisemann, H.M. and Milburn, G.J. (2010) Quantum Measurement and Control. Cambridge University Press, Cambridge.
- Popescu, S. and Rohrlich, D. (1997) Thermodynamics and the Measure of Entanglement. Physical Review A, 56, Article ID: R3319. http://dx.doi.org/10.1103/PhysRevA.56.R3319
- Lopez, C.E., Romero, G., Lastra, F., Solano, E. and Retamal, J.C. (2008) Sudden Birth versus Sudden Death of Entanglement in Multipartite Systems. Physical Review Letters, 101, Article ID: 080503. http://dx.doi.org/10.1103/PhysRevLett.101.080503
- Abdel-Aty, M., Abdalla, M.S. and Obada, A.S.F. (2001) Quantum Information and Entropy Squeezing of a Two-Level Atom with a Non-Linear Medium. Journal of Physics A: Mathematical and General, 34, 9129. http://dx.doi.org/10.1088/0305-4470/34/43/303
- Zhang, J.-S. and Chen, A.-X. (2012) Review of Quantum Discord in Bipartite and Multipartite Systems. Quantum Physics Letters, 1, 69-77.
- Mohamed, A.-B.A. (2013) Quantum Discord and Its Geometric Measure with Death Entanglement in Correlated Dephasing Two Qubits System. Quantum Physics, 1, 1-7.
- Abdel-Aty, M. (2005) Information Entropy of a Time-Dependent Three-Level Trapped Ion Interacting with a Laser Field. Journal of Physics A: Mathematical and General, 38, 8589. http://dx.doi.org/10.1088/0305-4470/38/40/008
- Abdel-Aty, M. (2007) Quantum Information Entropy and Multi-Qubit Entanglement. Progress in Quantum Electronics, 31, 1-49.
- Manue Moya-Cessa, H. and Christodoulides, D.N. (2013) A Simple Way to Reconstruct the Wigner Function. Applied Mathematics & Information Sciences, 7, 839-841. http://dx.doi.org/10.12785/amis/070301
- Gravel, C. (2012) Structure of the Probability Distribution for the GHZ Quantum State under Local von Neumann Measurements. Quantum Physics Letters, 1, 87.
- Ahmed, A.-H.M., Zakaria, M.N. and Metwally, N. (2012) Teleportation in the Presence of Technical Defects in Transmission Stations. Applied Mathematics & Information Sciences, 6, 781.
- Miranowicz, A., Matsueda, H. and Wahiddin, M.R.B. (2000) Classical Information Entropy and Phase Distributions of Optical Fields. Journal of Physics A: Mathematical and General, 33, 5159. http://dx.doi.org/10.1088/0305-4470/33/29/301
- Leonski, W., Miranowicz, A. and Piatek, K. (2003) Classical Information Entropy for Single and Two Mode Quantum Fields. In Nowak, J., Zajac, M. and Masajada, Jan., Eds., Proceedings of the SPIE, 13th Polish-Czech-Slovak Conference on Wave and Quantum Aspects of Contemporary Optics, 21 November 2003, 5259, 37-41. http://dx.doi.org/10.1117/12.545063
- Jex, I. and Orlowski, A. (1994) Wehrl’s Entropy Dynamics in a Kerr-Like Medium. Journal of Modern Optics, 41, 2301. http://dx.doi.org/10.1080/09500349414552151
- El-Barakaty, A., Darwish, M. and Obada, A.-S.F. (2011) Purity Loss for a Cooper Pair Box Interacting Dispersively with a Nonclassical Field under Phase Damping. Applied Mathematics & Information Sciences, 5, 122.
- Abdel-Khalek, S. (2009) Wehrl Entropy and Wehrl Phase Distribution of a Single-Trapped Ion Interacting with a Laser Field. Physica Scripta, 80, Article ID: 045302. http://dx.doi.org/10.1088/0031-8949/80/04/045302
- Abdel-Khalek, S., Khalil, E.M. and Ali, S.I. (2008) Entanglement of a Two-Level Atom Papered in a Finite Trio-Coherent State. Laser Physics, 18, 135-143. http://dx.doi.org/10.1134/S1054660X08020072
- Abdel-Khalek, S. and Obada, A.-S.F. (2010) New Features of Wehrl Entropy and Wehrl PD of a Single Cooper-Pair Box Placed inside a Dissipative Cavity. Annals of Physics, 325, 2542-2549. http://dx.doi.org/10.1016/j.aop.2010.05.011
- Eiselt, J. and Risken, H. (1991) Quasiprobability Distributions for the Jaynes-Cummings Model with Cavity Damping. Physical Review A, 43, 346-360, http://dx.doi.org/10.1103/PhysRevA.43.346
- Walls, D.F. and Millburn, G.J. (1985) Effect of Dissipation on Quantum Coherence. Physical Review A, 31, 2403-2408. http://dx.doi.org/10.1103/PhysRevA.31.2403
- Abdel-Khalek, S., Zidan, N. and Abdel-Aty, M. (2011) Analysis of Mixed State Entanglement with Intrinsic Decoherence. Physica E, 44, 6. http://dx.doi.org/10.1016/j.physe.2011.06.007
- Abdel-Khalek, S. (2007) Atomic Wherl Entropy in a Two-Level Atom Interacting with a Cavity Field. Applied Mathematics & Information Sciences, 1, 53-64.
- Abdel-Khalek, S., Abdel-Hameed, H.F. and Abdel-Aty, M. (2011) Atomic Wehrl Entropy of a Single Qubit System. International Journal of Quantum Information, 9, 967-979. http://dx.doi.org/10.1142/S0219749911007538
- Dermez, R. and Abdel-Khalek, S. (2011) Atomic Wehrl Entropy and Negativity as Entanglement Measures for Qudit Pure States in a Trapped Ion. Journal of Russian Laser Research, 32, 287-297. http://dx.doi.org/10.1007/s10946-011-9215-1
- Abdel-Khalek, S., Khalil, E.M. and Ali, S.I. (2008) Entanglement of a Two-Level Atom Papered in a Finite Trio-Coherent State. Laser Physics, 18, 135-143. http://dx.doi.org/10.1134/S1054660X08020072

