Journal of Quantum Information Science
Vol. 3 No. 4 (2013) , Article ID: 40161 , 11 pages DOI:10.4236/jqis.2013.34019
Revealing the Ubiquitous Effects of Quantum Entanglement—Toward a Notion of God Logic
1Department of Computer Science, Georgia Southern University, Statesboro, USA
2Jiann-Ping Hsu College of Public Health, Georgia Southern University, Statesboro, USA
Email: wrzhang@georgiasouthern.edu, kepeace@georgiasouthern.edu
Copyright © 2013 Wen-Ran Zhang, Karl E. Peace. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received September 16, 2013; revised October 26, 2013; accepted November 9, 2013
Keywords: Ubiquitous Effects of Quantum Entanglement; Programming the Universe; Negative-Positive Energy Supersymmetry; Scientific Unification; Ubiquitous Quantum Computing; Quantum Intelligence
ABSTRACT
Following Spinoza-Einstein’s interpretation of God or nature, the notion “God Logic” is proposed. This notion is to serve as an elicitation for a consistent set of necessary criteria for: 1) developing the logical foundation of quantum gravity as envisaged by Einstein, 2) revealing the ubiquitous effects of quantum entanglement as suggested by Roger Penrose, and 3) programming the universe as proposed by Seth Lloyd. An evolving set of eleven criteria is proposed for the notion. The possibility of inventing such a logical system is analyzed. A supersymmetrical candidate logic of negative-positive energy dynamic equilibrium is introduced and assessed against the set of criteria. It is shown that the first 10 criteria are met or partially met by the candidate. But the question whether the 11th criterion has been or can be met is left open for discussion and further research effort. The assessment leads to a few predictions. Notably, it is predicted that, should Boson-Fermion symmetry or broken symmetry be observed, it would be caused by bipolar symmetry or broken symmetry of negative-positive energies.
1. Introduction
British mathematical physicist Roger Penrose identified two mysteries of quantum entanglement [1, p. 591]. The first is characterized as the phenomenon itself. The second, according to Penrose, is “How are we to come to terms with quantum entanglement and to make sense of it in terms of ideas that we can comprehend, so that we can manage to accept it as something that forms an important part of the workings of our actual universe?.. The second mystery is somewhat complementary to the first. Since according to quantum mechanics, entanglement is such a ubiquitous phenomenon—and we recall that the stupendous majority of quantum states are actually entangled ones—why is it something that we barely notice in our direct experience of the world? Why do these ubiquitous effects of entanglement not confront us at every turn? I do not believe that this second mystery has received nearly the attention that it deserves, people’s puzzlement having been almost entirely concentrated on the first.”
A closely related topic to the two quantum mysteries is Programming the Universe as proposed by MIT professor Seth Lloyd, which is one of his book titles. The book posits the universe itself as a giant quantum computer [2]. According to Lloyd, the universe is all about quantum information processing. Once we understand the laws of physics completely, we will be able to use small-scale quantum computing to understand the universe completely as well.
Is Lloyd serious? The answer is “of course” because Einstein also asserted that “Pure thought can grasp reality, as the ancients dreamed” and “nature is the realization of the simplest conceivable mathematical ideas.” Einstein famously stated: “I believe in Spinoza’s God who reveals himself in the orderly harmony of what exists, not in a God who concerns himself with the fates and actions of human beings.” Einstein also said: “Everyone who is seriously involved in the pursuit of science becomes convinced a spirit is manifest in the laws of the Universe—a spirit vastly superior to that of man, and one in the face of which we with our modest powers must feel humble. In this way, the pursuit of science leads to a religious feeling of a special sort, which is indeed quite different from the religiosity of someone more naive.”
Spinoza-Einstein’s God, Penrose’s quantum mysteries, and Lloyd’s startling thesis opened the door to the notion of God logic. Regardless of the proper or improper usage of the “God Particle” nickname, the name “God Logic” seems to be the best option for revealing the ubiquitous effects of quantum entanglement and programming all the particles of the universe. As an individual particle the God Particle is perhaps better called the Higgs Boson, but any alternative name other than “God Logic” might be inappropriate or inadequate for its holistic nature of revealing and programming. For instance, if we call it “Logic of Nature”, it may lose its holistic implications of social, biological and mental aspects as well as natureman harmony; if we call it “Logic of Science”, it may miss out its implications in philosophy; if we call it “Logic of Philosophy”, it will exclude its scientific bearings; if we call it “Universal Logic”, it may offend the universal logic community because of its stance against contradiction which is central in universal logic research. After all, a name is just a name. Until a better name comes up, we have to make a best selection.
The notion “God Logic” is proposed in this work. The scope of the notion is bounded in nature, science and philosophy, irrelevant to anyone’s personal religious belief. It is to serve as an elicitation for a consistent set of necessary criteria of: 1) developing the logical foundation for quantum gravity; 2) revealing the ubiquitous effects of quantum entanglement; 3) programming the universe.
This work is organized into six sections. Section 2 proposes an evolving set of 11 criteria for the notion of God logic. Section 3 analyzes the possibility of inventing such a logical system. Section 4 introduces a candidate. Section 5 presents an assessment on the candidate against the set of criteria with a few predictions. Section 6 draws a few conclusions.
2. Criteria
The unusual God logic should meet an unusual set of criteria. Here is an evolving set of 11 such criteria:
(1) Causality Criterion: Aristotle’s causality principle has been deemed the doctrine of all sciences. Many believe that causality is holding the key for quantum gravity—the grand unification of relativity and quantum mechanics. Unfortunately, the principle was stated only in words 2300 years ago. All established truth-based logical systems have so far failed to provide logically definable causality with regularity [3]. The God logic, therefore, must provide certain formal, logically definable, and fundamental causality for nature and science.
(2) Computability Criterion: In order to program the universe, the God logic has to be both logical and computational. It has to subsume and be recoverable to classical truth-based logic. It must be contradiction-free. Therefore, it has to be a generalization of Boolean logic [4] without compromising the basic law of excluded middle.
(3) Relativity Criterion: In order to provide a logical foundation for the unification of general relativity and quantum mechanics the God logic must provide certain logically definable quantum relativity.
(4) Quantum Entanglement Criterion: The God logic must support quantum computing for programming the universe. Therefore, it must provide certain fundamental logically definable quantum entanglement.
(5) Simplicity Criterion: As asserted by Einstein and Lloyd, the God logic must be simple and meaningful.
(6) Hilbert Problem 6 Criterion: In order to program the universe and all beings in the universe, the God logic has to be the logic of physics. Therefore, it must provide a minimal but most general solution to Hilbert Problem 6—“Axiomatizing all of physics.”
(7) Geometric and Set-Theoretic Criterion: The combination of general relativity and quantum theory introduces a minimum measurable distance—the Planck length, and such a distance implies that neither space nor particles can form classical sets. Without sets, axioms cannot be defined and an axiomatic description of foundational physics becomes impossible. In order to regulate spacetime, the God logic must be based on a new set theory as the ontological basis for an axiomatic description of foundational physics and the new set theory must be hosted within a new geometry that transcends spacetime.
(8) Ubiquity Criterion: In order to reveal the ubiquitous effects of quantum entanglement in the real world, the God logic must characterize fundamental social, mental, and biological properties as well as logical and physical ones with quantum entanglement.
(9) Unification Criterion: In order to program the universe, the God logic must lead to logical or qualitative (not necessarily quantitative) unifications of matter-antimatter, particle-wave, big bang and black hole, relativity and quantum mechanics.
(10) Philosophy Criterion: As God logic, it must unify truth and equilibrium, physics and metaphysics as well as science and philosophy. Thus, it must answer the end and death assertions on philosophy [5,6] with a scientific reincarnation of philosophy.
(11) Consistency Criterion: Gödel’s first incompleteness theorem shows that systems having at least the properties of Peano arithmetic cannot be both complete and consistent. Gödel’s 2nd incompleteness theorem shows that no system with such properties can be proven consistent within itself, unless it is an inconsistent system. The God logic must have the properties of Peano arithmetic and has to overturn Gödel’s two theorems and prove its own consistency within itself because as God logic it cannot expect other logic to prove its consistency.
3. Possibility
Is the God logic possible at all? It is well-known that Einstein was a friend and colleague of Gödel at Princeton University. Before fleeing from Nazi Germany to resettle in the United States, Einstein once visited German mathematician Hilbert by invitation and was aware of Hilbert’s programs in mathematics and axiomatizing physics [7]. Einstein asserted in 1916 [8]: “Physics constitutes a logical system of thought which is in a state of evolution, whose basis (principles) cannot be distilled, as it were, from experience by an inductive method, but can only be arrived at by free invention.” Evidently, Einstein believed that it is possible to axiomatize physics.
In 1931, Gödel published his incompleteness theorems [9]. Many believe that these theorems proved Hilbert’s mathematical program impossible and also shattered his hope for axiomatizing physics as a related program. Three years after Gödel published his incompleteness theorems, however, Einstein reaffirmed [10] that “pure thought can grasp reality” and “nature is the realization of the simplest conceivable mathematical ideas.” In 1940, nine years after Gödel published his incompleteness theorems, Einstein asserted [11] that the grand unification of general relativity and quantum mechanics needs a new logical foundation: “For the time being we have to admit that we do not possess any general theoretical basis for physics which can be regarded as its logical foundation.”
Evidently, Einstein never wavered on a logical foundation for physics. Hilbert lived for 12 years after Gödel published his incompleteness theorems. Many wondered why Hilbert did not concede or officially respond to Gödel’s findings. A sober view is that, if Einstein refused to give up hope for the God logic, why should Hilbert?
Gödel’s incompleteness theorems, Hilbert’s effort in axiomatizing physics, and Einstein’s assertion on a new logical foundation for physics were all giant steps. It should be remarked, however, the three giants stopped short of pointing out the inevitable [12, p. 92]:
1. The incompleteness of truth-based reasoning is due to its lack of syntax and semantics for the fundamental physical concept “equilibrium” or “symmetry”.
2. A logical foundation for physics requires a philosophically deeper cosmology beyond spacetime and a different mathematical abstraction beyond classical being-centered and truth-based unipolar cognition.
From the eleven criteria, it seems that a geometry that transcends being, truth and spacetime is the key for hosting the God logic. But what geometry could possibly go beyond spacetime? The answer is the geometry of equilibrium or supersymmetry of negative-positive energies or the Yin and the Yang of nature. Since no system can violate the equilibrium or non-equilibrium condition of the 2nd law of thermodynamic, an equilibrium-based dynamic logic that reasons on equilibrium, quasi-equilibrium and non-equilibrium (or symmetry and broken symmetry) will transcend spacetime as well as all beings and truths within it. In brief, nothing can escape equilibrium, quasi-equilibrium or non-equilibrium as we say that the universe is either an equilibrium or non-equilibrium but not vice versa.
It should be noted that the supersymmetry of negativepositive energies suggested in this paper is different from that of boson-fermion particles. While boson-fermion supersymmetry is an unobserved theory, it is observable facts that every action is matched with its reaction; dipoles are everywhere; every boson or fermion particle may have an antiparticle; parity non-conservation and CP-violation are observable; the universe is regulated by negative-positive energies. Thus, the Yin and the Yang of nature are non-isomorphic observable bipolar coexistence.
For instance, the subatomic particle B-sub-s meson discovered at the Fermi National Accelerator Laboratory [13] can switch between matter and antimatter particle three trillion times per second before decaying. It can be deemed evidence for negative-positive energy supersymmetry and a shakeup of boson-fermion supersymmetry.
It might be argued that, in the Standard Model, the Higgs particle is a boson with no spin, electric charge, or color charge. This can be countered by the fact that Higgs particle is a quantum excitation of one of the four components of the Higgs field with two neutral and two charged components constituting a scalar field. Evidently each pair possesses either action-reaction or negativepositive bipolarity. Thus, bipolarity can be deemed the key for bipolar equilibrium or non-equilibrium and bipolar symmetry or broken symmetry can be posited the cause of boson-fermion symmetry or broken symmetry should the latter be observed. While the confirmation and unification of the two different possible symmetries are left open for further research effort, the observable supersymmetry of negative-positive energies can be posited more fundamental and general which governs the microscopic particle world as well as the macroscopic physical, logical, biological, mental, and social worlds.
4. A Candidate
YinYang bipolar dynamic logic (BDL) [12,14,15] may serve as an equilibrium-based (vs. truth-based) candidate for the God logic role. BDL is based on bipolar sets whose elements are bipolar agents such as dipoles, particle-antiparticle pairs, nature’s action-reaction, genomic repression-activation capacities of regulator protein YinYang1 [16], social competition-cooperation relations [17], input-output energies of any system, self-negation and self-assertion abilities in mental health [18,19], in general, the negative and positive energies [6] or the Yin and Yang of nature (Figure 1).
Is YinYang bipolarity more fundamental than truth and spacetime? First, bipolar equilibrium or non-equilib- rium is a generic type of equilibrium or non-equilibrium. It is well-known that the century long intensive search for monopoles has so far failed. Without monopole, string theory is not testable. But dipoles are everywhere. It is also a common belief that particle-antiparticle pairs are the only stuff that survived the big bang and they also are the only stuff that will survive a black hole due to particle-antiparticle emission or Hawking radiation [20, 21]. Thus, YinYang bipolarity as the generic property or essence of equilibrium, quasi-equilibrium and non-equilibrium can be posited the most fundamental property of the universe according to the 2nd law of thermodynamics, and it has to be more fundamental than truth and spacetime. Thus, BDL can be more physical and less philosophical than truth-based logic which was originated in ancient Greece with the assumption of a flat stationary Earth as the center of the universe.
BDL is defined on B1 = {−1,0} ´ {0,+1} = {(0,0), (0,+1), (−1,0), (−1,+1)} – a bipolar quantum lattice in YinYang bipolar geometry as shown in Figure 2. The four values of B1 form a bipolar causal set [12] which stand respectively for eternal equilibrium (0,0), nonequilibrium (−1,0), another non-equilibrium (0,+1); equilibrium or harmony (−1,+1). Equations (1)-(12) in Table 1 provide the basic operations of BDL. The laws in Table 2 hold on BDL.
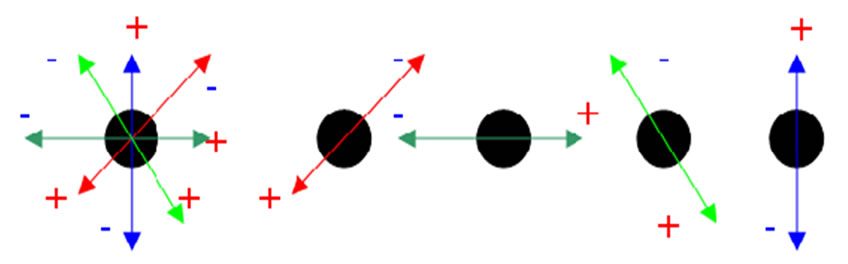
Figure 1. Multidimensional equilibrium or non-equilibrium deconstructed to bipolar equilibria/non-equilibria.
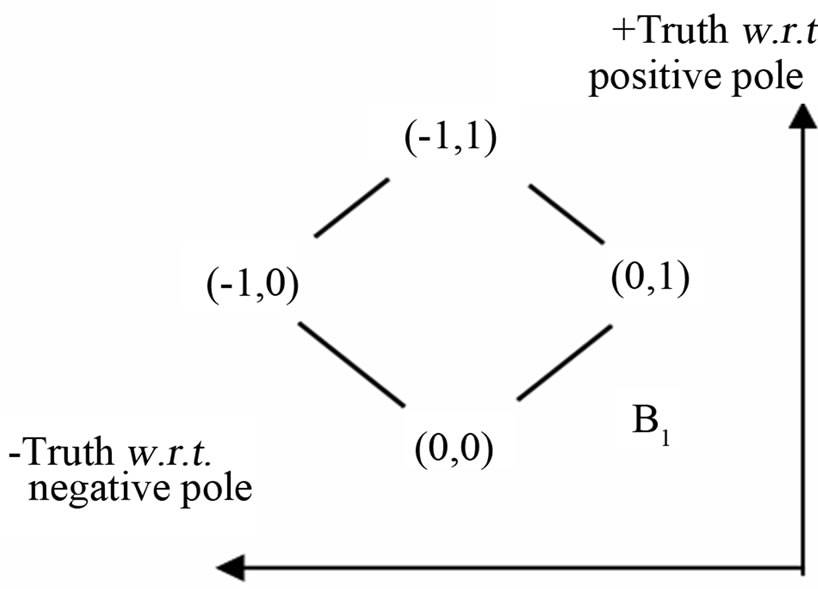
Figure 2. Hasse diagram of B1 in YinYang bipolar geometry.

Table 1. YinYang Bipolar Dynamic Logic (BDL).

Table 2. Some bipolar laws
An axiomatization of BDL is presented in Table 3 for consistency assessment. In BDL Å and Å− are “balancers”; Æ and Ä are intuitive “oscillators”; Æ− and Ä− are counter-intuitive “oscillators”; & and &− are “minimizers” or “annihilators.” A key element in the axiomatization is bipolar universal modus ponens (BUMP) (Table 4). The linear, cross-pole, bipolar fusion, fission, oscillation, interaction and entanglement properties are depicted in Figure 3.
Based on bipolar sets and BDL, a bipolar relation R in a bipolar set X is defined as an equilibrium relation if it is bipolar symmetric, reflexive, and transitive. It has been proven that an equilibrium relation can be a non-linear bipolar fusion of many equivalence relations of conflict, coalition, and/or harmony sets [12, Ch. 3-5]. The notions of conflict and coalition characterize pockets of nonequilibrium or disharmony within a global equilibrium and harmony.
Logical and algebraic extensions of BDL are presented

Figure 3. YinYang bipolar relativity: (a) Linear interaction; (b) Cross-pole non-linear interaction; (d) Oscillation; (e) Bipolar entanglement.

Table 3. An equilibrium-based axiomatization

Table 4. Bipolar Universal Modus Ponens (BUMP).
in Ref. [12]. It has been naturally extended from the 4- valued bipolar quantum lattice B1 = {−1,0} ´ {0,+1} to the real-valued bipolar quantum lattices BF = [−1,0] ´ [0,+1] and Bn = {−n,0} ´ {0,+n}, 0 ≤ n ≤ ¥. A bipolar quantum linear algebra (BQLA) has been defined in B¥ = [−n,0] ´ [0,+n], 0 ≤ n ≤ ¥ [12].
5. Assessment
A preliminary assessment on BDL is presented in this section against the eleven criteria. The assessment is for the sole purpose of new idea elicitation. Competing ideas, amendments, and falsifications are especially sought.
Assessment 1 (Causality). Classical modus ponens (MP) can be derived from bipolar universal modus ponens (BUMP) but not vice versa [12, Ch. 3]. This observation qualifies BUMP as a nonlinear bipolar dynamic generalization of MP from truth-based domain to bipolar equilibrium-based domain. BUMP provides formal, fundamental, and logically definable equilibrium-based causality for the first time ever (Tables 3 and 4). Thus, the causality criterion is met.
Philosophically speaking, the being-centered and truth-based approach to science is originated from the belief in ancient Greek time that the Earth was the stationary and flat center of the universe. Without a shred of dynamics, true or false (1 or 0) as static truth values prevent the being-centered and truth-based approach from providing logically definable causality. Now modern science has proven the static assumption untrue. The equilibrium-based approach brings dynamics to logical reasoning with formally definable causality.
Assessment 2 (Computability). Classical 1st order logic or Boolean logic is derivable from BDL but not vice versa [12, Ch. 3,4,5]. This qualifies BDL as a non-linear bipolar dynamic generalization of classical 1st order logic. Despite the non-linearity, BDL satisfies the law of excluded middle and is contradiction-free (Table 2). In addition it has led to the generalizations [12] of equivalence relation to equilibrium relation, fuzzy similarity relation to quasi-equilibrium relation, and linear algebra to bipolar quantum linear algebra. Thus, the computability criterion is met.
The equilibrium-based property distinguishes BDL from all truth-based logical systems. Equilibrium or non-equilibrium is a fundamental condition of the 2nd law of thermodynamics. Truth and falsity, however, do not carry any shred of direct physical semantics. On the other hand, since any physical being must exist in certain equilibrium or non-equilibrium, being and truth can be unified, revealed and regulated under dynamic equilibrium such as input and output. Philosophically speaking, the essence of being is not truth but YinYang bipolar dynamic equilibrium.
It should be remarked that contradiction (being both true and false) is permissible in some logical systems. Noticeably, contradiction is deemed the essence of being in Hegelian and Marxist dialectics. In BDL YinYang bipolar dynamic equilibrium is posited the essence of being, and contradiction is deemed non-essential phenomenon.
Assessment 3 (Relativity). BUMP provides logically definable quantum relativity with bipolar variables of action-reaction objects [12, Ch. 6]. It can be stated that, for all bipolar variables or functions f, j, y, and c, IF (f Þ j) & (y Þ c), THEN the bipolar interaction (f * y) implies that of (j * c) or formally expressed as (f * y) Þ (j * c). Thus, the relativity criterion is met.
Assessment 4 (Entanglement). BUMP provides logically definable bipolar quantum entanglement with YinYang bipolar variables (Table 4) [12, Ch. 7]. It can be stated that, for all bipolar equilibrium functions f, j, y, IF (f Û j), THEN we must have (f * y) Û (j * y). Thus, the quantum entanglement criterion is met.
Assessment 5 (Simplicity). BDL is simple, much simpler than string theory and M-theory. It is meaningful by providing basic and logically valid equations for bipolar relativity as denoted by Þ
Þ 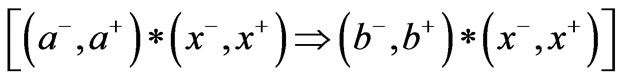 and bipolar quantum entanglement denoted
and bipolar quantum entanglement denoted  Þ
Þ 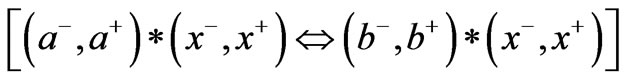 (Note the latter is derivable from the earlier). Thus, the simplicity criterion is met.
(Note the latter is derivable from the earlier). Thus, the simplicity criterion is met.
Here it should be remarked that, unlike string theory, which predicts the existence of monopoles and strings, BDL is based on dipoles, particle-antiparticle pairs, action-reaction and input-output energies which are wellobserved physical realities. Furthermore, the Nobel level discoveries on parity non-conservation and CP-violation have proved the non-isomorphic nature of the negative and positive poles or the Yin and Yang of nature.
Assessment 6 (Hilbert Problem 6). Following the 2nd law of thermodynamics, BDL leads to a supersymmetrical bipolar equilibrium-based axiomatization of physics (Table 3)–a minimal but most general solution to Hilbert Problem 6—“Axiomatizing all of physics”. Thus, the Hilbert Problem 6 criterion is partially met.
After a century, Hilbert’s Problem 6 is now widely deemed unsolvable. With the minimal but most general solution we have the following prediction:
Prediction 1: Although Hilbert Problem 6 is not solvable with truth-based reasoning, it is solvable with equilibrium-based reasoning.
Assessment 7 (Geometric and Set-Theoretic). YinYang bipolar geometry [12] as a completely background-independent geometry does transcend spacetime as evidenced by the fact that quadrant is irrelevant in the new geometry and spacetime can be emerging parameters there (see Equation (13) and Figure 4). Within this new geometry, equilibrium-based bipolar causal sets and BDL can be defined, and the barrier of Planck length is penetrated. Thus, the geometric and set-theoretic criterion is met which qualifies BDL as a new mathematical abstraction.
Defined in YinYang bipolar geometry, BDL unified truth, equilibrium, causality and quantum entanglement. In this unification, bipolar quantum entanglement—a truth-based paradox in spacetime becomes a sound new law in the new geometry. A key element in the unification is BUMP that leads to YinYang bipolar relativity and quantum entanglement of negative-positive energies [12] defined by Equation (13). "a,b,c,d,
 (13)
(13)
In Equation (13), a(tx,p1), b(ty,p2), c(tx,p3), d(ty,p4) are any bipolar agents where a(t, p) stands for “agent a at time t and space p” (tx, ty, px and py can be the same or different points in time and space). An agent without time and space is assumed at any time t and space p. An agent at time t and space p is therefore more specific. The background independent nature of the new geometry makes space and time emergence possible in YinYang bipolar geometry—a very desirable feature in modern physics. (f Û j) also leads to (f Û −j) to subsume
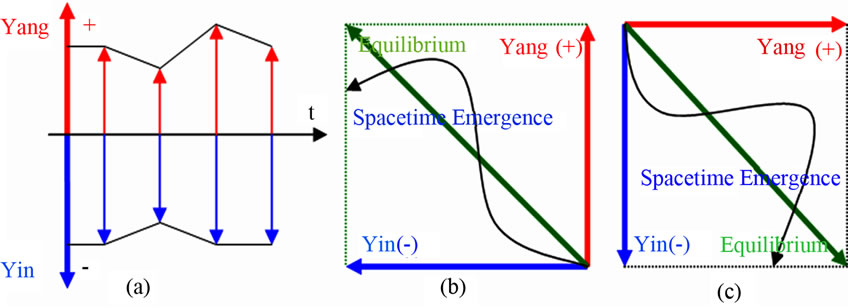
Figure 4. Background-Independent YinYang bipolar geometry: (a) Magnitudes of Yin and Yang; (b) Growing curve; (c) Quadrant Irrelevant Property.
spin anti-correlated entanglement [22].
Assessment 8 (Ubiquity). BDL can reveal the ubiquitous effects of quantum entanglement in social, mental, and biological worlds as well as logical and physical worlds [12,14-19,22-26]. The possible revelations are due to the fact that BDL is based on bipolar sets whose elements are entangled bipolar agents that characterize the fundamental properties of
1. dipoles, particle-antiparticle, action-reaction, negativepositive energies in the physical world;
2. genomic repression-activation of the ubiquitous genomic regulator protein Yin Yang1 [16] and inputoutput energies of any biological system at the molecular, cell or organism levels [12, Ch. 8-9] [24];
3. competition-cooperation in socioeconomics [17,23];
4. self-negation and self-assertion abilities in mental health [18,19].
5. quantum bipolarity for quantum-digital compatibility in computing and communication [12, Ch. 7].
An example in mental health application is illustrated in Figure 5 [18,19] [12, Ch. 10]. Figure 5(a) shows the
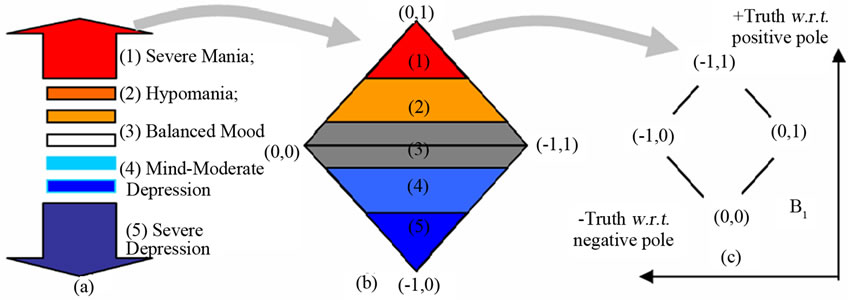
Figure 5. Transformation of DSM-IV standard classification of bipolar disorders to BDL in YinYang bipolar geometry.
standard classification of bipolar disorders in the Diagnostic Statistics Manual (DSM-IV) of NIMH; Figure 5(b) shows a reshape with logical marking; Figure 5(c) shows the transformation to YinYang bipolar geometry.
Dramatically, negative-positive energy dynamic equilibrium provides a supersymmetry for the unification of big bang, black hole, mania, and depression. It is predicted that: (1) Black hole is to a galaxy (or universe) as bipolar depression is to a dysfunctional brain, both can be characterized as (−1,0); big bang is to a galaxy (or universe) as bipolar mania is to a dysfunctional brain both can be characterized as (0,+1); wormhole (if it exists) is to a galaxy (or universe) as bipolar mental equilibrium is to a functional brain and both can be characterized as (−1,+1); if the universe was created by a big bang (0,+1), a big bang could be proceeded by a transient dormant process from black hole (−1,0) to the big bang and followed by an expansion process from the big bang to equilibrium (−1,+1), and then an contraction process from equilibrium to black hole. Eternal equilibrium can be deemed the void or vacuum.
Based on the above, it is clear that the ubiquitous effect criterion is met. Again, the key point is that no natural being in the universe, either physical, biological, social or mental, can escape the equilibrium or non-equilib- rium condition of the 2nd law of thermodynamics. This makes ubiquitous quantum computing possible and leads to the notion of quantum intelligence.
Assessment 9 (Unification). In order to program the universe, the God logic must lead to logical or qualitative (not necessarily quantitative) unifications of matter-antimatter, particle-wave, big bang and black hole, relativity and quantum entanglement. This seems to be a mission impossible. Surprisingly, such unifications are shown achievable through BDL and bipolar quantum linear algebra (BQLA)—an algebraic extension of BDL, and the unification criterion is partially met [12,25].
While BDL is concerned with the logic of reciprocal interactions among individual elements modeled as bipolar equilibrium or non-equilibrium, BQLA is for mathematical characterization of agents modeled as multidimensional equilibriums (see Figures 1 and 6). The mathematical form of BQLA can be the same as classical
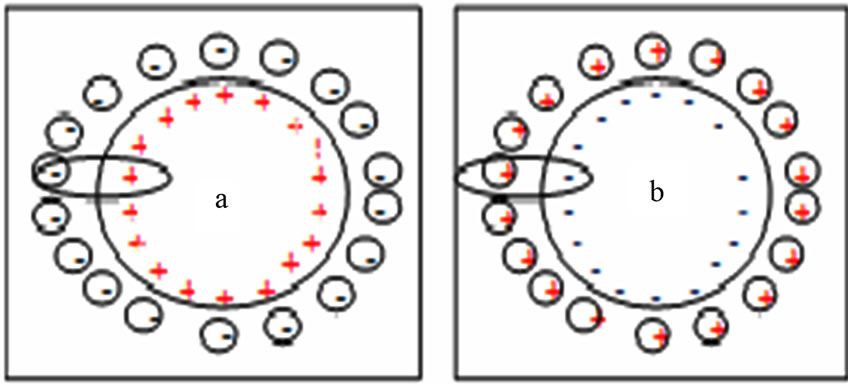
Figure 6. Matter-antimatter unification.
linear algebra except that each element in a bipolar matrix is a bipolar variable reflexing the fact that everything in the universe must be in certain bipolar equilibrium or non-equilibrium. This provides a representational basis for characterizing matter-antimatter atoms, molecular and cellular structures as well as different, social, biological and mental systems [12,24,25].
Figure 6(a) shows a matter atom and Figure 6(b) shows an antimatter atom. It is shown that both can be modeled as multidimensional bipolar equilibriums [25]. Surprisingly, both the matter and antimatter atoms can be unified with a single BQLA equation of negative-positive energy dynamic equilibrium or symmetry (Equation (14)) [25].
In Equation (14), E, M, and V are bipolar matrices whose elements are bipolar variables. This is made possible by the background independent nature of YinYang bipolar geometry (see Figure 4). Furthermore, BQLA shows the potential for achieving quantum gravity because gravitational action-reaction can be taken into consideration as a superposition onto bipolar quantum interaction within a matter or antimatter atom [25].
 . (14)
. (14)
Legendary Danish physicist Niels Bohr, a father figure of quantum mechanics, was the first to bring YinYang into quantum theory for his particle-wave complementarity principle. When he was awarded the Order of the Elephant by the Danish government in 1947, he designed his own coat of arms which featured in the center a YinYang logo (or Taiji symbol) with the Latin motto “contraria sunt complementa” or “opposites are complementary.” (Figure 7)
While Bohr’s quantum mechanics recognized particle-wave complementarity, it stopped short of identifying the essence of YinYang bipolar coexistence. Without bipolarity, any complementarity is less fundamental due to the missing “opposites” (Figure 8) [22]. On the other hand, if bipolar equilibrium is the most fundamental form of equilibrium, any multidimensional model such as string and superstring theory or M-theory cannot be most fundamental. In brief, action-reaction, particle-antiparticle, negative-positive energies, input and output, or the

Figure 7. Bohr’s Coat of Arms (Creative Commons file by GJo, 3/8/2010, Source: File: Royal Coat of Arms of Denmark.svg (Collar of the Order of the Elephant) + File: Yin yang.svg).
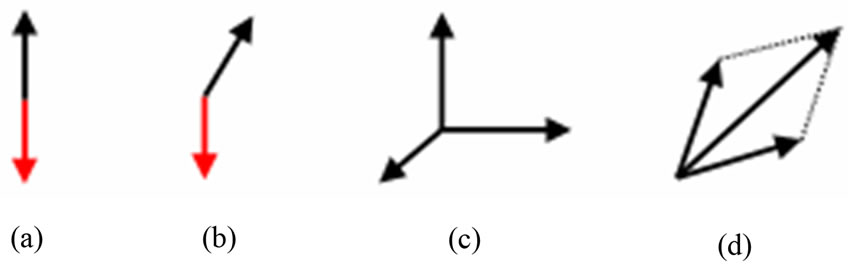
Figure 8. Fundamental and non-fundamental complementarities: (a) Fundamental; (b)-(d) Non-fundamental.
Yin and Yang in general are the most fundamental opposites of nature, but man and woman, space and time, particle and wave, truth and falsity are not exactly bipolar opposites. This could be the reason why Bohr found causal description of a quantum process unattainable and we have to content ourselves with particle-wave complementary descriptions [27]. It may also be the ultimate reason why modern physics so far failed to find a definitive battleground for quantum gravity.
Fundamental and non-fundamental complementarities are illustrated in Figure 8. In this regard, BDL with scientific extensions distinguished itself philosophically from western tradition as well from unscientific Chinese interpretations of YinYang. Theoretically, bipolar complementarity can be posited a basis for YinYang bipolar reciprocal interaction and definable causality. Furthermore, it can be argued that bipolar reciprocal interactions created spacetime and caused all changes in the universe but not vice versa.
Prediction 2. YinYang bipolar causality in the form of BUMP in BDL is the simplest and most fundamental logically definable causality. Without YinYang bipolar complementarity, causality cannot be formally defined with regularity.
Prediction 3. The equilibrium or non-equilibrium states of any physical, biological, social or mental world can be modeled in some way with bipolar quantum logic gates or bipolar quantum cellular combinatorics [22].
Prediction 4. Let y = (y-,y+) = (negative, positive) be a bipolar predicate and a, b, x be any particle-antiparticle or action-reaction bindings or couplings, bipolar quantum entanglement or BUMP is a bipolar equilibrium-based fundamental law governing all types of symmetry and broken symmetry. Formally we have,
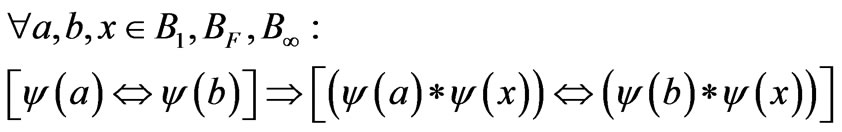
Prediction 5. Should Boson-Fermion symmetry or broken symmetry exist it would be an effect caused by bipolar symmetry or broken symmetry.
Assessment 10 (Philosophy). As God logic, it must unify truth and equilibrium, physics and metaphysics, science and philosophy; it must predict a reincarnation of philosophy that overturns the end or death assertions on philosophy [5,6]. This seems another mission impossible but it is shown accomplishable in Ref. [26], which meets or partially meets the philosophy criterion.
Approximately two centuries ago, Hegel pronounced the end of philosophy. He claimed that his truth-based and contradiction-centered dialectic logic titled The Science of Logic [5] had brought philosophy to its end and there should be no new philosophy after him. AngloAmerican philosophers on the whole, however, found it hard to put up with contradiction while seeking truth. Indeed, contradiction is phenomenon but not the essence of being. The Science of Logic provides neither a formal logic nor the logic of science as Einstein asserted later [11]: “For the time being we have to admit that we do not possess any general theoretical basis for physics which can be regarded as its logical foundation.”
Sir Karl Popper is well-known for his positivist stance in science philosophy and his sharp criticism on dialectics. Popper’s book The Logic of Scientific Discovery argued that science should adopt an empirical methodology based on falsifiability [28]. Popper’s philosophy significantly influenced modern science. Since then, probability theory has been widely regarded as the logic of science. Now it has been used in knowledge-based approaches to science and artificial intelligence. But it can be argued that, although probability is very useful in science, it is not the logic of equilibrium and harmony of what exists. Evidently, probability is not logic. It does not provide logical axiomatization for physics. It uses partial truth without logically definable causality in regularity.
While the end of philosophy was meant by Hegel to be the “top” or “apex”, some scholars went one step further to proclaim the death of philosophy. In The Grand Design, Hawking and Mlodinow declared [6, p5]: “Philosophy is dead” “M-theory predicts that a great many universes were created out of nothing” “Their creation does not require the intervention of some supernatural being or god.” When they advocated M-theory, however, they also promoted the concept of negative and positive energies [6, pp. 179-180] but stopped short of pointing out the unavoidable consequence that the two energies are respectively the Yin and Yang of nature. And when they proclaimed the death of Western philosophy, they are calling back an Eastern philosophy that can lead to a new logic for an equilibrium-based unification of the multiverses in M-theory.
With the unification of truth and equilibrium, science and philosophy are brought together to a supersymmetry of negative-positive energies. This has not been possible without YinYang bipolarity. Philosophically speaking, the metaphysical Being cannot be defined with truthbased logic and cannot provide dynamics for revealing the beings in the real world. As a result, the ultimate Being has been nihilistic in nature characterized with NULL [3]. On the other hand, YinYang bipolarity brings logical dynamics into the equilibrium of being and truth with logically attainable quantum causality.
The above is corroborated by two well-known historical events in quantum mechanics. First, without bipolarity, Niels Bohr used YinYang for particle-wave complementarity but found quantum causality unattainable [27]. Secondly, based on de Broglie’s work, Einstein’s former associate David Bohm proposed a causal interpretation of quantum mechanics [29] but it was branded as “metaphysical” and “ideological”. Einstein initially encouraged Bohm on his work. But, without a different philosophical basis and a new logic, Bohm’s causal interpretation was later dismissed by Einstein as “too cheap” [cf. 30, p. 340]. Evidently, with the logical unification of truth and equilibrium, physics and metaphysics as well as science and philosophy, BDL is no longer merely metaphysical or cheap. After all, it is an equilibrium-based non-linear bipolar dynamic generalization of Boolean logic and all beings including the universe itself must be either an equilibrium or non-equilibrium.
Assessment 11 (Consistency). Although BDL meets or partially meets the first ten criteria, it might be debatable whether it can overturn Gödel’s incompleteness theorems by proving its own consistency within itself. From Table 3 it is clear that, except BUMP, all bipolar axioms are linearly equivalent to its proven sound classical 1st-order counterparts, and BUMP has been proven consistent [12, Ch. 3]. Subsequently, we have:
1. BDL as a supersymmetric logical system subsumes 1st order Boolean logic [12, Ch. 3];
2. The bipolar lattice B1 = {−1,0} ´ {0,+1} as a bounded and complemented version has been extended to the unbounded bipolar lattice Bn = {−n, ∙∙∙, −2, −1, 0} ´ {0, +1, +2, ∙∙∙, +n}, 0 ≤ n ≤ ¥, that subsumes all natural numbers [12, Ch. 4]
3. Bipolar quantum linear algebra (BQLA) defined in B¥ = [−¥,0] ´ [0,+¥] supersets the properties of Peano arithmetic [12,24,25].
It is reported [31, p221] that, the ancient paradox of the liar was the original inspiration for Gödel’s incompleteness theorems. The paradox, which was known even to Aristotle, consists of a single sentence L “This sentence is not true.” If L is true, then L is not true. Thus, L is both true and false. But that is against the fundamental law of non-contradiction. So we have the liar paradox.
Subsequently, a key for an overturn of Gödel’s incompleteness theorems is the elimination of the liar paradox. Evidently, with the bipolar equilibrium-based logical values, BDL does show such elimination. From Figure 2 it is clear that the four values of BDL are equilibrium (−1, +1), non-equilibrium (−1, 0), non-equilibrium (0, +1), and eternal equilibrium (0, 0), where the liar’s paradox is left no room.
Should and can the consistency criterion be satisfied by the candidate as well? The question is left open for further discussion and research effort. This work predicts the following:
Prediction 6: Although Gödel’s incompleteness theorems cannot be overturned by any truth-based logical system, it can be overturned by an equilibrium-based one.
6. Conclusions
The notion of God Logic has been proposed. This notion is to serve as an elicitation for a consistent set of necessary criteria for the logical foundation of Einstein’s grand unification, for revealing the ubiquitous effects of quantum entanglements, and for programming the universe. An evolving set of eleven criteria has been proposed. A supersymmetrical candidate logical system of negativepositive energy dynamic equilibrium has been introduced and assessed against the eleven criteria. It has been shown that the first ten criteria are met or partially met by the candidate. But the question whether the 11th criterion has been or can be met is left open for further discussion and research effort. The assessment has led to a few predictions. Competing ideas, amendments, and falsifications are especially sought.
The notion of God Logic follows Spinoza-Einstein’s philosophical interpretation of God or nature. In contrast to bottom-up approaches to scientific unification such as particle physics or string theory, this work is aimed at developing a holistic logic with a top-down approach for better understanding and interpretation of the orderly harmony of what exists. Hopefully, such understanding can lead to ubiquitous quantum computing, quantum intelligence and enhanced logical, physical, social, mental, and biological equilibrium and harmony, especially nature-man harmony, in human endeavors in the real world [12,32-34].
7. Acknowledgements
The authors acknowledge the reviewers for their valuable comments. This paper used some material from a working book by the first author. With this note, there should be no further copyright clearance for the book’s printing.
REFERENCES
- R. Penrose, “The Road to Reality: A Complete Guide to the Laws of the Universe,” Alfred A. Knopf, New York, 2005.
- S. Lloyd, “Programming the Universe,” Alfred A. Knopf, Inc., New York, 2006.
- L. A. Zadeh, “Causality Is Undefinable—Toward a Theory of Hierarchical Definability,” Proceedings of FUZZ-IEEE, 2001, pp. 67-68
- G. Boole, “An Investigation of the Laws of Thoughts,” MacMillan, London, 1854.
- G. Hegel, “Science of Logic,” Wissenschaft der Logik, tr. George di Giovanni, 2010.
- S. Hawking and L. Mlodinow, “The Grand Design,” Random House Digital, Inc., New York, 2010.
- D. Hilbert, “Mathematical Problems,” Bulletin of the American Mathematical Society, Vol. 8, 1901, pp. 437- 479. http://dx.doi.org/10.1090/S0002-9904-1902-00923-3
- A. Einstein, “The Foundation of the General Theory of Relativity,” Collected Papers of Albert Einstein, English Translation of Selected Texts, Vol. 6, 1916, pp. 146-200.
- K. Gödel, “Über Formal Unentscheidbare Sätze der Principia Mathematica und verwandter Systeme, I.,” Monatshefte für Mathematik und Physik, Vol. 38, 1931, pp. 173-198.
- A. Einstein, “On The Method of Theoretical Physics,” The Herbert Spencer Lecture, Querido Verlag, Amsterdam, 1934.
- A. Einstein, “Considerations Concerning the Fundaments of Theoretical Physics,” Science, Vol. 91, No. 2369, 1940, pp. 487-491. http://dx.doi.org/10.1126/science.91.2369.487
- W.-R. Zhang, “YinYang Bipolar Relativity: A Unifying Theory of Nature, Agents and Causality with Applications in Quantum Computing, Cognitive Informatics and Life Sciences,” IGI Global, Hershey/New York, 2011.
- Fermi National Accelerator Laboratory, “Press Release 06-19,” 2006. http://www.fnal.gov/pub/presspass/press_releases/CDF_meson.html
- W.-R. Zhang and L. Zhang, “YinYang Bipolar Logic and Bipolar Fuzzy Logic,” Information Sciences, Vol. 165, No. 3-4, 2004, pp. 265-287. http://dx.doi.org/10.1016/j.ins.2003.05.010
- W.-R.Zhang, “YinYang Bipolar Lattices and L-Sets for Bipolar Knowledge Fusion, Visualization, and Decision,” International Journal of Information Technology and Decision Making, Vol. 4, No. 4, 2005, pp. 621-645. http://dx.doi.org/10.1142/S0219622005001763
- Y. Shi, V, Seto, L.-S. Chang and V. Shenk, “Transcriptional Repression by YY1, a Human GLI-Kruppel-Related Protein, and Relief of Repression by Adenovirus E1A Protein,” Cell, Vol. 67, No. 2, 1991, pp. 377-388. http://dx.doi.org/10.1016/0092-8674(91)90189-6
- W.-R. Zhang, “Equilibrium Relations and Bipolar Cognitive Mapping for Online Analytical Processing with Applications in International Relations and Strategic Decision Support,” IEEE Transactions on Systems, Man, and Cybernetics, Part B, Vol. 33, No. 2, 2003, pp. 295-307.
- W.-R. Zhang, A. Pandurangi and K. Peace, “YinYang Dynamic Neurobiological Modeling and Diagnostic Analysis of Major Depressive and Bipolar Disorders,” IEEE Transactions on Biomedical Engineering, Vol. 54, No. 10, 2007, pp. 1729-1739. http://dx.doi.org/10.1109/TBME.2007.894832
- W.-R., Zhang, A. Pandurangi, K., Peace, Y. Zhang and A. Zhao, “MentalSquares—A Generic Bipolar Support Vector Machine for Psychiatric Disorder Classification, Diagnostic Analysis and Neurobiological Data Mining,” International Journal on Data Mining and Bioinformatics, Vol. 17, No. 4, 2011, pp. 547-576.
- S. Hawking, “Black Hole Evaporation,” Nature, Vol. 248, 1974, pp. 30-31. http://dx.doi.org/10.1038/248030a0
- S. Hawking, “Particle Creation by Black Holes,” Communications in Mathematical Physics, Vol. 43, No. 3 1975, pp. 199-220. http://dx.doi.org/10.1007/BF02345020
- W.-R. Zhang, “Bipolar Quantum Logic Gates and Quantum Cellular Combinatorics—A Logical Extension to Quantum Entanglement,” Journal of Quantum Information Science, Vol. 3, No. 2, 2013, pp. 93-105. http://dx.doi.org/10.4236/jqis.2013.32014
- W.-R.Zhang, “YinYang Bipolar Fuzzy Sets and Fuzzy Equilibrium Relations for Bipolar Clustering, Optimization, and Global Regulation,” International Journal of Information Technology and Decision Making, Vol. 5, No. 1, 2006, pp. 19-46.
- W.-R. Zhang, H. J. Zhang, Y. Shi and S. S. Chen, “Bipolar Linear Algebra and YinYang-N-Element Cellular Networks for Equilibrium-Based Biosystem Simulation and Regulation,” Journal of Biological Systems, Vol. 17, No. 4, 2009, pp. 547-576.
- W.-R. Zhang,, “YinYang Bipolar Atom—An Eastern Road toward Quantum Gravity,” Journal of Modern Physics, Vol. 3, 2012, pp. 1261-1271. http://dx.doi.org/10.4236/jmp.2012.329163
- W.-R. Zhang, “Beyond Spacetime Geometry—The Death of Philosophy and Its Reincarnation,” Journal of Modern Physics. Vol. 3, 2012, pp. 1272-1284. http://dx.doi.org/10.4236/jmp.2012.329164
- N. Bohr, “On the Notions of Causality and Complementarity,” Dialectica, Vol. 2, No. 3-4, 1948, pp. 312-319. http://dx.doi.org/10.1111/j.1746-8361.1948.tb00703.x
- K. Popper, “The Logic of Scientific Discovery,” Hutchinson & Co., London/New York, 1959.
- D. Bohm, “Causality and Chance in Modern Physics,” by University of Pennsylvania Press, Philadelphia, 1980.
- M. Kumar, “Quantum: Einstein, Bohr, and the Great Debate about the Nature of Reality,” W. W. Norton & Company, New York, 2008.
- R. Rucker, “Mind Tools—The Five Levels of Mathematical Reality,” Houghton Mifflin Company, Boston, 1987.
- W.-R. Zhang, S. Chen and J. C. Bezdek, “A Generic System for Cognitive Map Development and Decision Analysis,” IEEE Transactions on Systems, Man, and Cybernetics, Vol. 19, No. 1, 1989, pp. 31-39. http://dx.doi.org/10.1109/21.24529
- W.-R. Zhang, S. Chen, W. Wang, and R. King, “A Cognitive Map Based Approach to the Coordination of Distributed Cooperative Agents,” IEEE Transactions on Systems, Man, and Cybernetics, Vol. 22, No. 1, 1992, pp. 103-114. http://dx.doi.org/10.1109/21.141315
- D. Y. Gao and H. D. Sherali, “Advances in Applied Mathematics and Global Optimization,” Springer, 2009.

