Open Journal of Antennas and Propagation
Vol.04 No.03(2016), Article ID:70716,20 pages
10.4236/ojapr.2016.43011
Autonomous Wireless Sensors Network Based on Piezoelectric Energy Harvesting
Alex Mouapi, Nadir Hakem, Gilles Y. Delisle
Underground Communication Research Laboratory, University of Québec in Abitibi-Témiscamingue, Val d’Or, Canada

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: August 20, 2016; Accepted: September 18, 2016; Published: September 21, 2016
ABSTRACT
Wireless sensor networks (WSNs) offer an attractive solution to many environmental, security and process monitoring. However, their lifetime remains very limited by battery capacity. Through the use of piezoelectric energy harvesting techniques, ambient vibration can be captured and converted into usable electricity to create self- powering WSN which is not limited by finite battery energy. This paper investigates analytically and experimentally the performance of a WSN powered by a Piezoelectric Energy Harvesting System (PEHS) and a material block-level modeling considering most key energy consumption of a wireless sensor node in a star topology network is proposed. By using real hardware parameters of existing components, the proposed model is used to evaluate the energetic budget of the node. The sensor node performance is evaluated regarding transmit packet size, duty cycle and the number of nodes that can be deployed. From the spectral properties of the available vibration inside two moving vehicles (automobile and train), the maximal recoverable power for each type of vehicle is estimated. Using a PEHS based on a cantilever beam optimized for low-frequency applications, 6 mW power is recovered in the case of the train while a 12.5 mW power is reached in the case of the automobile. It is observed that the sink may not operate with the recovered energy. However, the sensor node can sense and transmit data with a maximum size of 105.5 kbits when the duty cycle is 4 × 10−15. It is also achieved that the node is most effective when the measured physical phenomena vary slowly, such as the variations in temperature due to thermal inertia. Considering an optimized PEHS based on non-linear processing, it is shown that the sink can operate for 190% improvement of the recovered power.
Keywords:
WSN, Self-Powering, PEHS, Packet Size, Duty Cycle, Energy Harvesting System

1. Introduction
In the recent years, energy harvesting techniques are being investigated as a mean to convert unusable forms of energy to electrical energy sufficient to power unattended or inaccessible low power systems [1] . The most targeted application in energy harvesting is the powering of nodes in a WSN [2] [3] ; it is because the nodes life is necessarily linked to that of its storage element (a chemical battery), which either must be replaced or recharged when they become exhausted. This maintenance operation will become increasingly expensive especially when the sensor nodes are deployed in hard to reach places.
The possibility of using ambient energy to increase the lifetime of the sensor nodes is linked to other developments in related technologies such as microelectronics and micromechanics to be used to design ultra-low power sensors nodes with a reasonable cost [4] . Research in using modeling at the protocol layers level to optimize the energy consumption of the node is also very relevant. Much of this work focuses on the Media Access Control (MAC) protocol since it has a significant impact on the energy consumption of the node [5] [6] .
Specifically, energy harvesting consists of gathering freely-available energy from the environment. Several techniques of energy harvesting exist and they differ one from another by the nature of the considered primary energy source. Some of these ambient energy sources are well known now. The sun [7] and the wind [8] , for example, can generate significant energy that can be used on a national grid. At low power levels, however, the sources of energy such as vibration [9] [10] , radio waves [11] , human activity [12] , heat [13] , and the internal light [14] was recently considered as alternative sources to power WSN. Although energy harvesting techniques allow considering immortal sensors nodes, it remains nonetheless that the performance of the sensor node is related to the quantity of recovered energy. This work aims to quantify the performance of a WSN powered by recovered energy from the surrounding ambient sources. The case of vibration sources [9] [10] [15] widely studied in the literature is primarily considered. Previous studies have demonstrated that ambient vibration present in moving vehicles can be harvested and used to generate electrical energy for low power electronics [9] [10] .
In [9] , the authors measured the vibrations induced by the road in an automobile moving at 90 km/h and a maximum power of 3 μW was recovered for an optimal load resistance of 73.13 kΩ. In [10] , a power of 1.1 μW was achieved at optimum load resistance of 91 kΩ. All these researches are only focused on the aim to prove the technical feasibility of WSN supplied by the spurious vibrations in the vehicle. However, the performances of the autonomous WSN based on the recovered energy are not evaluated.
The main objective of this work is then to assess the relevance of such micro generators through the quantification of the performance of a sensor node, powered by vibrational recovered energy. More precisely, the following questions will be addressed throughout this work: the maximum size of data that can be measured regarding available energy; the extent of the network (number of nodes); the type of physical phenomenon that can be measured by the autonomous network and the surface that can be covered by the autonomous network.
To achieve the objectives, a comprehensive energy model considering most key energy consumption of a wireless sensor node in a star topology network is proposed in Section 2. By using the hardware parameters of existing components and commonly used (Chipcorn CC1000 radio [16] and Mica2 Motes wireless measurement system [17] ), the energy budget of the sensor is estimated in the used configuration. In Section 3, the available vibrations are investigated for two types of vehicles: an automobile and a train. The spectral properties of the detected vibrations are then used to assess the maximum recoverable power for each type of vehicle.
Section 4 presents simulations and experimental results about the performances of the piezoelectric powered sensor node and a solution for optimizing the performance of the autonomous WSN is also proposed.
Finally, the conclusion and prospects for this work are presented in Section 5.
2. Wireless Sensor Node Energy Consumption
The general architecture of a wireless sensor node is shown in Figure 1 [18] . Each sensor consists of three main units that must be powered by the PEHS. The sensing unit is the interface to the physical world to conduct the data acquisition. The processing unit is responsible for the treatment of all relevant data and executes the code that describes the behavior of the sensor node. The communication unit is composed of a transmitter/ receiver (radio module) allowing communication between the different nodes of the network. Thus, the sensor node operates if the PEHS is able to supply the other three sensor nodes’ modules: the sensing unit, the processing unit, and the transceiver unit.
Energy consumption in the different modules of a sensor node is linked to the activity of the node in the network [19] . The node operation depends on the topology of the network. There are four main topologies for WSN: star, mesh, hierarchical tree and clustered hierarchical configurations [20] . Depending on the intended application, a topology can be advantageous compared to the other. A comparison of the performance of these topologies is proposed in [20] . In most studies, the choice of a particular topology can be linked to one or other criteria such as self-organizing capability, network life, reliability, energy-efficiency, scalability, data latency, etc. [20] - [22] . This work
Figure 1. Hardware diagram of sensor node.
considers the energy efficiency criterion to choose the network topology to be studied. In [20] , it is shown that for the scenario where the network size is less than the characteristic distance, direct communication in star networks is the most energy efficient. As shown in Figure 2, the star topology consists of a central node (called coordinator or sink of the network) and multiple wireless sensor nodes. In this topology, all sensors nodes send their data directly to the sink. It is assumed that all nodes are homogeneous and will have the same architecture. For simplicity, Time division multiple access (TDMA) protocols are assumed and the energy required for packet acknowledgment is not considered.
As shown in Figure 2, star topology organizes all the peripheral nodes around the sink also called central hub. The sink is logically (and or physically) at the center of the network via direct link [21] . The sink can be either the base station itself or a gateway node that is in direct communication with the base station. In this work, the sink is assumed as a gateway node and it is placed at the center of the network. Thus, all the other nodes are located at the same distance (d) of the sink. Individual sensors are sensing data and transmit to the sink node at a fixed rate. The sink node has to sense the data, receive data from the sensors node, perform data aggregation and transmit the result to the base station. The following Sections 2.1 and 2.2 quantifies the energy dissipated by any node of the network and that dissipated by the sink.
2.1. Sensor Node Energy Consumption
The diagram in Figure 3 can be used to illustrate the activity of the node in the star topology network. As shown in this Figure, the energy consumed by a sensor node can be attributed to four basic energy consumptions: the dissipated energy during sensing, during transmission to sink node, microcontroller processing energy and the transient energy. Energy for actuation also exists but it is difficult to estimate this residual energy in general because this depends heavily on the application [19] . In this work, this dissipation source is not considered.
The sensing system is the interface to the physical world to carry out the acquisition of the data. In [19] , the total energy for the acquisition of data (namely,  for b bits per packet) includes energy dissipated during the data capture
for b bits per packet) includes energy dissipated during the data capture  and
and
Figure 2. Star topology with eight sensor nodes.
Figure 3. Sensor node behavior.
energy for data recording in the memory . The relationship between these energies is represented as follows:
. The relationship between these energies is represented as follows:
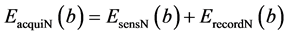 (1)
(1)
with:
 (2)
(2)
All the parameters used to assess the energy consumption of the sensor node are defined in Table 1.
The energy consumed during the transmission of the data depends on the size of the transmitted data (b), the sink-node distance (d) and the path loss exponent n. To send a b-bit packet at a distance d, the dissipated energy is defined by [23] :
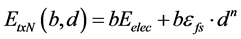 (3)
(3)
where n is the distance based path loss exponent [24] . In this work, 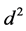 energy loss is accepted for the transmission between the sensor node and the sink.
energy loss is accepted for the transmission between the sensor node and the sink.
The energy for processing and aggregation of the data mainly consumed by the micro- controller 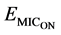 is attributed to two components: energy loss from switching
is attributed to two components: energy loss from switching 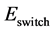 and energy loss due to leakage current
and energy loss due to leakage current 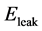 [19] . It is defined in [23] as:
[19] . It is defined in [23] as:
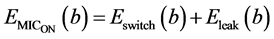 (4)
(4)
with:
 (5)
(5)
Table 1. Parameter values used to estimate energy consumption of Sensor Node.
During the operation of a sensor node, a certain amount of energy is dissipated due to the transition between the different states of the node elements (active, idle or sleep). The most relevant parts are the radio module and the MC (Micro Controller) unit. In [22] , the transient energy in the sensor node is defined by:
 (6)
(6)
 is the duty cycle of the sensor node expressed as:
is the duty cycle of the sensor node expressed as:

The sleep time for our research varies with
Considering Equations (1), (3), (4) and (6), the total energy dissipated by the sensor node 

Figure 4 shows the total dissipated energy in the node as a function of the sink-node distance.
It appears that the sink-node distance has very little influences the energy dissipated by the node. It is practically constant up to the distance of 8 m. This can be explained by the low dissipation value in free space. In this work, the value of 10 pJ/(bit/m2) is used [19] .
2.2. Sink Node Energy Model
The activity of the sink is much denser. The different steps performed during one cycle are shown in the diagram of Figure 5. The energy consumed by the sink can be attributed to five energy consumption sources: the dissipated energy during sensing, during data reception, during data processing, during transmission to the base station and the transient energy.
The energy dissipated during the data capture is the same as that of a classical node, namely:

In [23] , the energy expended to receive b-bit packet is defined as:
Figure 4. Node energy dissipation versus sink-node distance.
Figure 5. Sink Sensor node behavior.

where N is the total number of the sensor nodes.
The energy for processing and aggregation of the data in the case of sink is defined as [23] :

Energy dissipation due to transmission of the 


A 
As in the case of the classical node, the dissipated energy by the sink due to the change of state is defined by:

where 



where 




Figure 6. Wake-up and sleeping times of the sensor nodes and the sink node per cycle.

In Figure 6, 

The total energy consumed by the sink node per round is expressed as:

The energy dissipated by the sink is therefore determined by the number of nodes and the sink to the base station distance. Figure 7 shows the energy dissipated depending on the number of nodes. It is shown that the dissipated energy increases with the number of nodes. However, the dissipated energy varies very little for sink-base station distance less than 400 m. The WSN can then be deployed at this distance from the base station without great consequence on the consumed energy. The next section, the properties of the measured vibrations is used to evaluate the performance of the WSN.
3. Vibrations in Vehicles
3.1. Vibrational Harvester Model
The most popular piezoelectric generators are the cantilever structure which is very effective for low-frequency applications [9] [10] . The geometry of the cantilever beam proposed in [28] is shown in Figure 8.
The piezoelectric beam comprises three main parts: the composite beam, the seismic mass, and the piezoelectric layers. The cantilever beam is used to amplify the relative displacement of the seismic mass to the displacement amplitude of the vibration source. The seismic mass increases the mechanical stress applied to the piezoelectric material, thus producing a high output power. The piezoelectric composite which is the active part of the structure is used to convert mechanical vibrations into electrical energy.
The alternative power generated by the piezoelectric transducer denoted in Figure 8, is shown regarding the RMS power transferred to the resistive load as follows [28] :

Figure 7. Dissipated energy depending on the distance.
Figure 8. Piezoceramic cantilever beam [28] .
where 

with:

Regarding the cantilevers’ beams, some optimizations have been proposed. For example, a multi harvesting structure (using multiple beams) was envisaged [29] . It certainly helps to increase the bandwidth of the generator but also to enhance the size of the recovery system, which makes it cumbersome for our application. Hence, in this work, the cantilever beam is considered in its simplest structure. The parameters’ values used to compute Equation (17) are listed in Table 2 with the references where these values are originated.
Equation (17) shows that the recoverable power depends on the properties of the detected vibrations

Table 2. Properties of the piezoelectric transducer based on PZT-5H [28] [30] [31] .
node operating cycle can be defined by:

where 

Figure 9 shows the influence of the recovered power on the performance of the autonomous sensor node. By using the measured vibration data, given in [31] , Figure 9 shows the performance of the node regarding sizes of packets transmitted and k represents the ratio between the sleep and the active times (
・ 
・ 
・ 
Figure 9. Transmit packets’ size based on the recovered energy. Analytical results for 


every 100 s; the maximum packet size, in this case, is 451 bits.
・ 
In the next section, the spectrum of actual, detected vibrations in two types of vehicle are investigated.
3.2. Detected Vibration and Maximum Recoverable Power
To measure ambient vibrations, an ACC103 laboratory accelerometer has been used. It has an output of 
Taking into account previous work in which the maximum frequency observed was 28 Hz [32] , the data are samples at 100 Hz and MATLAB's Fast Fourier Transform (FFT) software was then used to obtain frequency analysis. The data acquisition scheme is that shown in Figure 11.
Two vehicles are considered in this work. A Kia Spectra brand automobile which has run about 126,000 km is used and a Canadian transport company (VIA Rail Canada) train. Many sets of measurements were made during the Montreal-Ottawa round trip (about 450 km) in the case of the train. More than 14,700 samples were taken. The results obtained for the car are shown in Figure 12.
Figure 10. Measurement equipment.
Figure 11. Vibration measurement scheme.
Figure 12. Vibration spectrum in automobile.
In Figure 12, an acceleration peak of 1.5 g is observed of the neighboring of 37 Hz. This result is close to that obtained in [31] which was 1.4 g. Two series of measurements are also shown in the case in Figure 13. A small difference is observed between acceleration intensity measurements depending on train operating speed, which varied from one set of measurements to another. In this work, an average
Figure 13. Vibration spectrum train.
frequency of 26 Hz is taken for an average peak acceleration of 0.55 g. This main frequency stays pretty close to the 28 Hz obtained in [32] .
Using the spectral properties of the measured vibration and Equations (17)-(19), a representation of the power dissipated in a resistive load for both types of vehicles is shown in Figure 14. A maximum power of 12.49 mW is reached for the case of the automobile while 6 mW can be recovered in the case of the train. This is because measurement in the automobile is made directly on the engine.
4. WSN Performances Powered by Piezoelectric Recovered Energy
In this section, Matlab simulations are used to evaluate the performance of the WSN. By using the maximum recoverable power, performance regarding transmitted packets size and the number of nodes for both vehicles are assessed. Given the small amount of available energy, the case of situations where measures may be made every 17 minutes were considered. Since

Figure 15 shows the node’s performance and that of the sink for both types of vehicles. The curves demonstrate that the energy allows considering the transmission of data with a maximum size of 105.5 kbits for each node. However recovered energy is not sufficient for energy needs of the sink, making it impossible to consider the operation of the entire network.
In the field of design of cantilever beams, it has been shown that non-linear techniques can increase the electromechanical coupling and therefore at the same time the recovered energy [33] . The best known nonlinear method is the Synchronized Switch Harvesting on Inductor (SSHI) [34] . The behavior of the cantilever beam be-
Figure 14. Maximum recoverable power from measured vibration.
Figure 15. Performances of WSN based on recovered energy N = 5.
ing capacitive, the method consists of the addition in parallel of an inductance so as to form an oscillating system for amplifying the output power (Figure 16).
As shown in Figure 16, SSHI technique involves the addition of a switching device in parallel with the piezoelectric element. Switching is done at the time for which, the displacement of the vibrating structure is maximum. At these times, the voltage of the piezoelectric generator is also at its peak. Once the switch is closed, the system consisting of the cantilever beam and the inductor forms a pseudo-peri- odic oscillating system. The difficulty in the application of this technique lies in the design of the switching circuit [35] . This issue is not addressed in this work. In [35] , experimental measurements performed on a cantilever beam show that the SSHI
Figure 16. Nonlinear piezoelectric cantilever beam.
technique allows a 160% increase of the harvested power compared to a standard energy harvesting circuit. Figure 17 indicates that it takes an amplification of 1.9 times the recovered energy to consider the operation of the network with data size up to 3.5 kbits.
The relationship, between the number of nodes that can be deployed and the required gain is shown in Table 3. The number of sensor nodes in the network is varied and measuring the gain necessary for the transmission of data with packet size of 2 kbits is made. The results show that a 52.2% improvement of the gain allows considering an extension of the network from 1 to 30 sensor nodes.
5. Conclusions
In this work, the performance of an autonomous WSN based on vibrational recovered energy has been studied, both numerically and experimentally. A comprehensive energy model of a sensor node, in the star topology network, is proposed and used to assess the energy budget of the node. The proposed energy consumption model is used to assess the power consumption of the sensor node. Using the parameters of existing components, it has been shown that the nodes can be deployed in an area of 200 m2 (each node being located 8 m from the sink). It is also observed that the network can be located up to 400 m from the base station.
Measurements of vibrations in two types of vehicles (automobile and train) are used to assess the maximum recoverable power. This maximum recoverable power is evaluated by using an optimized cantilever beam for low frequencies applications. Based on the measured vibrations, it is shown that powers of 12.5 mW and 6 mW can be recovered in the automobile and train respectively. This available power allows considering nodes that can measure and transmit data with a maximum size of 105 kbits, when the measurements can are taken every 17 min. However, the energy available does not allow the operation of the sink. Considering an amplification of 1.9 times the power recovered using nonlinear techniques, it is observed that the WSN can operate with a maximum capacity of 3.5 kbits when 5 nodes are deployed
Figure 17. Sink node performances after SSHI optimization.
Table 3. SSHI gain versus number of nodes (b = 2 kbits).
around the sink. The method proposed in this work can be used to enslave a network to any ambient recoverable energy.
Although the method proposed in this work allows considering a sensor node enslaved to ambient vibrations, it would be boring to design a backup power supply for powering the node in the event of a malfunction of the vibration source (motor stop for example). The use of a hybrid micro generator (several sources of primary energy) would make robust the recovery system.
Cite this paper
Mouapi, A., Hakem, N. and Delisle, G.Y. (2016) Autonomous Wireless Sensors Network Based on Piezoelectric Energy Harvesting. Open Jour- nal of Antennas and Propagation, 4, 138- 157. http://dx.doi.org/10.4236/ojapr.2016.43011
References
- 1. Hamilton, M.C. (2012) Recent Advances in Energy Harvesting Technology and Techniques. 38th Annual Conference on IEEE Industrial Electronics Society, Montreal, 25-28 October 2012, 6297-6304. http://dx.doi.org/10.1109/iecon.2012.6389019
- 2. Sim, Z.W., Shuttleworth, R., Alexander, M.J. and Grieve, B.D. (2010) Compact Patch Antenna Design for Outdoor RF Energy Harvesting in Wireless Sensor Networks. Progress in Electromagnetics Research, 105, 273-294. http://www.jpier.org/pier/pier.php?paper=10052509 http://dx.doi.org/10.2528/PIER10052509
- 3. Basagni, S., Naderi, M.Y., Petrioli, C. and Spenza, D. (2013) Wireless Sensor Networks with Energy Harvesting. In: Basagni, S., Conti, M., Giordano, S. and Stojmenovic, I., Eds., Mobile Ad Hoc Networking: The Cutting Edge Directions, John Wiley and Sons Inc., Hoboken, 701-736. http://dx.doi.org/10.1002/9781118511305.ch20
- 4. Polastre, J., Robert, S. and David, C. (2005) Telos: Enabling Ultra-Low Power Wireless Research. IEEE International Symposium on Information Processing in Sensor Networks, Los Angeles, 15 April 2005, 364-369.
- 5. Yongsheng, S.H.I. and Gulliver, T.A. (2009) An Energy-Efficient MAC Protocol for Ad Hoc Networks. Wireless Sensor Network, 1, 407-416. http://dx.doi.org/10.4236/wsn.2009.15049
- 6. Haifang, F., Lixiang, M. and Supeng, L. (2010) A Low Overhead Wireless Sensor Networks MAC Protocol. IEEE International Conference on Computer Engineering and Technology (ICCET), Chengdu, 16-18 April 2010, 128-131. http://dx.doi.org/10.1109/iccet.2010.5485683
- 7. Win, K.K., Wu, X., Dasgupta, S., Wen, W.J., Kumar, R. and Panda, S.K. (2010) Efficient Solar Energy Harvester for Wireless Sensor Nodes. IEEE International Conference on Communication Systems, Singapore, 17-19 November 2010, 289-294.
- 8. Tan, Y.K. and Panda, S.K. (2011) Self-Autonomous Wireless Sensor Nodes with Wind Energy Harvesting for Remote Sensing of Wind-Driven Wildfire Spread. IEEE Transactions on Instrumentation and Measurement, 60, 1367-1377. http://dx.doi.org/10.1109/TIM.2010.2101311
- 9. Mouapi, A., Hakem, N., Delisle, G.Y. and Kandil, N. (2015) A Novel Piezoelectric Micro-Generator to Power Wireless Sensors Networks in Vehicles. IEEE International Conference on Environment and Electrical Engineering, Rome, 10-13 June 2015, 1089-1092.
- 10. Qingyuan, Z., Mingjie, G. and Yuanqin, H. (2012) Vibration Energy Harvesting in Automobiles to Power Wireless Sensors. International Conference on Information and Automation, Shenyang, 6-8 June 2012, 349-354.
- 11. Haboubi, W., Takhedmit, H., Lan Sun Luk, J.D., Salah-Eddine, A., Allard, B., Costa, F., Vollaire, C., Picon, O. and Cirio, L. (2014) An Efficient Dual-Circularly Polarized Rectenna for RF Energy Harvesting in the 2.45 GHz ISM Band. Progress in Electromagnetics Research, 148, 31-39. http://dx.doi.org/10.2528/PIER14031103
- 12. Chuo, Y., Marzencki, M., Hung, B., Jaggernauth, C., Tavakolian, K., Lin, P. and Kaminska, B. (2010) Mechanically Flexible Wireless Multisensor Platform for Human Physical Activity and Vitals Monitoring. IEEE Transactions on Biomedical Circuits and Systems, 4, 281-294. http://dx.doi.org/10.1109/TBCAS.2010.2052616
- 13. Jacquot, A., Chen, G., Scherrer, H., Dauscher, A. and Lenoir, B. (2005) Improvements of On-Membrane Method for Thin Film Thermal Conductivity and Emissivity Measurements. Sensors and Actuators, 117, 203-210. http://dx.doi.org/10.1016/j.sna.2004.06.013
- 14. Fraas, L.M., Avery, J.E. and Nakamura, T. (2002) Electricity from Concentrated Solar IR in Solar Lighting Applications. IEEE Photovoltaic Specialists Conference, Louisiana, 19-24 May 2002, 963-966. http://dx.doi.org/10.1109/pvsc.2002.1190758
- 15. Roundy, S., Wright, P.K. and Rabaey, J. (2003) A Study of Low Level Vibrations as a Power Source for Wireless Sensor Nodes. Computer Communications, 26, 1131-1144. http://dx.doi.org/10.1016/S0140-3664(02)00248-7
- 16. Chipcon CC1000 Datasheet. http://www.ti.com/lit/ds/symlink/cc1000.pdf
- 17. MICA2 Mote Datasheet. http://www.datasheetarchive.com/mica2-datasheet.html
- 18. Akyildiz, I.F., Weilian, S., Sankarasubramaniam, Y. and Cayirci, E. (2002) A Survey on Sensor Networks. IEEE Communications Magazine, 40, 102-114. http://dx.doi.org/10.1109/MCOM.2002.1024422
- 19. Halgamuge, M.N., Malka, N., Zukerman, M. and Romamohanarao, K. (2009) An Estimation of Sensor Energy Consumption. Progress in Electromagnetics Research B, 12, 259-295. http://dx.doi.org/10.2528/PIERB08122303
- 20. Shrestha, A. and Xing, L. (2007) A Performance Comparison of Different Topologies for Wireless Sensor Networks. IEEE Conference on Technologies for Homeland Security, Woburn, 16-17 May 2007, 280-285. http://dx.doi.org/10.1109/ths.2007.370059
- 21. Sadouq, Z.A., Mabrouk, M.E. and Essaaidi, M. (2014) Conserving Energy in WSN through Clustering and Power Control. IEEE International Colloquium in Information Science and Technology, Tetouan, 20-22 October 2014, 402-409. http://dx.doi.org/10.1109/cist.2014.7016654
- 22. Miller, M.J. and Vaidya, N.H. (2005) A MAC Protocol to Reduce Sensor Network Energy Consumption Using a Wakeup Radio. IEEE Transactions on Mobile Computing, 4, 228- 242. http://dx.doi.org/10.1109/TMC.2005.31
- 23. Wang, A. and Chandrakasan, A. (2002) Energy-Efficient DSPs for Wireless Sensor Networks. IEEE Signal Processing Magazine, 19, 68-78. http://dx.doi.org/10.1109/MSP.2002.1012351
- 24. Rappaport, T.S. (1996) Wireless Communications: Principles and Practice. 2nd Edition, Prentice Hall, Upper Saddle River.
- 25. Shnayder, V., Hempstead, M., Chen, B., Allen, G.W., and Welsh, M. (2004) Simulating the Power Consumption of Large-Scale Sensor Network Applications. Proceedings of the 2nd International Conference on Embedded Networked Sensor Systems, New York, 3-5 November 2004, 188-200. http://dx.doi.org/10.1145/1031495.1031518
- 26. Heinzelman, W.R., Chandrakasan, A. and Balakrishnan, H. (2000) Energy-Efficient Communication Protocol for Wireless Microsensor Networks. Proceedings of the 33rd Annual International Conference on System Sciences, Hawaii, 4-7 January 2000, 3005-3014. http://dx.doi.org/10.1109/HICSS.2000.926982
- 27. Heinzelman, W.R., Sinha, A., Wang, A. and Chandrakasan, A.P. (2000) Energy-Scalable Algorithms and Protocols for Wireless Microsensor Networks. IEEE International Conference on Acoustics, Speech, and Signal Processing, Istanbul, 5-9 June 2000, 3722-3725. http://dx.doi.org/10.1109/icassp.2000.860211
- 28. Roundy, S. and Paul, K.W. (2004) A Piezoelectric Vibration Based Generator for Wireless Electronics. Smart Materials and Structures, 13, 1131-1142. http://dx.doi.org/10.1088/0964-1726/13/5/018
- 29. Shahruz, S.M. (2006) Design of Mechanical Band-Pass Filters for Energy Scavenging. Journal of Sound and Vibration, 292, 987-998. http://dx.doi.org/10.1016/j.jsv.2005.08.018
- 30. Beeby, S.P., Tudor, M.J. and White, N.M. (2006) Energy Harvesting Vibration Sources for Microsystems Application. Measurement Science and Technology, 17, R175-R195. http://dx.doi.org/10.1088/0957-0233/17/12/r01
- 31. Beeby, S.P., Wang, L., Zhu, D., Weddell, A.S., Merrett, G.V., Stark, B. and Al-Hashimi, B.M. (2013) A Comparison of Power Output from Linear and Nonlinear Kinetic Energy Harvesters Using Real Vibration Data. Smart Materials and Structures, 22, Article ID: 075022. http://dx.doi.org/10.1088/0964-1726/22/7/075022
- 32. Song, D., Yang, C.H., Hong, S.K., Kim, S.B., Woo, M.S. and Sung, T.H. (2012) Feasibility Study on Application of Piezoelectricity to Convert Vibrations of Korea Train Express. Proceedings of ISAF-ECAPD-PFM, Aveiro, 9-13 July 2012, 1-4. http://dx.doi.org/10.1109/isaf.2012.6297738
- 33. Richard, C., Guyomar, D., Audigier, D. and Ching, G. (1999) Semi-Passive Damping Using Continuous Switching of a Piezoelectric Device. Symposium on Smart Structures and Materials, Newport Beach, 1-5 March 1999, 104-111. http://dx.doi.org/10.1117/12.349773
- 34. Barton, D.A.W., Stephen, G.B. and Lindsay, R.C. (2010) Energy Harvesting from Vibrations with a Nonlinear Oscillator. Journal of Vibration and Acoustics, 132, Article ID: 021009. http://dx.doi.org/10.1115/1.4000809
- 35. Lallart, M. and Guyomar, D. (2008) An Optimized Self Powered Switching Circuit for Non- Linear Energy Harvesting with Low Voltage Output. Smart Materials and Structures, 17, Article ID: 035030. http://dx.doi.org/10.1088/0964-1726/17/3/035030



















