Open Journal of Statistics
Vol.07 No.01(2017), Article ID:74082,18 pages
10.4236/ojs.2017.71004
An Application of Heterogeneous Bayesian Regression Models with Time Varying Coefficients to Explore the Relationship between Customer Satisfaction and Shareholder Value
Duncan K. H. Fong1, Qian Chen1, Zhe Chen2, Rui Wang3
1Department of Marketing, Pennsylvania State University, University Park, USA
2Department of Statistics, Pennsylvania State University, University Park, USA
3Department of Marketing, Peking University, Beijing, China

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: November 10, 2016; Accepted: February 10, 2017; Published: February 13, 2017
ABSTRACT
The authors propose new Bayesian models to obtain individual-level and time-varying regression coefficients in longitudinal data involving a single observation per response unit at each time period. An application to explore the association between customer satisfaction and shareholder value is included in the paper. The Bayesian models allow the flexibility of incorporating industry and firm factors in the context of the application to help explain variations of the regression coefficients. Results from the analysis indicate that the effect of customer satisfaction on shareholder value is not homogeneous over time. The proposed methodology provides a powerful tool to explore the relationship between two important business concepts.
Keywords:
Bayesian Analysis, Dynamics, Heterogeneity, Customer Satisfaction, Shareholder Value

1. Introduction
Fong, Ebbes and DeSarbo [1] have proposed a heterogeneous Bayesian regression model in 2012 that enables the estimation of individual-level regression coefficients in cross-sectional data involving a single observation per response unit. This paper extends their work to deal with longitudinal data by developing Bayesian models that provide individual-level and time-varying regression coefficients. As an application, the proposed Bayesian models are used to investigate the relationship between customer satisfaction and shareholder value. Note, it has been one of the fundamental findings of marketing theory that customer satisfaction will benefit firm performance [2] - [11] . Therefore, it is of tremendous interest to explore the potential dynamic and heterogeneous natures of the association between customer satisfaction and shareholder value.
Some scholars have recently started to investigate whether the effect of customer satisfaction on shareholder value is homogeneous across all firms/indus- tries. Several studies reported that the effect of customer satisfaction on shareholder value is heterogeneous across all firms/industries. The authors of those studies performed regression analysis assuming individual-level regression coefficients and their results indicated that there were substantive differences on the coefficients from industry to industry [12] as well as from firm to firm [12] [13] [14] . The effect of customer satisfaction was quite significant to some firms/in- dustries, while it was less valuable or even ignorable to the others, such as the hospitality and tourism industry [11] . However, few studies have examined whether the relationship is temporally labile. Indeed, a common underlying assumption is that the relationship is time-invariant. Yet, it is plausible that the relationship shifts over time. Thus, this reveals an imperative need for developing a model that allows for cross-sectional heterogeneity and temporal dynamics simultaneously.
The proposed Bayesian models provide individual-level and time-varying regression coefficients which also allow the incorporation of firmographic variables to help explain variations in the coefficients. Graphically speaking, when fitting an aggregate-level regression model, as shown in Figure 1(a), there is only one common regression coefficient for all firms over time, ignoring either individual heterogeneity or dynamics. The Bayesian random-effect model (e.g., [15] [16] ) can be used to obtain individual-level coefficient estimates but it assumes that the coefficient for each individual firm is constant over time, as shown in Figure 1(b). Liechty, Fong, and DeSarbo [17] attempt to address this issue by modeling each of such coefficients as the sum of an aggregate-level time-de- pendent coefficient and an individual level random coefficient. Yet, their assumption may be restrictive because the pattern of variation for the coefficients over time is then the same for all firms; in other words, their model is applicable only when the pattern as depicted in Figure 1(c) is assumed to hold. Clearly, it does not allow the regression coefficients for different firms to vary differently over time as shown in Figure 1(d), which is a more general case. Note that DeSarbo et al.’s model proposed in 2012 [18] allows individual level and time varying regression coefficients but their model lacks flexibility in that impact of firm and industry factors on the association cannot be easily incorporated. In this paper, two heterogeneous Bayesian regression models are developed to investigate the association between customer satisfaction and shareholder value which can articulate the dynamic heterogeneity as shown in Figure 1(d). Also, the proposed Bayesian models are flexible which allow the incorporation of industry
Figure 1. Different models on the relationship between customer satisfaction and shareholder value1.
and firm factors to help explain variations of the association.
In short, this study aims to develop new heterogeneous Bayesian regression models to explore the relationship between two important business concepts, namely, customer satisfaction and shareholder value. The findings can be useful to firms in plotting their own marketing strategies. The remainder of this paper is organized as follows. Section 2 describes how the data are collected and the operationalization of the measurements that are used in the study. Section 3 presents a traditional regression analysis following the practice of previous literature. Section 4 presents the proposed Bayesian models in details. Section 5 summarizes the model results as well as findings. Section 6 concludes with a discussion and possible extensions of the proposed models.
2. Data and Measures
We collect a longitudinal data set (from 1998 to 2007) from multiple archival sources to perform our empirical study. For the measure of customer satisfaction (SAT), we use the American Customer Satisfaction Index provided by the ACSI database, which has been successfully employed by a growing body of marketing researchers (e.g., [12] [19] [20] ). This index is reported on a 0 to 100 scale. Given a time lag was found previously between customer satisfaction and its influence on shareholder value in several studies [20] [21] , we actually employed the American Customer Satisfaction Index from 1998 to 2006 in the study while shareholder values were collected from 1999 to 2007. Also, consistent with previous studies, we removed utilities firms as well as privately held companies from our data [20] . The final data set then contains 70 firms with 630 observations of customer satisfaction measurements.
Consistent with the literature, we select Tobin’s q [22] to measure shareholder value for the 70 firms. Note that, with the advantage of being forward-looking and comparable across industries, Tobin’s q receives wide acceptance in the economics and finance literature. We employ the method given in Chung and Pruitt’s paper [23] to compute Tobin’s q at the annual basis, using data from COMPUSTAT from 1999 to 2007. We take the natural logarithm on Tobin’s q, denoted by , to eliminate a violation of normality assumption in our subsequent analysis.
In addition, we include a number of firm and industry factors to help explain the variation in the customer satisfaction and shareholder value association. For firm factors, following Morgan and Rego’ work in 2006 [20] , we obtain measures on firm asset (AS), firms’ relative advertising intensity (AD) and Research and Development intensity (RD) using data from COMPUSTAT. Here firm asset is used as a proxy for firm size, which represents possible scale economies that may impact firm performance. Firms’ advertising and R&D intensities are computed by dividing advertising and R&D expenditure, respectively, by sales. To capture industry dynamism, we consider market concentration and demand growth in our analysis. The widely used indicator, Herfindahl-Hirschman index (HHI), is chosen as the measure of market concentration [12] [20] which is calculated as the sum of the squares of all suppliers’ market shares in an industry. We use the 4-digit SIC code available from COMPUSTAT to categorize the industries. The value of HHI is then scaled to lie between zero (less concentrated) and one (highly concentrated). Finally, following Morgan and Rego [20] , we compute the average 12-month growth in industry sales as a measure of demand growth (DG). The operationalization of various measures is given in Appendix A.
The descriptive statistics for the variables in our data set for each of the nine years are presented in Table 1. Aside from Q, the explanatory variables are on very different scales. For example, the mean of AS is approximately 10, but the mean of AD is only around 0.05. To eliminate the possibility that the effects of smaller-scaled variables are obscured by larger-scaled variables, we standardized all explanatory variables in our study.
3. A Traditional Analysis
Following the literature (e.g., [12] [20] ), we first postulate an aggregate-level regression model using data from our data set to study the association between customer satisfaction and shareholder value. We specify the following model:
(1)
where
・ Qi,t (logarithm of Tobin’s q) denotes the shareholder value for firm , in year ,
・ SATi,t−1 denotes customer satisfaction measured by American Customer Satisfaction Index (ACSI) for firm i in year t − 1,
Table 1. Descriptive statistics of variables in the data set.
・ ASi,t−1 denotes firm asset for firm i in year t − 1,
・ ADi,t−1 denotes firm i’s relative advertising intensity in year t − 1,
・ RDi,t−1 denotes firm i’s relative Research and Development intensity in year t − 1,
・ DGi,t−1 denotes demand growth for firm i in year t − 1,
・ HHIi,t−1 denotes market concentration for firm i in year t − 1,
・ β0 denotes intercept,
・ denote corresponding regression coefficients,
・ ɛi,t denotes the error term which follows a Normal distribution.
Table 2 summarizes the model results. As expected, the estimate of the regression coefficient of SAT is significant and positive, consistent with findings from similar studies in the literature. We have also analyzed the data on a yearly basis for each of the nine year. We obtain significant regression results for each year with R2 ranging from 0.289 to 0.476 and estimates of the regression coefficient of customer satisfaction ranging from 0.132 to 0.225. These results further confirm an overall positive relationship between shareholder value and customer satisfaction.
4. The Proposed Bayesian Models
4.1. The Heterogeneous Bayesian Regression Model 1 (HBRM1)
To investigate the dynamic relationship between customer satisfaction and shareholder value, we first consider a Bayesian version of the aggregate-level regression model but in a more general form, assuming that:
(2)
Table 2. Results of the aggregate regression analysis.
***p < 0.01.
and for j = 0, 1,
(3)
where denote the impact coefficients of the various firm and industry factors on the customer satisfaction and shareholder value association and is the intercept. Note that, when , Equations (2) and (3) can be combined to yield an aggregate-level regression model with common regression coefficients across all firms.
For ease of presentation, we rewrite the model (HBRM1) specification in matrix notations. Let Xit be a column vector with one as the first element and the ith firm’s customer satisfaction score (SAT) at time t − 1 as the second element:
(4)
(5)
where Zit is a K × 1 vector of firm and industry factor values at time t − 1 with the first element set at 1, and Δ is a J × K matrix of impact coefficients. The error terms ɛit and δit are independent and normally distributed with ɛit~ N(0, σ2) and δit~NJ(0, Σ) . In particular, we let Σ = σ2C which is commonly assumed in Bayesian dynamic linear models [24] . Note that, when there is only 1 observation per firm (T = 1), this model reduces to the one considered in Fong, Ebbes and DeSarbo’s work in 2012 [1] . To complete the model specification, we assume the conventional proper priors for the following parameters:
(6)
(7)
(8)
where Gamma(p,q) represents a Gamma distribution with mean pq and variance pq2, WJ(ν,V) denotes a Wishart distribution with mean νV, and vec(Δ) converts Δ into a vector by stacking the rows of Δ on top of one another.
With proper priors, the joint posterior distribution is proper and one can obtain posterior estimates of various parameters of interest. An efficient Gibbs sampler is used to generate random deviates of the parameters iteratively and recursively from the full conditional distributions as listed below. Appendix B provides details of the derivation.
・ p(βit|all others) is a multivariate Normal distribution, for and .
・ p(η|all others) is a multivariate Normal distribution, where η = vec(Δ).
・ p( |all others) is a Gamma distribution.
・ p( |all others) is a Wishart distribution.
4.2. The Heterogeneous Bayesian Regression Model 2 (HBRM2)
In this model we allow impacts of firm and industry factors on the association between customer satisfaction and shareholder value to vary over time. Also, the error variances may vary over time. Therefore we proposed the following heterogeneous Bayesian regression model (HBRM2):
(9)
(10)
where Δt is a J × K matrix of impact coefficients at time t. The error term eit follows N(0, ) independently and the error term fit follows NJ(0, Σt) independently. Again, we let Σt = , where Ct is a scale-free matrix.
As observations are taken over time, we assume the prior distribution of the time varying impact coefficients and variances at time t depends on the prior of the parameters at t ? 1 as well as the previous observed data:
・ At Year 1 (t = 1), similar to HBRM1, we assume the following proper priors for the parameters:
(11)
(12)
(13)
・ However, at subsequent years (t > 1), we use the posterior distribution of the parameters from time t ? 1 as the prior distribution of the relevant parameters at time t. Specifically, let be the information known at time t for firm i, and Di,0 be the information available at time zero, t hen the prior distribution of , is:
(14)
where pt−1 represents the posterior distribution of the parameters at time t − 1. An advantage of this prior specification is that we only make a prior assumption at time t = 1 without the need of introducing further subjective prior input afterwards. Note that such derived priors are informative priors. In the special case where these parameters are not time varying, this model becomes HBRM1.
We develop an MCMC algorithm to simulate random deviates of the parameters iteratively and recursively from the full conditional distributions as listed below. Details of the derivation are provided in Appendix C.
・ p(βit|all others) is a multivariate Normal distribution, for and .
・ p(ηt|all others) is a multivariate Normal distribution, where , for t = .
・ p( |all others) is a Gamma distribution, for .
・ p( |all others) is a Wishart distribution for t = 1 but a non-standard probability distribution for .
We can generate random deviates directly from the full conditional distributions for βit, ηt, , , and . For (t > 1), the corresponding full conditional distributions are not standard probability densities, so we use the Metropolis-Hasting algorithm to generate the random deviates. More sampling details are described in Appendix C.
5. Results from the Bayesian Analysis
We use an uninformative prior in our HBRM1 analysis by specifying p = 3, q = 1, γ = 10IJK, V = IJ, and ν = J + 10. Then, we use results from HBRM1 to specify priors at time t = 1 for HBRM2. To assess the effect of customer satisfaction on the shareholder value, we compute the posterior probabilities of the SAT coefficients (βi,t,1) being positive (cf., [25] ). Figure 2(a) and Figure 2(b) show the posterior probabilities derived from the proposed models, respectively, where, for each year, firms are arranged in an ascending order of posterior probability. The figures clearly show that, given any year, not all firms have high probabilities of possessing positive association between customer satisfaction and shareholder value. Indeed, some firms have noticeable low probabilities suggesting a negligible positive association. Thus, it appears that customer satisfaction may not always have a significant positive effect on shareholder value for every firm.
Figure 3(a) and Figure 3(b) show the posterior means of the SAT coefficient generated from the proposed models. We create a boxplot for each firm which contains its nine-year point estimates (posterior means). For the majority of the firms on average, as suggested by the positive posterior means, their customer satisfaction and shareholder value associations are positive. However, the estimates of association for each firm are very different. The boxplots for some of the firms have large spread, indicating that the difference between the largest estimate and the smallest estimate over the span of study years is quite substantial. This observation backups our previous statement that the association between customer satisfaction and shareholder value is time varying.
Figure 4(a) and Figure 4(b) show the boxplots of posterior means for each year under study, where each boxplot contains 70-firm point estimates. The spread of these boxplots is even larger than the ones in Figure 3(a) and Figure 3(b), which indicates that the SAT coefficients are substantively different from firm to firm. Since the magnitude of the link between customer satisfaction and shareholder value varies across firms, the importance of customer satisfaction may be treated differently by different firms.


Figure 2. (a) HBRM1’s posterior probabilities of the SAT coefficient to be positive for the 70 firms-arranged in an ascending order for each year; (b) HBRM2’s posterior probabilities of the SAT coefficient to be positive for the 70 firms-arranged in an ascending order for each year.
Table 3 presents the estimation results of proposed models, regarding the dynamic influences of industry and firm factors on the association between customer satisfaction and shareholder value. More specifically, Table 3 provides point estimates of the impact coefficients on the association as well as the posterior probabilities of the impact coefficients being positive. Note that the two models yield consistent results. Based on the results of HBRM2, market concentration (HHI) has a positive impact on the association over all 9 years from 1999 to 2007 and that the posterior probabilities of the coefficients being positive are above 0.9 for all the 9 years. That is, the association between customer satisfaction and shareholder value can be strengthened for firms in industries with higher market concentration consistently over time. In addition, the magnitude


Figure 3. (a) HBRM1’s boxplots of the 9-year SAT coefficient for each firm; (b) HBRM2’s boxplots of the 9-year SAT coefficient for each firm.
of the impact differs over time which indicates the dynamic influence of HHI on the association. Similarly, asset (AS) has a positive impact but advertising intensity (AD) has a negative impact on the association. However, there is not sufficient evidence in support of an impact of R&D intensity (RD) or demand growth (DG) on the association.
Finally, we compute log marginal likelihoods to compare the two Bayesian models. The values for HBRM1 and HBRM2 are −624.95 and −618.85 respectively. This result suggests that HBRM2 is preferred over HBRM1 for the data that are being investigated in the study.
6. Conclusions
In this paper we propose new Bayesian models to investigate the dynamic and heterogeneous link between customer satisfaction and shareholder value. Our results suggest that customer satisfaction does not have a homogeneous positive effect on the shareholder value for all firms. Instead, the magnitude of the link varies across firms and changes over time. The inter-firm difference is in general larger than intra-firm temporal difference. In addition, we find that the association


Figure 4. (a) HBRM1’s boxplots of the 70-firm SAT coefficient for each year; (b) HBRM2’s boxplots of the 70-firm SAT coefficient for each year.
Table 3. Bayes estimates of the impact coefficient of industry and firm factors on the relationship between customer satisfaction and shareholder value.
Note: Numbers in the two rows for each parameter in each year represent the posterior mean of the parameter and the corresponding posterior probability of the parameter being positive. Bold indicates probability is over 0.9 or below 0.1.
between customer satisfaction and shareholder value is consistently strengthened over time for larger firms and firms in industries with higher market concentration, but weakened for firms with high advertising intensity.
Methodologically, there are several advantageous features of the proposed models. First, our models provide individual level, time-varying estimates of the association. Without separating the part-worth into aggregate time dependent and static individual level components as in Liechty et al.’s model [17] , the proposed models are more general. Second, our models use industry and firm factors to help explain the variation on firm heterogeneity and time dependent part-worths. The impact of these factors is also allowed to be time varying in HBRM2, which means more flexibility in modeling. Third, by treating the joint posterior distribution of the parameter in the previous time period as the prior distribution of the parameters in the current time period, our proposed HBRM2 model requires prior specification at time t = 1 only without the need of introducing further subjective prior input afterwards.
Future work may include extensions of the method to handle different types of data such as panel choice data and extensions to include more complicated structure like an autoregressive structure in the model. It would also be desirable to obtain extensions that allow variable selection within the models.
Cite this paper
Fong, D.K.H., Chen, Q., Chen, Z. and Wang, R. (2017) An Application of Heterogeneous Bayesian Regression Models with Time Varying Coefficients to Explore the Relationship between Customer Satisfaction and Shareholder Value. Open Journal of Statistics, 7, 36-53. https://doi.org/10.4236/ojs.2017.71004
References
- 1. Fong, D.K., Ebbes, P. and DeSarbo, W.S. (2012) A Heterogeneous Bayesian Regression Model for Cross-Sectional Data Involving a Single Observation per Response Unit. Psychometrika, 77, 293-314. https://doi.org/10.1007/s11336-012-9252-x
- 2. Anderson, E.W., Fornell, C. and Lehmann, D.R. (1994) Customer Satisfaction, Market Share, and Profitability: Findings from Sweden. The Journal of Marketing, 58, 53-66. https://doi.org/10.2307/1252310
- 3. Fornell, C., Johnson, M.D., Anderson, E.W., Cha, J. and Bryant, B.E. (1996) The American Customer Satisfaction Index: Nature, Purpose, and Findings. The Journal of Marketing, 60, 7-18. https://doi.org/10.2307/1251898
- 4. Hallowell, R. (1996) The Relationships of Customer Satisfaction, Customer Loyalty, and Profitability: An Empirical Study. International Journal of Service Industry Management, 7, 27-42. https://doi.org/10.1108/09564239610129931
- 5. Ittner, C.D. and Larcker, D.F. (1998) Are Nonfinancial Measures Leading Indicators of Financial Performance? An Analysis of Customer Satisfaction. Journal of Accounting Research, 36, 1-35. https://doi.org/10.2307/2491304
- 6. Eklof, J.A., Hackl, P. and Westlund, A. (1999) On Measuring Interactions between Customer Satisfaction and Financial Results. Total Quality Management, 10, 514-522. https://doi.org/10.1080/0954412997479
- 7. Anderson, E.W. and Mittal, V. (2000) Strengthening the Satisfaction-Profit Chain. Journal of Service Research, 3, 107-120. https://doi.org/10.1177/109467050032001
- 8. Yeung, M.C. and Ennew, C.T. (2000) From Customer Satisfaction to Profitability. Journal of Strategic Marketing, 8, 313-326. https://doi.org/10.1080/09652540010003663
- 9. Gupta, S. and Zeithaml, V. (2006) Customer Metrics and Their Impact on Financial Performance. Marketing Science, 25, 718-739. https://doi.org/10.1287/mksc.1060.0221
- 10. Williams, P. and Naumann, E. (2011) Customer Satisfaction and Business Performance: A Firm-Level Analysis. Journal of Services Marketing, 25, 20-32. https://doi.org/10.1108/08876041111107032
- 11. Sun, K.A. and Kim, D.Y. (2013) Does Customer Satisfaction Increase Firm Performance? An Application of American Customer Satisfaction Index (ACSI). International Journal of Hospitality Management, 35, 68-77. https://doi.org/10.1016/j.ijhm.2013.05.008
- 12. Anderson, E.W., Fornell, C. and Mazvancheryl, S.K. (2004) Customer Satisfaction and Shareholder Value. Journal of Marketing, 68, 172-185. https://doi.org/10.1509/jmkg.68.4.172.42723
- 13. Gruca, T.S. and Rego, L.L. (2005) Customer Satisfaction, Cash Flow, and Shareholder Value. Journal of Marketing, 69, 1-130. https://doi.org/10.1509/jmkg.69.3.1.66358
- 14. Grewal, R., Chandrashekaran, M. and Citrin, A.V. (2010) Customer Satisfaction Heterogeneity and Shareholder Value. Journal of Marketing Research, 47, 612-626. https://doi.org/10.1509/jmkr.47.4.612
- 15. Allenby, G.M. and Ginter, J.L. (1995) Using Extremes to Design Products and Segment Markets. Journal of Marketing Research, 32, 392-403. https://doi.org/10.2307/3152175
- 16. Lenk, P.J., DeSarbo, W.S., Green, P.E. and Young, M.R. (1996) Hierarchical Bayes Conjoint Analysis: Recovery of Part Worth Heterogeneity from Reduced Experimental Designs. Marketing Science, 15, 173-191. https://doi.org/10.1287/mksc.15.2.173
- 17. Liechty, J.C., Fong, D.K. and De Sarbo, W.S. (2005) Dynamic Models Incorporating Individual Heterogeneity: Utility Evolution in Conjoint Analysis. Marketing Science, 24, 285-293. https://doi.org/10.1287/mksc.1040.0088
- 18. De Sarbo, W.S., Fong, D.K., Liechty, J. and Coupland, J.C. (2005) Evolutionary Preference/Utility Functions: A Dynamic Perspective. Psychometrika, 70, 179-202. https://doi.org/10.1007/s11336-002-0976-x
- 19. Aksoy, L., Cooil, B., Groening, C., Keiningham, T.L. and Yalcin, A. (2008) The Long-Term Stock Market Valuation of Customer Satisfaction. Journal of Marketing, 72, 105-122. https://doi.org/10.1509/jmkg.72.4.105
- 20. Morgan, N.A. and Rego, L.L. (2006) The Value of Different Customer Satisfaction and Loyalty Metrics in Predicting Business Performance. Marketing Science, 25, 426-439. https://doi.org/10.1287/mksc.1050.0180
- 21. Matzler, K., Hinterhuber, H.H., Daxer, C. and Huber, M. (2005) The Relationship between Customer Satisfaction and Shareholder Value. Total Quality Management & Business Excellence, 16, 671-680. https://doi.org/10.1080/14783360500077674
- 22. Tobin, J. (1969) A General Equilibrium Approach to Monetary Theory. Journal of Money, Credit and Banking, 1, 15-29. https://doi.org/10.2307/1991374
- 23. Chung, K.H. and Pruitt, S.W. (1994) A Simple Approximation of Tobin’s q. Financial Management, 23, 70-74. https://doi.org/10.2307/3665623
- 24. Harrison, J. and West, M. (1999) Bayesian Forecasting & Dynamic Models. Springer, New York.
- 25. Rossi, P.E., McCulloch, R.E. and Allenby, G.M. (1996) The Value of Purchase History Data in Target Marketing. Marketing Science, 15, 321-340. https://doi.org/10.1287/mksc.15.4.321
Appendices
Appendix A: Table of Measurements
Appendix B: Derivation of Full Conditional Distributions for the HBRM1 Model
・ For and :
(15)
This expression is proportional to a Normal density, , where
(16)
(17)
(18)
where is the Kronecker product. This expression is proportional to a normal density, where
(19)
(20)
・
(21)
(22)
(23)
This expression is proportional to a Wishart density, , where
(24)
(25)
・
(26)
(27)
(28)
This expression is proportional to a Gamma density,
, where
(29)
A random sample from the joint posterior distribution can be obtained by generating random deviates iteratively and recursively according to the above full conditional distributions. We have simulated 30,000 iterations, out of which the last 20,000 iterations are used for generating parameter estimates. Convergence was checked by starting the chain from multiple initial values and by an inspection of trace plots.
Appendix C: Derivation of Full Conditional Distributions for the HBRM2 Model
We first derive the prior density , , by computing the posterior density of the parameters from time t and then replacing , by , respectively, in the ex- pression. If we substitute Equation (10) into Equation (9), we will have:
(30)
where follows a normal distribution . Thus, the likelihood function of is given by a product of normal densities, . Since a posterior density is proportional to the product of the corresponding likelihood function and prior density, and is a product of the individual prior densities, we have:
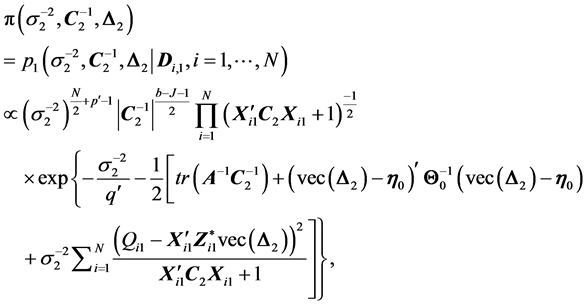 (31)
(31)
and in general, for ,
(32)
where and is the Kronecker product. Combining with the likelihood function, we obtain the following full conditional distributions:
・ For and :
(33)
(34)
This expression is proportional to a normal density, , where
(35)
(36)
・ For :
(37)
This expression is proportional to a normal density where
(38)
(39)
・ For :
(40)
This expression is proportional to a gamma density,
, where
・ For :
which is not a standard probability density except when t = 1. (In the case of t = 1, the above expression is proportional to a Wishart density.) Random deviates from the distribution can be generated using the Metropolis-Hastings algorithm with the following Wishart proposal density,
. Then, we will ac-
cept the proposed estimate with probability,
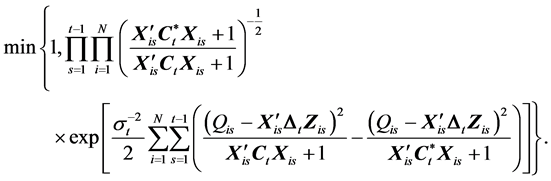 (43)
(43)
If the proposed estimate is not accepted, we will keep the current estimate of . A random sample from the joint posterior distribution can be obtained by generating random deviates iteratively and recursively according to the above full conditional distributions. We have simulated 40,000 iterations, out of which the last 20,000 iterations are used for generating parameter estimates. Convergence was checked by starting the chain from multiple initial values and by the inspection of trace plots.

Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
Or contact ojs@scirp.org
NOTES
1This relationship is illustrated as beta in the figure.



