Open Journal of Statistics
Vol.06 No.04(2016), Article ID:69627,11 pages
10.4236/ojs.2016.64050
Optimization of Expanded Polystyrene Lightweight Aggregate in Pre-Cast Concrete Blocks by a Completely Random Experimental Design (CRED) with Mixture and Process Variables
Raimundo Kennedy Vieira1, Raimundo Pereira de Vasconcelos1, Douglas Marangoni1, Adalena Kennedy Vieira2
1Nutec, Federal University of Amazonas (UFAM), Manaus (AM), Brazil
2Center Foundation of Analyses, Research and Technological―FUCAPI, Manaus (AM), Brazil

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 June 2016; accepted 7 August 2016; published 10 August 2016
ABSTRACT
The aim of this study was to determine the optimum design mix to produce pre-cast concrete blocks by a completely random experimental design (CRED) with mixture and process variables. The polymerized concrete was studied its composition: Cement, and water defined as the mixture compounds. To choose the best model, all the possible models were assessed through the ANOVA, which tested each possible model. The linear-linear model was preferred, since that do not pre- sent evidence of lack of fit, and it is capable of relating how to react the process variables, when are changed the variable mixture condition levels. The optimum experimental condition, obtained for the polymerized concrete, was: The size of the polystyrene beads was 4.8 mm sized polystyrene beads, 5.0% polystyrene that replaced the aggregate, 18.3% cement, 73.4% aggregate and 8.3% water. In this condition, the blocks made with polymerized concrete show a compressive strength above 15 Mpa, allowing its utilization in paving.
Keywords:
Experimental Design, CRED, Polymerized Concrete

1. Introduction
The use of raw materials in the civil construction industry has been very intense in recent years. This increase is very consistent in developing countries, which is motivated primarily by economic growth. It conveys many concerns, because the supply of types of raw materials used, is non-renewable resource. Although, the same economic growth expands the consumption of durable goods throughout their supply chain, it is also responsible for generating an amount of industrial waste.
The use of these residues, in partial or total substitution, of raw material in the civil construction industry, is a constant source of research [1] - [8] . It increases concerns, relating to the amount of solid residue from industry, which is overcrowding the landfill; more consistently to stimulate this kind of research. This investigation has stimulated the interest of researchers seeking new ways of using industrial waste as a solution for both shortage of natural resources for civil construction industry and the necessity of alternatives for the final destination of industrial waste. This type of application could allow the optimization of the natural resources without loss of quality of the final product.
In the major cities of the Amazon region, such as Manaus, this problem is much more critical due to its geological formation. It has rocks, which are easily accessible for use in construction, such as coarse aggregates to produce concrete blocks.
Alternatively, there is used gravel as coarse aggregates, which is obtained through dredging of riverbeds. The replacement of them with industrial waste, even minimally, already implies a direct improvement to the ecosystem of the region.
Also, the Industrial Pole of Manaus, where the electro-electronic companies are the principal industrial sector, generates much waste. This residue comes from packaging, which is based on expanded polystyrene, and does not have any final landfill destination.
In this context, this study presents an alternative technology for the use of waste polystyrene from packaging. This residue can be used as the aggregate in concrete for the production of blocks, after a burning process. These blocks could be used for construction walls or pavement. Thus, the purpose of this study was to obtain the most advantageous percentage and size of the polystyrenebeads that can be integrated to concrete as a substitute for aggregate, with minimum loss of compressive resistance with a CRED.
Vieira [9] used this methodology to determine the best percentage and size of the rubber tire that could be included to concrete for best performance. The first stage of this methodology is to define the experimental design to schedule how the variables will be studied.
The design of experiment employs multivariate optimization; this method has been applied more and more in many area of Engineering [10] [11] , Chemistry [12] and other fields. The gain of multivariate design lies upon a minimal experimental set-up cost; however, a set-up error is unlikely to be detected or identified. Other advantage, the interaction between the different factor can only be describe by application of multivariate techniques. When, it seeks to solve problems, independent of the study field, with experimental design, it should always take into account the type of variable under study. There are two great classes of variables:
Mixtures―in these variables, their properties not depend on their absolute magnitude, but the percentage of each constituent in the blend. The proportion of each constituent of the system has to be considered as a variable of mixture. These variables, which are dependent of others (i.e., when the quantity of one varies, the percentage of the others also varies). This definition could be better understood by a mathematical description [13] :
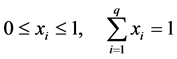 (1)
(1)
where, q is the number of constituent of the mixture and xi are the components.
Process variables―these are factors which can changes its levels without change the levels of others factors. For this reason they are independent and change without limitation [13] . Examples of models, which can be utilized to describe the behavior of process variables, are: [14] .
Linear: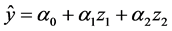 (2)
(2)
Bilinear: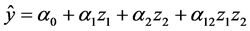 (3)
(3)
The models often applied to describe the effect of the mixture variables are: [14] ,
Linear: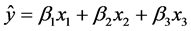 (4)
(4)
Quadratic: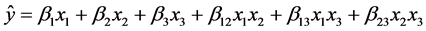 (5)
(5)
Special Cubic: (6)
(6)
where, a is the process model factor (the effects); b is the mixture model factor, z is the parameter of the process variable, x is the mixture variable parameter and 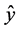 represents the value of the response calculated by the regression model.
represents the value of the response calculated by the regression model.
Nevertheless, these variables (process and mixture) can fit several systems where one or another has decisive influence. There are other types of systems where the response variable depends on both magnitude of the mixture constituents (mixture variables) and the effects of the process conditions [13] . In concrete system presented here, the response variables will be affected by any changes in the mixture variables (cement, aggregates, and water). Also by any variations in the level of process variables (the polystyrene beads aggregate size and proportion of replacement of polystyrene beads in concrete), as well as, by interaction between the two type of variables. In this situation, the utilization of a multivariate design which include the two type of variables (mixture and process) is great and advantageous. This advantage comes because it is possible to use models, which measure this kind of interaction. Such a model can be obtained by combining mixture models and process models. Thus, it is possible to obtain a combined modelby multiplying of two models: one of mixture and other of process variables. The Equation (7) presents acombined bilinear-linear model is generated by multiplying between the Equations (2) and (4), [14]
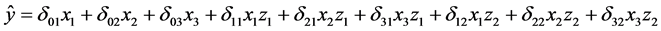 (7)
(7)
where, dij is the arrangement of ai and bj factors.
Situations where mixture and process variables are studied concomitant and its experiments are planned to be done in a completely random mode are encountered in the literature [9] [15] [16] . Although, there is a great number of problems with proposition of solution using a multivariate strategy presented in literature; however, are found just feel cases where the variables of process and mixture are simultaneous studied.
Due to the specificity of this type of design, they not involve necessary a great number of variables; however, the experimental set will require, generally, a large number of experiments, it will depend of the system size in study. In this case, it is recommended to do a preliminary study only with mixture or process variables to exclude the variables that are not influence in the system. The planning suggested is a factorial.
An alternative to this method will be the perform the experiment in blocks by application of a split-plot design, as used by several authors [17] - [22] . The split-plot design would facilitate the feasibly of experiments, but on the other hand, would become quite complex to define the parameter models errors, compared with procedure for a completely randomized design.
The aims of this study was to determine the optimum design mix to produce pre-cast concrete blocks by a completely random experimental design (CRED) with mixture and process variables. The use this procedure will generate a fast response without the need to use complex mathematical or statistic models.
This paper is organized as follows: In introduction (Section 1) are shown the motivation and justification, as well is initiating a short Literature Review about application of experimental design. This review is completed with the topic Analysis of variance (Section 2). Section 3 presents the methodology applied in the study. In Sections 4 are presented three subitems: In the first one, it relates there place effect of polystyreneasa substitute of aggregates in concrete; in the second one, it presents the results relate to mixture effect in concrete; and in the thirst one, it analyzes the effect of polystyrene. The last section presents the conclusions of the article.
2. Analysis of Variance
Analysis of variance depends of type model analyzed, for a factorial planning with two factors, for example: Z1 and Z2, with levels “f” and “g”, and “n” replicates. In this case,the variance model analysis will correspond to Equation (8), according Montgomery, [23] , but only if the experiments are carried out in a random form.
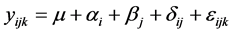 (8)
(8)
where:
 ;
;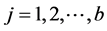 ;
;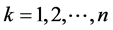 ; µ is the global average of all responses; ai represents the effects of i-thA factor treatment; βj the effects of j-thB factor treatment; (d)ij interactions effects between A and B and eijk represents a random error.
; µ is the global average of all responses; ai represents the effects of i-thA factor treatment; βj the effects of j-thB factor treatment; (d)ij interactions effects between A and B and eijk represents a random error.
Analysis of Variance, ANOVA, is the common way to verify the significance of model coefficients. The procedure standard of ANOVA is to evaluate the general observations’ variability in its components. The procedure consists to confirm the hypotheses tests by application of F tests. These tests are applied by relation of F factor tabled and calculated in the characteristic studied. The F factor calculated is obtained by relation between Square Means, corresponding to model characteristics, which would be tested. These Square Means are calculated by relation between square sums by degrees of freedom of characteristic studied. Finally, the square sum is determinate by variability credited for each factor. The sum of individual contributions will constitute the experimental error. The square sum is calculated by the observation deviation around of estimate media of studied characteristic. The ANOVA design with complete randomization of experiments is shown in Vieira et al. [9] .
The statistics model’s parameters are determinate by least squares method. It can be done through the matrix equation: (XtX)−1 (Xty), in which X represents the design matrix and the y, the observed responses variable. The estimative coefficients’ errors can be calculated by the equation (XtX)−1 s, where the s2 term represents the calculated experimental variance [24] .
3. Material and Method
In this topic is presented the materials utilized and the experimental design carried out, in this study.
3.1. Material
This study utilized one type of spherical EPS beads produced for a local industry (Manaus), which recycles its EPS after use. Due to the possibility of manufacturing beads with relative homogeneity, it was chosen from three interval diameter of beads: 1.2 mm to 2.4 mm; 2.4 mm to 4.8 mm and; larger than 4.8 mm (Figure 1). Table 1 shows the data relating to the aggregates and the EPS bead properties. The type of Portland cement used was CP II Z. This cement is produced in Manaus. The sand utilized in this study is from natural river sand.
Figure 1. Expanded polystyrene beads after burning process.
Table 1. Material properties and mix proportioning of control mixtures.
*As described in Table 2. Ä% of Polystyrene beads that substituted the aggregate.
Development of this research, only were analyzed fine and coarse aggregates that were treated as production variables and mixed with water and cement, constituting the mixture variables. Process variables were chosen, as were the EPS beads size and their percentage which substituted the aggregate in concrete.
3.2. Modeling
The experimental design applied in this study followed the Completely Random Experimental Design (CRED) with a mixture and process variables combined as presented by Vieira [9] .
In this study the set of mixture variables had three compounds: cement, aggregates and water. The process variables were definedas: Size of the polystyrenebeads and proportion of polystyrene beads which substitute aggregates. These two types of variables were simultaneously adjusted.
Table 2 presents the experimental design applied in this study. It was used as analytical responses compression strength (MPa) regarding 28-d for all the experimental conditions, shown as well in Table 3.
Table 2. A 32 factorial design with size EPS beads and proportion of EPS beads that substitute aggregates and mixture design and water proportions for the CRED.
a) standardized variables.
Table 3. Experimental 28-d compressive strength EPS concrete determinations for the duplicated 54 experiment complete random design for two processes and three mixture variables.
The analytical responses are given as compressive strength, in megapascals. a) Formulation number from Table 2. b) Replicate number.
For this experimental design different combined models were tested. These models were obtaine d by com- bination of process variable models [Equations (2) and (3)] with mixture variable models [Equations (4)-(6)]. An example of this procedure is presented in Equation (7).
Mechanical properties of polymerized concrete were investigated through the use of specimens of a cylindrical shape, with dimension of 15 cm in diameter andof 30 cm in height. All experiments were carried out using the leads presented in Table 2, but in a random order.
The polymerized concrete wereproduced fixing the water/cement ratio in 0.5. A proportion of the fine aggregate (sand) was replaced by polystyrene beads. Mass percentage of polystyrene beads used was 5%, 15% and 25%.
The polystyrene beads which were utilized not have and pretreatment were only washed with water.
The effect of surface treatment has to be motivationof a different study. In this study, the polymerized concrete could be produced with the optimized conditions of process variables and mixture compounds.
4. Results
Due to the degree freedom number, between the others combined models possible only two models were examined. These models were: the linear [Equation (2)] and bilinear [Equation (3)] process variable models combined with the linear mixture model [Equation (4)].The others combined models embodying the others mixture models [(Equations (5) and (6)], require bigger numbers of degree freedom, which the experimental design carried out, in this study, cannot provide.
Table 3 presents the results of ANOVA for the combination between the modelsof linear process variable and linear mixture (Combined model L-L). The result for the combined model embodying the linear process model and bilinear mixture model was unnoticed, because it presented worse values of regression, when compared to the simplest model. The combined model L-L presented no significant Lack of fit. Once, the Lack of fit is obtained by division between the means square/main-plot pure error and means square ratio (MSLOF/MSPE) of 8.60/5.75 = 1.50 is less than the 95% confidence F18, 27 tabled value of 2.00. It indicates that the variance results are explained only by the uncertainty of the experimental errors, it is not evidence which the model cannot fit the data at a confidence level of 95%.
Table 5 presents data for the L-L combined model: Coefficients, standard errors and t-test values. The standard errors were obtained by the data showed in Table 4.
There is no specific method to be applied in setting the t-test for combined model [16] . One way to obtain the critical t-values is by application of a normal probability graph in the t-tests values presented in Table 5. Figure 2, shows this plotting, where values of cutoff are between two lines, and the model combined L-L after this adjustment is shown in the Equation (9):

Figure 3 presents the graph of relation between experimental values and predicted values obtained from Equation (9). The variations in the graph keep up a correspondence to a root average square error of 20.48. The distribution of the points can considered random about the line. It confirms the no evidence of Lack of fit for the
Table 4. CRED ANOVA table for combined linear-linear model experimental.
Table 5. Parameters, estimated standard errors and t-test ratios for the linear-linear combined model.
Figure 2. Graph of the values predicted by Equation (9) against the experimental values. The line representing exact agreement is also shown expanded.
Figure 3. Normal probability graph of the t-test values in Table 5. The points between the two lines were discarded.
L-L combined model. Another graph, which relates the residuals versus the predicted values also presents a random behavior, this graph is not presented in this study.
By analyzing the Equation (9), it is possible to note, which the term with greater values is associated to x3, this result is initially unexpected, because plastic concrete follows the Abrams law [25] . These concretes utilize high consumption of water beyond the amount needed to cement hydration. In this case, the increases of water/cement ratio will provide a decrease of compressive strength. Its occurs because the amount of water consumed, in this study, is lower. For this reason, the behavior of this concrete it is contrary to that suggested by Abrams law. For this kind of concretes, the greater the amount of water used in the mixture, the bigger the concrete compressive strength. It is because the water used provides a better plasticity of the mixture, i.e., the water serves as a “lubricant”, reducing the internal friction between grains, thus making it easier to accommodate grains and minimizing the formation of voids [26] .
The significance of crossing terms xz indicates which the levels of the size and proportion of additional Polystyrene beads interact with mixture variables and affect surface response. By analysing of each set of mixture separately for the least-square fit of process variables data, it will resuts the following set of equations:



When, each value of set mixture is substituted by values of x1, x2, and x3 into Equation (9), the coefficients resultants are consistent that presented by the Equations (10)-(12).
In consequence of significance of xz crossing terms, it is expected, which each set of mixture condition or different level of process variable will impact the variable response. This fact is evidenced by different coefficients obtained from Equations (10)-(12). In the Figure 4, is possible to verify the results of the data application presented in Table 3, in the Equations (10)-(12).
4.1. Polystyrene Beads Percentage Effect Substituting Aggregates in Concrete
Through the analysis of the Figure 4, it can be verified,which the compressive strength is inversely proportional to the percentage of Polystyrene beads that replace the aggregates. This performance was expected because the difference between the chemical composition of Polystyrene beads and the conventional concrete. Their compounds are usually formed by mineral products, while the Polystyrene beads are composed of polymer organic origin. Furthermore, this behavior is already described in the literature [27] - [29] , where the greater the replacement of Polystyrene beads by aggregate, the lower will be concrete compression strength. Thus, considering this level of variable studied, the best % of Polystyrene in concrete is 5.0%, and the optimum mixture condition is 18.3% cement, 73.4% aggregate and 8.3% water. When, are considered all the set of mixtures, it was observed which it is possible to produce a polymerized concrete with compressive strength above 15 MPa for 28 days. It allows many possibilities for the use in this of civil construction where the use of non-structural concrete is recommended.
4.2. Mixture Composition Effect
By analyzing the mixture sets, it is possible to identify the optimal mixture composition: x1 = 0.183; x2 = 0.734; x3 = 0.083. Each mixture compositionis presented different water/cement ratio, however this mixture set presents the greatest relationship. Considering what was previously discussed, the amount of water available for the mixture showed the major influence and contributed significantly to the compressive strength of concrete. This fact was determinant to impose this set as being the best.
4.3. Effect Regarding the Polystyrene Size
Finalizing, when considering the particle size of polystyrene beads, all mixtures composition shows a tendency
Figure 4. Process response surfaces for variation of size and proportion of EPS beads for each set of mixture variable conditions. Figures 4(a)-(c) correspond to each set of mixture and (d) compressive strength against of EPS beads size, with two levels of % EPS highlighted.
directly proportional between the size of polystyrene beads and the concrete compressive strength. In consequence of this, and considering this studied level of limit imposed on the variable studied, the best size of beads is 4.8 mm. This observation is obvious when are compared the compressive strength results versus the size of Polystyrene beads. It can be done by observation in Figures 4(a)-(c), in addition to Figure 4(d). This last figure, it ratifies this finding, because it shows the influence of increase in beads’ size and compressive strength. It is also related to proportion of polystyrene added, as already correlated by the set of mixtures presented in the other three previous figures (Figures 4(a)-(c)). The results found in the literature utilized a different size of beads, which becomes difficult to do any comparison.
The substitution of only 5.0% of Polystyrene beads seems a value without importance. However, it presents as environmental advance, considering the great amounts waste Polystyrene produced annually such as packing and construction residue. The percentage of replacement develops into more significant by the possibility of utilization of this blocks as paving without the need for pretreatment or additives.
5. Conclusions
The optimization method presented adequate performance to simplify operational procedures that require many experiments.
The combined process-mixture variable model has not presented evidence of Lack of fit. It can explain the changes that occur with the isolated changes in each variable (processes and mixtures) as well as the interactions that each has on the other. Considering this level of variable studied, the optimum condition in the polymerized concrete is: 4.8 mm sized polystyrene beads, 5.0% polystyrene beads that substituted the aggregate, 18.3% cement, 73.4% aggregate and 8.3% water.
The results indicate that it is possible to produce a polymerized concrete with compressive strength above 15 MPa for 28 days. Thus, the goals of this works were achieved and the material obtained could be used as block for paving or in walls.
This level of strength was obtained without and surface treatment in beads used or addition of additives. It allows many possibilities for the use in this of civil construction where the use of non-structural concrete. For future works, it is recommended its analysis as an element for thermal and acoustic insulation.
Acknowledgements
R. K. V. thanks the CAPES and the program PROAP.
Cite this paper
Raimundo Kennedy Vieira,Raimundo Pereira de Vasconcelos,Douglas Marangoni,Adalena Kennedy Vieira, (2016) Optimization of Expanded Polystyrene Lightweight Aggregate in Pre-Cast Concrete Blocks by a Completely Random Experimental Design (CRED) with Mixture and Process Variables. Open Journal of Statistics,06,594-604. doi: 10.4236/ojs.2016.64050
References
- 1. Demirel, B. (2013) Optimization of the Composite Brick Composed of Expanded Polystyrene and Pumice Blocks. Construction and Building Materials, 40, 306-313.
http://dx.doi.org/10.1016/j.conbuildmat.2012.11.008 - 2. Poon, C.S. and Lam, C.S. (2008) The Effect of Aggregate-to-Cement Ratio and Types of Aggregates on the Properties of Pre-Cast Concrete Blocks. Cement & Concrete Composites, 30, 283-289.
http://dx.doi.org/10.1016/j.cemconcomp.2007.10.005 - 3. Poon, C.S., Kou, S.C. and Lam, L. (2002) Use of Recycled Aggregates in Molded Concrete Bricks and Blocks. Construction and Building Materials, 16, 281-289.
http://dx.doi.org/10.1016/S0950-0618(02)00019-3 - 4. Raut, S.P., Ralegaonkar, R.V. and Mandavgane, S.A. (2011) Development of Sustainable Construction Material Using Industrial and Agricultural Solid Waste: A Review of Waste-Create Bricks. Construction and Building Materials, 10, 4037-4042.
http://dx.doi.org/10.1016/j.conbuildmat.2011.04.038 - 5. Kinuthia, J.M. and Nidzam, R.M. (2011) Towards Zero Industrial Waste: Utilisation of Brick Dust Waste in Sustainable Construction. Waste Management, 31, 1867-1878.
http://dx.doi.org/10.1016/j.wasman.2011.03.020 - 6. Kushwaha, M., Akhtar, S. and Rajput, S. (2013) Development of the Self Compacting Concrete by Industrial Waste (Red Mud). Development, 3, 539-542.
- 7. Hassan, I.O., Ismail, M., Noruzman, A.H., Yusuf, T.O., Mehmannavaz, T. and Usman, J. (2013) Characterization of Some Key Industrial Waste Products for Sustainable Concrete Production. Advanced Materials Research, 690, 1091-1094.
http://dx.doi.org/10.4028/www.scientific.net/AMR.690-693.1091 - 8. Ribas, L.F., Cordeiro, G.C., Vieira, A.K. and Vieira, R.K. (2012) A Methodology for Collection of Residential Construction Residue in Manaus. Journal of Environmental Science and Engineering, 1, 1149-1163
- 9. Vieira, R.K., Soares, R.C., Pinheiro, S.C., Paiva, O.A., Eleutério, J.O. and Vasconcelos, R.P. (2010) Completely Random Experimental Design with Mixture and Process Variables for Optimization of Rubberized Concrete. Construction and Building Materials, 24, 1754-1760.
http://dx.doi.org/10.1016/j.conbuildmat.2010.02.013 - 10. Antony, J. (2014) Design of Experiments for Engineers and Scientists. 2nd Edition, Elsevier, London.
- 11. Hosseini, S.A., Niaei, A., Salari, D., Vieira, R.K., Sadigov, S. and Nabavi, S.R. (2013) Optimization and Statistical Modeling of Catalytic Oxidation of 2-Propanol over CuMnmC2−mO4 Nanospinels by Unreplicated Split Design Methodology. Journal of Industrial and Engineering Chemistry, 19, 166-171.
http://dx.doi.org/10.1016/j.jiec.2012.07.020 - 12. Piepel, G., Pasquini, B., Cooley, S., Heredia-Langner, A., Orlandini, S. and Furlanetto, S. (2012) Mixture-Process Variable Approach to Optimize a Microemulsion Electrokinetic Chromatography Method for the Quality Control of a Nutraceutical Based on Coenzyme Q10. Talanta, 97, 73-82.
http://dx.doi.org/10.1016/j.talanta.2012.03.064 - 13. Kowalski, S.M., Cornell, J.A. and Vining, G.G. (2002) Split-Plot Designs and Estimation Methods for Mixture Experiments with Process Variables. Technometrics, 44, 72-79.
http://dx.doi.org/10.1198/004017002753398344 - 14. Bortoloti, J.A., Bruns, R.E., de Andrade, J.C. and Vieira, R.K. (2004) Split-Plot Design Optimization for Trace Determination of Lead by Anodic Stripping Voltammetry in a Homogeneous Ternary Solvent System. Chemometrics and intelligent laboratory systems, 70, 113-121.
http://dx.doi.org/10.1016/j.chemolab.2003.09.004 - 15. Coetzer, R.L. and Haines, L.M. (2013) Optimal Designs for Multiple-Mixture by Process Variable Experiments. In: Ucinski, D., Atkinson, A.C. and Patan, M., Eds., mODa 10—Advances in Model-Oriented Design and Analysis, Springer International Publishing, Cham, 45-53.
http://dx.doi.org/10.1007/978-3-319-00218-7_6 - 16. Hosseini, S.A., Niaei, A., Salari, D. and Nabavi, S.R. (2014) Modeling and Optimization of Combustion Process of 2-Propanol over Perovskite-Type LaMnyCo1-yO3 Nanocatalysts by an Unreplicated Experimental Design with Mixture-Process Variables and Genetic Algorithm Methodology. Journal of the Taiwan Institute of Chemical Engineers, 45, 85-91.
http://dx.doi.org/10.1016/j.jtice.2013.04.010 - 17. Alexandrino, G.L. and Poppi, R.J. (2014) Study of the Homogeneity of Drug Loaded in Polymeric Films Using Near-Infrared Chemical Imaging and Split-Plot Design. Journal of Pharmaceutical Sciences, 103, 2356-2365.
http://dx.doi.org/10.1002/jps.24051 - 18. Hinkelmann, K. and Kempthorne, O. (2012) Design and Analysis of Experiments, Special Designs and Applications. Vol. 3, John Wiley & Sons, Hoboken.
http://dx.doi.org/10.1002/9781118147634 - 19. Shrivastava, A.K. (2013) Efficient Construction of Split-Plot Design Catalogs Using Graphs. IIE Transactions, 45, 1137-1152.
http://dx.doi.org/10.1080/0740817X.2012.723840 - 20. Fang, L. and Loughin, T.M. (2013) Analyzing Binomial Data in a Split-Plot Design: Classical Approach or Modern Techniques? Communications in Statistics-Simulation and Computation, 42, 727-740
http://dx.doi.org/10.1080/03610918.2011.650264 - 21. Kristensen, K. (2012) Incomplete Split-Plot Designs Based on α-Designs: A Compromise between Traditional Split-Plot Designs and Randomised Complete Block Design. Euphytica, 183, 401-413.
http://dx.doi.org/10.1007/s10681-010-0318-5 - 22. AmbroSy, K. and Mejza, I. (2011) Statistical Properties of Some Supplemented Split-Split-Plot Design. Colloquium Biometricum, 41, 65-174.
- 23. Montgomery, D.C. (2008) Design and Analysis of Experiments. 8th Edition, John Wiley & Sons, Hoboken.
- 24. Xu, Y., Jiang, L., Xu, J. and Li, Y. (2012) Mechanical Properties of Expanded Polystyrene Lightweight Aggregate Concrete and Brick. Construction and Building Materials, 27, 32-38.
http://dx.doi.org/10.1016/j.conbuildmat.2011.08.030 - 25. Saradhi Babu, D., Ganesh Babu, K. and Wee, T.H. (2005) Properties of Lightweight Expanded Polystyrene Aggregate Concretes Containing Fly Ash. Cement and Concrete Research, 35, 1218-1223.
http://dx.doi.org/10.1016/j.cemconres.2004.11.015 - 26. Chen, B. and Liu, J. (2007) Mechanical Properties of Polymer-Modified Concretes Containing Expanded Polystyrene Beads. Construction and Building Materials, 21, 7-11.
http://dx.doi.org/10.1016/j.conbuildmat.2005.08.001 - 27. Pirola, F.C. (2011) Contribuição para o estudo de concreto seco utilizadona fabricação de peças de concreto para pavimentação de 50 MPa. MSc Thesis, Universidade Federal de Santa Catarina, Florianópolis.
- 28. Abrams, D.A. (1919) Design of Concrete Mixtures. Vol. 1, Structural Materials Research Laboratory, Lewis Institute, Chicago.
- 29. Benício B.N., Scarminio I.S. and Bruns R.E. (1995) Planejamento e Otimização de experimentos. 2nd Edition, Editora da Unicamp, Campinas.









