Received 9 March 2016; accepted 23 April 2016; published 26 April 2016

ABSTRACT

We focus on the development of model selection criteria in linear mixed models. In particular, we propose the model selection criteria following the Mallows’ Conceptual Predictive Statistic (C_p) [1] [2] in linear mixed models. When correlation exists between the observations in data, the normal Gauss discrepancy in univariate case is not appropriate to measure the distance between the true model and a candidate model. Instead, we define a marginal Gauss discrepancy which takes the correlation into account in the mixed models. The model selection criterion, marginal C_p, called MC_p, serves as an asymptotically unbiased estimator of the expected marginal Gauss discrepancy. An improvement of MC_p, called IMC_p, is then derived and proved to be a more accurate estimator of the expected marginal Gauss discrepancy than MC_p. The performance of the proposed criteria is investigated in a simulation study. The simulation results show that in small samples, the proposed criteria outperform the Akaike Information Criteria (AIC) [3] [4] and Bayesian Information Criterion (BIC) [5] in selecting the correct model; in large samples, their performance is competitive. Further, the proposed criteria perform significantly better for highly correlated response data than for weakly correlated data.

Keywords:

Mixed Model Selection, Marginal C_p, Improved Marginal C_p, Marginal Gauss Discrepancy, Linear Mixed Model

1. Introduction

With the development in data science over the past decades, people become more aware of the complexity of data in real life. Univariate linear regression models with independent identically distributed (i.i.d.) Gaussian errors cannot achieve good fitness for some types of data, especially for the data with observations that are correlated. For instance, in longitudinal data, observations are usually recorded from the same individual over time. It is reasonable to assume that correlation exists among the observations from the same individual and linear mixed models are therefore appropriately utilized for modeling such data.

Since linear mixed models are extensively used, mixed model selection plays an important role in statistical literature. The aim of mixed model selection is to choose the most appropriate model from a candidate pool in the mixed model setting. To facilitate this task, a variety of model selection criteria are employed to implement the selection process.

In linear mixed models, a number of criteria have been developed to characterize model selection. The most widely used criteria are the information criteria such as the AIC [3] [4] and the BIC [5] . Sugiura [6] proposed a marginal AIC (mAIC) which involved the number of random effects parameters into the penalty term. Shang and Cavanagh [7] employed the bootstrap method to estimate the penalty term of mAIC for proposing two variants of AIC. For longitudinal data, a special case of linear mixed models, Azari, Li and Tsai [8] proposed a corrected Akaike Information Criterion (AICc). In the justification of AICc, the paper mainly handled the challenge initiated by the correlation matrix under certain conditions for the mixed models. Vaida and Blanchard [9] redefined the Akaike information based on the best linear unbiased predictor (BLUP) [10] - [12] for the random effects in the mixed models, and proposed a conditional AIC (cAIC). Dimova et al. [13] derived a series of variants of the Akaike Information Criterion in small samples for linear mixed models.

Another information criterion, BIC, can be considered as a Bayesian alternative to AIC. In linear mixed models, BIC is converted from marginal AIC by replacing the constant 2 in the penalty by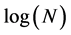, where N is the sample size (mBIC) [14] . Jones [15] proposed a measure of the effective sample size to replace the sample size in the penalty term of BIC, leading to a new criterion BIC_J.

We note that the BIC-type information criteria are derived using Bayesian approaches. Different from that, the AIC-type information selection criteria are justified from the frequentist perspective and based upon the information discrepancy. However, little research has relied on other discrepancy to propose criteria including Mallows’ C_p [1] [2] in linear mixed models. In fact, because of dissimilar derivation, each selection criterion has its own advantages, and no unique selection criterion can cover all the benefits for model selection. To further develop the selection criteria in the mixed modeling setting, we aim to justify the C_p-type ones relying on the Gauss discrepancy.

Mallows’ C_p [1] [2] in linear regression models targets to estimate the Gauss discrepancy between the true model and a candidate model. It serves as an asymptotically unbiased estimator of the expected Gauss discrepancy. Fujikoshi and Satoh [16] identified C_p in multivariate linear regression. Davies et al. [17] presented the estimation optimality of C_p in linear regression models. Cavanaugh et al. [18] provided an alternate version of C_p. The Gauss discrepancy is an L2 norm measuring the distance between the true model and a candidate model in linear models. To select the most appropriate model among competing fitted models, the candidate model leading to the smallest value of C_p is chosen. However, since the covariance matrix of linear mixed models poses the challenge for the justification of selection criteria, C_p statistic in linear mixed models has not been identified.

This paper extends the justification of C_p from linear models to linear mixed models. We first define a marginal Gauss discrepancy reflecting the correlation for measuring the distance between the true model and a candidate model. We utilize the assumption that under certain conditions, the estimator of the correlation matrix for the candidate model is consistent to that for the true correlation matrix. The marginal C_p, abbreviated as MC_p. MC_p serves as an asymptotically unbiased estimator of the expected marginal Gauss discrepancy between the true model and a candidate model. An improvement of MC_p, abbreviated as IMC_p, is also proposed and proved. We then justify IMC_p as an asymptotically more precisely unbiased estimator of the expected marginal Gauss discrepancy. We examine the performance of the proposed criteria in a simulation study where we utilize various correlation structures and different sample sizes.

The paper is organized as follows: Section 2 presents the notation and defines the marginal Gauss discrepancy in the setting of linear mixed models. In Section 3, we provide the derivations of the model selection criteria MC_p and IMC_p. Section 4 presents a simulation study to demonstrate the effectiveness of the proposed criteria. Section 5 concludes.

2. Marginal Gauss Discrepancy

In this section, we will introduce the true model, also called the generating model, and the candidate model in the setting of linear mixed models, then define the marginal Gauss discrepancy.

Suppose that the generating model for the data is given by

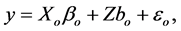(2.1)

where y denotes an N × 1 response vector, X_o is an N × p_o design matrix of full column rank, β_o is a p_o × 1 unknown vector for fixed effects. Z is an N × mr known matrix of full column rank and b_o is an mr × 1 unknown vector for random effects, where m is the number of cases, the sample size, and r is the dimension of the random effects for each case. Here, 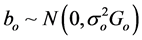, , 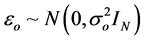and b_o and ε_o are mutually independent and G_o is a positive definite matrix and 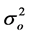is a scalar.

We fit the data with a candidate model of the form

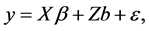(2.2)

where X is an N × p design matrix of full column rank, β is a p × 1 unknown vector, 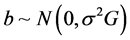, , 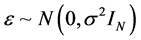and b and ε are mutually independent. The design matrix of the random effects Z and the random effects b are the same as those in the generating model. The matrix G is a positive definite matrix with the q unknown parameters in it.

Since the random part of the model (i.e. Zb) is not subject to selection, it is easier to use the marginal form in [19] of linear mixed models. Let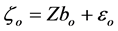, then the generating model (2.1) can be written as

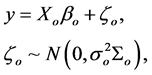(2.3)

where the scaled variance.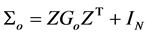

For the candidate model (2.2), let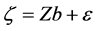, we have

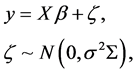(2.4)

where the scaled variance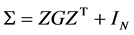. Therefore, the Σ is a nonsingular positive definite matrix.

In models (2.3) and (2.4), the terms ζ_o and ζ are the combinations of the random effects and errors in the model, respectively. Since they are both assumed to have mean zero, the parameters scaled variances Σ_o and Σ contain all the information of the random effects and errors, including the correlation structures.

We measure the distance between the true model and a candidate model by defining the marginal Gauss discrepancy based on the marginal forms of models (2.3) and (2.4). The true model is assumed to be included in the pool of candidate models. Let θ_o and θ denote the vectors of parameters and, respectively. The marginal Gauss discrepancy between the true model and a candidate model is defined as

where E_o denotes the expectation with respect to the true model. Note that the marginal Gauss discrepancy contains a weight of inverse scaled variance Σ⁻¹ into the L₂ norm. Therefore, the correlation between observations is involved when we use the marginal Gauss discrepancy to measure the distance between the true model and a candidate model.

Now let denote an estimate of θ. For instance, could be the maximum likelihood estimator (MLE) or the restricted maximum likelihood estimator (REML). However, in this paper, the MLE is utilized. The marginal Gauss discrepancy between the true model and the fitted candidate model is defined as

which can be therefore expressed as

(2.5)

We define a transformed marginal Gauss discrepancy between the true generating model and the fitted candidate model as a linear function of the marginal Gauss discrepancy (2.5) as

(2.6)

Taking the expectation of the transformed marginal Gauss discrepancy (2.6), we obtain the expected transformed marginal Gauss discrepancy as

(2.7)

To serve as a model selection criterion based on the expected transformed marginal Gauss discrepancy in Equation (2.7), an unbiased estimator or an asymptotically unbiased estimator will be proposed. To simplifying the procedure, we will first abbreviate this discrepancy in Equation (2.7).

From expression (2.7), the expectation part in the numerator can be written as

(2.8)

where is a projection matrix such that. To explore a further expression of (2.8), we need to know the properties of.

Theorem 1. For every, the matrix satisfies the following properties:

1) is idempotent.

2) and.

The proof is given in the Appendix.

Corollary 1. Following Theorem 1, we have:

1).

2).

3).

The proof of Corollary 1 can be easily completed following Theorem 1.

By Corollary 1, expression (2.8) can be written as

(2.9)

Note that the scaled variance Σ is a function of the q unknown parameter vector of variance components γ, i.e.,. Azari, Li and Tsai [8] noted that under the assumption that the set of candidate models includes the true model, it is reasonable to assume that the MLE is a consistent estimator of. Therefore, we can approximate by Σ, i.e.,. In what follows, we will make use of this approximation.

First, since and, using the approximation and Theorem 1, we have the first term of (2.9) as

(2.10)

Second, using the approximation again, the first term of Equation (2.7) can be simplified as

(2.11)

Using expressions (2.9), (2.10), and (2.11), in (2.7) can be therefore approximated as

(2.12)

Following Mallows’ interpretation, in (2.12) can be expressed as

where V_P and B_p are respectively “variance” and “bias” contributions given by

and

We comment that increasing the number of the parameters of the fixed effects p will decrease the bias B_p for the fitted model, yet will increase the variance V_P at the same time. The marginal Gauss discrepancy can therefore be considered as a bias-variance trade-off. Since a smaller value of the discrepancy indicates a smaller distance between the true model and a candidate model, the size of the Gauss discrepancy can really reflect how a fitted model is close to the true model.

3. Derivations of Marginal C_p and Improved Marginal C_p

3.1. Marginal C_p

In this section, model selection criteria based on are developed by finding a statistic that has an expectation which equals to or asymptotically equals to the expected transformed marginal Gauss discrepancy.

We start with the expectation of the sum of squared errors SS_Res from a candidate model. In linear mixed models, the sum of squared errors SS_Res can be written as

By Theorem 1 and Corollary 1, the expectation of the “scaled sum of squared error” can be expressed by

and then we have

(3.1)

Similar to the derivation of Equation (2.11), the numerator of first term of Equation (3.1) is expressed as

(3.2)

Then, by Equations (3.1) and (3.2), it is straightforward to construct a function, which is a linear combination of. It can be shown that the function T has the expectation

Note that the function T is not a statistic since the parameter is unknown. Here, we would like to use an estimator to replace in the function. Let denote the design matrix for the largest model in the candidate pool with. We assume that. Let represent the sum of squared errors for the corresponding fitted model and is written as

where and are the MLEs for parameters and in the largest candidate model respectively. The estimator cannot be expressed in a closed form and is calculated by computational algorithm where the iterations are needed.

For the estimator of, we use the mean squared error of the largest candidate model

(3.3)

which is an asymptotically unbiased estimator for, yet it is biased. In the justification of this estimator, using the approximation, we can represent in terms of, then the expected value of can be easily calculated as, i.e., asymptotically we can have. Serving as an asymptotically unbiased estimator of, the in Equation (3.3) for the largest candidate model is preferred to estimate.

MC_p is then obtained as

(3.4)

Note that MC_p is biased for. However, under the assumption that the true model is included in the pool of candidate models, MC_p serves as an asymptotically unbiased estimator of the discrepancy in expression (2.7). The proof is nontrivial, yet the simulations (not presented here) can show that as the samples size increases, the curves of the average values for MC_p and the discrepancy, along with IMC_p, which will be introduced in the following subsection, collectively get merged, indicating that MC_p and IMC_p are all asymptotically unbiased estimators of the discrepancy.

3.2. Improved Marginal C_p

To improve the performance of the MC_p statistic in linear mixed models, we wish to propose an improved marginal C_p, called IMC_p, which is expected to be a more accurate or less biased estimator of the expected transformed marginal Gauss discrepancy than MCp. IMC_p is proposed as

(3.5)

where SS_Res and are the sum of squared errors from the candidate fitted model and the largest fitted model, respectively. Note that IMC_p provides us an asymptotically unbiased estimator of, i.e., , and it will be shown in what follows.

To evaluate the expectation of IMC_p, we first need to calculate the ratio of the sum of squared errors between the candidate model and the largest candidate model in the pool. By Corollary 1, we have

By using the approximation for all, we approximate and by H and, respec-

tively, and and. Then, the ratio can be written as

(3.6)

To continue the proof, we will use the following theorem and corollary.

Theorem 2. If, then for any matrix K, we have.

The proof of Theorem 2 is presented in the Appendix.

Corollary 2. Following Theorem 2, we can obtain following results:

1).

2).

The proof of Corollary 2 is included in the Appendix.

By Theorem 1 and Corollary 2, we have

such that the quadratic forms and are independent. It follows that the

expectation of in (3.6) can be written as

(3.7)

For the term in (3.7), since, we have

(3.8)

For the term in (3.7), we can prove that

Note that. To justify the distribution of, we have

where. For the distribution of y, we know that. We calculate that, and by Theorem 1, the matrix is idempotent. Therefore, we have, where

and by Corollary 2, we can calculate λ as

Now, its inverse follows an inverse Chi-square distribution, i.e., , with the expectation as

(3.9)

Using the results of (3.8) and (3.9), we have the expectation of in (3.7) as

(3.10)

We recall that the criterion IMC_p in (3.5) is defined as

By the result of (3.10) and the approximation again , we have the expectation of IMC_p as

Hence, IMC_p is an asymptotically unbiased estimator of the expected overall transformed Gauss discrepancy in Equation (2.7). The advantage of IMC_p is that it avoids the bias of using to estimate to derive the criterion comparing to the derivation of MC_p.

We comment that the proposed MC_p and IMC_p are justified based upon the assumption that the true model is contained in the candidate models. Hence, we can calculate the MC_p and IMC_p values for the correctly and overfitted candidate models. However, the proposed criteria are also can be utilized for the underspecified models except that the values will be quite large and not behave well.

4. Simulation Study

In this simulation study, we investigate the ability of MC_p in (3.4) and IMC_p in (3.5) to determine the correct set of fixed effects for the simulated data in different models.

4.1. Presentation of Simulations

Consider a setting in which data are generated by the model of the following form

where the random effects are uncorrelated with mean 0 and variance, the errors are independent with each other with mean 0 and variance. It follows that the correlation between any two observa-

tions from the same case is, whereas the observations from different cases are uncorrelated. Let f denote the proportion between the variance of the random effects and the variance of the errors, i.e.. We can obtain that the correlation between the observations from the same case equals, which is an increas-

ing function of f. Therefore, a higher f implies a higher correlation between the observations in the same case.

For convenience, the generating model can also be expressed by

where are unknown coefficients of the fixed effects. It is assumed that the random effects with, and. We set for, an n_i-vector of ones, and . We also assume that the error term, and is independent of the random effects b.

Since the random part of the model (i.e. Zb) is not subject to selection, we would like to express the model by its marginal form. Let, we have

which can also be expressed by the general form as

(4.1)

where, is a scaled covariance matrix. Equivalently, the term has the following exchangeable correlation structure:, where, I is the identity matrix and J is the matrix of 1’s.

In this simulation study, we generate the design matrix X with of 5. The first column of X is 1 and the other four columns of X are generated randomly from uniform distributions but are fixed throughout the simulations. Therefore, the number of fixed effects including the intercept in the largest model is. We assume that the candidate vectors of covariates, from which the columns of X are to be selected, then there are candidate models in the candidate pool. Here, we will illustrate the behavior of model selection criteria by choosing three generating models:

1) Model 1:,;

2) Model 2:,;

3) Model 3:,.

These three models correspond to the three bs:, and in model (4.1) with the number of fixed effects equals 2, 3, 4, respectively. Again, the MLEs are used for estimation in the simulations.

Furthermore, we consider the case where the correlated errors have varying degrees of exchangeable structure. The variance component of error term is taken to be 1, and four values in an increasing order of are considered: 3, 6, 9, corresponding to three values of f: 3, 6, 9, respectively. We take the number of clusters (m) to be 5, 10 and 20, the number of repetitions in a cluster to be fixed at n = 5. We employ a total of 100 realizations for each model.

4.2. Results

4.2.1. Model 1:

Table 1 presents the performance of the two versions of marginal C_p (MC_p and IMC_p), mAIC and mBIC, under model 1 with the true fixed effects parameter, and corresponding to p_o = 2. The correct model selection rate for each criterion is listed. We observe that corresponding to each f, the IMC_p outperforms the MC_p, and both outperform mAIC and mBIC in selecting the correct model for small samples. With the increasing of the ratio f, we can observe the better performance in selecting the correct model from our proposed criteria.

4.2.2. Model 2:

We evaluate the proposed criteria for model 2 in the same manner as for model 1. Table 2 presents the performance of MC_p and IMC_p, mAIC and mBIC under model 2, where the true fixed effects parameter is and p_o = 3. The only change on model 2 from model 1 is that we add one more fixed effect variable X₅ and set the coefficient of that variable. In Table 2, the simulation results of model 2 are similar to those of model 1. With the increasing of the ratio f, we can have the better performance from our proposed criteria MCp and IMCp, indicating that the proposed MCp and IMCp can effectively fulfill the mission of model selection in the mixed models. We can also observe and conclude that IMC_p has improved the performance of MC_p for model selection in small samples. With the increasing of m, the performance of IMC_p and MC_p becomes closer. Comparing to the correct selection rates in model 1, all model selection criteria behave better in model 2.

4.2.3. Model 3:

As in the first two models, we evaluate the performance of model selection criteria by the rates in correctly selecting the true model. The results are presented in Table 3. Model 3 is identical to model 2 with the exception that we add one more significant fixed effect variable X₂ with the coefficient.

The simulation results of model 3 are similar to those of models 1 - 2. Considering the rates in choosing the correct model, we can find the trend of dramatic improvement of all criteria on model 3 over those on models 1 and 2, implying that the proposed MC_p and IMC_p essentially and effectively implement model selection when the fixed-effects are significant. In moderately large (m = 20) sample sizes, compared to that of mAIC and mBIC, MC_p and IMC_p have comparative performance in selecting the correct model.

5. Concluding Remarks

The simulation results illustrate that the proposed criteria MC_p and IMC_p outperform mAIC and mBIC when the observations are highly correlated in small samples. The results also show that with the increasing of the ratio f between the variance for the random effects and that for errors, the MC_p and IMC_p perform better. Since a larger f implies a higher correlation between the observations, we can conclude that with the correlation between observations increases, a better performance from the proposed criteria MC_p and IMC_p would be observed. Since the model with a small f which close to 0 is similar to a linear regression model with independent errors, our proposed criteria are not advantageous to be applied in such case.

The simulation results show that the proposed criteria MC_p and IMC_p significantly outperform mAIC and mBIC when the sample size is small. As the sample size increases, the performance of the proposed criteria becomes comparable to that of mAIC and mBIC. Therefore, MC_p and IMC_p are highly recommended in small samples in the setting of linear mixed models.

Our research (not shown in this paper) also shows that both proposed criteria behave best when the maximum likelihood estimation (MLE) is employed, comparing to those when the restricted maximum likelihood estimation or least squares estimation are used. The research on MC_p and IMC_p under REML estimation needs to be further developed in the future.

In the simulation study, by the comparison among models 1, 2 and 3, we see that when the true model includes more significant fixed effect covariates, the proposed criteria perform better in selecting the correct model. This fact indicates that the models with more significant variables (larger bs) are more identifiable by the proposed criteria than the models with variables which are not quite significant.

Comparing the performance between MC_p and IMC_p, we find that when the sample size is small, IMC_p obtains a higher correct selection rate than MC_p, which demonstrates that IMC_p improves the performance of MC_p in selecting the most appropriate model. However, when the sample size becomes larger, the performance of MC_p and IMC_p is quite identical.

Regarding the consistency of a model selection criterion, it means that as the sample size increases, the model selection will select the true model with probability 1. Note that MC_p, IMC_p, and mAIC are not consistent, whereas mBIC is consistent as expected since its penalty term prevents the overfitting in large samples. As the simulation study demonstrates, we can address again that the proposed criteria MC_p and IMC_p validate their advantages in small samples, although they are originally justified with large sample approximations, which is similar to quite a few other model selection criteria. The details for the consistency of model selection criteria in linear mixed models can also see Jiang and Rao [20] .

Cite this paper

Cheng Wenren,Junfeng Shang,Juming Pan, (2016) Marginal Conceptual Predictive Statistic for Mixed Model Selection. Open Journal of Statistics,06,239-253. doi: 10.4236/ojs.2016.62021

References

Appendix

Proof of Theorem 1. 1) To prove that is idempotent, we calculate

Thus, we prove that is idempotent.

2) By the properties of trace, we have

Therefore, we have

Thus, Theorem 1 is proved. □

Proof of Theorem 2. Let. We need to show that.

Since, there exists a p × 1 vector β₁ such that.

By, there also exists a p × 1 vector β₂ such that, which makes .

So we have. □

Proof of Corollary 2. 1) Since is positive definite, there exists an N × N matrix V with,

such that. It follows that.

Let, we can have. Then, we arrive at

Now, let

and

Since, by Theorem 2, we have, so that we can have, which leads to

The first part of Corollary 2 is therefore proved.

2) Following the first part proof of Corollary 2, since, we have. Then, we can conclude that

Therefore, the proof for the second part of Corollary 2 is completed. □

NOTES

^*Corresponding author.