Received 8 October 2015; accepted 14 December 2015; published 17 December 2015

ABSTRACT

The maximum of k numerical functions defined on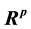, , by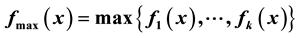, 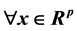is used here in Statistical classification. Previously, it has been used in Statistical Discrimination [1] and in Clustering [2] . We present first some theoretical results on this function, and then its application in classification using a computer program we have developed. This approach leads to clear decisions, even in cases where the extension to several classes of Fisher’s linear discriminant function fails to be effective.

Keywords:

Maximum, Discriminant Function, Pattern Classification, Normal Distribution, Bayes Error, L₁-Norm, Linear, Quadratic, Space Curves

1. Introduction

In our two previous articles [1] and [2] , it is shown that the maximum function can be used to introduce new approaches in Discrimination Analysis and in Clustering. The present article, which completes the series on the uses of that function, applies the same concept to develop a new approach in classification that can be shown to be versatile and quite efficient.

Classification is a topic encountered in several disciplines of applied science, such as Pattern Recognition (Duda, Hart and Stork [3] ), Applied Statistics (Johnson and Wichern [4] ), Image Processing (Gonzalez, Woods and Eddins [5] ). Although the terminologies can differ, the approaches are basically the same. In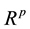, we are in the presence of training data sets to build discriminant functions that will enable us to do some classification of a future data set into one of the C classes considered. Several approaches are proposed in the literature. The Bayesian Decision Theory approach starts with the determination of normal (or non-normal) distributions 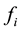governing these data sets, and also prior probabilities 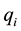(with sum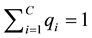) assigned to these distributions. More general considerations include the cost of misclassifications, but since in applications we rarely know the values of these costs they are frequently ignored. We will call this approach the common Bayesian one. Here, the comparison of the related posterior probabilities of these classes, also called “class conditional distribution functions”, is equivalent to compare the values of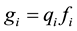, and a new data point 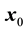will be classified into

the distribution 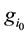with highest value of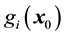, i.e..

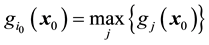On the other hand, Fisher’s solution to the classification problem is based on a different approach and remains an interesting and important method. Although the case of two classes is quite clear for the application of Fisher’s linear discriminant function, the argument and especially the computations, become much harder when we are in the presence of more than two classes.

At present, the multinormal model occupies, and rightly so, a position of choice in discriminant analysis, and various approaches using this model have led to the same results. We have, in,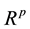

(1)

1) For discrimination and classification into one of the two classes, we have the two equations:

and their ratio, supposing the cost of misclassification can be ignored.

2) In general, using the logarithm of we have:

(2)

Expanding the quadratic form, we obtain:

,

where

and (3)

This function is called the quadratic discriminant function of class, by which we will assign a new observation to class when has the highest value among all. Ignoring, is called the linear discriminant function of class i. We will essentially use this result in our approach.

An equivalent approach considers the ratio of two of these functions

(4)

and leads to the decision of classifying a new observation as in class if this ratio is larger than 1.

The presentation of our article is as follows: in Section 2, we recall the classical discriminant function in the two-class case when training samples are used. Section 3 formalizes the notion of classification and recalls several important results presented in our two previous publications, which are useful to the present one. Section 4 presents the intersections of two normal surfaces and their projections on Oxy. Section 5 deals with classification into one of C classes, with. Fisher’s approach for multilinear classification is briefly presented there, together with some advantages of our approach. In Section 6, we present an example in classification with, solved with our software Hammax. The minimum function is studied in Section 7 while Section 8 presents the non-parametric approach, as well as the non-normal case, proving the versatility of Hammax.

2. Classification Rules Using Training Samples

Working with samples, since the values of are unknown, we use plug-in values of the means and variances and obtain the following results:

1) using and

The decision rule is then:

For a new vector, allocate it to class if

, (5)

and to class, otherwise. Here is the estimate of the common variance matrix, and can be obtained by pooling and.

We can see that the discriminant function is linear in, since

, (6)

where and if.

2) Different covariance matrices:

For a new vector, we consider the quadratic discriminate function, and allocate it to if

, (7)

and to, otherwise, where

3. Classification Functions

3.1. Decision Surfaces and Decision Regions

Let a population consist of C disjoint classes. We now present our approach and prove that for the two class case it coincides with the method in the previous section.

Definition 1. A decision surface is a surface defined in that separates points assigned to a specific class, from those assigned to other classes.

Definition 2. Let be a finite family of densities, with prior weights, with .

A max-classification function is a mapping from a domain into the discrete family, defined as follows:

For a value, , s.t..

3.2. Properties of g_max(×)

There are several other properties associated with the max function and we invite the reader to look at these two articles [2] and [1] , to find:

1) Clustering of densities using the width of successive clusters. -distance between 2 densities is well-known but does not apply when there are more than 2 densities. Let us consider k densities

with and let

.

A -distance between all densities taken at the same time, cannot really be defined, and the closest to it is a weighted sum of pairwise -distances. However, using, we can devise a measure which could be considered as generalized -distance between these k functions, since it is consistent with other considerations related to distances in general. This measure is

and is slightly different than the case. We have the double inequality

.

2) Considering now, we study the basic properties of, and its role as a classifier. Several original results related to -distances, overlapping coefficients and Bayes errors, are established, for two and more densities. This error can be shown to be and several applications were presented.

From [6] and [7] , we have the double inequality

with Bayes error given by

since still represents the unconditional probability of correct classification.

4. Discrimination between 2 Classes

For simplicity and for graphing purpose we will consider only the bivariate case in the rest of the article. However, all arguments can be applied to the case, and the basic answer on the classification of a new data point is still provided.

4.1. Determining the Function g_max

Our approach is to determine the function and use it with the max-classification function. This is

achieved by finding the regions of definition of in, i.e. by determining their boundaries as projections onto the horizontal plane of intersections between transformed normal surfaces, and the value of there.

1) For the two-class case we show that this approach is equivalent to the common Bayesian approach recalled earlier in Section 2. First, from Equation (6), equation determines precisely the linear boundary of the two adjacent regions where and respectively, and hence the two approaches are equivalent in this case. Second, from Equation (7), also determines the quadratic boundary (ies) of the region separating from since the two surfaces and intersect each other along curves which have quadratic projections (Straight lines, Ellipses, Parabolas or Hyperbolas) on the horizontal plane. But whereas the common Bayesian approach only retains only the linear, or quadratic, boundary for decision purpose, retains a partial surface on each side of the boundary and atop of the horizontal plane. This fact makes the max-classification function much more useful.

When the dimension of p exceeds 2 we have these projections as hyperquadrics, which are harder to visualize and represent graphically.

2) For the C classes case,: In general, when there are C classes the intersections between each of the couples of normal surfaces are space curves in, and their projections into the horizontal plane

determine definition regions of.

These regions are given below. Once they are determined they are clearly marked down as assigned to class i, or to class j, and the family of all these regions will give the classification regions for all observations. Naturally, definition regions for are deformations of those of, but have to be computed separately since there is no rules to go from one set of regions to the other. They are identical only in the case.

4.2. Intersections of Normal Surfaces

In the non-normal case, the intersection space curve(s), and its projection, can be quite complex (see example 6). Below are some examples for the normal case.

Two normal surfaces, representing and, always intersect each other along a curve, or two curves in, which, when projected in the (x, y)-plane, give(s) a quadratic curve, whose equation can be obtained by solving, where

.

In, taking the logarithm, we have:

Equaling the two expressions we obtain equations of the projections (in the horizontal plane) of the intersections curves in. There are several cases for these intersections, depending on the values of the mean vectors and the covariance matrices. We do not give them here, to avoid confusion, but they are sketched in the appendix and are available upon request. Instead, we give clear examples and graphs of the different cases.

1) A straight line (when covariance matrices are equal), or a pair of straight lines, parallel or intersecting each other.

2) A parabola: This happens when and and.

Example 1.

Let, , , and.

Figure 1 shows the graph of in 3D where the intersection of these two normal surfaces is a parabola.

’s boundary: The equation of this parabola is

3) An ellipse: When, and.

Example 2.

Let, , , , (and).

Figure 2 shows the graph of in 3D, where the intersection of these two normal surfaces is an ellipse.

The equation of this ellipse is

4) A hyperbola: This happens when and,.

Example 3. Let, , , , ,.

Figure 3 shows the graph of in 3D, where the intersection of these two normal surfaces is a

hyperbola.

The equation of this hyperbola is

5. Classification into One of C Classes (C ≥ 3)

The function is quite simple when the three class covariance matrices are equal, as can be seen from Figure 4(a). Then the discriminant functions are all straight lines intersecting at a common point. These lines are projections of normal surface intersection curves.

In the case these matrices are unequal they can intersect according to a complicated pattern, as shown in Figure 4(b).

5.1. Our Approach

For normal surfaces of different means and covariance matrices, in the common Bayesian approach we can use (6) or (7), or equivalently, classify a new value into the class such that. In the common Bayesian approach, we have the choice between:

1) One against all, using the discriminant functions (6), with the dichotomous decision each time: is in group j or not in group j.

2) Two at a time, using expressions (6) or (7) with regions delimited by straight lines or quadratic curves, each expression classifies new data as in or.

As pointed out by Fukunaga ([8] , p. 171) these methods can lead to regions not clearly assignable to any group.

In our approach, we use the second method and compile all results so that is now divided into disjoint sub-regions, each having a surface atop of it, which constitute the graph of in. Then, for a new observation, to classify it we just use the max-classification function given in Definition 2.

5.2. Fisher’s Approach

It is the method suggested first [9] , in the statistical literature for discrimination and then for classification. It is still a very useful method. The main idea is to find, and use, a space of lesser dimensions in which the data is projected, with their projections exhibiting more discrimination, and being easier to handle.

1) Case of 2 classes. It can be summarized as follows:

: Projection into a direction which gives the best discrimination: Decomposition of total variation

with and , We then search for a direction such that

is maximum, where and are projected values into that direction. We have with.

Fisher’s method in this case reduces to the common Baysian method if we suppose the populations normal. Implicitly it already supposes the variances equal. But Fisher’s method allows the consideration that variables can be can enter individually, so as to measure their relative influence, as in analysis of variance and regression.

2) Fisher’s multilinear method (extension of the above approach due to CR Rao): C classes, of dimension p and.

Projection into space of: Decomposition of total variation in original space:

, , , with

,

The projection from a p-dim space to a -dim space is done with a matrix and we have. Using, let the projected quantities be . We want to find the matrix so

that the ratio is maximum. Solving to obtain and then solving

to have eigenvectors, we obtain the matrix, which often is not unique. Within the -dim space a probability distribution can be found for the projected data, which will provide cut-off values to classify a new observation into one of the C classes.

We can see that Fisher’s multilinear method can be quite complicated.

5.3. Advantages of Our Approach

Our computer-based approach offers the following advantages:

1) It uses concepts at the base: Max of, and is self-explanatory in simple cases. It avoids several matrix transformations and projections of Fisher’s method, which could, or could not be done.

2) The determination of the maximum function is essentially machine-oriented, and can often save the analyst from performing complex matrix or analytic manipulations. This point is of particular interest when this analysis concerns vectors of high dimensions. To classify a new observation into the appropriate group, say, it suffices now to find the index so that. This operation can always be done since C is finite.

3) Complex cases arise when there are a large number of classes, or a large number of variables (high value for p). But as long as the normal surfaces can be determined the software Hammax can be used. In the case where p is much larger than the sample sizes, we have to find the most significant dimensions and use them only, before applying the software.

4) It offers a visual tool very useful to the analyst when. The full use of the function in necessitates the drawing of its graph, which could be a complex operation in the past, but not now. In general, the determination of the intersections between densities (or between) in, and their projections into, gives more insights into the problem: in classical statistical discriminant analysis, we only deal with these projections, and do not consider the curves in, of which they are projections (Equation (6) and Equation (7)). Hence, for any other family of densities which has the same intersections in as those already considered, we would have the same classification rule. For integration of is carried out using an appropriate approach (see [1] ) and classification of a new data point can again be made.

5) Regions not clearly assignable to any group, are removed with the use of, as already mentioned.

6) For the non-normal case, can still provide a simple practical approach to classification, as can be seen in Example 6, where does allow us to derive classification rules. [10] can be consulted for this case.

7) It permits the computation of the Bayes error, which can be used as a criterion in ordering different classification approaches. Naturally, the error computed by our software from data is an estimation of the theoretical, but unknown, Bayes error obtained from population distributions.

6. Output of Software Hammax in the Case of 4 Classes

The integrated computer software developed by our group is able to handle most of the computations, simulations and graphic features presented in this article. This software extends and generalizes some existing routines, for example the Matlab function Bayes Gauss ([5] , p. 493), which is based on the same decision principles.

Below are some of its outputs, first in the case of classification into a four-class population.

Example 4. Numerical and graphical results determining in the case of four classes in two dimensions, i.e., with

,

, where. Figure 5 gives the 3D graph of in Oxyz (with projections of the intersection curves onto Oxy):

To obtain Figure 6 we use all intersection curves given in Figure 7 below.

In this example we have all hyperbolas as boundaries in the horizontal plane. Their intersections will serve to determine the regions of definition of. Figure 8 below shows us these regions.

Classification: For the new observation, for example (25, 35), we can see that it is classified in.

Note: In the above graph, for computation purpose we only consider within a window in Oxy, with, , ,. We can show that outside this window the values of the integrals of are negligible and using these results we can compute.

7. Risk and the Minimum Function

1) When risk, as the penalty in misclassification, is considered in decision making we aim at the min risk rather than the max risk. In the literature, to simplify the process, we usually take the average risk, also called Bayes

risk, or the min of all max values of all different risks, according to the minimax principle.

We suppose here that risk has as its normal probability distribution, function of 2 variables x and y,

and various competing risks are present.

A minimum-classification function is defined similarly to.

Definition 4. A min-classification function is a mapping from a domain into the discrete family, defined as follows:

For a value, , s.t..

2) A relation between the max and min functions can be established by using the inclusion-exclusion principle:

Integrating this relation we have a relation between and various integrals on the minimums of subgroups of. For classification purpose we classify a new set of data as belonging to the

class having the lowest risk at that point. The function represents the minimum risk, but is, however, the invisible part of the graphs since it lies below all surfaces.

Example 5. The four normal distributions are the same as in Example 1 but represent the densities of the risks associated with the problem. Using the same prior probabilities the function is given by Figure 9(a) while its definition regions are given by Figure 9(b).

For, similarly to, we can approximately compute.

Remarks: a) For the two-population case this integral is also the overlap coefficient and can be used for inferences on the similarity, or difference between the two populations.

b) The boundaries between regions defining are in general linear or quadratic curves coming from the intersections of normal surfaces. Boundary between regions defining can be simpler since they might not come from these intersections.

8. Applications and Other Considerations

8.1. The Software Hammax

This software has been developed by our research group and is part of a more elaborate software to deal with discrimination, classification and cluster analysis, as well as with other applications related to the multinormal distribution. This software is in further development to be interactive and more user-friendly, and has its own

copyright. It will also have more connections with social sciences applications.

8.2. The Non-Parametric Density Estimation Approach

A more general approach would directly use data available in each group to estimate the density of its distribution. The function approach to classification would then follow, exactly as for the normal case. But, unless we approximate the density obtained by parametric methods, different regions of definition of can only be obtained empirically, to be used in the classification of a new data. Densities of all classes are now estimated by the classical kernel density estimation method for two variables, and. Using the kernel

,

they are estimated by

where is the j-th observation. Optimal values for and has been discussed by various authors ([11] ). We refer to [1] where a numerical example was redone, using density estimation. Also, we have the associated function. The Bayes error

,

computed by simulation, gives the same value as for the parametric normal case.

8.3. Non-Normal Model

As stated earlier an approach based on the maximum function is valid for non-normal populations. We construct here an example for such a case.

Let us consider the case where the population density in, given by

where, , are independent standard beta densities of the first kind, i.e.

,

with, and.

Similarly, we have:

where are also independent beta densities.

Example 6. For, , , , , and, and, the function is defined in by

We can see that the last two functions intersect each other along a curve in, the projection of which in is the discriminant curve giving the boundary between the two classification regions, as given by Figure 10, with an equation which is neither linear nor quadratic, since its expression is

where and. Figure 10 illustrates this case.

This curve will serve in the classification of a new observation in either of the two groups.

Any data above the curve, e.g. (0.2, 0.6), is classified as in Class 1. Otherwise, e.g. (0.2, 0.2), it is in Class 2. Numerical integration gives

9. Conclusion

The maximum function, as presented above, gives another tool to be used in Statistical Classification and Analysis, incorporating discriminant analysis and the computation of Bayes error. In the two-dimensional case, it also provides graphs for space curves and surfaces that are very informative. Furthermore, in higher dimensional spaces, it can be very convenient since it is machine oriented, and can free the analyst from complex analytic computations related to the discriminant function. The minimum function is also interested, has many applications of its own, and will be presented in a separate article.

Cite this paper

T.Pham-Gia,Nguyen D.Nhat,Nguyen V.Phong, (2015) Statistical Classification Using the Maximum Function. Open Journal of Statistics,05,665-679. doi: 10.4236/ojs.2015.57068

References