Open Journal of Statistics
Vol.05 No.01(2015), Article ID:53676,7 pages
10.4236/ojs.2015.51004
Separate-Type Estimators for Estimating Population Ratio in Post-Stratified Sampling Using Variable Transformation
Aloy Chijioke Onyeka, Chinyeaka Hostensia Izunobi, Iheanyi Sylvester Iwueze
Department of Statistics, Federal University of Technology, Owerri, Nigeria
Email: aloyonyeka@futo.edu.ng, chiyeaka2007@yahoo.com, isiwueze@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 January 2015; accepted 25 January 2015; published 30 January 2015
ABSTRACT
The study proposes, along the line of [1] , six separate-type estimators for estimating the population ratio of two variables in post-stratified sampling, using variable transformation. Properties of the proposed estimators were obtained up to first order approximations, both for achieved sample configurations (conditional argument) and over repeated samples of fixed size n (unconditional argument). Efficiency conditions, under which the proposed separate-type estimators would perform better than the associated customary separate-type estimators in terms of having smaller mean squared errors, were obtained. Furthermore, conditions under which some of the proposed separate-type estimators would perform better than other proposed separate-type estimators were also obtained. The optimum estimators among the proposed separate-type estimators were obtained and an empirical illustration confirmed the theoretical results.
Keywords:
Variable Transformation, Separate-Type Estimator, Optimum Estimators, Ratio, Product and Regression-Type Estimators, Mean Squared Error

1. Introduction
Information on auxiliary character has been used by many authors [2] - [9] in sample survey to improve estimates of population parameters of the study variable, and sometimes, information on several variables is used to estimate or predict a characteristic of interest, such as mean, total, ratio, and proportion. Reference [1] proposed the following six (6) estimators of the population ratio 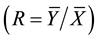 of the population means of two variables,
of the population means of two variables, 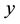 and
and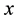 , under the simple random sampling scheme.
, under the simple random sampling scheme.
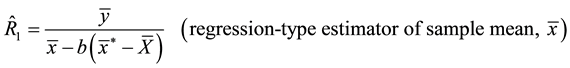 (1.1)
(1.1)
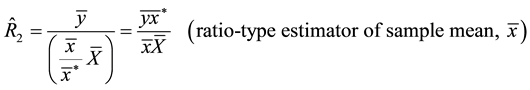 (1.2)
(1.2)
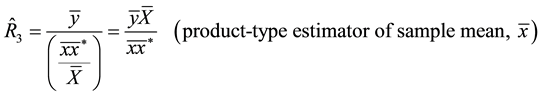 (1.3)
(1.3)
 (1.4)
(1.4)
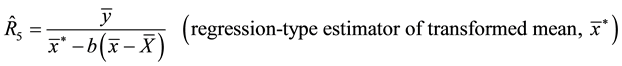 (1.5)
(1.5)
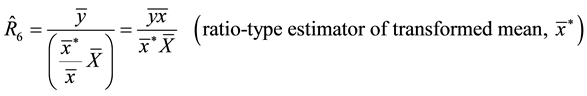 (1.6)
(1.6)
where,  ,
, 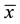 and
and 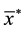 are sample means of the variables
are sample means of the variables ,
, 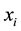 and
and 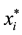 respectively,
respectively,
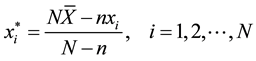 (1.7)
(1.7)

and b is a suitable constant, often chosen to be very close to the population regression coefficient of 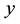
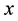
Reference [1] noted that authors like [8] [10] - [14] had used the variable transformation (1.7) or its equivalence in their respective studies. The obvious advantage of variable transformation is the introduction of an additional auxiliary (transformed) variable without additional cost, since the new auxiliary variable is a transformation of an already observed auxiliary variable. The work carried out by [1] was restricted to simple random sampling scheme. The present study extends the work carried out by [1] to post-stratified random sampling, by considering six (6) separate-type estimators of the population ratio of two variables in post-stratified random sampling, proposed along the line of the estimators proposed by [1] under the simple random sampling scheme.
2. The Proposed Separate-Type Estimators
Let 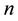
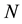

that

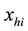
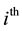
following variable transformation of the auxiliary variable, 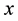
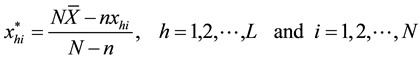
with the associated sample mean
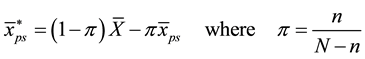
where 
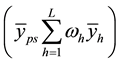
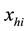

Using the sample means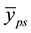
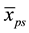
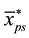
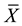


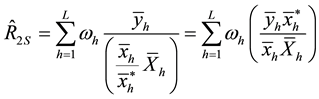
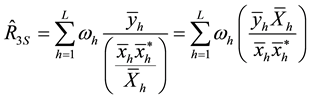
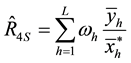
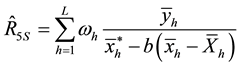
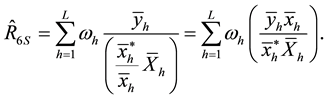
2.1. The Conditional Properties of the Proposed Separate-Type Estimators
Let

Then under the conditional argument,
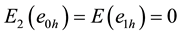
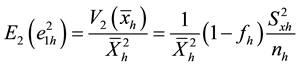
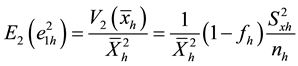
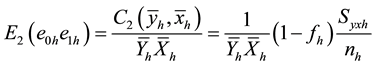
where 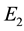
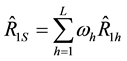
where
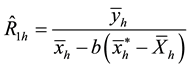
such that expanding up to first order approximation, 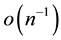
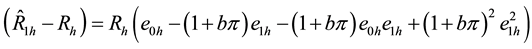
and
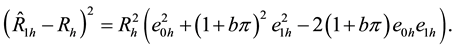
We take conditional expectation of (2.16) and (2.17) and use (2.10) to (2.13) to make the necessary substitutions to obtain the conditional bias and mean square error of 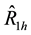
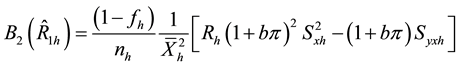
and
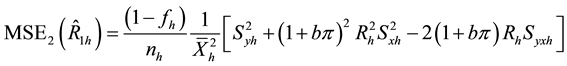
so that, using (2.14)
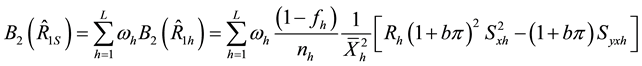
and
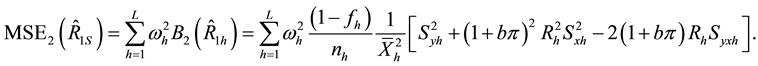
Following similar procedure, we obtain the conditional biases and mean square errors of the six proposed
separate-type estimators, together with those of the customary separate-type estimator, 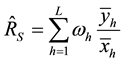
lation ratio 
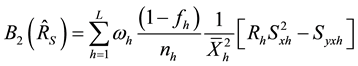
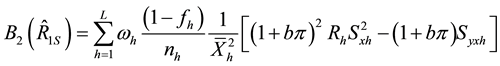
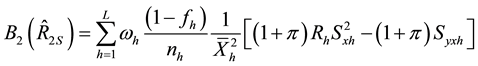
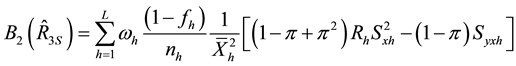
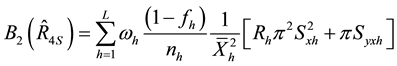
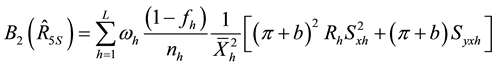
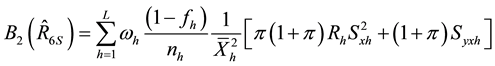
and,


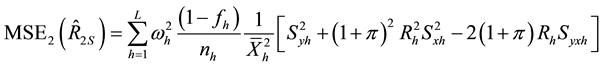
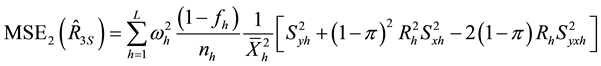
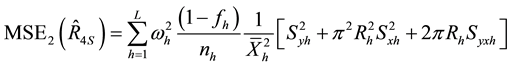
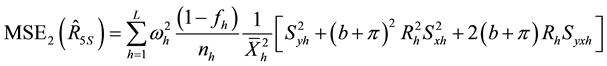
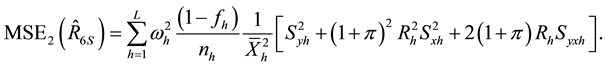
Generally, the conditional mean square errors of the proposed separate-type estimators are obtained as:
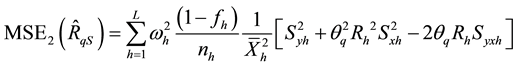
where 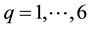
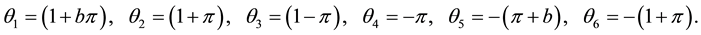
2.2. The Unconditional Properties of the Proposed Separate-Type Estimators
We take unconditional expectation of the conditional biases and mean square errors of (2.22) to (2.37) to obtain the unconditional properties of the separate type estimators as:
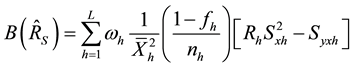
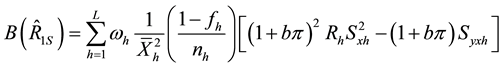
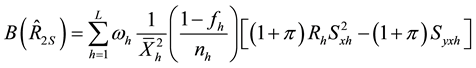
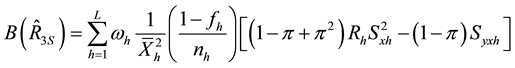
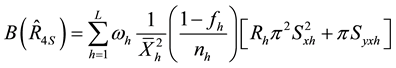
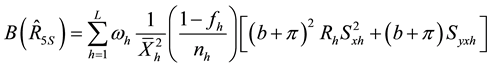
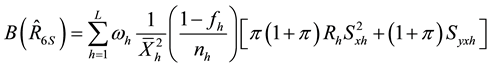
and,
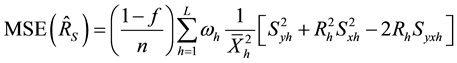
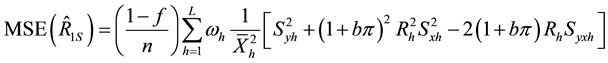
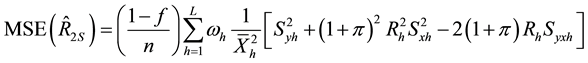
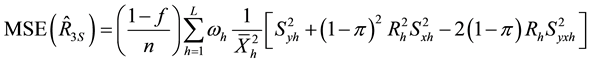
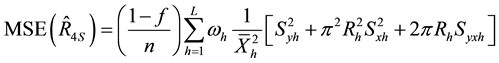


Generally, the unconditional mean square errors of the proposed separate-type estimators of the population ratio are obtained as:

3. Efficiency Comparison
The efficiencies of the six proposed separate-type estimators, 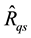
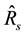
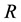
4. Numerical Illustration
Here, we use the final year GPA 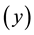
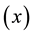
Table 1. Efficiency conditions under the conditional and unconditional arguments.
Where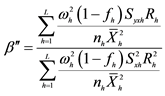
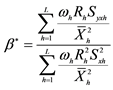
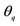
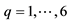
class consists of 50 students, with 32 and 18 students respectively falling into low-absenteeism (0 - 3 days per month) and high-absenteeism (4 - 6 days per month) groups or strata. Our interest is to estimate the ratio of final year GPA to absenteeism from lectures, based on a post-stratified sample of 20 out of the 50 students in the class. The data statistics, consisting mainly of population parameters, are shown in Table 2.
Table 3 shows the percentage relative efficiencies (PRE-1) of the proposed separate-type estimators, 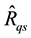
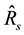

Table 3 shows that apart from the estimators, 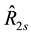
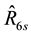
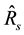


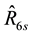
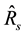
5. Concluding Remarks
The present study extended the use of variable transformation in estimating population ratio in simple random
Table 2. Data statistics for final year GPA (y) and absenteeism from lectures (x).
Table 3. Efficiency comparison of proposed separate-type estimators.
sampling scheme to post-stratified sampling scheme where we proposed six separate-type estimators. Efficiency conditions under which the proposed estimators performed better than the customary separate-type estimators were obtained. Both the theoretical and empirical comparisons show that the proposed estimators are not always better or more efficient than the customary separate-type estimator of the population ratio in post-stratified sampling. Consequently, in any given survey, these efficiency conditions should be employed to determine the appropriate separate-type estimators to use for estimating the population ratio of two variables in post-stratified sampling scheme using variable transformation. The major advantage of the proposed estimators is the use of additional (transformed) auxiliary variable without additional cost, since the additional auxiliary variable is a transformation of an already observed auxiliary variable.
References
- Onyeka, A.C., Nlebedim, V.U. and Izunobi, C.H. (2013) Estimation of Population Ratio in Simple Random Sampling Using Variable Transformation. Global Journal of Science Frontier Research, 13, 57-65.
- Cochran, W.G. (1940) The Estimation of the Yields of the Cereal Experiments by Sampling for the Ratio of Grain to Total Produce. The Journal of Agricultural Science, 30, 262-275. http://dx.doi.org/10.1017/S0021859600048012
- Robson, D.S. (1957) Application of Multivariate Polykays to the Theory of Unbiased Ratio-Type Estimation. Journal of the American Statistical Association, 52, 511-522. http://dx.doi.org/10.1080/01621459.1957.10501407
- Murthy, M.N. (1964) Product Method of Estimation. Sankhya, Series A, 26, 294-307.
- Singh, M.P. (1965) On the Estimation of Ratio and Product of the Population Parameters. Sankhya, Series B, 27, 321- 328.
- Sukhatme, P.V. and Sukhatme, B.V. (1970) Sampling Theory of Surveys with Applications. Iowa State University Press, Ames.
- Cochran, W.G. (1977) Sampling Techniques. 3rd Edition, John Wiley & Sons, New York.
- Onyeka, A.C. (2013) Dual to Ratio Estimators of Population Mean in Post-Stratified Sampling Using Known Value of Some Population Parameters. Global Journal of Science Frontier Research, 13, 13-23.
- Onyeka, A.C., Nlebedim, V.U. and Izunobi, C.H. (2014) A Class of Estimators for Population Ratio in Simple Random Sampling Using Variable Transformation. Open Journal of Statistics, 4, 284-291. http://dx.doi.org/10.4236/ojs.2014.44029
- Srivenkataramana, T. (1980) A Dual of Ratio Estimator in Sample Surveys. Biometrika, 67, 199-204. http://dx.doi.org/10.1093/biomet/67.1.199
- Upadhyaya, L.N., Singh, G.N. and Singh, H.P. (2000) Use of Transformed Auxiliary Variable in the Estimation of Population Ratio in Sample Survey. Statistics in Transition, 4, 1019-1027.
- Singh, H.P. and Tailor, R. (2005) Estimation of Finite Population Mean Using Known Correlation Coefficient between Auxiliary Characters. Statistica, Anno LXV, 4, 407-418.
- Tailor, R. and Sharma, B.K. (2009) A Modified Ratio-Cum-Product Estimator of Finite Population Mean Using Known Coefficient of Variation and Coefficient of Kurtosis. Statistics in Transition―New Series, 10, 15-24.
- Sharma, B. and Tailor, R. (2010) A New Ratio-Cum-Dual to Ratio Estimator of Finite Population Mean in Simple Random Sampling. Global Journal of Science Frontier Research, 10, 27-31.


