Open Journal of Statistics
Vol.05 No.02(2015), Article ID:55804,6 pages
10.4236/ojs.2015.52015
Analysis of Complex Correlated Interval-Censored HIV Data from Population Based Survey
Khangelani Zuma1,2, Goitseone Mafoko1
1Research Methodology and Data Centre, Human Sciences Research Council, Pretoria, South Africa
2Department of Statistics, University of South Africa, Pretoria, South Africa
Email: kzuma@hsrc.ac.za, gmafoko@hsrc.ac.za
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 December 2014; accepted 16 April 2015; published 20 April 2015
ABSTRACT
In studies of HIV, interval-censored data occur naturally. HIV infection time is not usually known exactly, only that it occurred before the survey, within some time interval or has not occurred at the time of the survey. Infections are often clustered within geographical areas such as enumerator areas (EAs) and thus inducing unobserved frailty. In this paper we consider an approach for estimating parameters when infection time is unknown and assumed correlated within an EA where dependency is modeled as frailties assuming a normal distribution for frailties and a Weibull distribution for baseline hazards. The data was from a household based population survey that used a multi-stage stratified sample design to randomly select 23,275 interviewed individuals from 10,584 households of whom 15,851 interviewed individuals were further tested for HIV (crude prevalence = 9.1%). A further test conducted among those that tested HIV positive found 181 (12.5%) recently infected. Results show high degree of heterogeneity in HIV distribution between EAs translating to a modest correlation of 0.198. Intervention strategies should target geographical areas that contribute disproportionately to the epidemic of HIV. Further research needs to identify such hot spot areas and understand what factors make these areas prone to HIV.
Keywords:
Interval-Censored, Weibul, Frailty, HIV, Survey

1. Introduction
Interval-censored data arise in research settings where the exact time an event occurs is not directly observed. In epidemiological studies that are cross-sectional in design, the time of the occurrence of an event is not observed but only an indication that it has either occurred or not. Knowing exact time of the occurrence of an event is crucial when interest is in estimating incidence of diseases such as HIV. HIV prevalence data is the most commonly available surveillance data. However, HIV incidence provides a more useful measure of epidemiological trends and sensitive indicator for evaluating impact of interventions. Incidence data are rarely available because their collection requires difficult, time-consuming and expensive follow-up of large cohorts. Thus, alternative laboratory based assays that can distinguish recent from long-term HIV infections from changes in antibody characteristics after seroconversion are becoming popular [1] . One such method is the BED capture enzyme immunoassay technique which can detect if HIV positive blood is infected within the last six months or longer [2] and thus leading to interval-censored data for those that are infected within the last six months, left censored data for those that are infected longer than six months and right censored data for those that are HIV negative at the time of the study. Estimation techniques for interval-censored data often stem from Cox proportional hazards model [3] . The model has been generalized to handle interval-censored data [4] .
In multi-stage cluster sampling, individuals belonging to the same cluster such as an EA share the same unobserved cluster-specific frailty effect and thus making them positively correlated. For example, in the HIV prevalence survey conducted in South Africa as described in Reference [5] , individuals from the same EA are considered to be more similar than those that are from different EA with respect to their observed risk behaviour, risk of HIV infection and other unobserved factors. These data are the subject of our analysis in Section 2. Frailties are considered mutually as independent random variables specified by some parametric distribution. Frailties are assumed independent given the parameters of their marginal distribution. The topic of frailty models has received considerable attention in demography [6] and statistics [7] in recent years. Gamma distribution for frailties, commonly assumed in frailty models, is conjugate to the right-censored data likelihood and thus simplifies computations. Several authors in both frequentist [8] [9] and the Bayesian viewpoints [10] - [12] have used gamma frailty.
The inclusion of frailty effects in the interval-censored data likelihoods proposed in references [4] [13] results in complex and intractable likelihood functions that often require numerical integration methods. The gamma frailty distribution is no longer conjugate. In the univariate context, the common fix-up approach is to assume that the event occurred at the beginning or end of each examination time and then use standard estimation techniques. However, this approach has been shown to lead to misleading results [14] [15] . The alternative approach is to ignore correlation in the data and utilize standard univariate techniques for interval-censored data [4] [13] . But, naive standard errors obtained through this approach can lead to invalid statistical inference [16] [17] . Other approaches that consider both infection time and frailties as unobserved random variables thus facilitating the use of expectation- maximization algorithm have been proposed [12] [18] .
In cross-sectional prevalence survey, the numbers of recently infected, and HIV negative can be used to estimate HIV incidence [19] . However, these estimation methods only provide point estimates of incidence with no functional forms for modeling the data and inclusion of key determinants of incidence. In this paper, we present an approach for joint modeling of left, right and interval-censored data when event times are correlated. The model is implemented using a population based household HIV prevalence survey that used BED techniques to classify infection as either recent or latent to estimate HIV incidence by different reporting domains [19] .
2. The Data
The data is from a household based population survey conducted in 2005 in South Africa. The design of the survey was based on a multistage stratified, clustered sampling scheme. The survey is conducted every after three years since 2002 to measure, partly, the impact of HIV. The survey targeted all persons that are 2 years old and above living in households. The survey excluded individuals living in educational institutions, old-age homes, hospitals and uniformed services barracks but included those living in hostels. The survey applied a multi-stage stratified sampling approach based on a master sample of 1 000 EA used by Statistics South Africa for the 2001 census. An EA consists of about 250 households. In this survey, 15 households were systematically selected within each EA. Three persons in each household were potentially eligible to be selected for the survey. And only one person was selected from each of the following age groups: 2 to 14 years old, 15 to 24 years old and 25 years old and above.
A total of 23,275 individuals aged 2 years old and older from 10,584 households were interviewed in the 2005 survey and 15,851 respondents agreed to be tested for HIV. Linked anonymous HIV testing was performed using dried blood spot (DBS) specimens. Socio-demographic and behavioural data were collected using a detailed questionnaire. Among those that were tested, 1449 tested HIV positive and among those that were HIV positive, 181 were diagnosed as recent infections using the BED [1] . This meant that 1268 (8%) were considered left censored, 14,402 (90.9%) right censored and 181 (1.1%) interval-censored. Point estimates of incidence from these data have been reported elsewhere [19] . The average number of people who were tested in an EA were 22 (standard deviation = 9.3). Covariates in our analysis include sex, race, age, locality type and marital status. Summary statistics for these variables are presented in Table 1.
3. Model and Parameter Estimation
The data to be analysed in this paper is clustered within an EA. Let 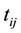
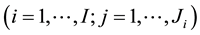 denote the event time for the jth individual in cluster i. Due to interval-censored nature of the data, the exact event time
denote the event time for the jth individual in cluster i. Due to interval-censored nature of the data, the exact event time  is unobserved. Instead, we only observe clinical endpoints
is unobserved. Instead, we only observe clinical endpoints 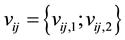 encompassing interval-censored event time
encompassing interval-censored event time 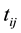 for those that are considered recently infected (infected within the last six months),
for those that are considered recently infected (infected within the last six months), 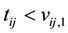 and
and 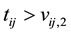 for those that are left and right censored respectively. Define censoring indicator
for those that are left and right censored respectively. Define censoring indicator 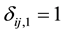 and
and 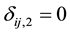 if left censored;
if left censored;  and
and 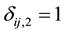 if interval-censored and
if interval-censored and 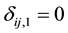 and
and 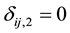 if right censored. This is similar to defining
if right censored. This is similar to defining 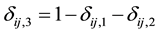 if right censored. The ith cluster specific frailty is denoted by
if right censored. The ith cluster specific frailty is denoted by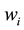 . The frailties are assumed to operate multiplicatively on the hazard function. Furthermore, Weibull baseline hazards
. The frailties are assumed to operate multiplicatively on the hazard function. Furthermore, Weibull baseline hazards 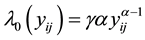 are assumed. The corresponding integrated baseline hazards are
are assumed. The corresponding integrated baseline hazards are
The model is framed as a shared frailty model defined as
where 
Table 1. Summary statistics for variables used in the hazard model.
frailty
where 
is 





where 
In this model, the density function for unobserved frailties is assumed to follow a Normal 

Maximum likelihood estimates are calculated using Newton-Raphson optimization for the corresponding (approximate) full data log-likelihood function.
A similar model with parameterization consistent with the accelerated failure time model formulation used in PROC LIFEREG in SAS has been used before [20] . Here, we have formulated the likelihood in the proportional hazards settings by adding a frailty term to the (linear) log-hazard component of the model. PROC NLMIXED in SAS can be used to find maximum likelihood estimates for this model. NLMIXED uses adaptive Gaussian quadrature to approximate the cluster-specific likelihood contribution. This is an attractive feature of this approach that it can be readily implemented using existing commercial statistical computing software.
4. Results
The methods of estimating point estimate of incidence described by [1] uses an adjustment formulae that corrects for both sensitivity and specificity specified by the BED analysis. Using this method, the incidence of HIV among persons aged 2 years old and older is estimated at 1.4% per 100 person-years [95% CI: 1.0 - 1.18] with 571,000 new HIV infections estimated for 2005 in South Africa as first reported in [19] . Incidence of HIV appears to vary by age, sex, race, geographical type of the area and by other socio-behavioural factors. Being female or aged between 15 to 24 years old or being an African is associated with high incidence of HIV. Those residing in informal settlements have the highest incidence of HIV compared with other residential areas. Similar results are observed for those that are never married.
Table 2 presents univariate and multivariate results of the model presented in Section 3. In univariate analysis nearly all of the covariates are statistically significant, and the estimated effects of the covariates are in close agreement with findings from previous research. The hazards of being infected with HIV is significantly lower for males than females [HR = 0.72, 95% CI: 0.64 - 0.81]. The hazards of HIV infection are [HR = 1.68, 95% CI: 1.34 - 2.11] times higher for youth aged 15 to 24 years old compared with those aged 2 to 14 years old and similar to those aged 25 years old and above [HR = 1.57, 95% CI: 1.22 - 2.01]. Africans are associated with significantly higher risk of HIV infection than any other race [HR = 7.43, 95% CI: 6.17 - 8.95]. Urban informal areas have the highest risk of HIV infection compared with other residential areas [HR = 2.38, 95% CI: 2.24 - 2.54], rural formal [HR = 1.56, 95% CI: 1.30 - 1.87] and rural informal [HR = 1.94, 95% CI: 1.71 - 2.20] in relation to urban formal. Being married or ever been married has a protective effect against being infected with HIV. Those who have never been married are [HR = 2.91, 95% CI: 2.57 - 3.30] times more likely to be infected with HIV compared to those who have ever been married or are cohabiting.
Table 2. Parameter estimates of univariate and multivariate analyses.
Table 2 further presents results from a multivariate frailty models. The model with frailty term contains the effects of other covariates not specifically included in the model, which are common to individuals from the same EA. For example, the clustering effects at an EA may result from common community norms, exposure to common underlying risk factors of HIV such as other sexually transmitted infections that are endemic in some geographical areas. The frailty parameter represents the EA effect. The parameter is interpreted as the variance of the random effects distribution. Large values of the variance indicate greater heterogeneity between EAs and stronger association within members from the same EA. The estimated variance of the EA is 0.4947 (SD = 0.0437), highly significant when compared to the one-sided Z-test with critical value of 1.645 at 5 per cent level of significance. The estimate of the variance implies moderate degree of correlation in the risk of HIV infection between members from the same EA even after controlling for observed covariate effects. The estimated correlation is 0.198. Standard errors are slightly magnified in the model with frailty indicating that the fixed effect parameters are now estimated more realistically, but with lower precision. Therefore, treating each individual response as independent gives false impression that there is more information in the data than there really is.
The hazard estimates for locality type are drastically reduced in the multivariate frailty model. The inclusion of EA random effect term accounts for unobserved proneness of individuals within specific EAs which is a locality type in its own right. Therefore, the magnitude of the effect of locality type is reduced in the model that includes EA effect. This is important especially for intervention programs as it indicates the need to focus interventions more in some locality types than others. The lack of striking differences between the model with and without frailty is reassuring since the effect of EA is rarely considered in studies of HIV incidence.
5. Conclusions
Analyses conducted in this paper provide an approach to a complex problem of correlated interval-censored data, where the event time is not observed precisely. The model demonstrates the possibility of multivariate analyses of HIV incident data and also includes frailty effect in this complex model. Inclusion of frailties in the analyses of correlated HIV infection risk at an EA level is of critical programatic value. Evaluation of the impact of HIV intervention programs and their planning relies heavily on incident data. The importance of clustering effect at an enumerator level demonstrates the importance of focusing interventions at key geographical areas. HIV in South Africa is at an epidemic level with considerable geographical variability in HIV distribution with some areas carrying much higher burden at local levels than others [21] . Even in high HIV prevalence areas, there is considerable evidence of localised epidemics [22] . Analyses of data that adjusts for clustering effect provides an opportunity to investigate factors and identify potential geographical areas that contribute disproportionately to the epidemic of HIV. Even after controlling for some important risk factors, the risk of HIV infection varies considerably across EA. The importance of EA frailty term indicates that some geographical areas are at increased risk of HIV infection compared with others. Control measures of HIV should extend further from high-risk individuals to high-risk areas.
In a study conducted at Africa center [23] the hazard of HIV seroconversion was approximately twice higher in people who were currently unmarried but had a partner than among people who were currently married. In our univariate analyses the hazard of HIV seroconversion was approximately three times higher in unmarried. However, in the multivariate model, marital status was excluded due to collinearity with age. Baseline hazard parameters indicated a higher risk of HIV infection at young ages that gradually subsided for older people.
In the estimation phase, Gaussian-Hermite quadratures are used to approximate intractable integrals [24] . The final results are based on six quadrature points. Brillinger and Preisler [25] reported that results did not change much for quadrature points greater than eight. Moreover, even five quadrature points have been considered sufficient [26] [27] . The inherent disadvantage of using large number of quadrature points is the need for strong assumption of normally distributed random effects. For example, ten quadrature points fit a symmetric distribution thus forcing the tails of random effects distribution to be normal.
In conclusion, the results provide further insight to the understanding of the epidemic of HIV. The models fitted are quite complex. However, the ability of fitting these complex models using the standard software is encouraging.
Acknowledgements
Authors acknowledge generous funding received from Nelson Mandela Foundation, Swiss Agency for Development and Cooperation, USA Centers for Disease Control and Prevention and the Human Sciences Research Council. We wish to thank our colleagues and collaborators who participate in the survey. Finally, we wish to sincerely thank all the people of South Africa who willingly open their doors and give researchers some of the most private information and agree to also provide specimen for HIV testing.
References
- McDougal, S.J., Pilcher, C.D., Parekh, B.S., Gershy-Damet, G., Branson, Bernard. M., Marsh, K., et al. (2005) Surveillance for HIV-1 Incidence Using Tests for Recent Infection in Resource-Constrained Countries. AIDS, 19, S25-S30. http://dx.doi.org/10.1097/01.aids.0000172874.90133.7a
- Kennedy, S. Dobbs, T., Parekh, B.S., Pau, C.-P., Byers, R., Green, T., et al. (2002) Quantitative Detection of Increasing HIV Type 1 Antibodies after Seroconversion: A Simple Assay for Detecting Recent HIV Infection and Estimating Incidence. AIDS Research and Human Retroviruses, 18, 295-307. http://dx.doi.org/10.1089/088922202753472874
- Cox, D.R. (1972) Regression models and Life Tables (with Discussion). Journal of the Royal Statistical Society. Series B, 34, 187-220.
- Finkelstein, D.M. (1986) A Proportional Hazards Model for Interval-Censored Failure Time Data. Biometrics, 42, 845- 854. http://dx.doi.org/10.2307/2530698
- Shisana, O., Rehle, T., Simbayi, L., Parker, W., Zuma, K., Bhana, A., et al. (2005) South African National HIV Prevalence, HIV Incidence, Behaviour and Communication Survey. Human Sciences Research Council Publishers, Cape Town.
- Vaupel, J.W., Manton, K.G. and Stallard, E. (1987) The Impact of Heterogeneity in Individual Frailty on the Dynamics of Mortality. Demography, 16, 439-454. http://dx.doi.org/10.2307/2061224
- Clayton, D.G. and Cuzick, J. (1985) Multivariate Generalisations of the Proportional Hazards Model (with Discussion). Journal of the Royal Statistical Society. Series A, 148, 82-117. http://dx.doi.org/10.2307/2981943
- Klein, J.P. (1992) Semiparametric Estimation of Random Effects Using the Cox Model Based on the EM Algorithm. Biometrics, 48, 795-806. http://dx.doi.org/10.2307/2532345
- Sastry, N. (1997) A Nested Frailty Model for Survival Data, with an Application to the Study of Child Survival in Northeast Brazil. Journal of the American Statistical Association, 92, 426-435. http://dx.doi.org/10.1080/01621459.1997.10473994
- Clayton, D.G. (1991) A Monte Carlo Method for Bayesian Inference in Frailty Models. Biometrics, 47, 467-485. http://dx.doi.org/10.2307/2532139
- Bolstad, W.M. and Manda, S.O. (2001) Investigating Child Mortality in Malawi Using Family and Community Random Effects: A Bayesian Analysis. Journal of the American Statistical Association, 96, 12-19. http://dx.doi.org/10.1198/016214501750332659
- Zuma, K. (2007) A Bayesian Analysis of Correlated Interval-Censored Data. Communications in Statistics-Theory and Methods, 36, 725-730. http://dx.doi.org/10.1080/03610920601033710
- Huang, J. and Wellner, J.A. (1997) Interval Censored Survival Data: A Review of Recent Progress. In: Lin, D.Y. and Fleming, T.R., Eds., Proceedings of the 1st Seattle Symposium in Biostatistics: Survival Analysis, Springer-Verlag, New York, 123-169. http://dx.doi.org/10.1007/978-1-4684-6316-3_8
- Rucker, G. and Messerer, D. (1988) Remission Duration: An Example of Interval-Censored Observations. Statistics in Medicine, 7, 1139-1145. http://dx.doi.org/10.1002/sim.4780071106
- Odell, P.M., Anderson, K.M. and D’Agostino, R.B. (1992) Maximum Likelihood Estimation for Interval-Censored Data Using a Weibull-Based Accelerated Failure Time Model. Biometrics, 48, 951-959. http://dx.doi.org/10.2307/2532360
- Guo, S.W. and Lin, D.Y. (1994) Regression Analysis of Multivariate Grouped Survival Data. Biometrics, 50, 632-639. http://dx.doi.org/10.2307/2532778
- Wei, L.J., Lin, D.Y. and Weissfeld, L. (1989) Regression Analysis of Multivariate Incomplete Failure Time Data by Modeling Marginal Distributions. Journal of the American Statistical Association, 84, 1065-1073. http://dx.doi.org/10.1080/01621459.1989.10478873
- Dempster, A.P., Laird, N.M. and Rubin, D.B. (1977) Maximum Likelihood from Incomplete Data via the EM Algorithm (with Discussion). Journal of the Royal Statistical Society. Series B, 39, 1-38.
- Rehle, T., Shisana, O., Pillay, V., Zuma, K., Puren, A. and Parker, W. (2007) National HIV Incidence Measures? New Insights into the South African Epidemic. South African Medical Journal, 97, 194-199.
- Bellamy, S.L., Li, Y., Ryan, L.M., Lipsitz, S., Canner, M.J. and Wright, R. (2004) Analysis of Clustered and Interval Censored Data from a Community-Based Study in Asthma. Statistics in Medicine, 23, 3607-3621. http://dx.doi.org/10.1002/sim.1918
- Fraser-Hurt, N., Zuma, K., Njuho, P., Hosegood, V., Gorgens, M., Chikwava, F., et al. (2011) The HIV Epidemic in South Africa: What Do We Know and How Has It Changed? SANAC, Pretoria.
- Tanser, F., Barnighausen, T., Cooke, G.S. and Newell, M. (2009) Localized Spatial Clustering of HIV Infections in a Widely Disseminated Rural South African Epidemic. International Journal of Epidemiology, 38, 1008-1016. http://dx.doi.org/10.1093/ije/dyp148
- Barnighausen, T., Tanser, T., Gqwede, Z., Mbizana, C., Herbst, K. and Newell, M. (2008) High HIV Incidence in a Community with High HIV Prevalence in Rural South Africa: Findings from a Prospective Population-Based Study. AIDS, 22, 139-144. http://dx.doi.org/10.1097/QAD.0b013e3282f2ef43
- Abramowitz, M. and Stegun, I. (1972) Handbook of Mathematical Functions. Dover Publications, New York.
- Brillinger, D.R. and Preisler, M.K. (1983) Maximum Likelihood Estimation in a Latent Variable Problem. In: Karlin, S., Ameya, T. and Goodman, L.A., Eds., Studies in Econometrics, Time Series and Multivariate Statistics, Academic Press, New York, 31-65. http://dx.doi.org/10.1016/B978-0-12-398750-1.50008-5
- Bock, R.D. and Aitkin, M. (1981) Marginal Maximum Likelihood Estimation of Item Parameters: Application of an EM Algorithm. Psychometrika, 46, 443-459. http://dx.doi.org/10.1007/BF02293801
- Anderson, D.A. and Aitkin, M. (1985) Variance Component Models with Binary Response: Interviewer Variability. Journal of the Royal Statistical Society. Series B, 47, 203-210.







