Open Journal of Statistics
Vol.04 No.09(2014), Article ID:50500,7 pages
10.4236/ojs.2014.49065
Estimating Equations for Estimation of Mcdonald Generalized Beta― Binomial Parameters
Nthiwa M. Janiffer*, Ali Islam, Orawo Luke
Department of Mathematics, Egerton University, Njoro, Kenya
Email: *janienthiwa@yahoo.com, asislam54@yahoo.com, orawo2000@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 August 2014; revised 9 September 2014; accepted 25 September 2014
ABSTRACT
There has been a considerable recent attention in modeling over dispersed binomial data occurring in toxicology, biology, clinical medicine, epidemiology and other similar fields using a class of Binomial mixture distribution such as Beta Binomial distribution (BB) and Kumaraswamy-Bi- nomial distribution (KB). A new three-parameter binomial mixture distribution namely, McDonald Generalized Beta Binomial (McGBB) distribution has been developed which is superior to KB and BB since studies have shown that it gives a better fit than the KB and BB distribution on both real life data set and on the extended simulation study in handling over dispersed binomial data. The dispersion parameter will be treated as nuisance in the analysis of proportions since our interest is in the parameters of McGBB distribution. In this paper, we consider estimation of parameters of this MCGBB model using Quasi-likelihood (QL) and Quadratic estimating functions (QEEs) with dispersion. By varying the coefficients of the QEE’s we obtain four sets of estimating equations which in turn yield four sets of estimates. We compare small sample relative efficiencies of the estimates based on QEEs and quasi-likelihood with the maximum likelihood estimates. The comparison is performed using real life data sets arising from alcohol consumption practices and simulated data. These comparisons show that estimates based on optimal QEEs and QL are highly efficient and are the best among all estimates investigated.
Keywords:
Maximum Likelihood, McDonald Generalized Beta Binomial, Simulation, Quadratic Estimating Equations, Quasi-Likelihood

1. Introduction
Estimating functions have for sometimes been a key concept and subject of inquiry in research and it is known to be the most general method of estimation. The basis of this method is a set of simultaneous equations involving both the data and the unknown model parameters. To obtain an estimator, the estimating function is equated to zero and then solve the resulting equation with respect to the parameter in order to obtain parameter estimate. Estimating equations are not quite intensive in computation unlike MLEs. Moreover, the MLE estimators are based on the assumption that the distribution is known, however an estimating equation is free of such assumptions. The usual procedure is to take a parametric model, such as, the McDonald Generalized beta-binomial model to allow over as well as under dispersion and obtain maximum likelihood estimates of the parameters McDonald Generalized Beta Binomial (McGBB) distribution is a three-parameter distribution which is superior to KB in handling over dispersed binomial data. This procedure may produce inefficient or biased estimates when the parametric model does not fit the data well. Alternatively, more robust estimates, such as moment estimates, quasi-likelihood estimates (Breslow, 1990 [1] ; Moore and Tsiatis, 1991 [2] ), extended quasi-likelihood estimates (Nelder and Pregibon, 1987 [3] ), the Gaussian likelihood estimates (Whittle, 1961 [4] ; Crowder, 1985 [5] ), estimates based on the pseudo-likelihood estimating equations of Davidian and Carrol (1987) [6] and estimates based on quadratic estimating functions of Crowder (1987) [7] and Godambe and Thompson (1989) [8] can be considered. In this paper we consider estimating the parameters of McDonald Generalized Beta Binomial by the quadratic estimating equations (QEE’s) of Crowder (1987) [7] and Godambe and Thompson (1989) [8] and compared the small sample efficiency and bias properties of these estimates with the maximum likelihood estimates. By varying the coefficients of the QEE’s we obtain four sets of estimating equations. We compare the small sample efficiency of the five sets of estimates obtained by the QEE’s and the quasi-likelihood estimates with the maximum likelihood estimates. We compare estimated relative efficiencies of the estimates for two sets of real life data arising from alcohol consumption practices and simulation study. Estimation of the parameters by the six methods is discussed in Section 3. In Section 4 we compare small sample relative efficiencies. This study shows that if interest is on the point parameters then the GL is the method of choice followed by QL.
2. McDonald Generalized Beta-Binomial Distribution of the First Kind
Let  be a random variable following McDonald’s Generalized Beta-Binomial Distribution of the first kind (McDonald, 1984 [9] ; McDonald and Xu, 1995 [10] ) with three parameters,
be a random variable following McDonald’s Generalized Beta-Binomial Distribution of the first kind (McDonald, 1984 [9] ; McDonald and Xu, 1995 [10] ) with three parameters, 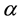 ,
, 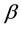 and
and . The probability density function of
. The probability density function of  is then given by
is then given by
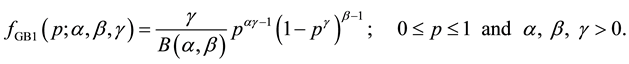 (1)
(1)
The 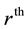 moment of the McDonald Generalized Beta-Binomial Distribution of the first kind is given by
moment of the McDonald Generalized Beta-Binomial Distribution of the first kind is given by
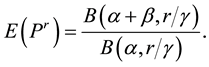 (2)
(2)
McDonald Generalized Beta Binomial Distribution
A random variable  is said to have McDonald Generated Beta Binomial (McGBB) Distribution with parameter
is said to have McDonald Generated Beta Binomial (McGBB) Distribution with parameter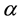 ,
,  and
and 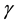 if and only if it satisfies the following stochastic representation.
if and only if it satisfies the following stochastic representation. 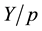 ~ Bin
~ Bin 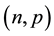
and 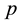 ~ GB1
~ GB1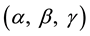 , where
, where




In general, a Binomial mixture is obtained through an integration approach. Suppose 





where 

3. Estimation of Parameters of McDonald Generalized Beta-Binomial Distribution
3.1. Maximum Likelihood Method
The three unknown parameters of McGBB distribution have been estimated using the maximum likelihood estimation technique. Let 

unknown parameter vector


3.2. Quasi-Likelihood
The quasi-likelihood (Wedderburn, 1974 [11] ) is based on the knowledge of the form of first two moments of the random variable





The quasi-likelihood with the above mean and variance is given by 
where,
By virtue of independence between samples, the quasi-likelihood with the above means and variance is given by:

We denote Equation (5) by



where, 

Then the partial derivatives for the three parameters






3.3. Quadratic Estimating Equations
By considering estimating functions quadratic in 



chastic functions of



The unbiased quadratic estimating equations for




If we take
We obtain the Gaussian estimating equations. We denote this Equation (10) by

If we take

Then we obtain the unbiased estimating equations (QEE’s) for McDonald Generalized Binomial Distribution. These equations were obtained by combining the quasi-likelihood estimating equations for the regression parameters and the optimal quadratic estimating equations of Crowder (1987) [7] for the dispersion parameter after setting 

We denote the estimates so obtained from Equation (11) by
This simplifies to,

For
We obtain the optimal quadratic estimating equations. We note that the forms of the skewness 

and
We denote the estimates obtained by solving these optimal quadratic estimating equations by 





4. Small-Sample Relative Efficiency
The asymptotic relative efficiency may not be very useful when comparing different estimators in small samples. So we conducted a simulation study using relatively small 













5. Estimation
Table 1 shows the data set used by Alanko and Lemmens (1996) [12] , Rodrίguez-Avi et al. (2007) [13] , and Chandrabose et al. (2013) [14] in the study of handling over dispersion. It shows the number of days an individual consumes alcohol y, out of n = 7 days in N = 399, where y = number of days, n = frequency of consumption. We used this data in Table 1 to obtain the estimates for 

6. Simulation
We compare the relative efficiency of the estimates 

Table 1. Number of alcohol consumption days and the frequency of consumption.
Table 2. The estimate 

Figure 1. Plot of relative efficiencies for various estimators relative to that of the MLE under McDonald Generalized Beta- Binomial model: for (a) relative efficiency comparison for 







using weekly (7 days) alcohol consumption survey data and simulated data for the survey of weekly alcohol consumption for a small time frame (





















7. Discussion
From Table 2, Table 3 and Table 4 we see that the methods QL, GL and 



Table 3. Relative efficiencies for various estimators for 


Table 4. Relative efficiencies for various estimators for 


8. Conclusion
The estimation functions are based on the knowledge of moments and one of the advantages of this approach is that it is robust to model misspecification. The comparison results in this paper indicate that the Estimating Equations are superior to MLE. The small relative efficiency for the estimates results also shows that estimates using optimal quadratic estimating functions of Crowder (1987) are highly efficient and are the best among all estimates investigated followed by Quasi-likelihood. Thus, we propose quadratic estimating function for estimation of point parameters of any model inclusive of McDonald Generalized Beta-Binomial instead of MLEs since they are consistent and robust to variance misspecification.
References
- Breslow, N.E. (1990) Tests of Hypothesis in Over-Dispersed Poisson Regression and Other Quasi-Likelihood Models. Journal of the American Statistical Association, 85, 565-571. http://dx.doi.org/10.1080/01621459.1990.10476236
- Moore, D.F. and Tsiatis, M. (1991) Robust Estimation of the Standard Error in Moment Methods for Extra Binomial/ Extra Poisson Variation. Biometrika, 47, 383-401. http://dx.doi.org/10.2307/2532133
- NeIder, J.A. and Pregibon, D. (1987) An Extended Quasi-Likelihood Function. Biometrika, 74, 221-232. http://dx.doi.org/10.1093/biomet/74.2.221
- Whittle, P. (1961) Gaussian Estimation in Stationary Time Series. Bulletin of the International Statistical Institute, 39, 1-26.
- Crowder, M.J. (1985) Gaussian Estimation for Correlated Binomial Data. Journal of the Royal Statistical Society, Series B, 47, 229-237.
- Davidian, M. and Carrol, R.J. (1987) Variance Function Estimation. Journal of the American Statistical Association, 82, 1079-1091. http://dx.doi.org/10.1080/01621459.1987.10478543
- Crowder, M.J. (1987) On Linear Quadratic Estimating Functions. Biometrika, 74, 591-597. http://dx.doi.org/10.1093/biomet/74.3.591
- Godambe, V.P. and Thompson, M.E. (1989) An Extension of Quasi-Likelihood Estimation. Journal of Statistical Planning and Inference, 22, 137-152. http://dx.doi.org/10.1016/0378-3758(89)90106-7
- McDonald, J.B. (1984) Some Generalized Functions for the Size Distribution of Income. Econometrica: Journal of the Econometric Society, 52, 647-663. http://dx.doi.org/10.2307/1913469
- McDonald, J.B. and Xu, Y.J. (1995) A Generalization of the Beta Distribution with Applications. Journal of Econometrics, 66, 133-152. http://dx.doi.org/10.1016/0304-4076(94)01612-4
- Wedderburn, R.M. (1974) Quasi-Likelihood Functions, Generalized Linear Models and the Gauss Newton Method. Biometrics, 61, 439-447.
- Alanko, T. and Lemmens, P.H. (1996) Response Effects in Consumption Surveys: An Application of the Betabinomial Model to Self-Reported Drinking Frequencies. Journal of Official Statistics, 12, 253-273.
- Rodríguez-Avi, J., Conde-Sánchez, A., Sáez-Castillo, A.J. and Olmo-Jiménez, M.J. (2007) A Generalization of the Beta-Binomial Distribution. Journal of the Royal Statistical Society, Series C (Applied Statistics), 56, 51-61. http://dx.doi.org/10.1111/j.1467-9876.2007.00564.x
- Chandrabose, M., Pushpa, W. and Roshan, D. (2013) The McDonald Generalized Beta-Binomial Distribution: A New Binomial Mixture Distribution and Simulation Based Comparison with Its Nested Distributions in Handling Over- dispersion. International Journal of Statistics and Probability, 2, 213-223.
NOTES
*Corresponding author.













