Received 25 May 2014; revised 28 June 2014; accepted 12 July 2014

ABSTRACT

This paper revises and expands the model Delta for estimating the knowledge level in multiple choice tests (MCT). This model was originally proposed by Martín and Luna in 1989 (British Journal of Mathematical and Statistical Psychology, 42: 251) considering conditional inference. Consequently, the aim of this paper is to obtain the unconditioned estimators by means of the maximum likelihood method. Besides considering some properties arising from the unconditional inference, some additional issues regarding this model are also going to be addressed, e.g. test-inversion confidence intervals and how to treat omitted answers. A free program that allows the calculations described in the document is available on the website http://www.ugr.es/local/bioest/Delta.

Keywords:

Model Delta, Multiple-Choice Tests, Agreement, Guessing

1. Introduction

Multiple-choice tests (MCT in the following) are widely known as psychometric instruments intended to measure the degree of knowledge of students about a specific matter. Nowadays, the enormous development in information technologies encourages new teaching methodologies in which MCTs constitute a fast and objective way of evaluation; especially when there is a large number of students. On the other hand, MCT also stimulate students’ active and self-managed learning. From a psychometric standpoint, MCTs are tools that can be adapted to different disciplines and knowledge levels, allowing high-level cognitive reasoning to be measured [1] . At the same time MCTs can give greater validity and reliability than other methods of [2] [3] . Nevertheless, how to determine the students’ degree of knowledge of the subject matter from responses to MCT is still a topic in debate [4] [5] .

In this paper we are going to consider a model to assess the students’ knowledge from MCT whose foundations were laid by Martín & Luna in 1989. We are going to call this model Delta. Originally the estimation of its parameters was addressed by means of a conditional method [6] . So the goal here is to develop the unconditional (maximum likelihood) procedure. Once we achieve this goal, we will review some of the features of the model based on the unconditional method and develop some additional advances; e.g. the estimation of the degree of knowledge in presence of unanswered questions, a usual situation that was not addressed in the original formulation. But before studying the unconditional method we will introduce the notation and give some background on the model Delta proposed by M & L.

The model Delta is applicable to MCTs of the type “single best-answer multiple-choice questions”. This type of test consists of 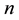items, each of which is composed of a statement (the stem) and alternative answers, of which only one is correct (the key) and the remainder are distractors [1] . When a student answers the items of an MCT, the raw data can be summarized as shown in Table 1. Here is the number of times that the alternative 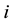is the correct answer, 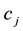is the number of times that the student gives the alternative answer 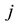and 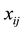refers to number of times that the student gives the alternative answer when the correct one is the alternative; obviously,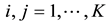. When there are omissions, 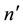stands for the number of items attempted and 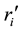for the number of answered questions when the alternative 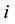is the correct one. In any case 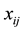and 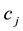refer to the number of answers given by the student and in presence of omissions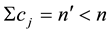. If matrix notation is needed, we will consider, , and for the components previously introduced.

In the past, various different scoring rules have been considered for evaluating a student’s degree of knowledge with respect to the data in Table 1. The simplest scoring rule that is consistent with number right scoring, has traditionally been criticized because it does not take random guessing into account, and this has given rise to various formula scoring rules [4] [7] - [9] . In 1982 Hutchinson [10] , using a model based on the theory of finite states, suggests that the test-taker’s knowledge level is given by a parameter which is estimated by the expression:

(1)

This rule, originally proposed by Lord and Novick [11] , is the classic penalty for guesses, according to which each incorrect answer is penalized with points. As Martín and Luna pointed out [6] , this implicitly assumes that the test-taker, when answering at random, chooses the alternative in question with a probability of, something that traditionally has been known as blind guessing or wild guessing [7] . However, these writers debate this uniform distribution of the guessing tendency. The idea is that the content of the distractors and their plausibility should give a pattern for the responses which is possible to be modelled.

The model proposed by M & L [6] follows Hutchinson’s concept, according to which the examinee is assumed to know a proportion of the subject-matter of the exam. However, they propose that in an MCT the average probability of choosing option j when is the correct one can be modelled by

, (2)

where is the Kronecker delta and the probabilities of the subject choosing the alternative in position when the answer is not known and is guessed (according to Lord and Novick,). Note that represents the probability of adequately choosing those questions where the correct option is the one occupying position, while in the opposite case, that is when, represents the probability of choosing a distractor. Obviously, the model requires that, , and.

According to this, the estimation of the examinee’s knowledge level proposed by M & L is:

, (3)

an expression which demonstrates that the relevant information for evaluating the test taker’s knowledge level is the sum of the proportions of successes, not the total of these. When the distribution of correct options in each position is homogeneous, that is if, then including when [6] ; this situation is of particular interest and we shall call it the balanced test.

Unlike the classical scoring rules, this model allows to address several questions of statistical inference: performing a contrast hypothesis on, determining a confidence interval (CI in the following) for, fixing the appropriate value of for various purposes, debating which is the appropriate value for, etc. [6] [12] . Furthermore, the extension of the model has allowed chance-corrected measures for evaluating the level of agreement (total or partial) between two raters to be defined [13] -[15] .

In their formulation, M & L [6] considered a conditional method to obtain the estimator. Nevertheless, it is possible to estimate by using an unconditional method, i.e. by using its estimator of maximum likelihood (from now on). The unconditional inference usually is less conservative than the conditional one, tests are more powerful and confidence intervals are narrower. Particularly this happens if the number of items is not high. The manner of obtaining this estimator and its implication in the inference problems mentioned is the aim of this paper.

2. Estimation of Parameters Using the Method of Maximum Likelihood

In the following and for the sake of simplification, let us focus on the particular case where the whole of the questions are answered. We will consider how to treat the more natural situation where there are omissions later on in this paper; but until then and.

Under M & L’s model, the rows, , of the frequency matrix in Table 1 are independent vectors which follow a multinomial distribution, where, whose parameters depend on the unknown parameters, because. A first consequence of the model, as the authors justify in Appendix I, is that the possible values for are limited to the set

, (4)

where. In addition, it can also be deduced from this model that the likelihood function will be given by a product of multinomial functions of probability. As the maximization of the function leads to a system of non-linear Equations with no explicit solution, M & L [6] proposed a conditional solution based on assuming that the values of and are previously fixed, i.e. and, which led them to the estimator. In Appendix II it is shown that the unconditional estimators of maximum likelihood for and respectively, are determined as follows:

A) When, the values of or of are not determined. In order to avoid this, one must increase all the data by 0.5―that is take the new data, and into account―and behave as in the following paragraphs.

B) When and, then and.

C) Otherwise is the only solution different to zero in the Equation:

, (5)

and the estimators are given by:

. (6)

Solutions in expression (5) must be looked for iteratively in the margins if and if, because when then and as noted in B.

Note that the model assumes that the values are not random variables (since they have been previously fixed by the examiner); when this is not the case, that is, when is a random vector of an unknown distribution, then by conditioning in the values obtained for the model described is obtained and all that has been stated above is valid.

In the particular case of ?as occurs with the tests with true/false type answers―then the solution to Equation (5) is:

(7)

where the third expression is the same value of expression (3) and the second is the Peirce criterion guessing parameter [16] (which refers to a simple difference between two proportions). In addition, through expression (6),

(8)

3. Fit of the Model

Given that and are estimators of maximum likelihood, and thus they have the well-known properties of this type of estimator, the fit of the model can be contrasted using the classic -test. The expected quantities will be given by, and the contrast statistic is the customary

, (9)

which will have to be compared in the classic manner with a theoretical distribution with degrees of freedom, since there are observed frequencies, parameters (and) are estimated and there are restrictions. The non-significance of the test means that the model fits well with the observed data.

One observation need to be made here about expression (9): when―as M&L showed [6] ―the model is saturated and, which means that the test makes no sense and the model is always valid.

4. Standard Error of the Estimators

In Appendix III the variance-covariance matrix of the estimators for the parameters of the model is obtained. The elements of greatest interest are and, to a lesser degree, , which are given (when) by:

, (10)

, (11)

where

(12)

By substituting parameters and in these expressions with their respective estimators and,

one finds that the estimate of standard error in these will be , respectively.

It can be seen that depends on itself and on the rest of the parameters of the model. The tendency is for to become smaller as, and increase.

Moreover, according to the exposition in Appendix III, the term inside the set of brackets in expression (10) corresponds to the exposition of a quadratic form depending on the parameters of the model which is positive-definite, so that the lower its value, the lower will be. Explicitly, this term is null if , that is, when are and. Let us note that while what we have just seen depends on the test-taker’s answer pattern and so is not controllable, the fact that the values are balanced is a question which the test maker decides in the design phase of the test and which, as will be seen in the following, can be very convenient as far as inference is concerned.

The fact that the values are balanced leads one to deduce that is in general lower than when these are not balanced. For the same values of, and, the values of the which are very disproportionate between each other can mean that in particular, is several orders of magnitude larger than when all of them are equal. In addition, for previously fixed values of and, in the balanced tests it is possible to characterize fully the behaviour of the maximum value of with respect to itself, something which cannot be done if. This possibility allows one to make predictions as to the number of items necessary for estimating the knowledge level of the examinee to a given precision. At the same time, the fact that the variance is generally lower, can be understood to mean that the balanced MCT are a preferable tool to those where the distribution of correct alternatives is not made homogeneously. In the following section we analyze the case of the balanced tests in greater detail, showing that the predictions carried out in these circumstances by M & L [6] [12] were a good fit, despite the fact that the estimator was not obtained under the principle of maximum likelihood.

5. Maximum Variance in MCTs with Homogeneous Distribution of the Correct Alternatives

5.1. General Case

If (for given values of and) maximum variability will be reached for, so that the maximum attainable variance is given by:

, (13)

an expression which coincides with the prediction of maximum variance carried out by M & L [12] for the balanced tests. This is why the consequences deriving from this expression (and which are set out in the following) are the same as the ones given by the said authors. The value of where the maximum is reached, let us say, depends only on the number of alternatives (it is independent of), and is given by

. (14)

It can be seen that the explicit value which takes is more sensitive to the lowest values of, but is always lower than 0.5, the level to which it approximates asymptotically when increases a good deal above what constitutes a multiple choice test. To illustrate, for values we have, respectively,; in order to arrive at it would be necessary to have alternatives! As a result, in the balanced tests, the maximum value of the variance only depends on and, and it does so according to expression

. (15)

From here on, one can estimate the effect that increasing the number of alternatives or the number of n questions has on the precision in estimating. Adding another option to each item implies a meaningful reduction in the variance down to or 5. For example, the maximum variance with alternatives is reduced by almost half (to be exact, by a factor of 0.562) when another alternative is added to obtain a test where. However, the maximum variance of the test where is only 1.266 times greater than that of a test where.

Similarly, adding more items to the test has a more meaningful effect in reducing the maximum variance when working with values lower than n.

An additional result is that one can determine the number of items in a test with alternatives which is equivalent, in terms of maximum variance, to another test with items and alternatives; the expression which links both sets of data is:

. (16)

For example, a test with items with alternatives has the same maximum variance, and thus can have the same precision for estimating, as one with items with alternatives.

Finally, in the tests with balanced values of it is possible to determine the value of maximum or (i.e. the “in the worst case” approach) necessary for reaching a given precision when estimating. Given the asymptotic normality of the estimator of maximum likelihood, and assuming that the estimation of can be the one with greater variance, the number of questions with alternatives for estimating with a precision of and a confidence, will be given by

. (17)

where is the percentile of a typical normal distribution. Similarly, the number of alternatives for estimating using questions with a precision of, will be:

. (18)

5.2. Special Case of K = 2

As has been pointed out previously, in the tests with only two alternatives (such as true/false) is precisely the solution of maximum likelihood. In this particular case, expression (9) is transformed into:

. (19)

However, the principle considered by M & L for obtaining this variance is still valid: if K = 2 the random variables are independent and are distributed as a binomial. Hence and

, (20)

a simpler expression than (19) and the estimation of which is given by

. (21)

The case of, represents a situation which allows a better appreciation of how the model functions. In this case the estimator originally proposed by Hutchinson [10] also coincides with the obtained by maximum likelihood, so that

(22)

Note that, for a given value of, the same estimation for is obtained if is constant, but the variance changes. Moreover, it is always possible to determine between which values this variance is found, in terms of; the maximum is obtained when (i.e.,), while the minimum occurs when or (i.e. one of the). The expressions for these bounds are:

(23)

6. Confidence Intervals for

6.1. General Case

The classic form of expressing the -confidence interval for is:

. (24)

In reality, in this situation a one-sided CI of the type is of more interest because it allows the student’s minimum degree of knowledge to be determined.

Agresti and Min [17] showed that for discrete data (like those shown here) it is more appropriate to obtain the CI by inverting a test because in that way narrower CI are obtained. In addition, it has the advantage of making the results of the test and the CI compatible. The principle is that if is the p-value associated with the test vs. -where - then the -CI associated with this is given

by. Because, where is the proportion of random answers

under the null hypothesis and the value of the expression (10) in and, then the CI is obtained by determining the two solutions and of the equality:

, (25)

where is the value of in. In Appendix II it is shown that in order to de-

termine the values of one should proceed as follows:

A) When, increase all the data by 0.5―that is consider the new data, and? and act as in the following paragraphs.

B) When, then.

C) When and then.

D) Otherwise,

. (26)

where is the only solution to the Equation:

, (27)

The solutions of expression (27) must be looked for iteratively in the margins max

when and when.

The problem with resolving expression (25) is that it is difficult to compute, because it is necessary to iterate it in and, in each iteration, the value must be obtained. If one wants a one-sided interval of the type then in expression (25) must be changed for.

6.2. The Case of K = 2

When then―as was indicated in expression (7)―and, that is, the parameter of interest is the difference between the two independent proportions, a parameter that appears a great deal in the literature and which is involved in the tests of equivalency of two proportions [18] . This has the advantage that the CI for may be obtained―both by exact and asymptotic methods―through the use of a great variety of both free and chargeable computer programs.

With regard to the chargeable computer programs, the most usual one is StatXact, a statistical software for small-sample categorical and nonparametric data problem solving [19] .

With respect to the free programs, the webpage http://www.ugr.es/local/bioest/ software gives a large number of these, both exact and asymptotic, and for the case in which the are previously fixed and for the case where they are not. In particular, the program Z_LINEAR_K.EXE (for the values, Beta1 = 1 and Beta2 = −1) allows the asymptotic CI for D to be obtained [20] .

A very simple (and reliable) procedure which allows one to obtain the asymptotic CI for is the one suggested by Agresti and Caffo [21] :

. (28)

where, with, and, that is, the classic Wald CI for the difference between two proportions but applied to the data increased by (when).

7. Treatment of Omitted Responses

Let us now consider how to treat omitted responses; i.e. when there is at least one such that, so that. In order to address this issue, we propose two alternative strategies: 1) the proportional correction of the degree of knowledge, or 2) the imputation of the omitted answers.

The first proposal consists in considering that the omissions are due to the fact that the student does not know the corresponding answers. Consequently, the idea is to estimate the degree of knowledge regarding the answered portion of the test and then correct this outcome by means of the total number of items according to

.

Thus a student who answers 50 out of 100 questions and gets with her/his attempts will have (25% of the subject) as the final outcome of the test. This proportional correction is also applied to the limits of the confidence intervals.

The second proposal is to consider the imputation of the omitted answers. Assuming the pattern given by the estimates, the idea now is to estimate from the transformed data given by

.

In this case, the confidence intervals are those obtained from this new data matrix.

When the MCT is balanced both methods give similar results. Otherwise, the imputation method implies a penalty for omissions that can be lower or higher depending on the pattern of the vectors of probabilities and omissions.

8. Examples

In Table 2 there are three examples of MCT with alternatives where the model is always suitable according to the test in section 3 (all the levels of significance are higher than 30%). Table 2(a) contains the data

which were considered in M & L’s original paper [6] . This is a balanced test and the results show that the original conditional estimation fitted well with respect to the maximum likelihood estimation; note that this includes the estimation of the variance. The confidence intervals obtained by classical methods and by inverting the test are also similar, although the second is more exact. The data in Table 2(b) are those for an unbalanced test. Greater discrepancy can now be seen between the results given by the maximum likelihood methods and the conditional method; the second one overestimates the student’s knowledge level compared to the former, and in addition, the estimation error in the conditional case is three times that of the unconditional one. Finally, in Table 2(c) the case in which is shown. Now the estimations and the inferences about can be carried out after increasing the data by +0.5.

Table 3 covers two cases of MCT with alternatives and thus the conditional and the unconditional methods coincide. If the estimation errors for are compared to those obtained in Table 2, it can be seen that by reducing in one alternative the result is an increase of this error. In Table 3(a) the discrepancy between the intervals obtained by the classic Wald method and those obtained by inverting the test can be seen. Finally in Table 3(b) the inferences and estimations are performed with the data increased by +0.5.

Table 4 shows the treatment of omitted answers according to the methods introduced in the previous section.

9. Discussion

In this paper the model Delta for MCT has been revised and expanded. This model allows for addressing the assessment of the level of knowledge of a MCT taker from a statistical perspective. Besides, it also allows objectively characterizing some properties of this kind of tests, such as the optimal number of choices or the test length.

Given that the estimator proposed by M & L was not obtained by using the principle of maximum likelihood, the aim of this paper has been to address this goal. Estimators derived by this method have some desirable properties; it is widely-known in statistics that they are consistent and asymptotically unbiased, efficient and normally distributed.

Regarding the main point on MCTs, the decision-taking as to whether or not the examinee exceeds a given knowledge level, according to Altman et al. [22] we have considered the standpoint of the confidence interval for instead of the contrast. In addition to the CI based on the asymptotic normality, the method recommended by Agresti and Min [17] has also been examined, because it should offer better results when the number of items is not very high.

Given that the proposed inference methods in this paper require a large amount of computation, readers may obtain a free program which carries these out, on the website of our group [23] .

The behaviour of Delta can be observed by means of simulations. Figure 1 shows the point estimation of the parameter across the entire range of knowledge in the case of MCT with three alternatives where each individual test is generated by the inverse transformation method. These simulations can be performed by the reader by using the program MCTsim, freely available on the previously cited Web site. All the details about the simulation method can also be found in the documentation of the program. Additionally, Table 5 shows the invariance of and its SE under all possible re-arrangements (permutations) of the distracters.

Let us conclude by saying that the model Delta is constructed from formal and consistent standpoints [12] . It generalizes measures for evaluating knowledge which have already been considered from the classic point of view by measurement specialists [4] [7] [11] . Furthermore, this model has been extended successfully to cover more complex situations [13] -[15] .

Acknowledgements

This research was supported by the Spanish Ministry of Education and Science, grant number MTM2012-35591 (co-financed by the European Regional Development Fund).

Cite this paper

PedroFemia-Marzo,AntonioMartín-Andrés, (2014) Multiple Choice Tests: Inferences Based on Estimators of Maximum Likelihood. Open Journal of Statistics,04,466-483. doi: 10.4236/ojs.2014.46045

References

Appendix I. Possible Values of

Since, then and. Hence

where and? because decreases with π_i and

increases with π_i. Because, so, then

, where the last statement is due to the fact that reaches its maximum value in. Hence expression (4).

Appendix II. Estimation of the Parameters of the Model

The likelihood function for the model under consideration is, where is the same as in expres-

sion (2). Hence, if:

. (A1)

This means that in order to obtain the estimators and for the parameters and, respectively, it is necessary to solve the Equations and.

1. Estimation of the Parameters π_i

Since, then and, therefore. This means that

, where is a constant to be determined, so that

, (A2)

where because all the terms that define it are larger than or equal to zero. If this expression is multiplied by there are two possibilities. If is added, one obtains:

. (A3)

If is worked out, one obtains:

, (A4)

The sum of which results in

. (A5)

By adding by in expression (A2) and substituting expression (A5) one obtains:

(A6)

From the above expressions it is possible to deduce some conditions to be verified by the constant. Thus, from (A3) it can be deduced that, from (A6) that if (and the reverse if) and, finally, because the value of expression (A3) is smaller than or equal to that of (A5), then si (and the reverse is true if). Therefore:

(A7)

In addition, from expression (A4):

. (A8)

In order to estimate the parameters one need only substitute with in expression (A4), which produces the following second degree Equation in

, (A9)

from which:

. (A10)

As can be expressed in the following three ways:

,

then, from these three expressions and from expression (A10) one can deduce that:

, (A11)

and as a result:

. (A12)

With the goal of verifying whether, of the two possible solutions given by expression (A10), only the one obtained with the positive sign ?? is valid, in the following we shall distinguish four cases (in terms of the values which Δ can take). It is understood that here Δ can refer to a known value (such as when contrasting the null hypotheses vs., in which case) or an unknown value which still has to be estimated (in which case):

1) When, in expression (A8) the following must occur. The solution then implies that which contradicts the second expression (A12). Thus, the appropriate solution is.

2) When, then from the first expression (A11); hence and. Again, the solution should be the second, given that it is the only one that is compatible with the restriction, a restriction which indicates that B = n. For this reason:

. (A13)

3) When, then, using the second expression (A12). Because this can only occur when, then and, and this implies that and that (so that). Because and, expression (A2) indicates that, then the solution is only possible when, that is, when. Again is the solution sought.

4) Finally, when, expression (A9) is a linear Equation in whose solution is given by ; and because, then:

. (A14)

Because in this case, from expression (A11), then and. Again the solution is not the correct one, while the solution yields a non-determination which we shall refer to in the following section.

As the solution is always, and because then by increasing by i in expression (A10) one obtains:

. (A15)

when the goal is to estimate (a situation in which, as we will now see, will take a value which depends on), the previous Equation should be solved in respect of. When is known (as is the case when the hypotheses vs. are contrasted, in which case), then the goal will be to determine the value of and the Equation will have to be solved in respect of. In both cases, it is shown later that the solution is unique.

2. Estimation of the Parameter Δ

In this section it is understood that both the parameters π_i and the parameter D are unknown. Now, , which leads to two different situations.

When, it is considered that, which also produces two cases. If,

then whose maximum possible value for 1 is reached when (the remainder of the

are worth 0) and takes any value, when and the take any values. If, then ?because there cannot be two - and the maximum is reached in (where the take any values). In both cases there is some indeterminate estimator and the inferences about cannot be made. One way of solving the problem consists in increasing all the data by 0.5 (so that) and applying the result in the following paragraph.

When, by using expressions (A3) and (A5) the following deduction can be made:

. (A16)

By substituting this value in the Equations in the previous section the following results are obtained. By substituting in the expression in (A9), each π_i should verify that:

, (A17)

so that expression (A10) ?which, as we know, only makes sense for the sign “+”? indicates that:

. (A18)

As a result, the Equation (A15) becomes:

, (A19)

which, because it is necessary to resolve this in, can be written more explicitly as follows:

. (A20)

Once the value of has been determined (which will be), by substituting for it in (A18) the value for the will be obtained. Similarly, by substituting the expression (A16) in the expressions (A3) to (A6) and (A8) one obtains, respectively:

(A21)

Finally, the inequality (A7) and the fact that the numerator in the first expression (A21) should be positive indicate, respectively, that:

(A22)

3. Unicity of Solutions

In order to see that the solution to Equation (A20) is unique, let us look at the function defined by expression (A19). When it can be seen that, so that the function always verifies the origin. Moreover, at the extremes of the range of Δ indicated by expression (4), always: when, because from expression (A22), so that and thus; by analogy, when

then, and. On the other

hand the function is convex with respect to because, from which it can be deduced that the minimum for is reached in a unique belonging to the closed interval. The position of the minimum with respect to the origin is determined by the behaviour of in. Given that

, (A23)

if then decreases in the origin and the minimum is found between 0 and 1 (more specifically, between 0 and, for the reason that the numerator of the first expression (A20) ought to be larger than or equal to zero); if, then the minimum of is precisely; finally, if, then is a function increasing in the origin and the minimum is found between and 0.

Similarly, in order to see whether the solution to the Equation (A15) is unique, let us look at the function defined in it (here it is assumed that is a known value). When is and thus. In the following we must bear in mind that for the first expression of (A12)

. (A24)

Since, where, then the function

decreases because: 1) If,;2) If, through the second inequality in

expression (A12), and thus; 3). If, through the first inequality in ex-

pression (A22), and hence because. As a result of this, has a unique solution in.

Appendix III. Standard Error in the Estimators

With the aim of obtaining the matrix formed by the variances and covariances of the estimators of the parameters of the model, let us first determine their information matrix, which is formed

by the elements where given by:

(A25)

where:

. (A26)

Given the type of sampling adopted (the values for r_i are previously fixed), the following must occur:

and. Hence:

(A27)

And by defining and as in expression (12), one obtains

(A28)

where is the Kronecker delta.

In order to determine in the following let us look at the division into blocks

, (A29)

where obviously is a scalar, is a column vector and is a square (symmetric) matrix of the order whose elements are defined by expressions (A27) and (A28) respectively. The determinant of is given by. Given that is the Schur complement of (cf. Meyer, 2000; p. 475), it can then be verified that. Because, one then obtains

. (A30)

In order to determine let us express the elements in defined in (A28) as, which allows us to split up this matrix in the sum, where and, the inverse of which is given by the Sherman-Morrison formula [24] , which produces

(A31)

where. When, in this expression, one looks at the terms defined in expression (12), the result is that is formed by the elements.

By substituting the obtained in (A30) one obtains an explicit expression for. From this (by algebraic manipulation) one arrives at the expression expanded in (10), which covers all the extended sums as far as (instead of doing so up to following the direct expansion of expression (A30)).

The other elements of are obtained by block matrix inversion of following what was shown in (A31): because the product is the identity matrix of the order, we obtain

, (A32)

. (A33)

By operating in both expressions one finds that the?component of is:

, (A34)

while consists of the elements

. (A35)

Obviously, the elements of the diagonal of are, and its expanded and simplified expression is the one given in expression (11).

The substitution of the unknown parameters with their respective estimators produces the corresponding esti-

mators for the variances; i.e., and.

It should be pointed out that the magnitude of is determined (in part) by the value of the quadratic form, which is defined as positive because the defined in expression (12) are positive for any. Because the character of is the same that of its inverse and the principal minors in this last matrix are

,

the proposed result is thus obtained. Therefore, the minimum value for is obtained

when, which is only possible if all the elements in are null, that is, if.

NOTES

^*Corresponding author.