Open Journal of Statistics
Vol.4 No.5(2014), Article ID:48771,12 pages
DOI:10.4236/ojs.2014.45035
Mixture Regression Estimators Using Multi-Auxiliary Variables and Attributes in Two-Phase Sampling
John Kung’u, Grace Chumba, Leo Odongo
Department of Mathematics, Kenyatta University, Nairobi, Kenya
Email: johnkungu08@yahoo.com, chumbagrace@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 23 May 2014; revised 26 June 2014; accepted 10 July 2014
ABSTRACT
In this paper, we have developed estimators of finite population mean using Mixture Regression estimators using multi-auxiliary variables and attributes in two-phase sampling and investigated its finite sample properties in full, partial and no information cases. An empirical study using natural data is given to compare the performance of the proposed estimators with the existing estimators that utilizes either auxiliary variables or attributes or both for finite population mean. The Mixture Regression estimators in full information case using multiple auxiliary variables and attributes are more efficient than mean per unit, Regression estimator using one auxiliary variable or attribute, Regression estimator using multiple auxiliary variable or attributes and Mixture Regression estimators in both partial and no information case in two-phase sampling. A Mixture Regression estimator in partial information case is more efficient than Mixture Regression estimators in no information case.
Keywords: Regression Estimator, Multiple Auxiliary Variables, Multiple Auxiliary Attributes, Two-Phase Sampling, Bi-Serial Correlation Coefficient

1. Introduction
The history of using auxiliary information in survey sampling is as old as the history of survey sampling. The work of Neyman [1] may be referred to as the initial work where auxiliary information has been used to estimate population parameters. Hansen and Hurwitz [2] also suggested the use of auxiliary information in selecting the sample with varying probabilities. The concept of ratio estimation was introduced in sample survey by Cochran [3] ; it is preferred when the study variable is highly positively correlated with the auxiliary variable. Watson [4] used the regression estimator of leaf area on leaf weight to estimate the average area of the leaves on a plant. Olkin [5] was the first person using information on more than one supplementary character, which is positively correlated with the variable under study, using a linear combination of ratio estimator based on each auxiliary variable. Raj [6] suggested a method of using multi-auxiliary information in sample survey.
The concept of double sampling was first proposed by Neyman [1] in sampling human populations when the mean of auxiliary variable was unknown. It was later extended to multiphase by Robson [7] . Abdul, Zahoor and Hanif [8] also developed a generalized multivariate regression estimator for multi-phase sampling using multiauxiliary variables. Zahoor, Abdul, and Muhhamad [9] suggested a generalized regression-cum-ratio estimator for two-phase sampling using multiple auxiliary variables. It is advantageous when the gain in precision is substantial as compared to the increase in the cost due to collection of information on the auxiliary variate for large samples. It was proved that optimum estimator in the proposed class of estimators was approximately equally efficient with the usual biased linear regression estimator. Samiuddin and Hanif [10] introduced ratio and regression estimation procedures for estimating population mean in two-phase sampling for different three situations depending upon the availability of information on two auxiliary variables for population. They considered three situations, first when information on both auxiliary variables was not available, second when information on one auxiliary variable was available and third, when information was available on both auxiliary variables.
Jhajj, Sharma and Grover [11] proposed a family of estimators using information on auxiliary attribute. They used known information of population proportion possessing an attribute (highly correlated with study variable Y). The optimum estimate of the proposed family of mean was less biased and more efficient than mean per unit estimator. The attribute is normally used when the auxiliary variable is not available e.g. an amount of milk produced and a particular breed of cow or an amount of yield of wheat and a particular variety of wheat. The estimator performed better than the usual sample mean and Naik and Gupta [12] estimator. Rajesh Pankaj, Nirmala and Florentins [13] used the auxiliary attribute in regression-ratio type exponential estimator following the work of Bahl and Tuteja [14] ; the estimator was more efficient compared to mean per unit, ratio and product type exponential estimator as well as Naik and Gupta [12] estimator.
Hanif, Haq and Shahbaz [15] proposed a general family of estimators using multiple auxiliary attribute in single and double phase sampling. The estimator had a smaller MSE compared to that of Jhajj, Sharma and Grover [11] . They also extended their work to ratio and regression estimator which was generalization of Naik and Gupta [12] estimator in single and double phase sampling with full information, partial information and no information. Moeen, Shahbaz and HanIf [16] proposed a class of mixture ratio and regression estimators for single phase sampling for estimating population mean by using information on auxiliary variables and attributes simultaneously. Kung’u and Odongo [17] and [18] proposed ratio-cum-product estimators using multiple auxiliary attributes in single and two-phase sampling.
In our paper, we will extend the mixture regression estimator proposed by Moeen, Shahbaz and HanIf [16] to two-phase sampling under full, partial and no information case strategies introduced by Samiuddin and Hanif [10] and also incorporate Arora and Bansi [19] approach in writing down the mean squared error.
2. Preliminaries
2.1. Notation and Assumption
Consider a population of N units. Let Y be the variable for which we want to estimate
the population mean and
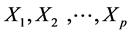 are p auxiliary variables. For two-phase sampling design let
are p auxiliary variables. For two-phase sampling design let
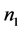 and
and
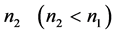 are sample sizes for first and second phase respectively.
are sample sizes for first and second phase respectively.
 and
and
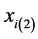 denote the
denote the
![]() auxiliary variables form first and second phase samples respectively and
auxiliary variables form first and second phase samples respectively and
![]() denote the variable of interest from second phase.
denote the variable of interest from second phase.
![]() and
and
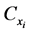 denote the population means and coefficient of variation of
denote the population means and coefficient of variation of
![]() auxiliary variables respectively and
auxiliary variables respectively and
 denotes the population correlation coefficient of Y and
denotes the population correlation coefficient of Y and![]() .
.
Further, let
 (1.0)
(1.0)
where ,
,
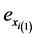 and
and
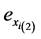 are sampling error and are very small. We assume that
are sampling error and are very small. We assume that
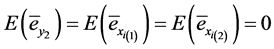 (1.1)
(1.1)
Consider a sample of size n drawn by simple random sampling without replacement
from a population of size N. Let
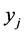 and denotes the observations on variable y and r respectively for the
and denotes the observations on variable y and r respectively for the
![]() unit where
unit where![]() .
.
In defining the attributes we assume complete dichotomy so that;
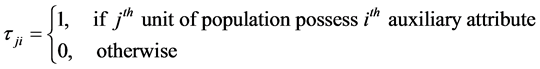 (1.2)
(1.2)
Let
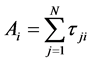 and
and
 be the total number of units in the population and sample respectively possessing
attribute
be the total number of units in the population and sample respectively possessing
attribute![]() . Let
. Let
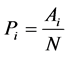 and
and
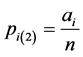 be the corresponding proportion of units possessing a specific attributes
be the corresponding proportion of units possessing a specific attributes
![]() and
and
![]() is the mean of the main variable at second phase. Let
is the mean of the main variable at second phase. Let
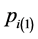 and
and
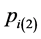 denote the
denote the
![]() auxiliary attribute form first and second phase samples respectively and
auxiliary attribute form first and second phase samples respectively and
![]() denote the variable of interest from second phase. The mean of main variable of
interest at second phase will be denoted by
denote the variable of interest from second phase. The mean of main variable of
interest at second phase will be denoted by![]() . Also let us define
. Also let us define
 (1.3)
(1.3)
The coefficient of variation and correlation coefficient are given by

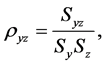
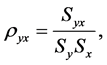

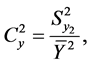
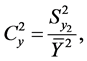 and
and
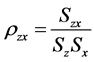
Then for simple random sampling without replacement for both first and second phases we write by using phase wise operation of expectations as:
 (1.4)
(1.4)
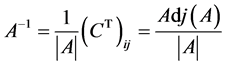 (1.5)
(1.5)
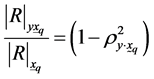 Arora and Lai [19] (1.6)
Arora and Lai [19] (1.6)
The following notations will be used in deriving the mean square errors of proposed estimators
 Determinant of population correlation matrix of variables
Determinant of population correlation matrix of variables .
.
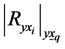 Determinant of
Determinant of
![]() minor of
minor of
 corresponding to the
corresponding to the
![]() element of
element of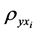 .
.
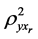 Denotes the multiple coefficient of determination of y
on
Denotes the multiple coefficient of determination of y
on .
.
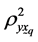 Denotes the multiple coefficient of determination of y on
Denotes the multiple coefficient of determination of y on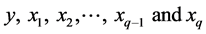 .
.
 Determinant of population correlation matrix of variables
Determinant of population correlation matrix of variables .
.
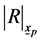 Determinant of population correlation matrix of variables
Determinant of population correlation matrix of variables .
.
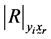 Determinant of the correlation matrix of
Determinant of the correlation matrix of .
.
 Determinant of the correlation matrix of
Determinant of the correlation matrix of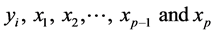 .
.
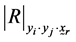 Determinant of the minor corresponding to
Determinant of the minor corresponding to
 of the correlation matrix of
of the correlation matrix of
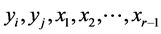 and
and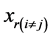 .
.
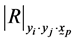 Determinant of the minor corresponding to
Determinant of the minor corresponding to
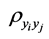 of the correlation matrix of
of the correlation matrix of
![]() (1.7)
(1.7)
2.2. Mean per Unit in Two-Phase Sampling
The sample mean
![]() using simple random sampling without replacement in two phase sampling is given
by is given by,
using simple random sampling without replacement in two phase sampling is given
by is given by,
 (2.0)
(2.0)
While its variance is given,
![]() (2.1)
(2.1)
2.3. Regression Estimators Using One and Multiple Auxiliary Variables and Attributes
Let
 and
and
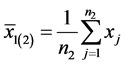 be the unbiased estimator of sample means of
be the unbiased estimator of sample means of
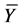 and
and
![]() respectively in two phase sampling. The simple regression estimator for known X
suggested by Watson [4] is,
respectively in two phase sampling. The simple regression estimator for known X
suggested by Watson [4] is,
 (2.2)
(2.2)
Its mean squared error is given by,
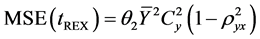 (2.3)
(2.3)
In case of multiple auxiliary variables, regression estimator is given by,
 (2.4)
(2.4)
Its mean squared error is given by,
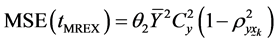 (2.5)
(2.5)
Naik and Gupta [12] defined Regression estimator of population when the prior information of population proportion of units, possessing the same attribute is variable as,
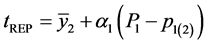 (2.6)
(2.6)
Its mean squared error is given by,
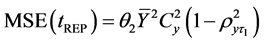 (2.7)
(2.7)
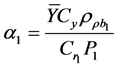 are optimum for Regression estimator.
are optimum for Regression estimator.
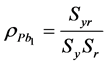 is the bi-serial correlation coefficient.
is the bi-serial correlation coefficient.
In case of multiple auxiliary variables, regression estimator is given by,
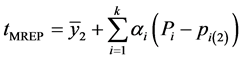 (2.8)
(2.8)
Its mean squared error is given by,
 (2.9)
(2.9)
The mixture ratio estimator based on multiple auxiliary variables and attributes by Moeen, Shahbaz and HanIf [16] is given by:
 (3.0)
(3.0)
It is normally known that the above estimators are biased but the bias being of
the order , can be assumed negligible in large samples.
It is assumed that the sample of size n is large enough so that the biases of these
estimators are negligible.
, can be assumed negligible in large samples.
It is assumed that the sample of size n is large enough so that the biases of these
estimators are negligible.
Our project will extend the mixture regression estimator proposed by Moeen, Shahbaz and Hanif [16] to twophase sampling under full, partial and no information case strategies introduced by Samiuddin and Hanif [10] .
3. Methodology
3.1. Proposed Mixture Regression Estimator in Two-Phase Sampling (Full Information Case)
If we estimate a study variable when information on all auxiliary variables and attributes is available from population, it is utilized in the form of their means. By taking the advantage of Mixture Regression estimator technique for two-phase sampling, a generalized estimator for estimating population mean of study variable Y with the use of multi auxiliary variables and attributes is suggested as:
 (3.0)
(3.0)
Substituting Equation (1.0) and (1.3) in (3.0), we get,
 (3.2)
(3.2)
The mean squared error of
![]() is given by
is given by
 (3.3)
(3.3)
We differentiate the Equation (3.3) partially with respect to
 and
and
 then equate to zero, using (1.4), (1.5), (1.6) and (1.7), we get
then equate to zero, using (1.4), (1.5), (1.6) and (1.7), we get
 (3.4)
(3.4)
 (3.5)
(3.5)
Using normal equation that is used to find the optimum values given (3.3), we can write (3.3) as,
 (3.6)
(3.6)
 (3.7)
(3.7)
Taking expectation in (3.7) and substituting (1.4), we get,
 (3.8)
(3.8)
Or
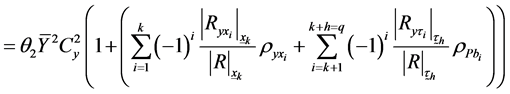 (3.9)
(3.9)
Or
 (3.10)
(3.10)
Or
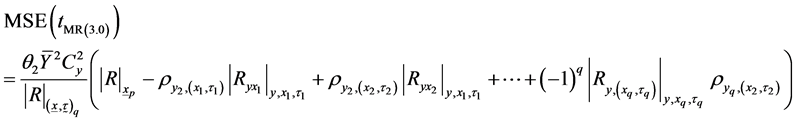 (3.11)
(3.11)
Or
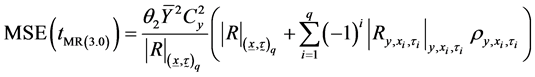 (3.12)
(3.12)
Or
 (3.13)
(3.13)
Using (1.6) in (3.13), we get
 (3.14)
(3.14)
3.2. Mixture Regression Estimator in Two-Phase Sampling (Partial Information Case)
In this case suppose, we have no information on all t auxiliary variables and h auxiliary attributes from population. Considering Mixture Regression estimator technique, the population mean of study variable Y can be estimated for two-phase sampling using multi-auxiliary variables and attributes as:
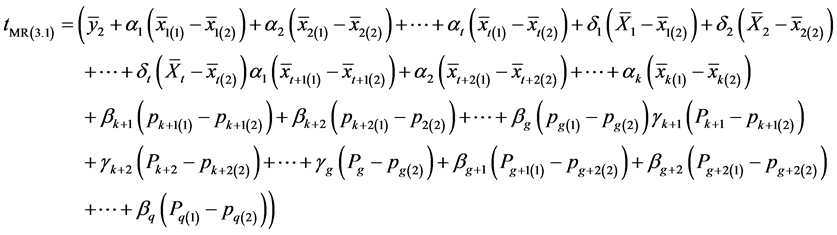 (3.15)
(3.15)
Substituting (1.0) and (1.3) in (3.15), we get,
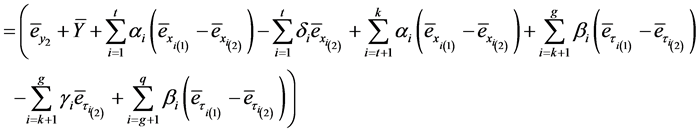 (3.16)
(3.16)
Mean squared error of
![]() estimator is given by
estimator is given by
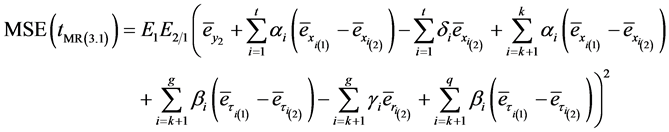 (3.17)
(3.17)
We differentiate the Equation (3.24) with respect to



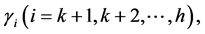
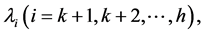
 and equate to zero and use (1.6) and (1.7). The optimum value is as follows,
and equate to zero and use (1.6) and (1.7). The optimum value is as follows,
 (3.18)
(3.18)
Using normal equation that are used to find the optimum values given (3.17) we can write
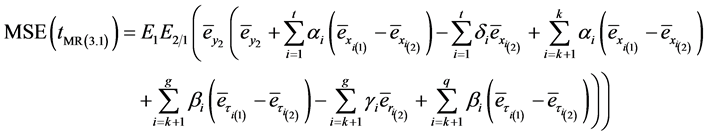 (3.19)
(3.19)
Or
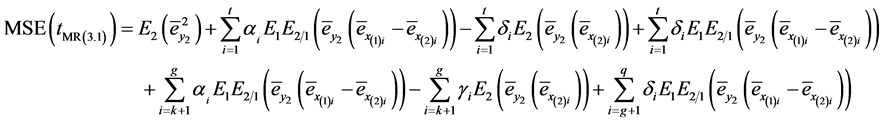 (3.20)
(3.20)
Using (1.4) in (3.28) we get,
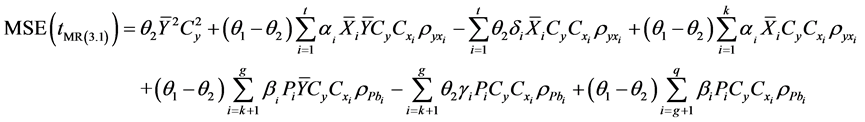 (3.22)
(3.22)
Or
 (3.23)
(3.23)
Or
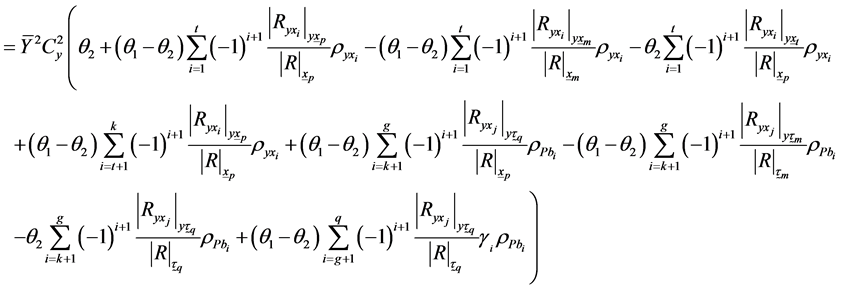 (3.24)
(3.24)
Or
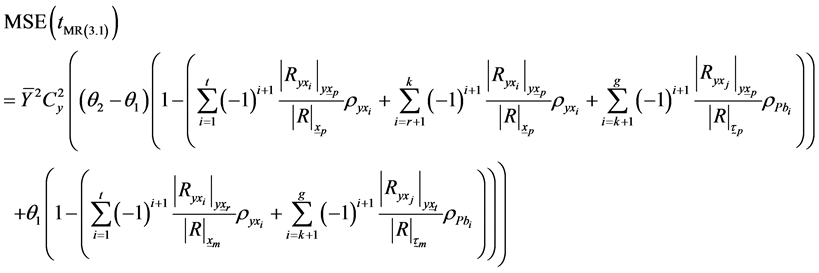 (3.25)
(3.25)
Or
 (3.26)
(3.26)
Or
 (3.27)
(3.27)
Using (1.6) in (3.27), we get
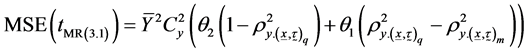 (3.28)
(3.28)
3.3. Mixture Regression Estimator in Two-Phase Sampling (No Information Case)
If we estimate a study variable when information on all auxiliary variables is unavailable from population, it is utilized in the form of their means. By taking the advantage of Mixture Regression estimator technique for twophase sampling, a generalized estimator for estimating population mean of study variable Y with the use of multi auxiliary variables and attributes is suggested as:
 (3.29)
(3.29)
Substituting equation (1.0) and (1.1) in (3.29), we get,
 (3.30)
(3.30)
The mean squared error of
 is given by,
is given by,
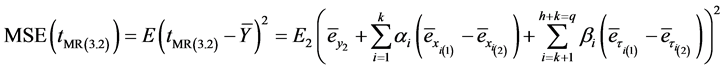 (3.31)
(3.31)
We differentiate the Equation (3.32) partially with respect to
 and
and
 then equate to zero, using (1.4), (1.5), (1.6) and (1.7), we get
then equate to zero, using (1.4), (1.5), (1.6) and (1.7), we get
 (3.32)
(3.32)
 (3.33)
(3.33)
Using normal equation that is used to find the optimum values given (3.31) we can write,
 (3.34)
(3.34)
 (3.35)
(3.35)
Taking expectation and substituting (3.32) and (3.33) and, we get,
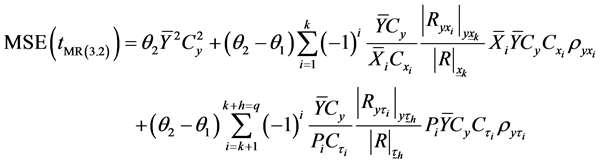 (3.36)
(3.36)
Or
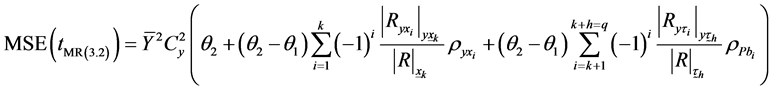 (3.37)
(3.37)
Or
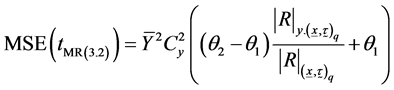 (3.38)
(3.38)
Using (1.6) in (3.38), we get,
 (3.39)
(3.39)
Simplifying (3.38) we get,
 (3.40)
(3.40)
3.4. Bias and Consistency of Mixture Regression Estimators
These mixture regression estimators using multiple auxiliary variables in two phase sampling are biased. However, these biases are negligible for moderate and large samples. It’s easily shown that the mixture regression estimators are consistent estimators using multiple auxiliary variables since they are linear combinations of consistent estimators it follows that they are also consistent.
4. Result and Discussion
In this section, we carried out some data analysis using R statistical package to compare the performance of mixture regression estimators with already existing estimator in two-phase sampling for finite population that uses one or multiple auxiliary variables or attributes.
In the natural population, the study variable was body fat and auxiliary variables are Thigh circumference and chest circumference while attributes were abdomen and hip circumference.
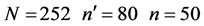
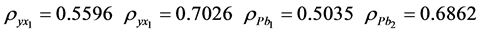
Population: The simulated population was a normally distributed with the following
parameters![]() ,
,
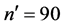 ,
,
![]() mean = 75 standard deviation = 5
mean = 75 standard deviation = 5
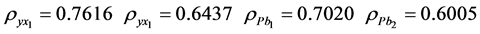
All the results were obtained after carrying out several random sample and taking the average.
In order to evaluate the efficiency gain we could achieve by using the proposed estimators, we have calculated the variance of mean per unit and the mean squared error of all estimators we have considered. We have then calculated percent relative efficiency of each estimator in relation to variance of mean per unit. We have then compared the percent relative efficiency of each estimator, the estimator with the highest percent relative efficiency is considered to be the most efficient than the other estimator. The percent relative efficiency is calculated using the following formulae.
 (4.0)
(4.0)
The Table 1 shows percent relative efficiency of proposed and existing estimator with respect to mean per unit estimator for two phase sampling. It is observed that Regression estimators using one auxiliary variables and attributes are more efficient than mean per unit in the two populations. Again, Regression estimators using multiple auxiliary variables and attributes are more efficient than mean per unit and Regression estimators. Finally, Mixture Regression estimators using multiple auxiliary variables and attributes is the most efficient of the five estimators in the two populations since it has the highest percent relative efficiency.
Finally, Table 2 compares the efficiency of full information case and partial case to no information case and full to partial information case. It is observed that the full information case and partial information case are more efficient than no information case because they have higher percent relative efficiency than no information case. In addition, the full information case is more efficient than the partial information case because it has a higher percent relative efficiency than partial information case.
5. Conclusions
The percent relative efficiency is used in sample survey to compare the efficiency of different estimators. The estimator with the highest percent relative efficiency with respect to mean per unit is normally considered to be more efficient compared to the other estimators.
According to Table 1, the proposed Mixture Regression estimators using multiple auxiliary variables and attributes in two-phase sampling has the highest percent relative efficiency compared to mean per unit, Regression estimators using one auxiliary variable and attributes, Regression estimators using multiple auxiliary variables and attributes. This means that the ratio-cum-product estimator in two-phase sampling is the most efficient estimator compared to the estimators that utilize auxiliary variables and attributes.
The Mixture Regression estimators were then extended to two-phase sampling in partial and no information case. In Table 2, we compared the efficiency of full and partial information case to no information case and
Table 1 . Relative efficiency of suggested estimator with respect to mean per unit estimator for two phase sampling.
Table 2. Comparisons of full, partial and no information cases for proposed mixture regression estimator.
found that the two are more efficient than the no information case. We also compared the efficiency of full information case to partial information case and found that the full information case is more efficient than the partial information case.
The proposed Mixture Regression estimator using multiple auxiliary variables and attributes in two-phase sampling is recommended to estimate the finite populations mean for full information case as it outperforms all the other existing estimators for full information using one auxiliary or multiple auxiliary variables and attributes. It also outperforms Mixture Regression estimators using multiple auxiliary variables and attributes in partial and no information cases.
When some auxiliary variables are unknown, the two-phase sampling is recommended. If some auxiliary variables are known, the Mixture Regression estimators using multiple auxiliary variables and attributes in partial information case should be used but if all the auxiliary variables and attributes are unknown. Mixture Regression estimators using multiple auxiliary variables in no information case should be used to estimate the finite population mean.
References
- Neyman, J. (1938) Contribution to the Theory of Sampling Human Populations. Journal of the American Statistical Association, 33, 101-116. http://dx.doi.org/10.1080/01621459.1938.10503378
- Hansen, M.H. and Hurwitz, W.N. (1943) On the Theory of Sampling from Finite Populations. Annals of Mathematical Statistics, 14, 333-362. http://dx.doi.org/10.1214/aoms/1177731356
- Cochran, W.G. (1940) The Estimation of the Yields of the Cereal Experiments by Sampling for the Ratio of Grain to Total Produce. Journal of Agricultural Science, 30, 262-275. http://dx.doi.org/10.1017/S0021859600048012
- Watson, D.J. (1937) The Estimation of Leaf Areas. Journal of Agricultural Science, 27, 474.http://dx.doi.org/10.1017/S002185960005173X
- Olikin, I. (1958) Multivariate Ratio Estimation for Finite Population. Biometrika, 45, 154-165.http://dx.doi.org/10.1093/biomet/45.1-2.154
- Raj, D. (1965) On a Method of Using Multi-Auxiliary Information in Sample Surveys. Journals of the American Statistical Association, 60, 154-165. http://dx.doi.org/10.1080/01621459.1965.10480789
- Robson, D.S. (1952) Multiple Sampling of Attributes. Journal of the American Statistical Association, 47, 203-215.http://dx.doi.org/10.1080/01621459.1952.10501164
- Zahoor, A., Muhhamad, H. and Munir, A. (2009) Generalized Multivariate Ratio Estimator Using Multiple Auxiliary Variables for Multi-Phase Sampling. Pakistan Journal of Statistic, 26, 569-583.
- Zahoor, A., Muhhamad, H. and Munir, A. (2009) Generalized Regression-Cum-Ratio Estimators for Two Phase Sampling Using Multiple Auxiliary Variables. Pakistan Journal of Statistics, 25, 93-106.
- Simiuddin, M. and Hanif, M. (2007) Estimation of Population Mean in Single and Two Phase Sampling with or without Additional Information. Pakistan Journal of Statistics, 23, 99-118.
- Jhajj, H.S., Sharma, M.K. and Grover, L.K. (2006) A Family of Estimator of Population Mean Using Information on Auxiliary Attributes. Pakistan Journal of Statistics, 22, 43-50.
- Naik, V.D. and Gupta, P.C. (1996) A Note on Estimation of Mean with Known Population of Auxiliary Character. Journal of the Indian Society of Agricultural Statistics, 48, 151-158.
- Rajesh, S., Pankaj, C., Nirmala, S. and Florentins, S. (2007) Ratio-Product Type Exponential Estimator for Estimating Finite Population Mean Using Information on Auxiliary Attributes. Renaissance High Press, USA.
- Bahl, S. and Tuteja, R.K. (1991) Ratio and Product Type Estimator. Information and Optimization Science, 12, 159-163. http://dx.doi.org/10.1080/02522667.1991.10699058
- Hanif, M., Haq, I.U. and Shahbaz, M.Q. (2009) On a New Family of Estimator Using Multiple Auxiliary Attributes. World Applied Science Journal, 11, 1419-1422.
- Moeen, M., Shahbaz, Q. and HanIf, M. (2012) Mixture Ratio and Regression Estimators Using Multi-Auxiliary Variable and Attributes in Single Phase Sampling. World Applied Sciences Journal, 18, 1518-1526.
- Kung’u, J. and Odongo, L. (2014) Ratio-Cum-Product Estimator Using Multiple Auxiliary Attributes in Single Phase Sampling. Open Journal of Statistics, 4, 239-245. http://dx.doi.org/10.4236/ojs.2014.44023
- Kung’u, J. and Odongo, L. (2014) Ratio-Cum-Product Estimator Using Multiple Auxiliary Attributes in Two-Phase Sampling. Open Journal of Statistics, 4, 246-257. http://dx.doi.org/10.4236/ojs.2014.44024
- Arora, S. and Bansi, Lal. (1989) New Mathematical Statistics. Satya Prakashan, New Delhi.


