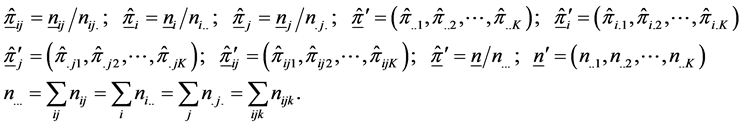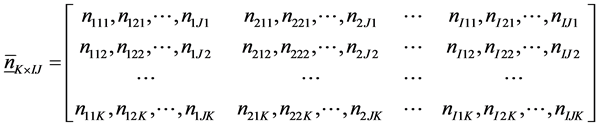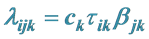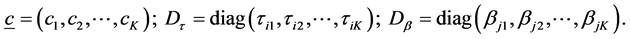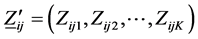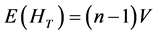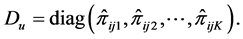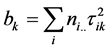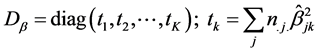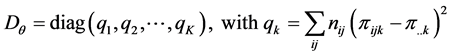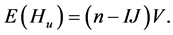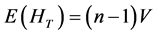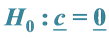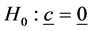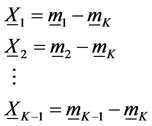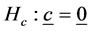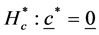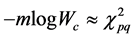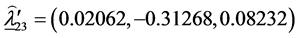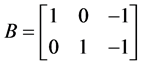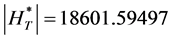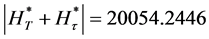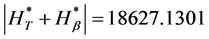Open Journal of Statistics
Vol.04 No.08(2014), Article ID:49939,10 pages
10.4236/ojs.2014.48055
A Multivariate Test for Three-Factor Interaction in 3-Way Contingency Table under the Multiplicative Model
Njoku O. Ama
Department of Statistics, University of Botswana, Gaborone, Botswana
Email: njoku52@gmail.com, amano@mopipi.ub.bw
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 June 2014; revised 22 July 2014; accepted 30 July 2014
ABSTRACT
Two test statistics that have been commonly used in analysing interactions in contingency table are the Pearson’s Chi-square statistic, χ2, and likelihood ratio test statistic, G2. Both test statistics, in tables with sufficiently large sample size, have an asymptotic chi-square distribution with degrees of freedom (df) equal to the number of free parameters in the saturated model. For example under the hypothesis of independence of the row and column conditioned on the layer in an I × J × K contingency table, the df is K(I − 1)(J − 1). These test statistics, in large sized tables, will have less power since they have large degrees of freedom. This paper proposes a product effect model, which combines the advantages of the multiplicative models over the additive, for analysing the interaction between the row and column of the 3-way table conditioned on the layer. The derived statistics is shown to be asymptotically chi-square with a small degree of freedom, K − 1, for the I × J × K contingency table. The performance of the developed statistic is compared with the Pearson’s chi-square statistic and the likelihood ratio statistic test using an illustrative example. The results show that the product effect test can detect interaction even when some of the main effects are not significant and can perform better than the other competitors having smaller degree of freedom in large sized tables.
Keywords:
Contingency Tables, Product Effect, Models, Interaction

1. Introduction
A 3-way contingency table is a cross-classification of observations by the levels of three categorical variables—A, B, and C. The levels can be ordinal or nominal. If n units in a sample are independently and identically distributed (IID); that is, if they constitute a random sample, then the vector of cell counts
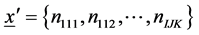 has a multinomial distribution with index
has a multinomial distribution with index
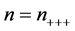 and a parameter,
and a parameter,
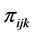 , where
, where
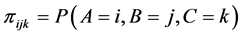 probability that a randomly selected unit falls into the
probability that a randomly selected unit falls into the
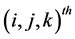 cell of the contingency table with variables A, B and C. The probability distribution
cell of the contingency table with variables A, B and C. The probability distribution
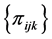 is the joint distribution of A, B, and C.
is the joint distribution of A, B, and C.
Interaction in the 3-way contingency has been tested using the chi-square statistic and the likelihood ratio test statistic with
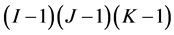 degree of freedom [1] -[3] . Grizzle et al. [4] , Darroch [5] and Johnson and Graybill [6] have modelled interaction as a product of the marginal effects or components of the ways of classification of the table. Tukey [7] in order to overcome the difficulty in testing for interaction in the two-factorial experiment with one observation per cell modelled the two-factor interaction as a product of the effects of the two factors and developed a one degree of freedom F-test for analysing the interaction between the factors. Drawing an analogy from the two factorial experiments we can view the 2-way contingency table as a two-factorial experiment with one observation per cell similar to the Poisson modelling of 2-way contingency table where the cell observations are seen as the mean number of occurrences of the event within a defined infinitesimal interval. The I × J × K contingency table can be viewed as K 2-way contingency table. The present paper argues that the transformation of the contingency table applicable in the likelihood ratio tests [1] [8] is often unnecessary but that the data can be analysed in a manner similar to the Pearson’s chi-square which does not transform the data. A multivariate approach is adopted in analysing the interaction in an I × J × K table, under the product effect model, where the three-factor interaction is defined as a product of the effects of the ways of classification of the table. The advantage of the proposed model is that it gives rise to chi-square tests with smaller degrees of freedom, irrespective of the size of the table, which is conjectured to have greater power than other tests with larger degrees of freedom. It has been shown [9] [10] that the power of the noncentral chi-square statistics, for a given value of non-centrality parameter and level of significance, increases as the degree of freedom decreases. Our results will be of some practical value to researchers who are involved in analysing mutual independence in higher order tables as their results will be based on small degrees of freedom leaving extra degrees of freedom for further decomposition of other forms of independence in the data. Extension of the proposed method to higher order tables is straightforward.
degree of freedom [1] -[3] . Grizzle et al. [4] , Darroch [5] and Johnson and Graybill [6] have modelled interaction as a product of the marginal effects or components of the ways of classification of the table. Tukey [7] in order to overcome the difficulty in testing for interaction in the two-factorial experiment with one observation per cell modelled the two-factor interaction as a product of the effects of the two factors and developed a one degree of freedom F-test for analysing the interaction between the factors. Drawing an analogy from the two factorial experiments we can view the 2-way contingency table as a two-factorial experiment with one observation per cell similar to the Poisson modelling of 2-way contingency table where the cell observations are seen as the mean number of occurrences of the event within a defined infinitesimal interval. The I × J × K contingency table can be viewed as K 2-way contingency table. The present paper argues that the transformation of the contingency table applicable in the likelihood ratio tests [1] [8] is often unnecessary but that the data can be analysed in a manner similar to the Pearson’s chi-square which does not transform the data. A multivariate approach is adopted in analysing the interaction in an I × J × K table, under the product effect model, where the three-factor interaction is defined as a product of the effects of the ways of classification of the table. The advantage of the proposed model is that it gives rise to chi-square tests with smaller degrees of freedom, irrespective of the size of the table, which is conjectured to have greater power than other tests with larger degrees of freedom. It has been shown [9] [10] that the power of the noncentral chi-square statistics, for a given value of non-centrality parameter and level of significance, increases as the degree of freedom decreases. Our results will be of some practical value to researchers who are involved in analysing mutual independence in higher order tables as their results will be based on small degrees of freedom leaving extra degrees of freedom for further decomposition of other forms of independence in the data. Extension of the proposed method to higher order tables is straightforward.
Model for 3-Factor Interaction
Let us assume that we have an I × J × K 3-way contingency, representing respectively the row, column and layer classifications of the table, and that the K-dimensional vector
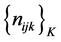 of frequency layers available in the
of frequency layers available in the
 cell has associated it with a K-dimensional vector
cell has associated it with a K-dimensional vector
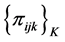 of unknown cell probabilities such that
of unknown cell probabilities such that
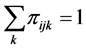 . In addition if we assume that
. In addition if we assume that
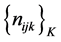 follows a multinomial probability distribution given by
follows a multinomial probability distribution given by
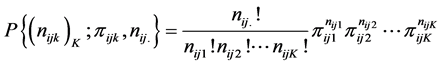 (1.1)
(1.1)
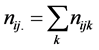 is fixed,
is fixed,

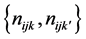 are independent for all
are independent for all
The 3-way contingency table under the multinomial structure described above is similar to the layout of a three-factorial experiment with one observation per cell. In the spirit of [7] and drawing an analogy from the factorial experimental structure, a linear additive model for the observed cell probability in the
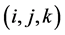
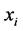
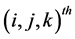
Under the assumption (1.1), and given the
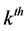
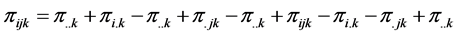
where,
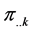
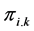
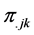
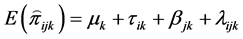
where,
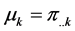
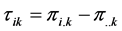
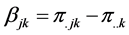
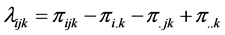
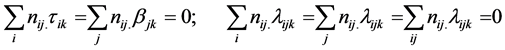
and are independent of the kth layer.
The relation (1.3) can be recast in vector notation as
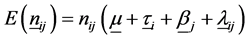
Or
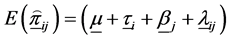
where,
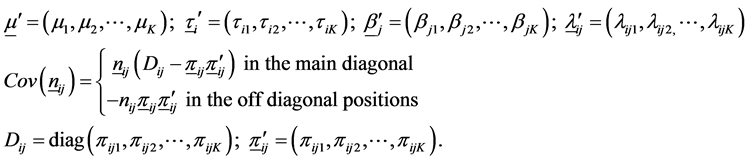
Estimation of the parameters of this model (1.6) by maximum likelihood proceeds by maximization of the multinomial likelihood (1.1) with the probabilities
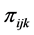
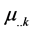
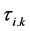
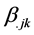
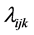
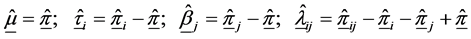
where,
The matrix
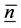
For the kth layer, the interaction between the ith row and jth column is defined multiplicatively as being proportional to the ith row effect and jth column effect and given as
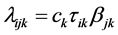
where, ck is an unknown constant for the layer;
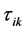
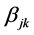
2. Development of Test Statistics Based on the Model
Rewriting (1.9), the model for the two-factor interaction for the kth layer response, in vector notation,
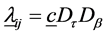
where
The matrix of interaction
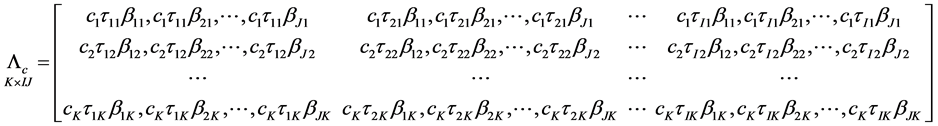
From (1.5) or (1.6) the residual after substituting (2.1) becomes
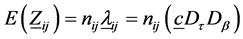
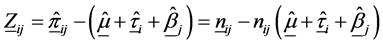
This gives the least square estimate
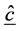
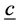
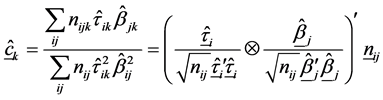
The matrix of sum of squares sum of product (SS-SP) for interaction from (2.3) is
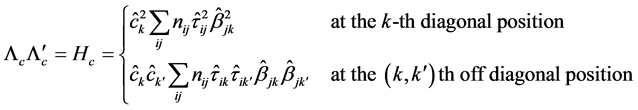
with expectation
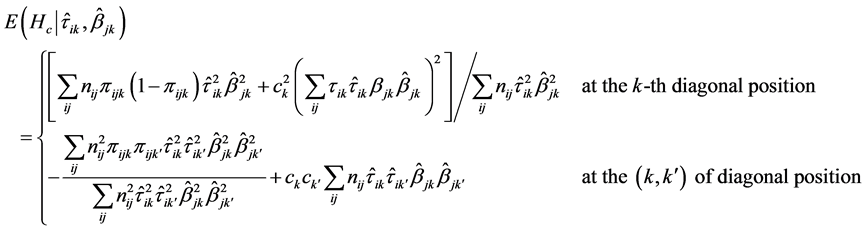
The total sum of squares and cross product (SS-SP) is given as
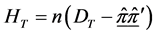
where,
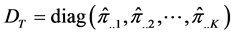
The expectation of
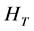
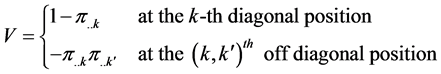
The total SS-SP matrix
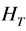
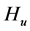
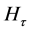
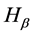
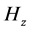
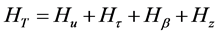
The unit SS-SP matrix
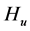
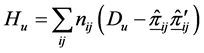
with
The expectation of
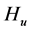
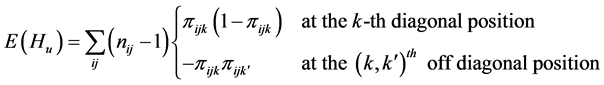
The matrix of SS-SP for the row effect,
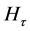
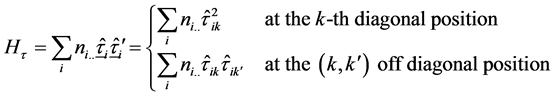
With expectation,
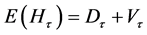
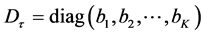

The matrix of SS-SP,
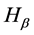
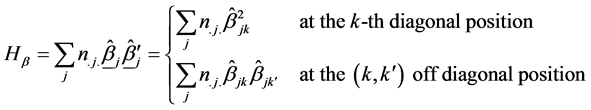
With expectation,
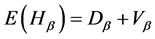
and

The matrix of SS-SP for the residual (2.3) is
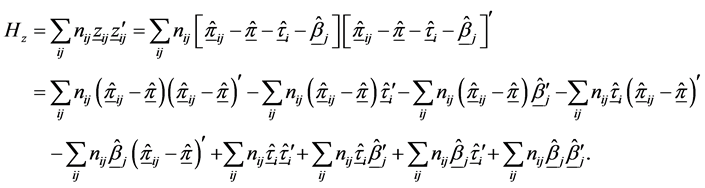
With expectation
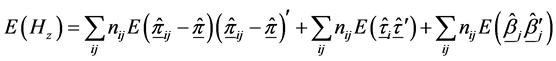
Since the cross-product terms will vanish on taking expectation because of independence and restriction in (1.4)
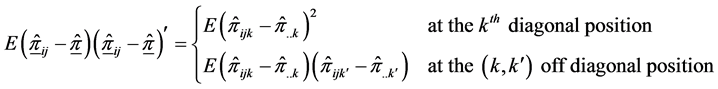
Hence,
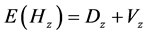
where,
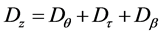
and
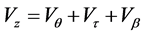
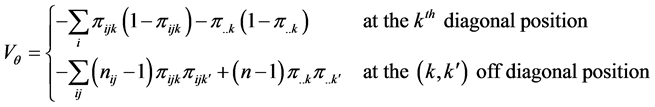
The hypothesis of no interaction,
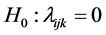
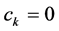
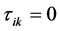
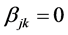
Hence
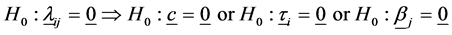
Under the null hypothesis (2.26), in which case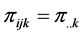
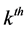
Similarly,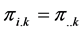
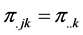
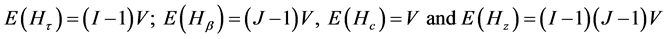
However, whether or not
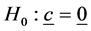
where V is as defined in (2.10). Each of the quantities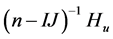
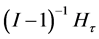
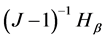
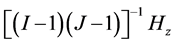
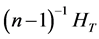
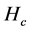
Independence of HT, Hc, Hτ, Hβ
By appealing to the following theorem [13] , it can be shown that the quadratic forms HT, Hc, Hτ and Hβ, are independent.
Theorem 2.1. Let
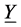
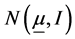
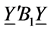
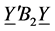
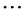
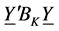
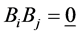
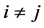
Theorem 2.2. As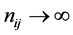
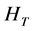
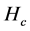
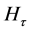
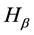
By theorem 1, the joint independence of HT, Hc, Hτ and Hβ implies pairwise independence.
3. Construction of Test Statistic for the Hypothesis
Recall that
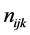
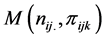
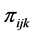
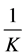
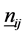
multivariate normal distribution with mean
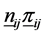
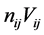
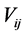
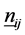
Under the hypothesis,
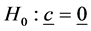

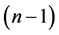
pendent of Hc. They can be used in constructing the determinant based test statistic for the hypothesis
Since the matrix V is nonsingular, by generating the matrix of contrasts, say B and pre- and post-multiplying each of them by B and B transpose, V can be made non-singular.
Let
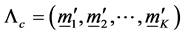
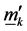
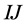
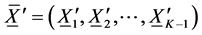
Then
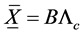
where

The matrix B is of full rank,
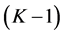
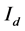
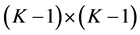
Certainly,
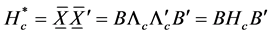
is a non-singular transformation of the matrix Hc and so also is the matrix
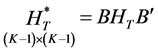
The hypothesis
is similarly transformed to
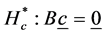
However, [14] and [15] have discussed the equivalence between
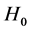
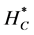
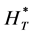
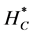
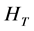
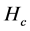
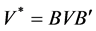
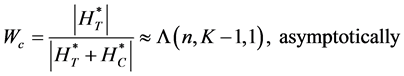
where
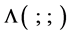
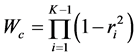
where
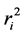
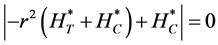
and
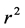
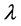
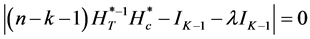
by the relation
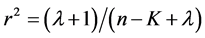
Under the null hypothesis,
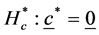
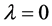
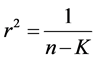
It has been shown, [16] , that
where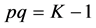
Thus,
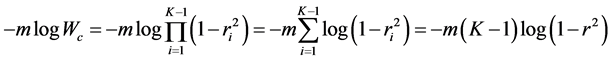
under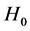
Asymptotically as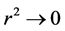
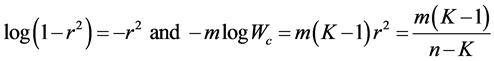
Hence
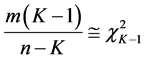
The best value of m for the expectation on both sides of (3.13) to be equal is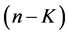
Therefore,
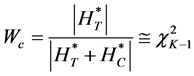
and can provide a test criterion for the rejection or non-rejection of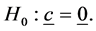
The test rejects the hull hypothesis if
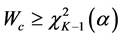
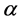
4. Illustrative Example
The application of the developed test makes use of data taken from [17] (see Table 1). The data represent the attitude of 333 undergraduate students of University of Nigeria towards taking up teaching as a profession after graduation. The students were sampled from three groups of faculties,
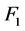
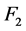
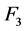
The estimates of the parameters in (1.5) are:
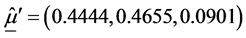
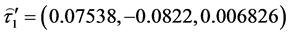
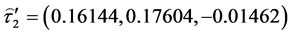
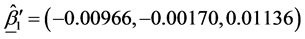
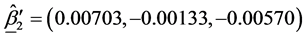
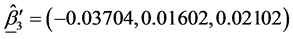
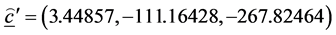
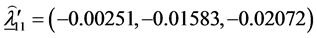
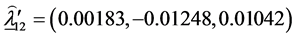
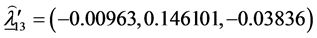
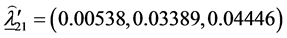
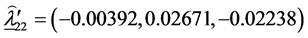
The matrix of SS-SP due to interaction,
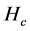
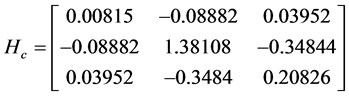
Therefore,
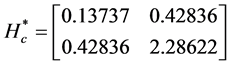
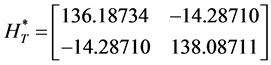
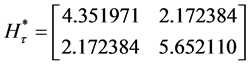
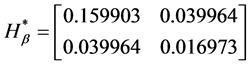
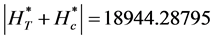
Similarly,
These values are summarized in the Table 2.
Table 1. Attitude of university students towards the teaching profession.
Table 2. Multanova of categorical data for attitude of students towards teaching.
m = 330.
The Pearson’s chi-square for testing the hypothesis of no interaction (independence of the row and column for the kth response),
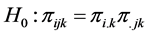
5. Conclusion
The results of the analysis show that while the effect of the sex and interaction are significant in the data, the effect of faculty is not significant. Thus, the proposed test for interaction based on the product effect model and based on 2 degrees of freedom
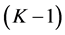
References
- Cheng, P.E., Liou, M. and Aston, J.A.D. (2009) Likelihood Ratio Tests with Three-Way Tables. Institute of Statistical Science, Academia Sinica 2CRiSM, Department of Statistics, The University of Warwick, UK. http://www3.stat.sinica.edu.tw/library/c_tec_rep/2007-3-20090206.pdf
- Agresti, A. (2002) Categorical Data Analysis. 2nd Edition, John Wiley and Sons Inc., Hoboken, 132. http://dx.doi.org/10.1002/0471249688
- Christensen, R. (1997) Loglinear Models and Logistic Regression. 2nd Edition, Springer-Verlag, New York Inc., New York.
- Grizzle, J.E., Starmer, F. and Koch, G.G. (1969) Analysis of Categorical Data by Linear Models. Biometrics, 25, 489- 504. http://dx.doi.org/10.2307/2528901
- Darroch, J.N. (1962) Interactions in Multi-Factor Contingency Tables. Journal of the Royal Statistical Society, B24, 251-263.
- Johnson, D.E. and Graybill, F.A. (1972) An Analysis of a Two-Way Model with Interaction and No Replication. Journal of the American Statistical Association, 67, 862-868. http://dx.doi.org/10.1080/01621459.1972.10481307
- Tukey, T.W. (1949) One Degree of Freedom for Non-Additivity. Biometrics, 5, 232-242. http://dx.doi.org/10.2307/3001938
- Cheng, P.E., Liou, M. and Aston, J.A.D. (2010) Likelihood Ratio Tests with Three-Way Tables. Journal of the American Statistical Association, 105, 740-749. http://dx.doi.org/10.1198/jasa.2010.tm09061
- Ama, N.O. (1991) On Multiplicative Models for Interaction in Contingency Tables. Unpublished Ph.D. Thesis, University of Nigeria, Nsukka.
- Hélie, S. (2007) Understanding Statistical Power Using Noncentral Probability Distributions: Chi-Squared, G-Squared, and ANOVA. Tutorials in Quantitative Methods for Psychology, 3, 63-69.
- Lancaster, H.O. (1969) The Chi-Squared Distribution. Wiley & Sons, Inc., New York.
- Darroch, J.N. (1974) Multiplicative and Additive Interaction in Contingency Tables. Biometrika, 61, 207-214. http://dx.doi.org/10.1093/biomet/61.1.207
- Graybill, F.A. (1961) An Introduction to Linear Statistical Models. McGraw-Hill, New York.
- Mardia, K.V., Kent, J.T. and Bibby, J.M. (1979) Multivariate Analysis. Academic Press, London.
- Kshirsagar, A.M. (1972) Multivariate Analysis. Marcel Dekker, Inc., New York.
- Bartlett, M.S. (1938) Further Aspects of the Theory of Multiple Regression. Mathematical Proceedings of the Cambridge Philosophical Society, 34, 33-40. http://dx.doi.org/10.1017/S0305004100019897
- Onukogu, I.B. (1985) An Analysis of Variance of Nominal Data. Statistica, anno, XLIV, No. 1, 87-96.