Open Journal of Statistics
Vol. 3 No. 5 (2013) , Article ID: 37645 , 7 pages DOI:10.4236/ojs.2013.35037
Effect of Correlation Level on the Use of Auxiliary Variable in Double Sampling for Regression Estimation
Department of Mathematical Sciences, Olabisi Onabanjo University, Ago-Iwoye, Nigeria
Email: *bayoagunbiade@gmail.com
Copyright © 2013 Dawud Adebayo Agunbiade, Peter I. Ogunyinka. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 21, 2013; revised July 21, 2013; accepted July 28, 2013
Keywords: Correlation Level; Auxiliary Variable; Regression Estimator; Double Sampling and Relative Efficiency of Estimator
ABSTRACT
While an auxiliary information in double sampling increases the precision of an estimate and solves the problem of bias caused by non-response in sample survey, the question is that, does the level of correlation between the auxiliary information x and the study variable y ease in the accomplishment of the objectives of using double sampling? In this research, investigation was conducted through empirical study to ascertain the importance of correlation level between the auxiliary variable and the study variable to maximally accomplish the importance of auxiliary variable(s) in double sampling. Based on the Statistics criteria employed, which are minimum variance, coefficient of variation and relative efficiency, it was established that the higher the correlation level between the study and auxiliary variable(s) is, the better the estimator is.
1. Introduction
In sampling theory, auxiliary information may be utilized at any of these three stages or by combining two or all of the three stages. These stages are: (1) at the pre-selection stage or designing stage of the survey in stratifying the population; (2) at the sample selection stage; and (3) at the post-selection or estimation stage. In whatever case, the use of auxiliary information in sample survey is better than the case where no auxiliary information is utilized. Ratio, regression, product and difference estimators take advantage of auxiliary information at the estimation stage. However, when the population information is not known then double sampling method becomes necessary for estimation. [1] is of the opinion that estimation of required parameters can efficiently be done with ratio and regression methods of estimation with two-phase sampling or double sampling method. Double sampling for ratio estimation becomes necessary over double sampling for regression estimation if the data under consideration are well fitted by a straight line through the origin [2]. Among the authors who have recently contributed to the use of auxiliary variable(s) to establish various estimators for the population parameters are [3-5]. However, in both cases of ratio and regression estimations or the use of double sampling in ratio and regression estimations, there must exists positive correlation between the auxiliary variable 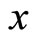 and study variable
and study variable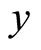 . This article, empirically, investigates to ascertain the importance of correlation level in the use of auxiliary variable in estimating the population parameter using double sampling for regression estimation method.
. This article, empirically, investigates to ascertain the importance of correlation level in the use of auxiliary variable in estimating the population parameter using double sampling for regression estimation method.
2. Methodology
2.1. The Regression Estimator
Let  be the sample values of the main character
be the sample values of the main character  and the auxiliary character
and the auxiliary character 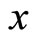 respectively obtained with simple random sampling without replacement (SRSWOR) of sample size
respectively obtained with simple random sampling without replacement (SRSWOR) of sample size 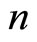 from the population size
from the population size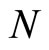 . The linear regression estimator of the mean as giving by [6] is:
. The linear regression estimator of the mean as giving by [6] is:
 (1)
(1)
where
 ; (2)
; (2)
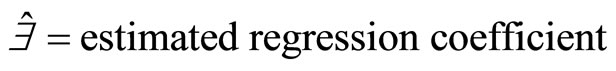


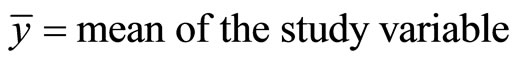
The mean square error (MSE) of  is giving as:
is giving as:
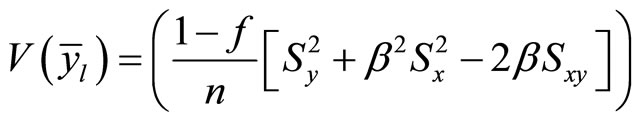 (3)
(3)
Similarly, the estimated mean square error (MSE) of 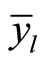 is giving as:
is giving as:
 (4)
(4)
expressing Equation (4) in terms of correlation coefficient; (where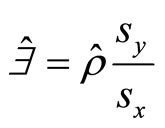 )
)
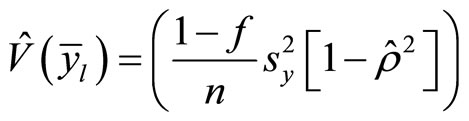 (5)
(5)
2.2. Double Sampling for Regression Estimator
The When double sampling for regression estimation is to be used, then there must exist non-zero interception of the regression line on the study variable axis of the scattered diagram. The double sampling linear regression estimator of population mean is giving as
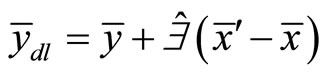 (6)
(6)
where
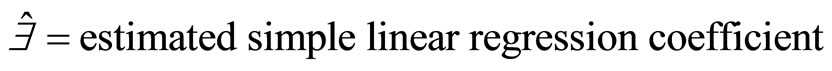
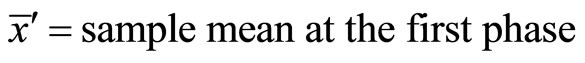
Reference [7], hence, presented the estimated variance of 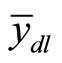 as
as
 (7)
(7)
Equation (7) can be expressed in terms of 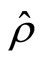 (where
(where ), this gives
), this gives
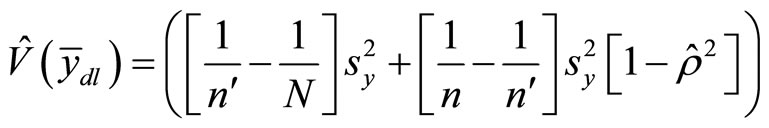 (8)
(8)
Similarly, [7] presented the optimum variance of double sampling regression estimator as:
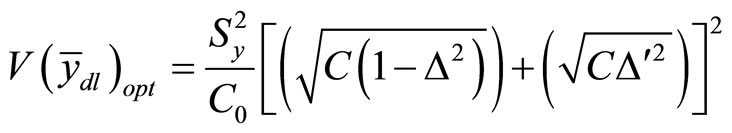 (9)
(9)
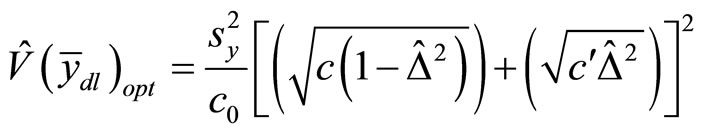 (10)
(10)
2.3. Correlation Coefficient and Coefficient of Determination
The simplest method for measuring the relationship existence between two variables (one dependent variable and one independent variable) is with the tool of correlation and regression analysis [8]. Correlation coefficient determines the degree of relationship between variables. It is linear when all parts  on a scattered diagram seem to lie near a straight line or it is nonlinear when all parts seem to lie near a curve. This work focuses on linear correlation. Correlation between variables can be measured with the use of different indices (coefficients). The three most popular of these indices are: Pearson’s Product-moment correlation, Spearman’s rank coefficient and kandall’s tau coefficients. Kendall’s tau established by [9] can be used as an alternative to spearman’s rank correlation coefficient for ranked data. [10] analysed the properties of kendall’s coefficient and states that “the coefficient we have introduced provides a kind of average measure of the agreement between pairs of numbers (“agreement”, that is to say, in respect of order) and thus has evident recommendation as a measure of the concordance between two rankings” and “In general,
on a scattered diagram seem to lie near a straight line or it is nonlinear when all parts seem to lie near a curve. This work focuses on linear correlation. Correlation between variables can be measured with the use of different indices (coefficients). The three most popular of these indices are: Pearson’s Product-moment correlation, Spearman’s rank coefficient and kandall’s tau coefficients. Kendall’s tau established by [9] can be used as an alternative to spearman’s rank correlation coefficient for ranked data. [10] analysed the properties of kendall’s coefficient and states that “the coefficient we have introduced provides a kind of average measure of the agreement between pairs of numbers (“agreement”, that is to say, in respect of order) and thus has evident recommendation as a measure of the concordance between two rankings” and “In general, 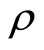 is an easier coefficient to calculation than
is an easier coefficient to calculation than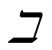 . We shall see... that from most theoretical points of view
. We shall see... that from most theoretical points of view 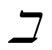 is preferable to
is preferable to )”. It should be noted that Kendall uses
)”. It should be noted that Kendall uses 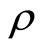 to represent Spearman’s rank correlation coefficient and
to represent Spearman’s rank correlation coefficient and  as Kendall Tau correlation coefficient. [11] declared that nowadays the calculation of Kendall’s coefficient posses no problem. Kendall’s coefficient is equivalent to Spearman’s rank coefficient in terms of the underlying assumptions, but they are not identical in magnitude, since their underlying logic and computational formulae are quite different. Similarly, Kendall’s coefficient and spearman’s rank correlation coefficient imply different interpretations. [12,13] examined the use of Pearson’s product moment correlation coefficient and Spearman’s rank correlation coefficient for geographical data (on map data that are spatially correlated).
as Kendall Tau correlation coefficient. [11] declared that nowadays the calculation of Kendall’s coefficient posses no problem. Kendall’s coefficient is equivalent to Spearman’s rank coefficient in terms of the underlying assumptions, but they are not identical in magnitude, since their underlying logic and computational formulae are quite different. Similarly, Kendall’s coefficient and spearman’s rank correlation coefficient imply different interpretations. [12,13] examined the use of Pearson’s product moment correlation coefficient and Spearman’s rank correlation coefficient for geographical data (on map data that are spatially correlated).
Spearman’s rank correlation coefficient is a nonparametric (that is distribution free) rank statistic proposed as a measure of the strength of the association between two variables as compared to Pearson’s product-moment coefficient, that is a parametric statistic. Similarly, [14] clarified that Spearman’s rank correlation is not a measure of the linear relationship between two variables as some statisticians declared. It accesses how well an arbitrary monotonic function can describe the relationship between two variables, without making any assumptions about the frequency distribution of the variables. Unlike Pearson’s product-moment coefficient, it does not require the assumption that the relationship between the variables is linear nor does it require the variables to be measured on interval scales. [14] confirmed that Pearson’s productmoment correlation coefficient (represented with r) was the first formal correlation measure and it is still the most widely used measure of relationship.
The idea of this paper is to use correlation coefficient to determine the level of relationship between the auxiliary and study variables, after which such data will be analysed with double sampling for regression type estimator to know which correlation level significantly contributes to the objective of implementing auxiliary variable. However, having considered all the correlation coefficient measures, this paper will use Pearson’s productmoment correlation coefficient.
2.4. Pearson’s Product—Moment Correlation Coefficient and Its Coefficient of Determination
Pearson first developed the mathematical formula for this important measure in 1985
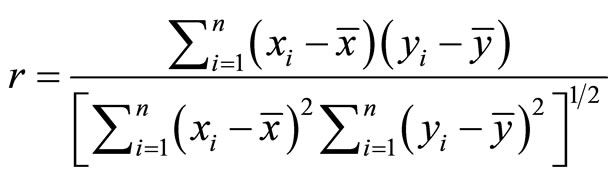 (11)
(11)
[12] presented correlation in Equation (11) as the “function of raw scores and mean”. Equation (11) describes r as the Centred and standardized sum of cross-product of two variables. Using the Cauchy-Schwartz inequality, [15] claim that it can be shown that the absolute value of the numerator is less than or equal to the denominator, therefore,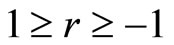 . [14] further presented Pearson Productmoment correlation coefficient as standard covariance. The correlation coefficient is a rescaled covariance and presented as;
. [14] further presented Pearson Productmoment correlation coefficient as standard covariance. The correlation coefficient is a rescaled covariance and presented as;
 (12)
(12)
where
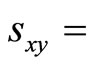 Sample covariance of
Sample covariance of 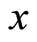 and
and 
 = Sample standard deviation of
= Sample standard deviation of 
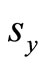 = Sample standard deviation of
= Sample standard deviation of 
When the covariance is divided by two standard deviations, the range of the covariance is rescaled to the interval between −1 and +1, thus the interpretation of correlation follows as in the case of Equation (11).
Correlation is sometimes criticized as having no clinical interpretation or meaning [16]. This criticism is mitigated by taking the square of the correlation coefficient which is often called COEFFICIENT OF DETERMINATION. [17] expressed coefficient of determination 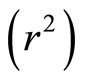 proportion of common variation in the two variables (that is the “strength” or “magnitude” of the relationship). He emphasized that it is important to know this magnitude or strength in order to evaluate the correlation between variables. The square index is interpreted as proportion of variation in one variable accounted for by differences in the other variable. According to [16],
proportion of common variation in the two variables (that is the “strength” or “magnitude” of the relationship). He emphasized that it is important to know this magnitude or strength in order to evaluate the correlation between variables. The square index is interpreted as proportion of variation in one variable accounted for by differences in the other variable. According to [16],
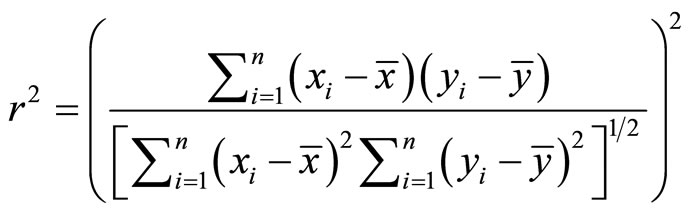 (13)
(13)
Or
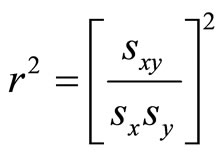 (14)
(14)
where 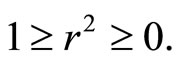
Error and Interpretation in Correlation Coefficient
Most common error associated with correlation and regression analysis, as emphasized by [16], is confusing when interpreting correlation coefficient result. The most common error in correlation coefficient interpretation is to conclude that changes in one variable causes changes in the other. Correlation coefficient indicates that characteristics vary together or in opposite direction. However, not interpreting the results of Correlation coefficient is another common error. [16] claims that the coefficient must be interpreted in light of the relationship under study and [18] has given different ways to interpret and estimate for coefficient of determination, though based on theory dependent.
For the purpose of this investigation, this article will make use of the interpretation criteria established by [19] (as seen in Table 1) but with boundary amendment (as in Table 2).
3. Comparison of Estimators
This section proposes on how the empirical comparison will be executed. Minimum variance, coefficient of variation and relative efficiency are the statistical measures that will be used to compare the estimated variance and
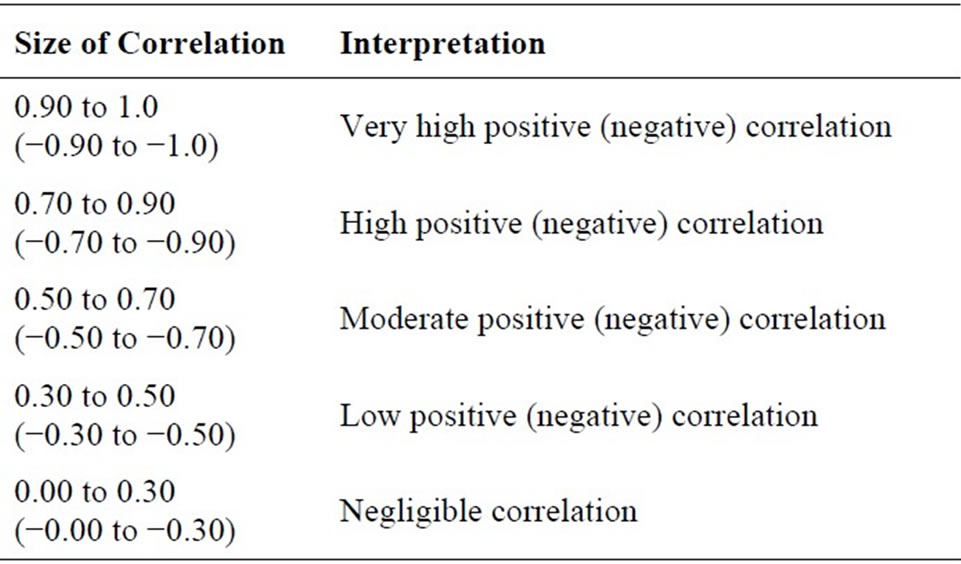
Table 1. Correlation coefficient interpretation as presented by [19].

Table 2. Correlation coefficient interpretation proposed for this investigation.
the standard deviation of double sampling for regression type estimator at three levels of correlation coefficient which will be termed as high, moderate and low positive linear correlation coefficients (see Table 2 for the details on the correlation coefficient).
3.1. Coefficient of Variation (CV)
Coefficient of variation is a statistical measure that will be used to know the level of variability in each of these levels of correlation coefficients. [2] defines the coefficient of variation of an estimator  as the measure of relative variability. Mathematically, it is presented as;
as the measure of relative variability. Mathematically, it is presented as;
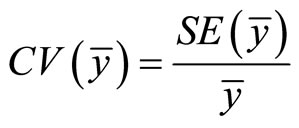 (15)
(15)
where  = Sample mean;
= Sample mean; 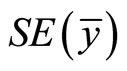 = Standard Error of the estimator
= Standard Error of the estimator ; and
; and 
The estimated Coefficient of Variation is the standard error expressed as a percentage of the mean.
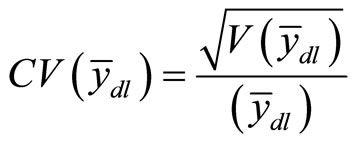 (16)
(16)
This can also be presented as;
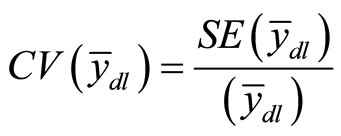 (17)
(17)
In this article, Equation (16) will be used for the computation of the coefficient of variation at different levels of the correlation coefficient after which a tabular comparison will be made.
3.2. Relative Efficiency
Relative Efficiency is another statistical measure that will be used to measure the efficiency of one estimator over another. The relative efficiency of estimator “a” to estimator “b” is expressed as;
 (18)
(18)
3.2.1. Relative Efficiency of High Positive Linear Correlation to Medium Positive Linear Correlation
This measures the efficiency of double sampling for regression estimator with high positive linear correlation coefficient to double sampling for regression estimator with medium positive linear correlation coefficient. This is presented as:
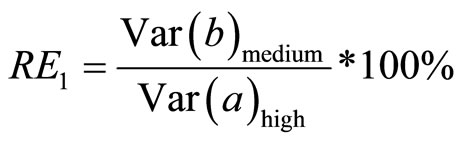 (19)
(19)
3.2.2. Relative Efficiency of High Positive Linear Correlation to Low Positive Linear Correlation
This measures the efficiency of double sampling for regression estimator with high positive linear correlation coefficient to double sampling for regression estimator with low positive linear correlation coefficient. This is presented as:
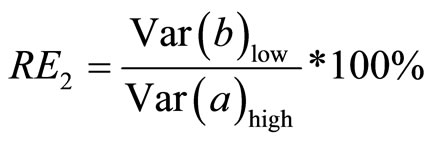 (20)
(20)
3.2.3. Relative Efficiency of High Positive Linear Correlation to Low Positive Linear Correlation
This measures the efficiency of double sampling for regression estimator with high positive linear correlation coefficient to double sampling for regression estimator with low positive linear correlation coefficient. This is presented as:
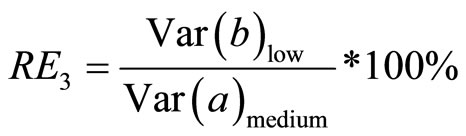 (21)
(21)
4. Empirical Comparison
This research work uses primary data obtained from five hundred and seventy four (574) questionnaires distributed to the staff and students of Nursing school, Perioperative Nursing School, School of mid-wifery and Occupational Health School, all in University College Hospital (UCH) in Oyo state of Nigeria. The double sampling uses the household monthly average expenditure (in thousands of Naira) on food consumption as the study variable 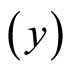 and the household size as the auxiliary variable
and the household size as the auxiliary variable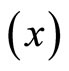 . The double sampling obtains the first and second sample sizes at five different levels as presented below.
. The double sampling obtains the first and second sample sizes at five different levels as presented below. 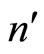 is the sample size at first phase and
is the sample size at first phase and 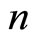 is the sample size at the second phase.
is the sample size at the second phase.
It will be observed in Table 3 that the minimum proportion is obtained at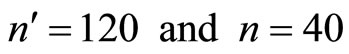 . Hence,
. Hence,  are the optimum sample sizes for the first and second phases respectively. This investigation will obtain all requirements at this optimum sample sizes.
are the optimum sample sizes for the first and second phases respectively. This investigation will obtain all requirements at this optimum sample sizes.

Table 3. Summary of the first and second phase sample sizes at different levels.
4.1. At High Positive Correlation
Where there exists high positive correlation, Figure 1 shows the existence of positive linear relationship between the auxiliary and the study variables at 
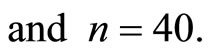 SPSS software was used to perform simple linear regression analysis on the data, the model obtained is presented in Equation (22) below.
SPSS software was used to perform simple linear regression analysis on the data, the model obtained is presented in Equation (22) below.
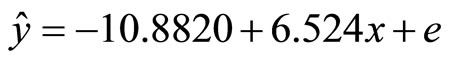 (22)
(22)
And the Pearson’s Product-moment Correlation Coefficient is obtained as 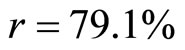 and the Coefficient of determination is obtained as
and the Coefficient of determination is obtained as . From Equation 22 and Figure 1, this means that the intercept on
. From Equation 22 and Figure 1, this means that the intercept on 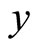 axis is not zero; hence, these data are suitable for double sampling for regression type estimation. Similarly, the result of the correlation coefficient shows that
axis is not zero; hence, these data are suitable for double sampling for regression type estimation. Similarly, the result of the correlation coefficient shows that 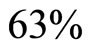 of the variation in the household expenditure
of the variation in the household expenditure 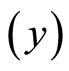 is explained by the household size
is explained by the household size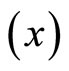 .
. ,
,  ,
, 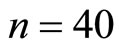 ,
, 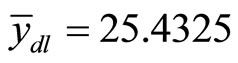 ,
,  ,
,  ,
, 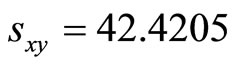 ,
,  and
and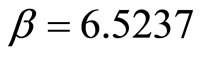 .
.
Using Equation (8),  and the corresponding standard error is
and the corresponding standard error is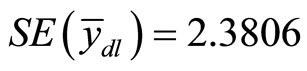 .
.
4.2. At Medium Positive Correlation
Where there exists medium positive correlation, Figure 2 shows the existence of approximately positive linear relationship between the auxiliary and the study variables at  and
and . SPSS software was used to perform simple linear regression analysis on the data, the model obtained is presented in Equation (23) below.
. SPSS software was used to perform simple linear regression analysis on the data, the model obtained is presented in Equation (23) below.
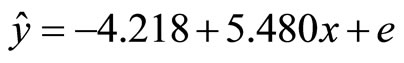 (23)
(23)
And the Pearson’s Product-moment Correlation Coefficient is obtained as 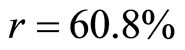 and the Coefficient of determination is obtained as
and the Coefficient of determination is obtained as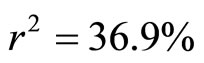 . From Equation (23) and Figure 2, this means that the intercept on
. From Equation (23) and Figure 2, this means that the intercept on 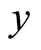 axis is not zero, hence, these data are suitable for double sampling for regression type estimation. Similarly, the result of the correlation coefficient shows that of the variation in the household expenditure
axis is not zero, hence, these data are suitable for double sampling for regression type estimation. Similarly, the result of the correlation coefficient shows that of the variation in the household expenditure 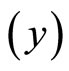 is explained by the household size
is explained by the household size .
. ,
,  ,
,
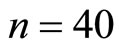 ,
,  ,
,  ,
, 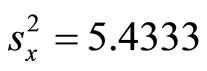 ,
,
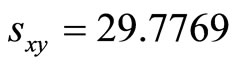 ,
,  and
and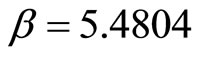 . Using
. Using
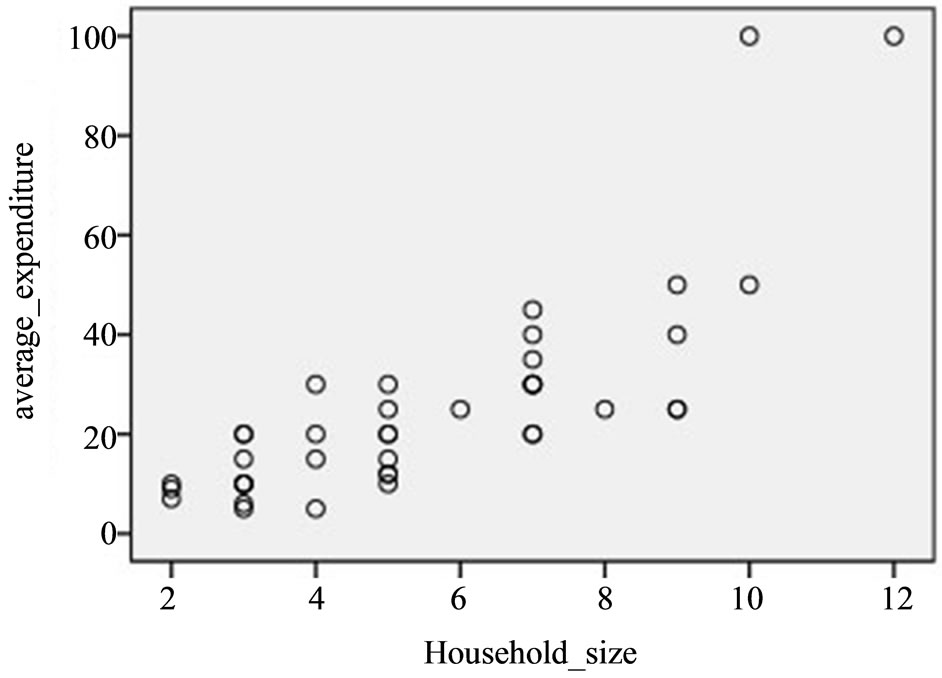
Figure 1. Scatter plot of y against x at high correlation level.

Figure 2. Scatter plot of y against x at high correlation level.
Equation (8), 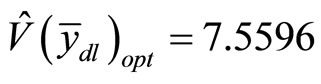 and the corresponding standard error is
and the corresponding standard error is 
4.3. At Low Positive Correlation
Where there exists medium positive correlation, Figure 3 below shows the existence of approximately positive linear relationship between the auxiliary and the study variables at 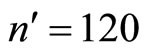 and
and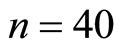 . SPSS software was used to perform simple linear regression analysis on the data, the model obtained is presented in Equation (24) below.
. SPSS software was used to perform simple linear regression analysis on the data, the model obtained is presented in Equation (24) below.
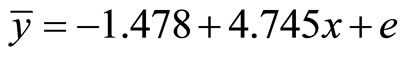 (24)
(24)
And the Pearson’s Product-moment Correlation Coefficient is obtained as 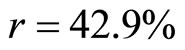 and the Coefficient of determination is obtained as
and the Coefficient of determination is obtained as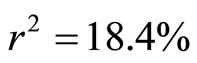 . From Equation (24) and Figure 3, this means that the intercept on
. From Equation (24) and Figure 3, this means that the intercept on 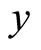 axis is not zero, hence, these data are suitable for double sampling for regression type estimation. Similarly, the result of the correlation coefficient shows that of the variation in the household expenditure
axis is not zero, hence, these data are suitable for double sampling for regression type estimation. Similarly, the result of the correlation coefficient shows that of the variation in the household expenditure 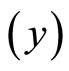 is explained by the household size
is explained by the household size .
. ,
, 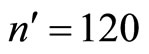 ,
,
 ,
,  ,
,  ,
, 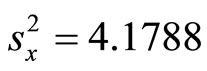 ,
,
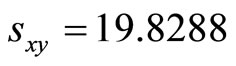 ,
, 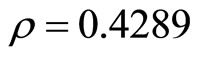 and
and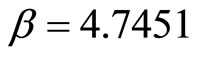 . Using Equation (8),
. Using Equation (8), 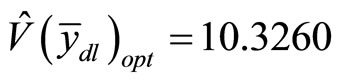 and the corresponding standard error is
and the corresponding standard error is 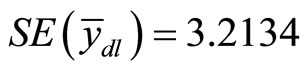
Summary of the various computations at the three correlation levels is presented in Table 4.
4.4. Computation of the Coefficient of Variation
As proposed in Equation (17), the coefficient of variation for each correlation coefficient level is obtained and interpreted in Table 5.
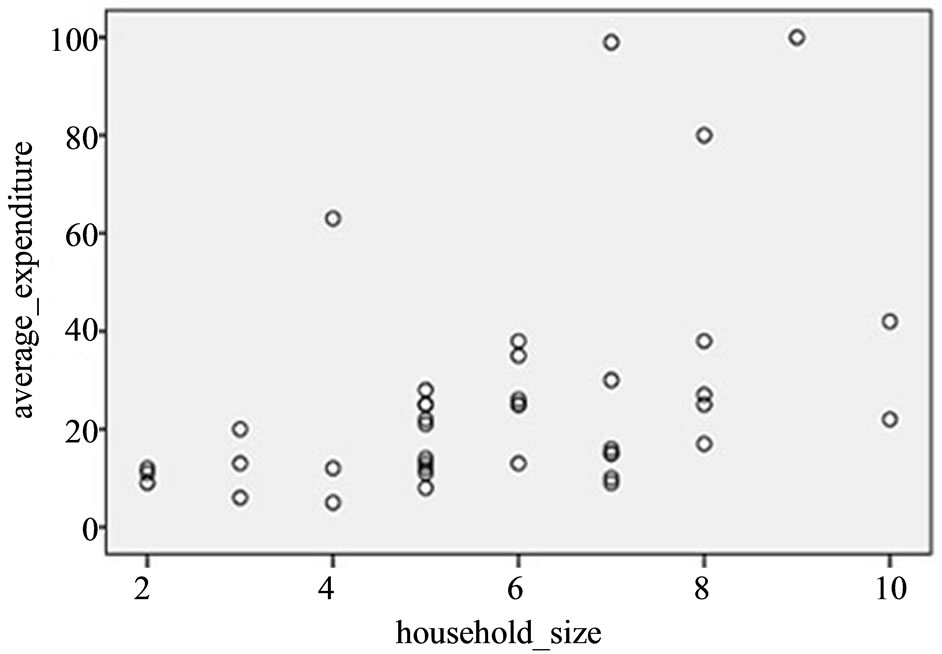
Figure 3. Scatter plot of y against x at low correlation level.
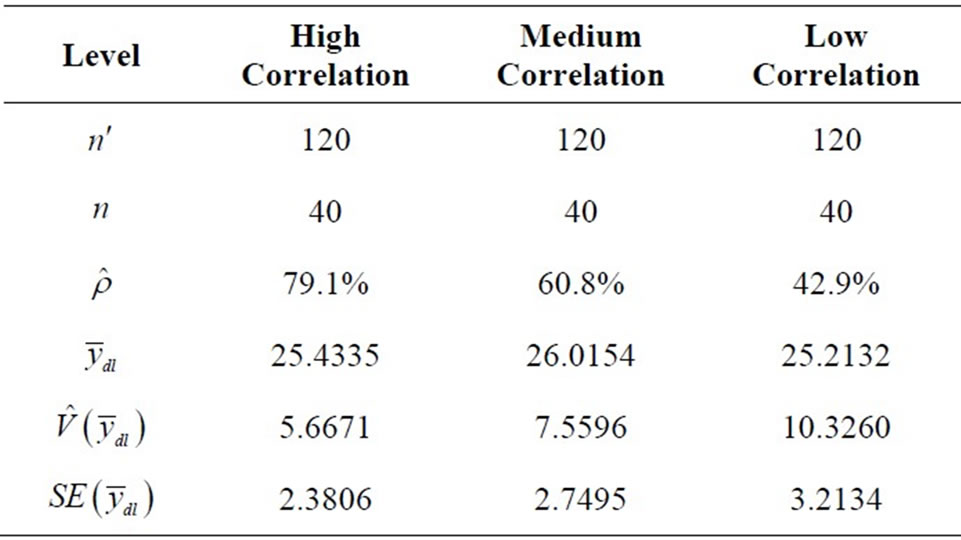
Table 4. Summary of the different estimated variances at three different correlation levels.

Table 5. Summary of the different estimated variances at three different correlation levels.
4.5. Computation of the Relative Efficiency
4.5.1. Relative Efficiency of High Positive Linear Correlation Coefficient to Medium Positive Linear Correlation Coefficient
Using Equation (19):
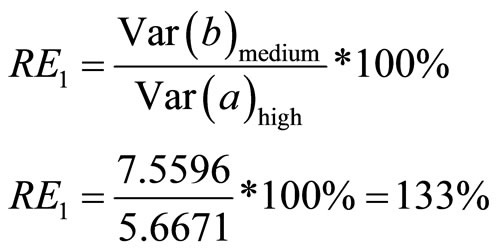 (25)
(25)
4.5.2. Relative Efficiency of High Positive Linear Correlation Coefficient to Low Positive Linear Correlation Coefficient
Using Equation (19):
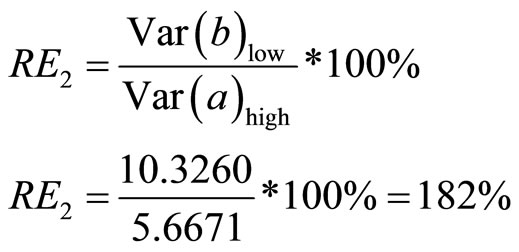 (26)
(26)
4.5.3. Relative Efficiency of Medium Positive Linear Correlation Coefficient to Low Positive Linear Correlation Coefficient
Using Equation (19):
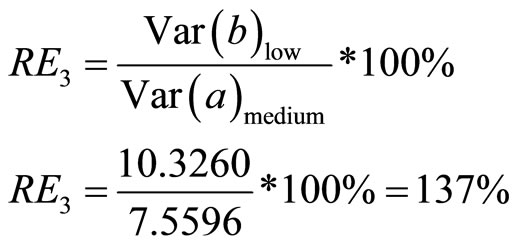 (27)
(27)
The result obtained for the relative efficiency as derived in Equations (25)-(27) are tabulated as seen in Table 6.
5. Conclusion
This paper examines the effect of correlation level on the use of auxiliary variable in double sampling for regression estimation. The findings revealed that double sampling for regression with high correlation coefficient (between the auxiliary and study variables) has the minimum variance 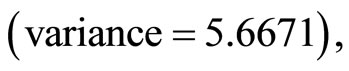 hence, is the most efficient estimator. Double sampling for regression with medium correlation coefficient performs better
hence, is the most efficient estimator. Double sampling for regression with medium correlation coefficient performs better 
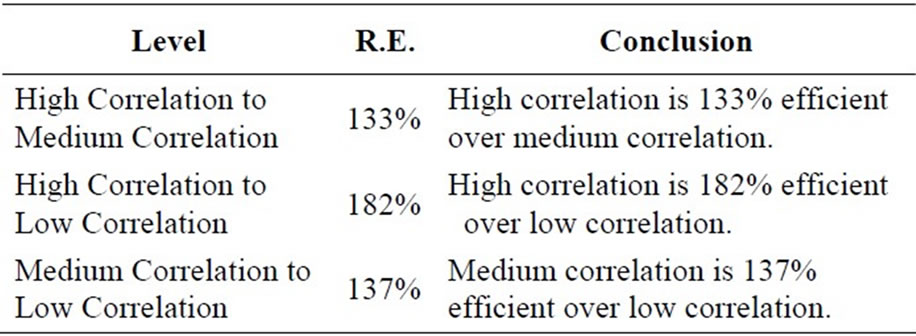
Table 6. Summary of the computed relative efficiency.
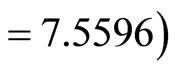 ; while least efficient estimator is double sampling for regression with low correlation level
; while least efficient estimator is double sampling for regression with low correlation level 
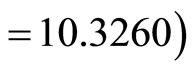 . Thus, the higher the correlation coefficient (between the auxiliary and the study variables) is, the smaller the variance (as seen in Table 4) is. Similarly, it was discovered that double sampling for regression with high correlation coefficient has the highest precision
. Thus, the higher the correlation coefficient (between the auxiliary and the study variables) is, the smaller the variance (as seen in Table 4) is. Similarly, it was discovered that double sampling for regression with high correlation coefficient has the highest precision ; with double sampling for regression with medium correlation coefficient having higher precision
; with double sampling for regression with medium correlation coefficient having higher precision 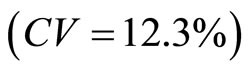 and finally is double sampling for regression with low correlation coefficient having least precision
and finally is double sampling for regression with low correlation coefficient having least precision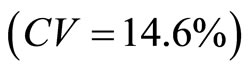 . Hence, the higher the correlation coefficient (between the auxiliary and the study variables) is, the higher the precision of the estimate (as revealed in Table 5) is. Finally, Table 6 revealed the relative efficiency of double sampling for regression with high correlation coefficient over double sampling for regression with medium correlation coefficient. Similarly, it is the relative efficiency of double sampling for regression with high correlation coefficient over double sampling for regression with low correlation coefficient. Hence, the higher the correlation coefficient (between the auxiliary and the study variables) is, the more efficient the estimator is.
. Hence, the higher the correlation coefficient (between the auxiliary and the study variables) is, the higher the precision of the estimate (as revealed in Table 5) is. Finally, Table 6 revealed the relative efficiency of double sampling for regression with high correlation coefficient over double sampling for regression with medium correlation coefficient. Similarly, it is the relative efficiency of double sampling for regression with high correlation coefficient over double sampling for regression with low correlation coefficient. Hence, the higher the correlation coefficient (between the auxiliary and the study variables) is, the more efficient the estimator is.
Although, auxiliary information in double sampling procedure increases the precision of an estimate, this paper, therefore, suggested for researchers to know that the correlation level between the study variable and the auxiliary variable will contribute to the efficiency of the estimator under study. In addition, this result can be generalised to all sample survey methodologies that use auxiliary variable to increase the precision of the estimator.
REFERENCES
- W. G. Cochran, “Sampling Technique,” 3rd Edition, John Willey and Sons Inc., New York, 1977.
- L. S. Lohr, “Sampling Design and Analysis,” 2nd Edition, Brooks/Cole Cengage Learning, 2010, p. 596.
- F. C. Okafor and H. Lee, “Double Sampling for Ratio and Regression Estimation with Sub-Sampling the Non-Respondents,” Survey Methodology, Vol. 26, No. 2, 2000, pp. 183-188.
- B. K. Pradhan, “A Chain Regression Estimator in TwoPahse Sampling Using Multi-Auxiliary Information,” Bulletin of the Malaysian Mathematical Sciences Society, Vol. 28, No. 1, 2005, pp. 81-86.
- A. A. Sodipo and K. O. Obisesan, “Estimation of the Population Mean Using Difference Cum Ratio Estimator with Full Response on the Auxiliary Character,” Research Journal of Applied Sciences, Vol. 2, No. 6, 2007, pp. 769- 772.
- P. Mukhopadhyay, “Survey Sampling,” Narosa Publishing House Pvt. Ltd., 2007, p. 256.
- F. C. Okafor, “Sample Survey Theory with Applications,” Afro-Orbis Publication Ltd., 2002.
- A. Koutsoyiannis, “Theory of Econometrics,” 2nd Edition, Palgrave Publishers Ltd. (Formerly Macmillan Press Ltd.), 1977.
- M. G. Kendall, “A New Measure of Rank Correlation,” Biometrika, Vol. 30, No. 1, 1938, pp. 81-89.
- M. G. Kendall, “Rank Correlation Methods,” 4th Edition, Griffin, London, 1948.
- T. Kossowski and J. Kauke, “Comparison of Values of Pearson’s and Spearman’s Correlation Coefficients on the Same Set of Data,” Quaestiones Geographicae, Vol. 30, No. 2, 2011, pp. 87-93.
- R. Haining, “Bivariate Correlation with Spatial Data,” Geographical Analysis, Vol. 23, No. 3, 1991, pp. 210-227. http://dx.doi.org/10.1111/j.1538-4632.1991.tb00235.x
- D. A. Griffith, “Spatial Autocorrelation and Sptial Filtering” Springer, Berlin, 2003. http://dx.doi.org/10.1007/978-3-540-24806-4
- W. A. Nicewander and J. L. Rodgers, “Thirteen Ways to Look at Correlation Coefficient,” The American Statistician, Vol. 42, No. 1, 1988, pp. 59-66.
- F. M. Lord and M. R. Novick, “Statistical Theories of Mental Test Scores,” Addison-Wesley, Reading, 1968.
- M. A. Lang Tom, “Common Statistical Errors Even You Can Find! Part 4: Errors in Correlation and Regression Analyses,” AMWA Journal, Vol. 20, No. 1, 2005, pp. 10- 11.
- N. Shaban, “Analysis of Correlation and Regression Coefficients of the Interaction between Yildans Come Parameters of Snap Bears Plants,” Trakia Journal of Science, Vol. 3, No. 6, 2005, pp. 27-31.
- D. J. Ozer, “Correlation and Coefficient of Determination,” Psychological Bullentin, Vol. 97, No. 2, 1985, pp. 307- 315. http://dx.doi.org/10.1037/0033-2909.97.2.307
- M. M. Mukaka, “A Guide to Appropriate Use of Correlation Coefficient in Medical Research,” MMJ, Vol. 24, No. 3, 2012, pp. 69-71.
NOTES
*Corresponding author.

