Open Journal of Statistics
Vol.3 No.4(2013), Article ID:35930,13 pages DOI:10.4236/ojs.2013.34028
Shrinkage Testimator in Gamma Type-II Censored Data under LINEX Loss Function
Department of statistics, Payame Nour University of Tehran, 19395-4697, Iran
Email: ali_shadrokh@pnu.ac.ir, pazira.b@gmail.com
Copyright © 2013 Ali Shadrokh, Hassan Pazira. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received September 1, 2012; revised January 1, 2013; accepted January 18, 2013
Keywords: Gamma distribution; Shrinkage estimator and factor; Asymmetric loss function; Level of significance; Testimation; Monte-Carlo simulation
ABSTRACT
Prakash and Singh presented the shrinkage testimators under the invariant version of LINEX loss function for the scale parameter of an exponential distribution in presence Type-II censored data. In this paper, we extend this approach to gamma distribution, as Prakash and Singh’s paper is a special case of this paper. In fact, some shrinkage testimators for the scale parameter of a gamma distribution, when Type-II censored data are available, have been suggested under the LINEX loss function assuming the shape parameter is to be known. The comparisons of the proposed testimators have been made with improved estimator. All these estimators are compared empirically using Monte Carlo simulation.
1. Introduction
In life-testing research, the most widely used life distribution is the Gamma with probability density function for any random variable x;
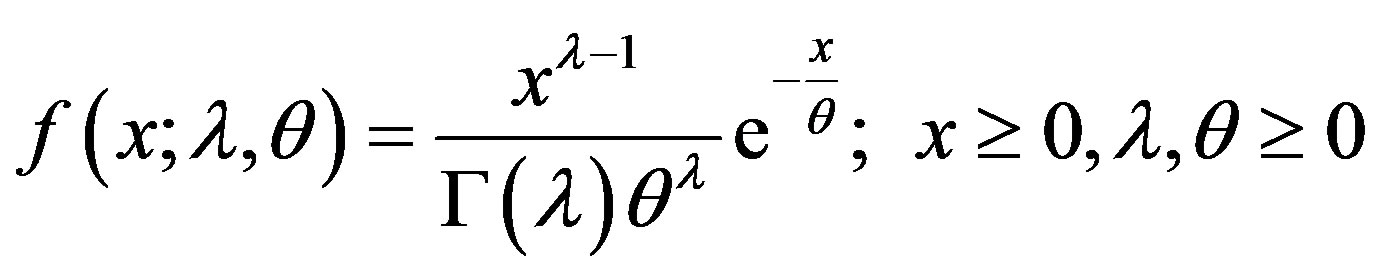 . (1.1)
. (1.1)
Let  be the random samples of size n taken form the Gamma distribution. The parameter
be the random samples of size n taken form the Gamma distribution. The parameter  and
and  are called the shape and scale parameter, respectively. It is crucial to have in-depth study of the (Classic and Bayes) estimate of the scale parameter of Gamma distribution because, in several cases, the distribution of the minimal sufficient statistics is Gamma (see Parsian and Kirmani [1]). Pazira and Shadrokh [2] derived Bayes estimators of the scale parameter of gamma distribution on the two asymmetric loss function LINEX and Precautionary by using several prior distributions and then compared the efficiency of all estimates. In the present paper, concentration is on the gamma distribution.
are called the shape and scale parameter, respectively. It is crucial to have in-depth study of the (Classic and Bayes) estimate of the scale parameter of Gamma distribution because, in several cases, the distribution of the minimal sufficient statistics is Gamma (see Parsian and Kirmani [1]). Pazira and Shadrokh [2] derived Bayes estimators of the scale parameter of gamma distribution on the two asymmetric loss function LINEX and Precautionary by using several prior distributions and then compared the efficiency of all estimates. In the present paper, concentration is on the gamma distribution.
Ferguson [3], Zellner and Geisel [4], Aitchison and Dunsmore [5], Varian [6], and Berger [7] indicated to insufficient to symmetric loss function and just Varian [6] suggested asymmetric linear loss function. This loss function was widely used by several authors; among of them were Basu and Ebrahimi [8], Pandey [9], Soliman [10], and Prakash and Singh [11]. Following Basu and Ebrahimi [8], the invariant form of the LINEX loss function (ILL) for any parameter  is defined as
is defined as
 , (1.2)
, (1.2)
where c is the shape parameter and  is any estimate of the parameter
is any estimate of the parameter .
.
The LINEX loss function is convex and the shape of this loss function is determined by the value of c. The negative (positive) value of c gives more weight to overestimation (underestimation) and its magnitude reflects the degree of asymmetry. It is seen that, for c = 1, the function is quite asymmetric with overestimation being costlier than underestimation. If c < 0, it rises almost exponentially when the estimation error 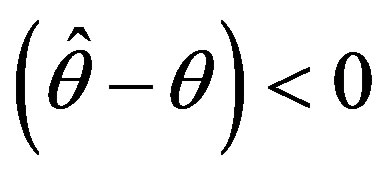 and almost linearly when
and almost linearly when . For small values of |c|, the LINEX loss function is almost symmetric and not far from squared error loss function.
. For small values of |c|, the LINEX loss function is almost symmetric and not far from squared error loss function.
Pandey [9], Parsian and Farsipour [12], Singh, Gupta, and Upadhyay [13], Misra and Meulen [14], Ahmadi, Doostparast, and Parsian [15], Xiao, Takada, and Shi [16], Singh, Prakash, and Singh [17] and others have used the LINEX loss function in the various estimation and prediction problems.
In life-testing, fatigue failures and other kinds of destructive test situations, the observations usually occurred in an ordered manner such a way that the weakest items failed first and then the second one and so on. Let us suppose that n items are put on life test and terminate the experiment when r (< n) items have failed. If  denote the first r observations having a common density function as given in (1.1) then the joint probability density function is given by
denote the first r observations having a common density function as given in (1.1) then the joint probability density function is given by
 (1.3)
(1.3)
where
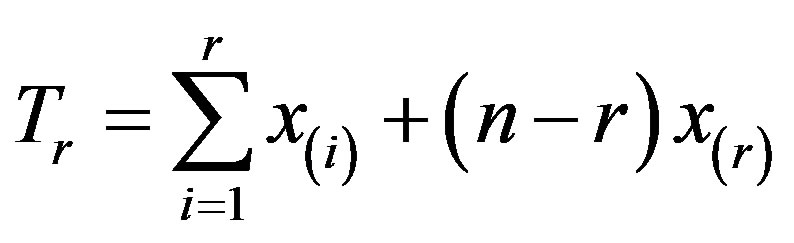 (1.4)
(1.4)
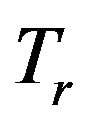 is a complete sufficient statistic of
is a complete sufficient statistic of 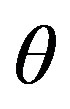 and distributed as gamma distribution with parameters
and distributed as gamma distribution with parameters . The maximum likelihood estimator (MLE) of
. The maximum likelihood estimator (MLE) of  is given by
is given by
 (1.5)
(1.5)
and can easily show that 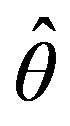 is the minimum variance unbiased estimator (MVUE) of
is the minimum variance unbiased estimator (MVUE) of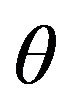 .
.
Roa and Srivastava [18] considered a class for the total test time as
 and found the value of the constant
and found the value of the constant
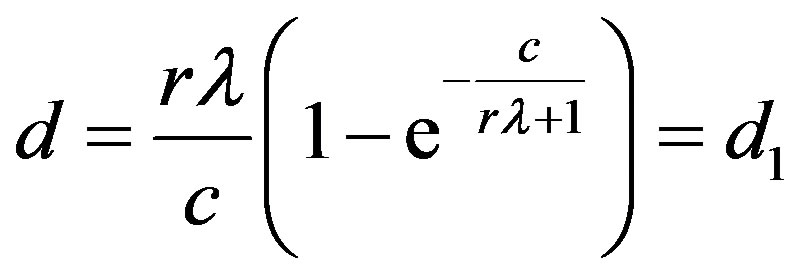
(say) which minimizes the risk of Y under the ILL. The minimum risk estimator is
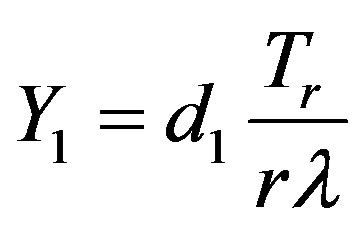
with the minimum risk under ILL
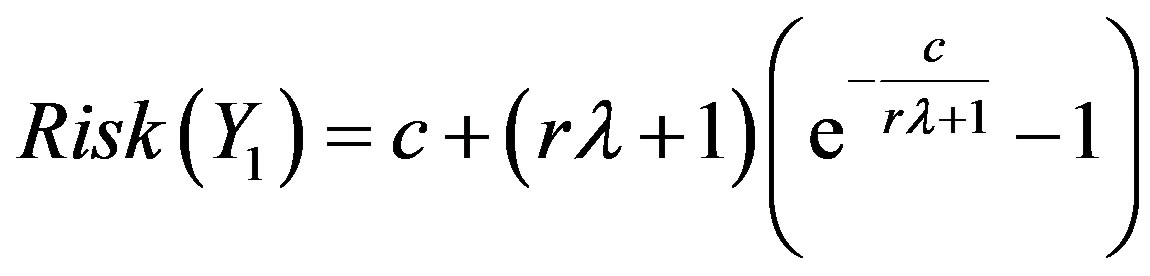 , (1.6)
, (1.6)
for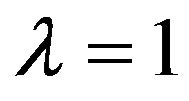 , see Prakash and Singh [11].
, see Prakash and Singh [11].
In the present paper, some shrinkage testimators for the scale parameter of a gamma distribution, when Type-II censored data are available, have been suggested under the ILL loss function assuming the shape parameter is to be known.
2. Shrinkage Testimators and their Properties
Following Thompson [19], the shrinkage estimator for the parameter  is given by
is given by
 . (2.1)
. (2.1)
The value of the shrinkage factor  near to the zero implies strong belief in the guess value
near to the zero implies strong belief in the guess value 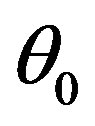 and near to one implies a strong belief in the sample values. Several researchers have studied the performance of the shrinkage estimators and found that the shrinkage estimator performs better with respect to any usual estimator when the guess value
and near to one implies a strong belief in the sample values. Several researchers have studied the performance of the shrinkage estimators and found that the shrinkage estimator performs better with respect to any usual estimator when the guess value  is close to the parameter
is close to the parameter . This suggests that we may test the hypothesis
. This suggests that we may test the hypothesis 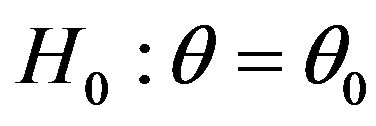 against
against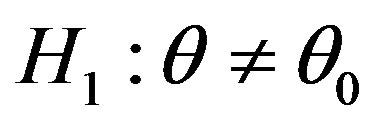 . A test statistic
. A test statistic

is available for testing the hypothesis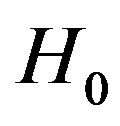 .
.
The loss for estimator  under the ILL is defined as
under the ILL is defined as

where

and
 .
.
The risk of the proposed shrinkage estimator 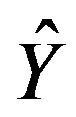 under the ILL is given by
under the ILL is given by
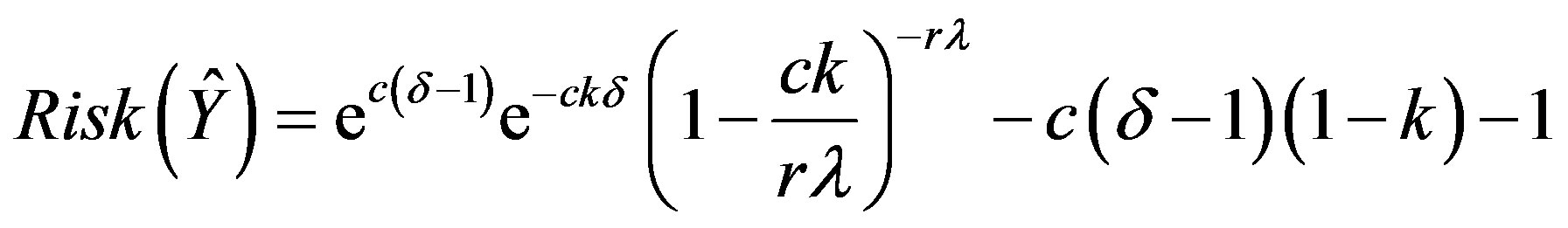 (2.2)
(2.2)
The value of 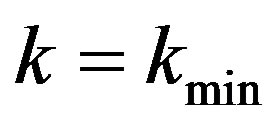 (say), which minimizes the risk
(say), which minimizes the risk 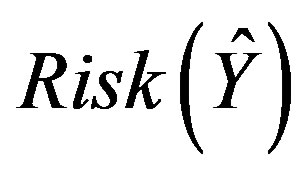 is thus obtained by solving the given equation
is thus obtained by solving the given equation
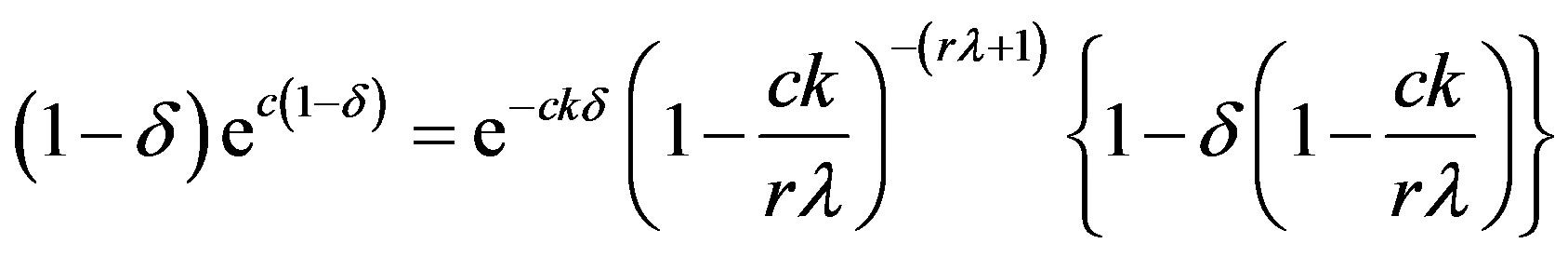 . (2.3)
. (2.3)
The value of 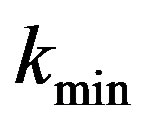 depends upon the unknown parameter
depends upon the unknown parameter . Hence, an estimate
. Hence, an estimate 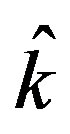 of
of 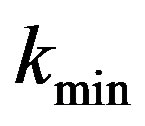 is obtained by replacing the parameter
is obtained by replacing the parameter  to its minimum variance unbiased estimator. Based on this, the proposed shrinkage testimator for the scale parameter
to its minimum variance unbiased estimator. Based on this, the proposed shrinkage testimator for the scale parameter  is defined as
is defined as
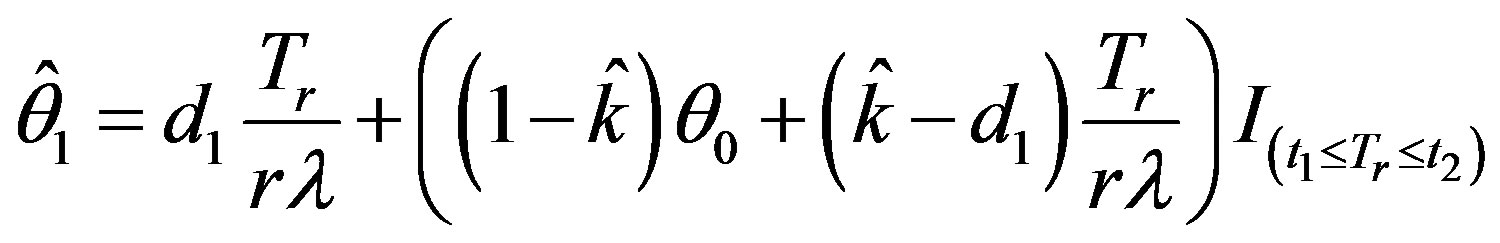 , (2.4)
, (2.4)
where 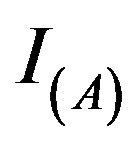 denotes the indicator of A,
denotes the indicator of A, 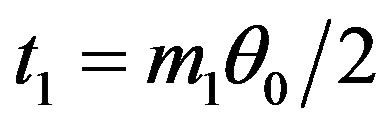 and
and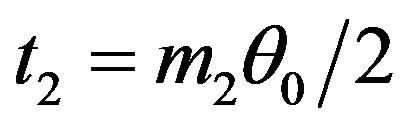 . Here
. Here 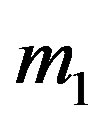 and
and 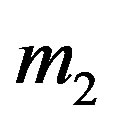 are the values of the lower and upper
are the values of the lower and upper
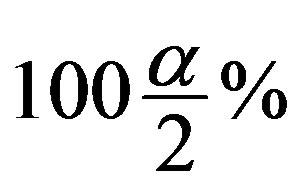
points of the chi-square distribution with  degrees of freedom. The risk under the ILL for the shrinkage testimator
degrees of freedom. The risk under the ILL for the shrinkage testimator 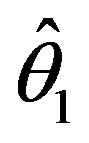 is given by
is given by
 , (2.5)
, (2.5)
where
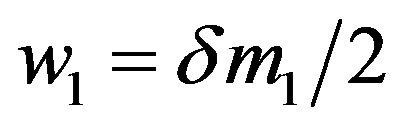 ,
, 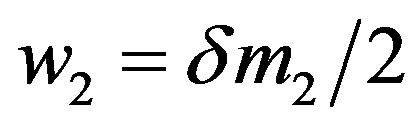 ,
,  ,
, 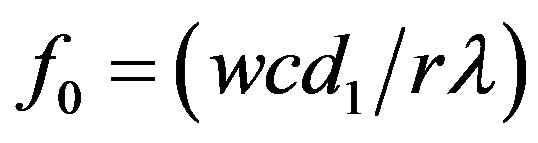 ,
, 
and  may be a function of
may be a function of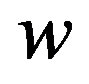 . For
. For , see Prakash and Singh [11].
, see Prakash and Singh [11].
Waikar, Schuurmann, and Raghunathan [20] has suggested an idea of selecting the shrinkage factor which is the function of the test statistic i.e., under 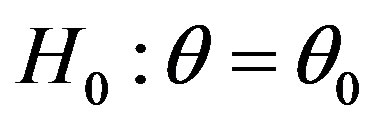
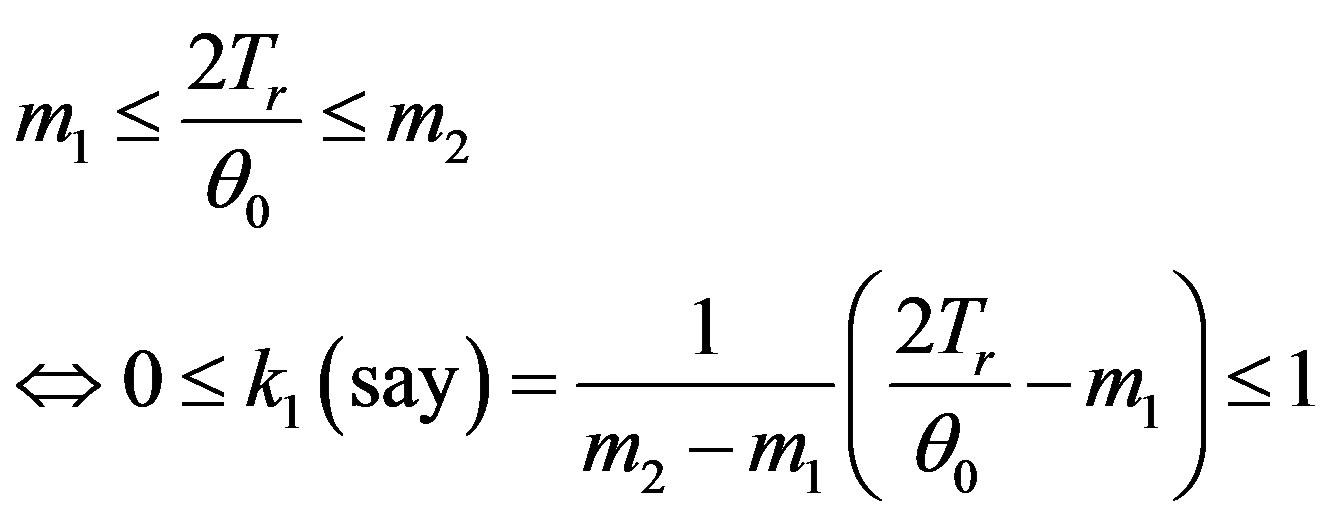 .
.
Therefore, the proposed shrinkage testimator based on 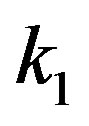 is given by
is given by
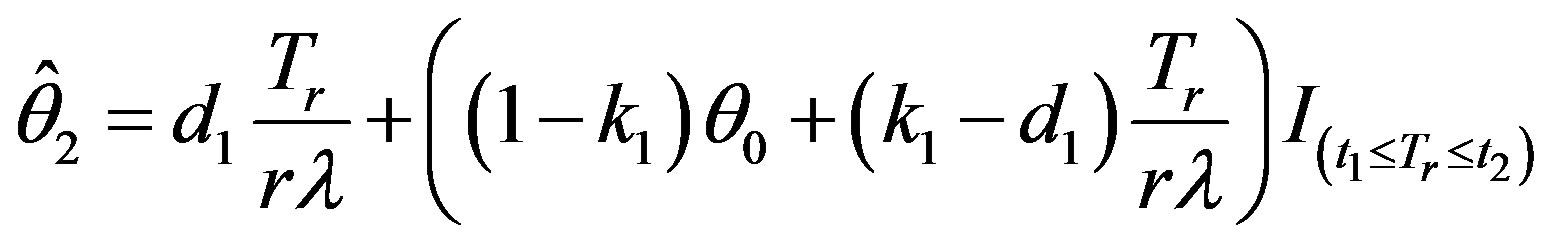 . (2.6)
. (2.6)
The risk under the ILL for the shrinkage testimator 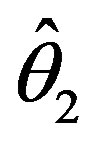 is given by
is given by
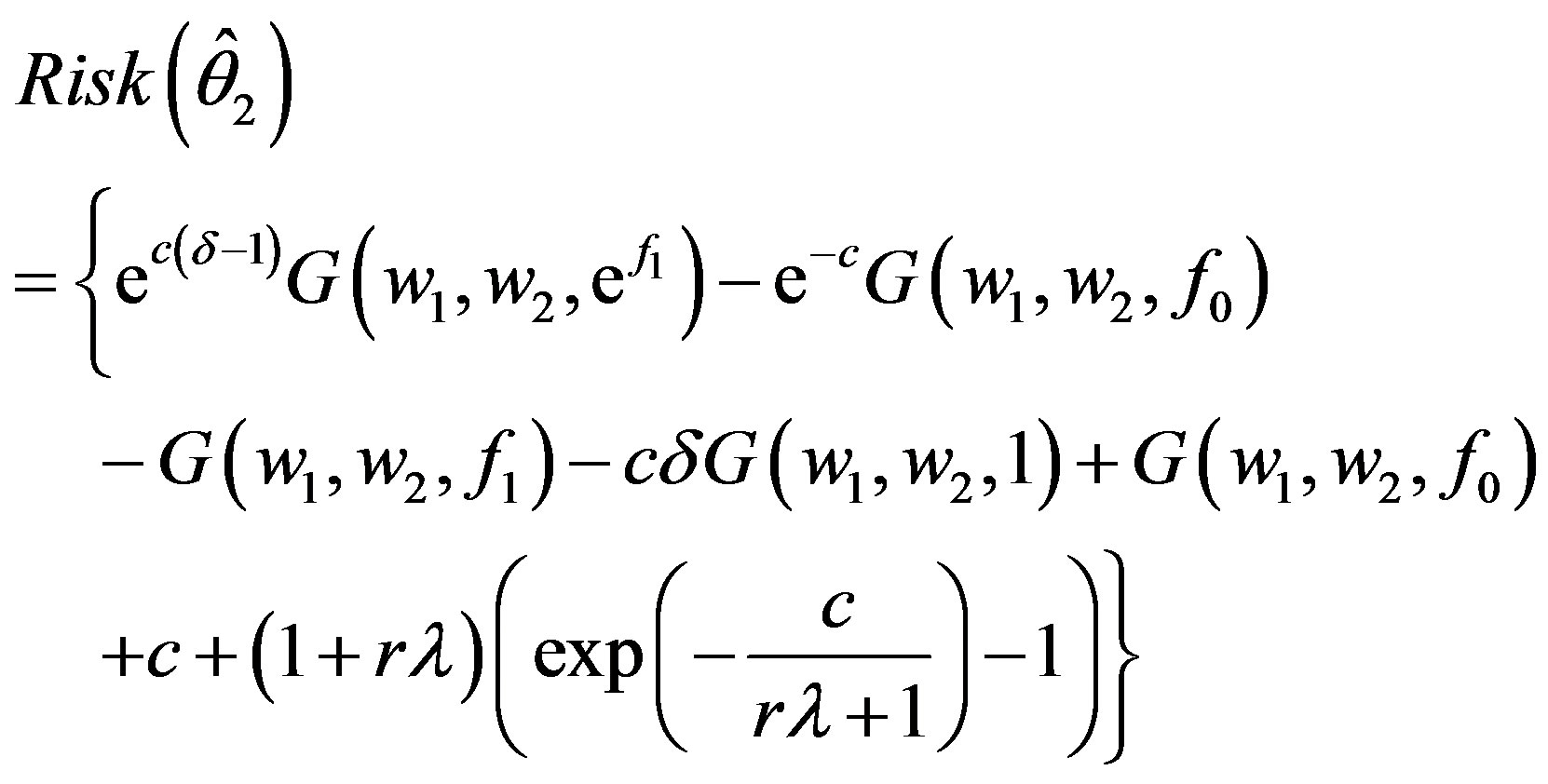 , (2.7)
, (2.7)
where
 .
.
For , see Prakash and Singh [11].
, see Prakash and Singh [11].
When 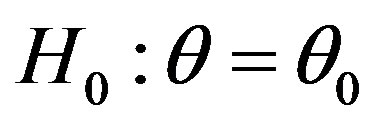 is accepted,
is accepted,
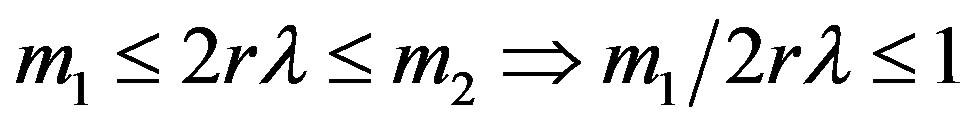 .
.
If one is interested in taking smaller values of the shrinkage factor, he can take . The proposed shrinkage testimator is
. The proposed shrinkage testimator is
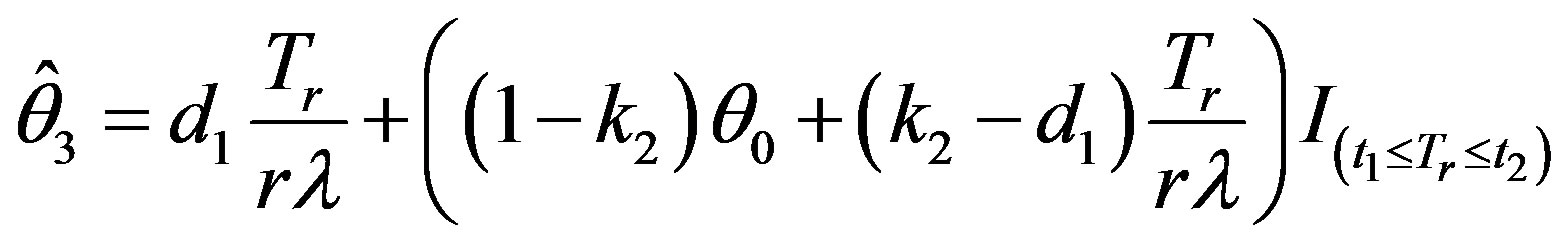 (2.8)
(2.8)
where
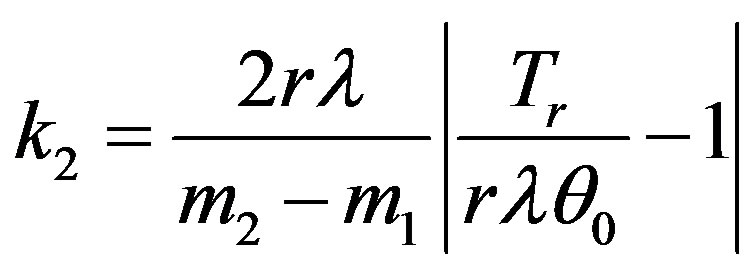 ;
;
it may be possible that the value of shrinkage factor is negative so positive is taken. Adke, Waikar, and Schuurmann [21] and Pandey, Malik, and Srivastava [22] have considered this type of shrinkage factor. The risk of the shrinkage testimator  is given by
is given by
 , (2.9)
, (2.9)
where
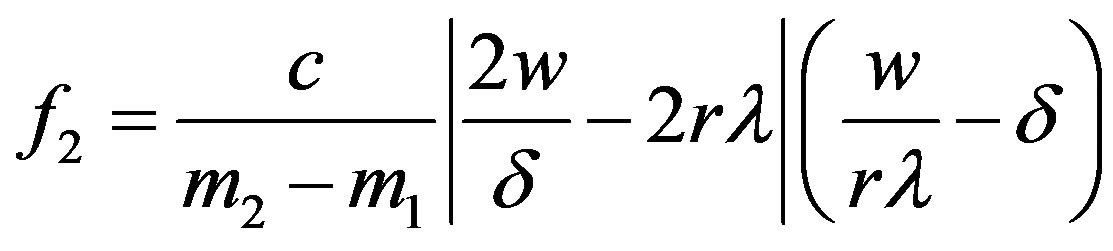 .
.
For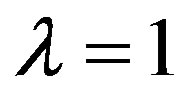 , see Prakash and Singh [11].
, see Prakash and Singh [11].
The minimum value of constant ,
, 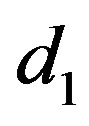 obtained for the class
obtained for the class , lies between zero and one. Hence, it may be a choice for the shrinkage factor. Thus, the proposed shrinkage testimator may be considered as
, lies between zero and one. Hence, it may be a choice for the shrinkage factor. Thus, the proposed shrinkage testimator may be considered as
 (2.10)
(2.10)
The risk of the proposed shrinkage testimator  under ILL is given by
under ILL is given by
 , (2.11)
, (2.11)
where
 .
.
For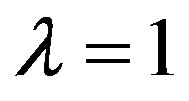 , see Prakash and Singh [11].
, see Prakash and Singh [11].
3. Numerical Illustration
The relative efficiency for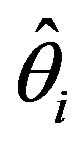 ;
;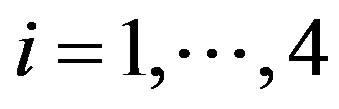 , with respect to the minimum risk improved estimator under the ILL is defined as
, with respect to the minimum risk improved estimator under the ILL is defined as
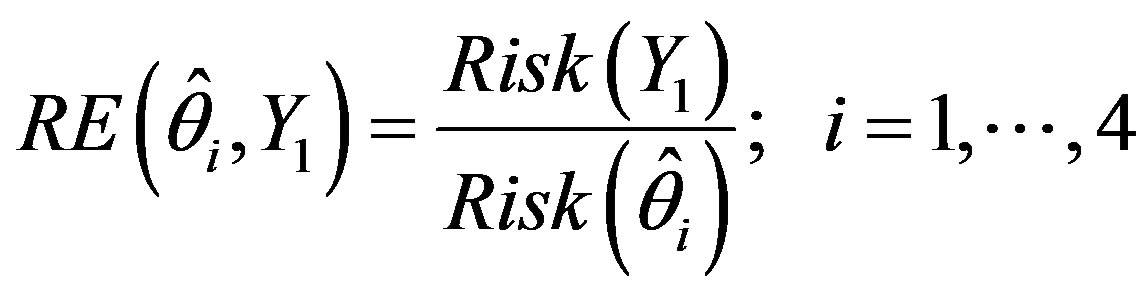
The expression for the relative efficiency ;
;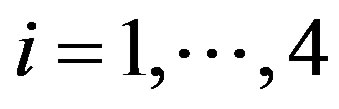 , is the function of
, is the function of 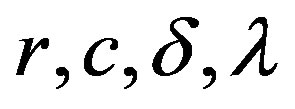 and
and . For the selected values of
. For the selected values of ;
;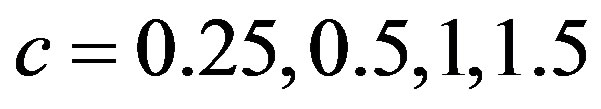 ;
;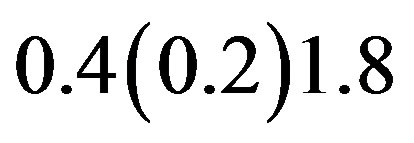
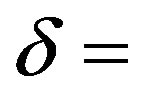 ;
; 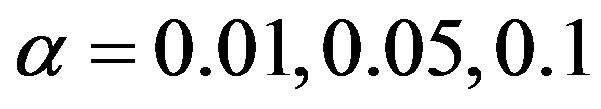 and
and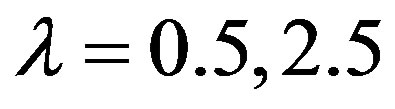 , the relative efficiencies have been calculated and presented in Tables 1-8. Only positive values of
, the relative efficiencies have been calculated and presented in Tables 1-8. Only positive values of  are considered because overestimation in mean life is more serious
are considered because overestimation in mean life is more serious

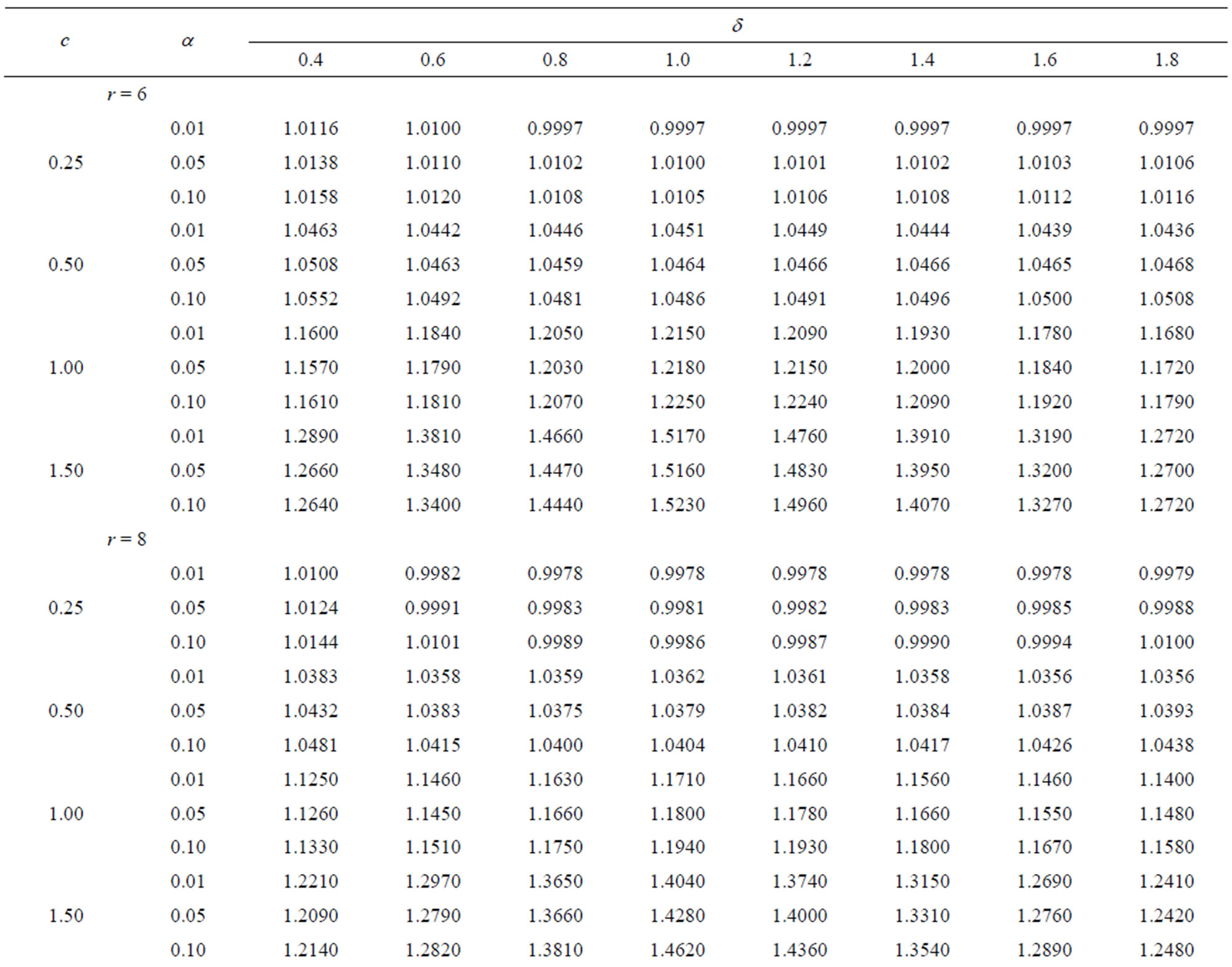
Table 1.  when
when .
.
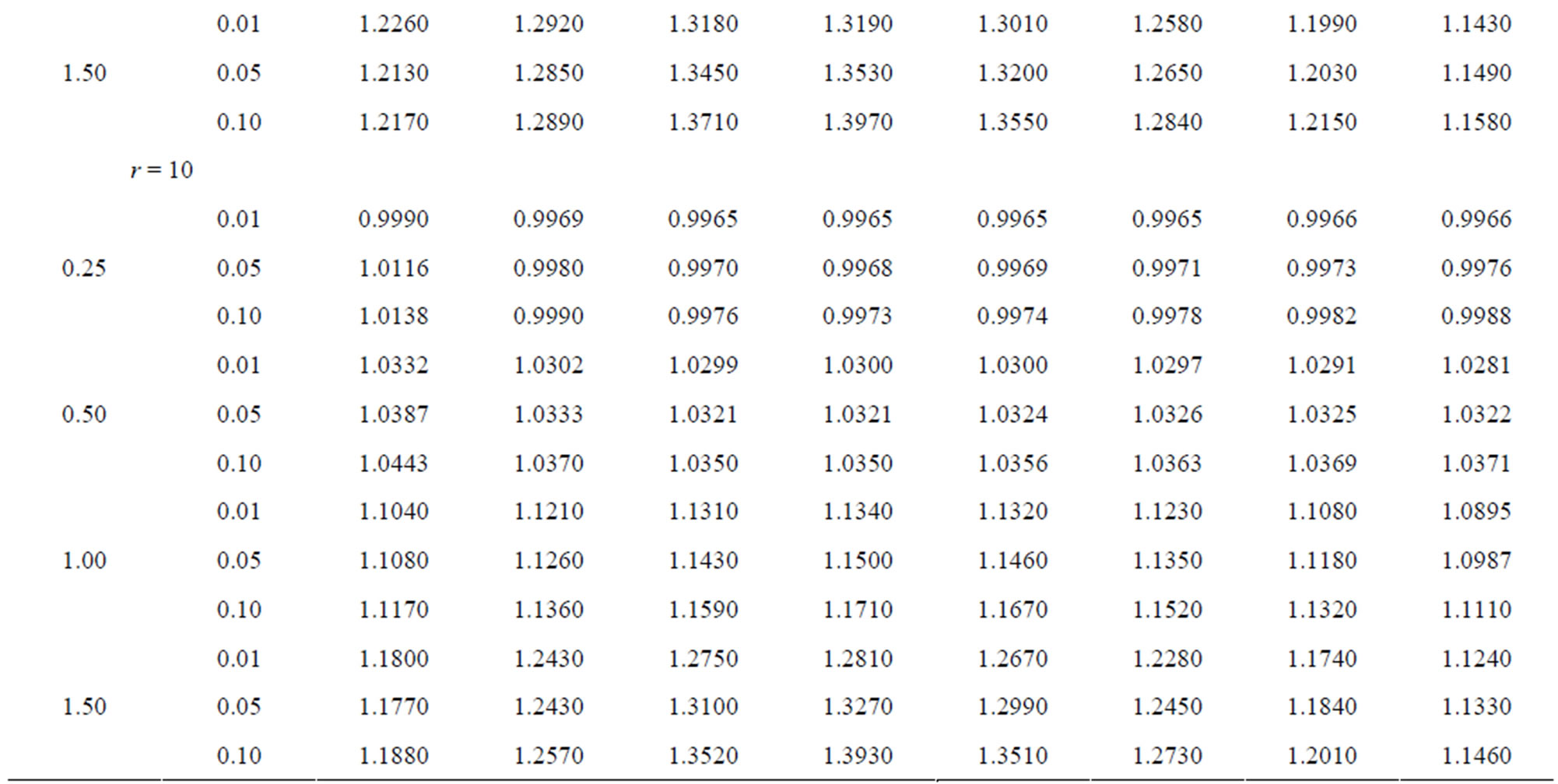
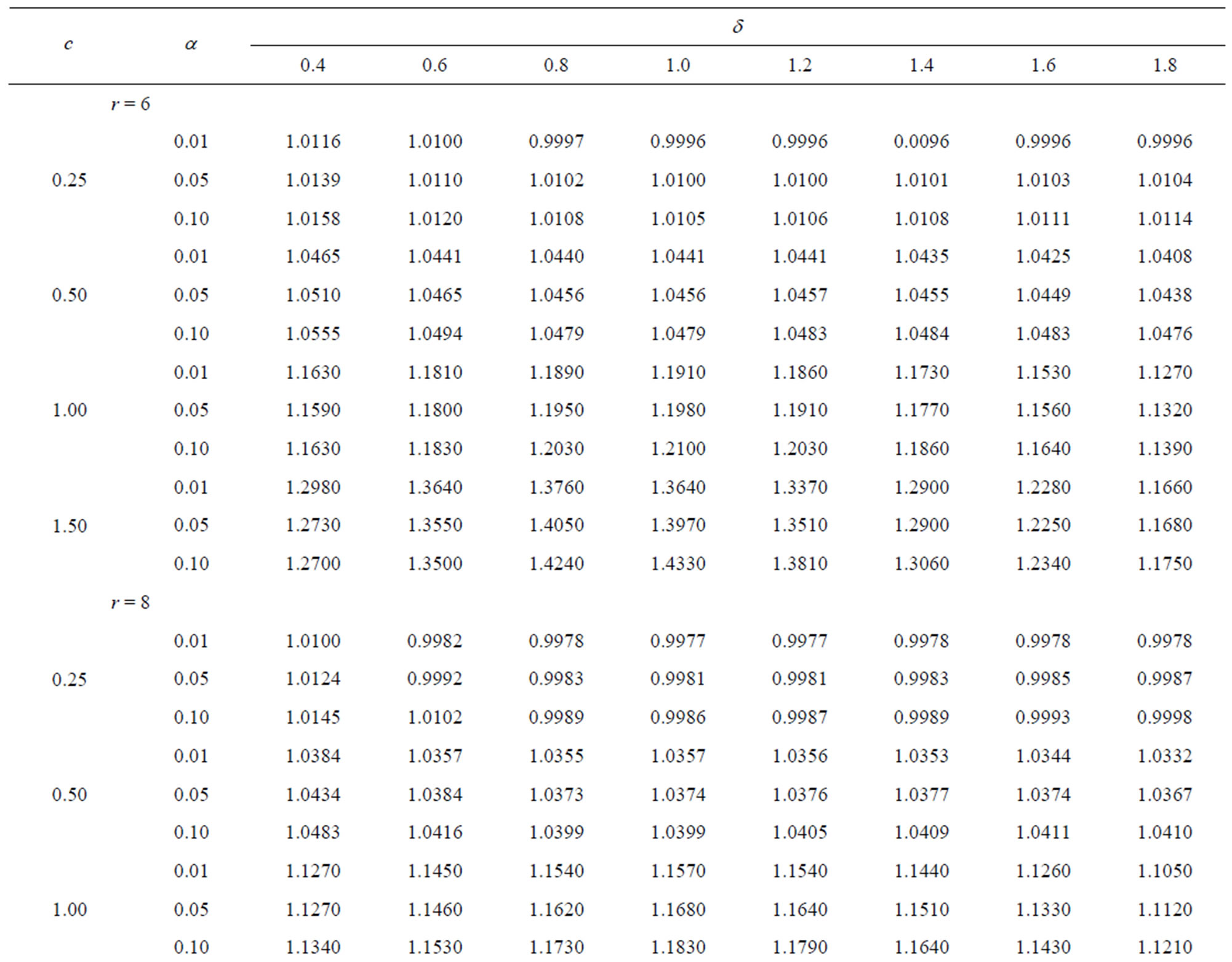
Table 2. 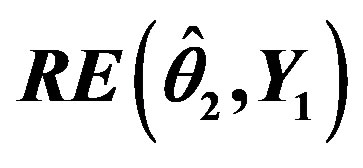 when
when .
.
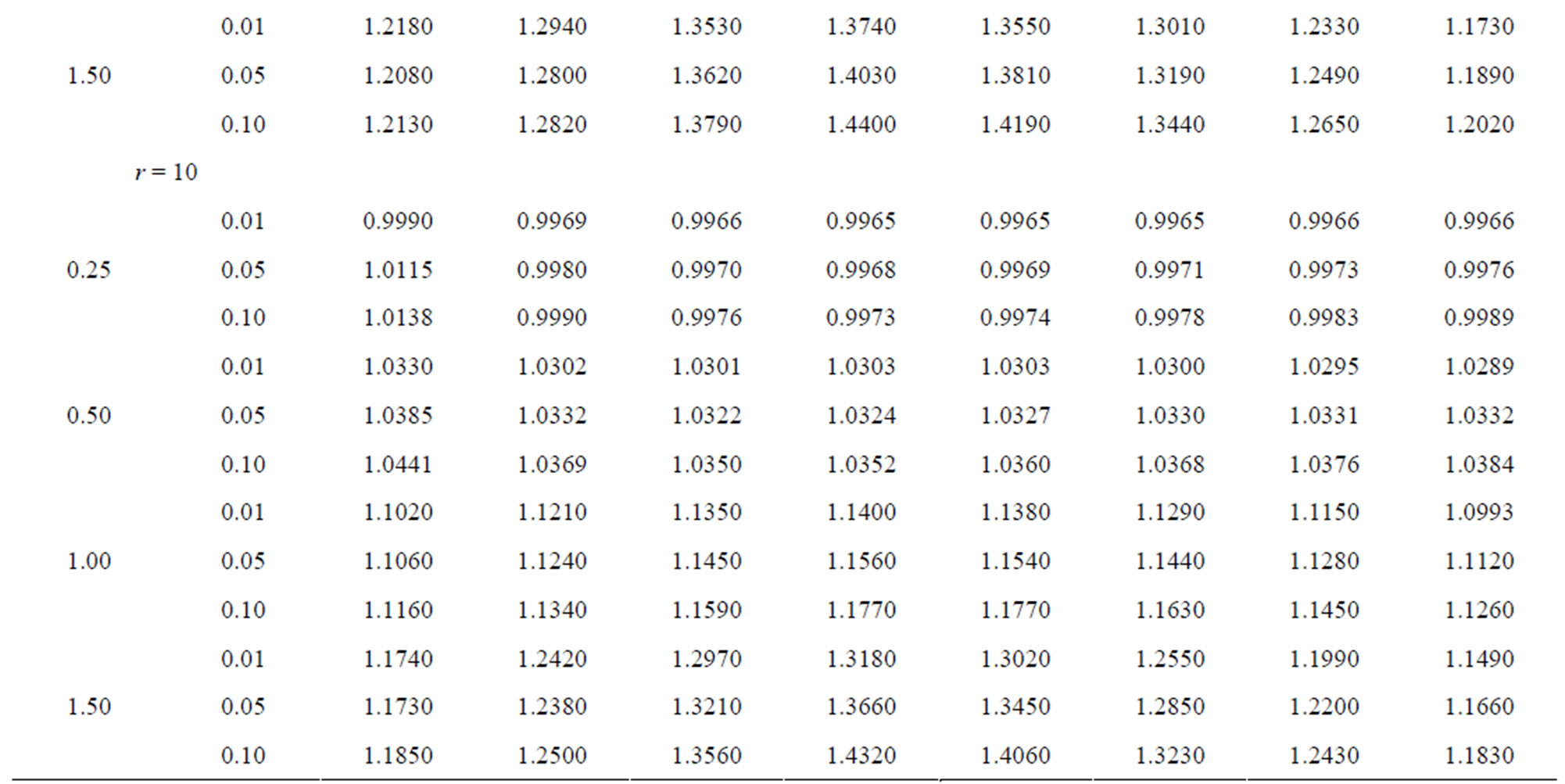

Table 3. 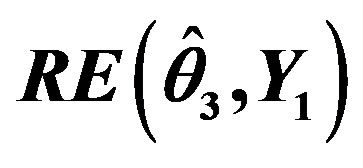 when
when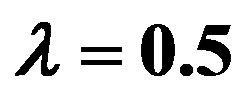 .
.

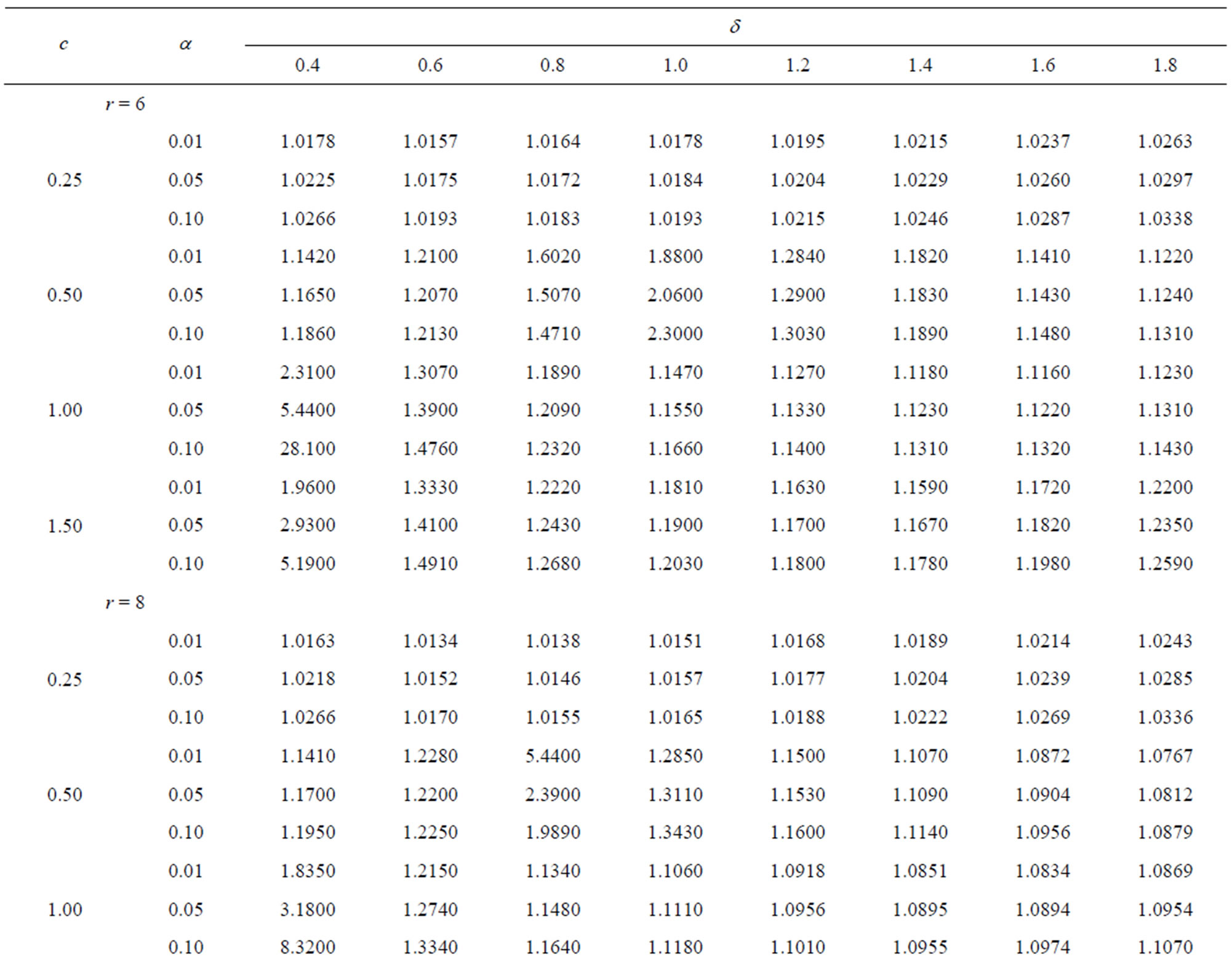
Table 4.  when
when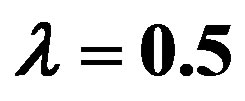 .
.


Table 5. 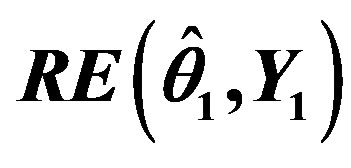 when
when .
.
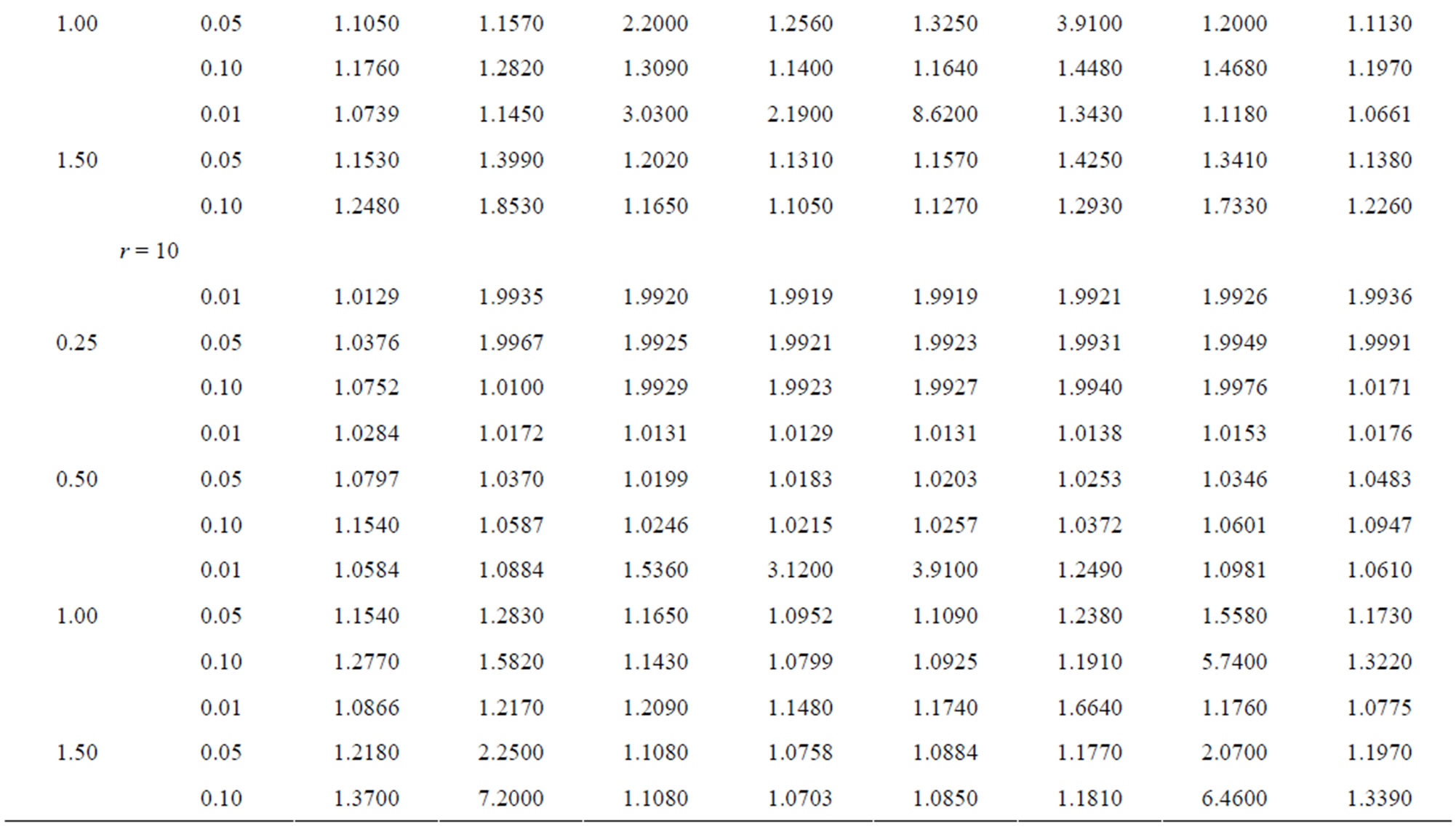

Table 6.  when
when .
.

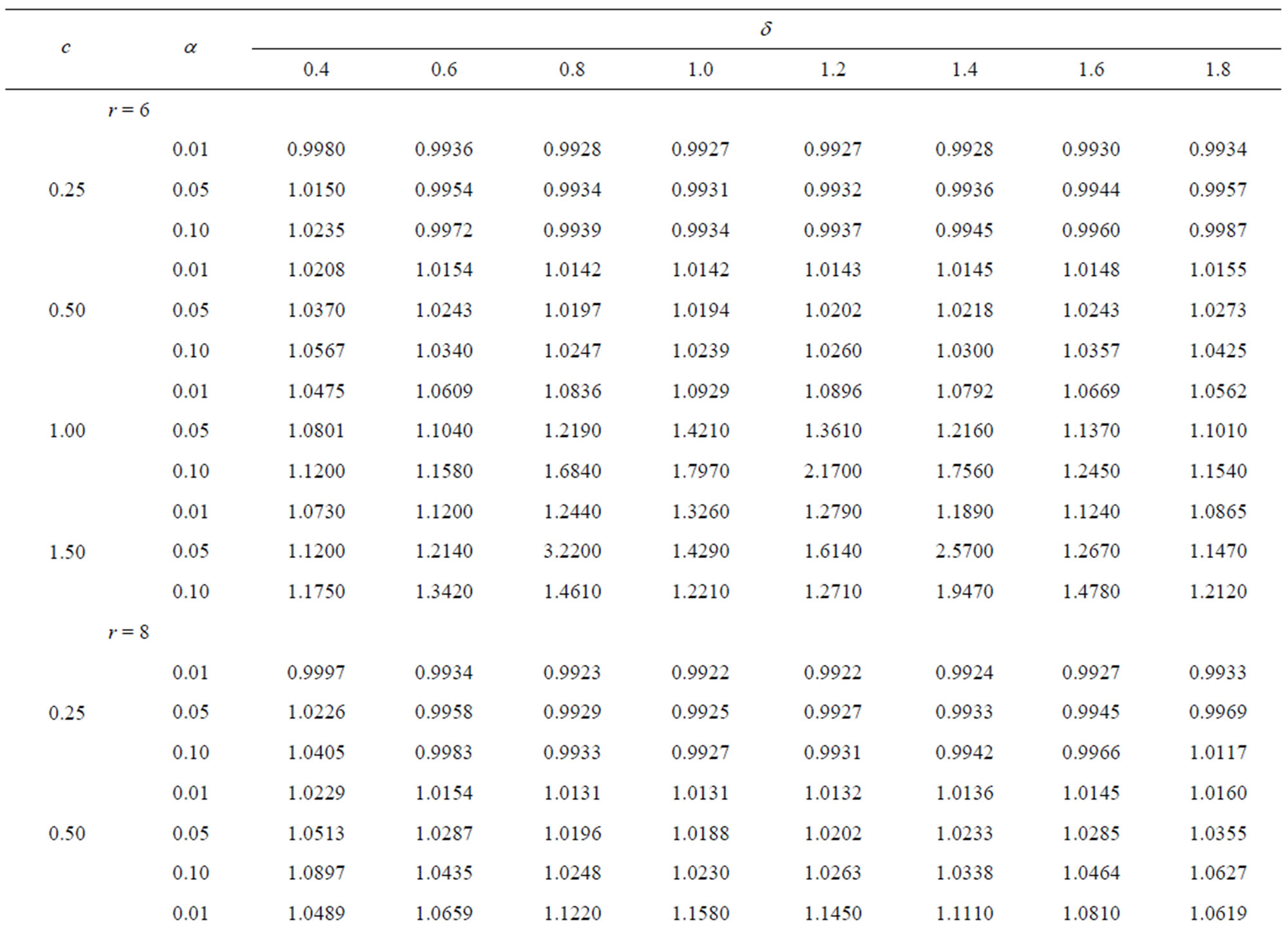
Table 7. 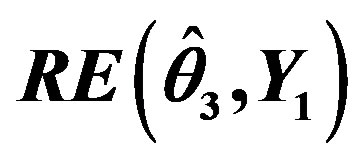 when
when .
.
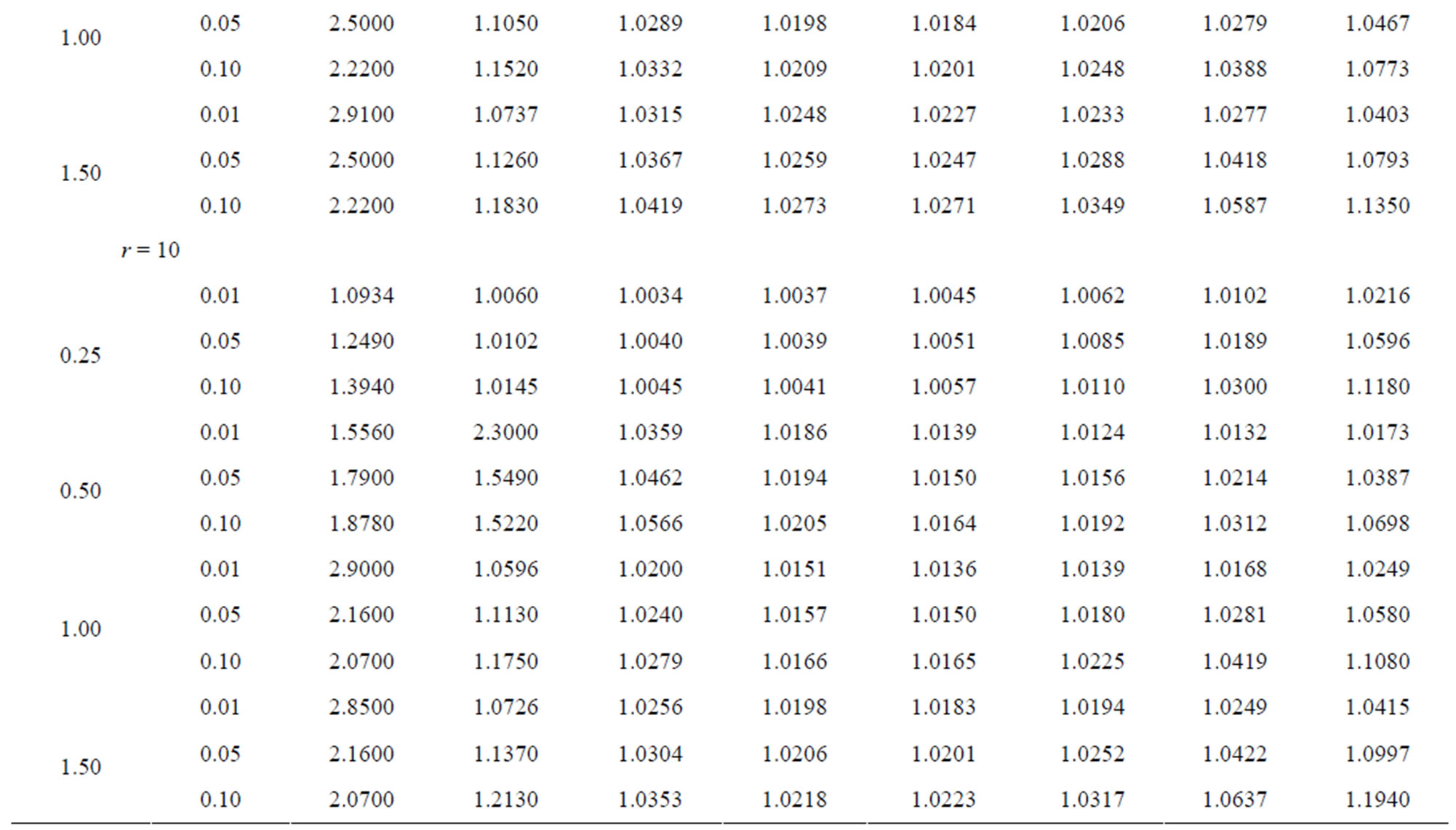

Table 8.  when
when .
.
than the underestimation.
3.1. When 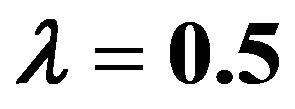
From these tables it is observed that the shrinkage testimators  perform better than the improved estimator
perform better than the improved estimator  for all considered values of
for all considered values of  and α. The testimators
and α. The testimators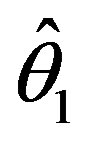 ,
, 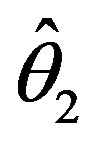 and
and  perform better than
perform better than  when
when . The testimators
. The testimators  attain maximum efficiency at the point δ = 0.4 and others near to the point δ = 1.
attain maximum efficiency at the point δ = 0.4 and others near to the point δ = 1.
For fixed c and level of significance α, as the uncensored sample size r increases, the relative efficiency decreases in all considered values of δ for all the testimators.
For fixed r and α, when c increases the relative efficiency increases in all considered values of δ for all testimators.
It has been seen that as the level of significance α increases the relative efficiency increases in all considered values of δ for all testimators.
3.2. When 
From these tables it is observed that the shrinkage testimators  perform better than the improved estimator
perform better than the improved estimator  for all considered values of
for all considered values of 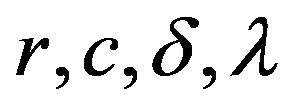 and α. The testimators
and α. The testimators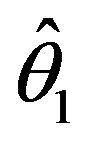 ,
, 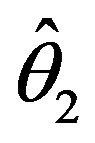 and
and 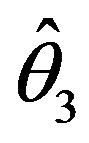 perform better than
perform better than 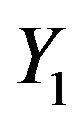 when
when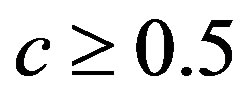 . The testimators
. The testimators 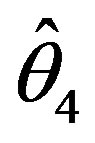 attain maximum efficiency at the point
attain maximum efficiency at the point 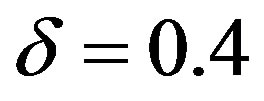 and others near to the point
and others near to the point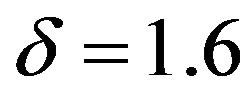 .
.
For fixed  and level of significance α, as the uncensored sample size r increases, the relative efficiency decreases in the region
and level of significance α, as the uncensored sample size r increases, the relative efficiency decreases in the region  for the testimator
for the testimator , and in the region
, and in the region 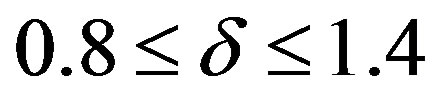 for the testimators
for the testimators 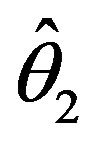 and
and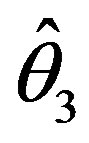 , and also for testimator
, and also for testimator  it decreases for all considered values of δ.
it decreases for all considered values of δ.
For fixed r and α, when c increases the relative efficiency increases in all considered values of δ for all testimators.
It has been seen that as the level of significance α increases the relative efficiency increases in  and also in
and also in 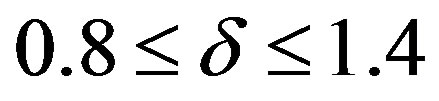 when
when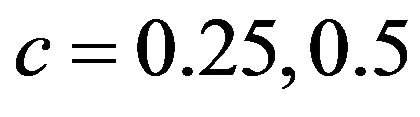 , and decreases for
, and decreases for  when
when  and
and 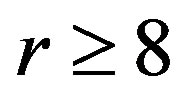 for testimators
for testimators ,
,  and
and , and for testimator
, and for testimator 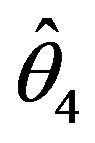 it increases for all considered values of δ.
it increases for all considered values of δ.
4. Recommendations
In this study, some shrinkage testimators ( ,
, 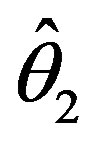 ,
, 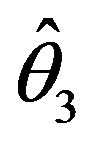 and
and ) for the scale parameter of a gamma distribution, when type-II censored data are available, suggested that under the ILL loss function assuming the shape parameter was to be known. The comparisons of the proposed testimators made with improved estimator
) for the scale parameter of a gamma distribution, when type-II censored data are available, suggested that under the ILL loss function assuming the shape parameter was to be known. The comparisons of the proposed testimators made with improved estimator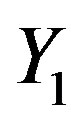 . The recommendations have been presented, based on the relative efficiency for all the shrinkage testimator. From the previous observations, the shrinkage testimators
. The recommendations have been presented, based on the relative efficiency for all the shrinkage testimator. From the previous observations, the shrinkage testimators 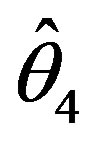 perform better than the improved estimator
perform better than the improved estimator  for all considered values of
for all considered values of  and α, and the testimators
and α, and the testimators ,
, 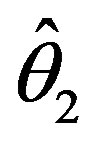 and
and  perform better than
perform better than  when
when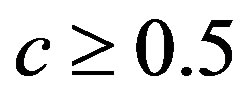 . Since the shrinkage testimators
. Since the shrinkage testimators 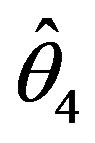 always perform better than other shrinkage testimators if the gain in efficiency does not matter, therefore we strongly suggest using the shrinkage testimators
always perform better than other shrinkage testimators if the gain in efficiency does not matter, therefore we strongly suggest using the shrinkage testimators  for the scale parameter of a gamma distribution, when Type-II censored data are available, suggested under the ILL loss function.
for the scale parameter of a gamma distribution, when Type-II censored data are available, suggested under the ILL loss function.
5. Acknowledgements
The authors would like to thank the referee and the editor for a careful reading of the paper and for valuable comments which improved the presentation of the paper. The second author gratefully appreciates his wife, Dr. Saemeh Dehghan, who kindly helps the researcher in the study.
REFERENCES
- A. Parsian and S. N. U. A. Kirmani, “Estimation under LINEX loss function,” In: A. Ulla, Ed., Handbook of Applied Econometrics and Statistical Inference, 165 Dekker, New York, 2002, pp. 53-76.
- H. Pazira and A. Shadrokh, “Comparison of LINEX and Precautionary Bayes Estimators on the Gamma Distribution Using Censored Data,” Journal of Statistics and Management Systems, Vol. 14, No. 3, 2011, pp. 617-638. doi:10.1080/09720510.2011.10701575
- T. S. Ferguson, “Mathematical Statistics: A Decision Theoretic Approach,” Academic Press, New York, 1967.
- A. Zellner and M.S. Geisel, “Sensitivity of Control to Uncertainty and Form of the Criterion Function,” In the future of statistics, Ed Donald G. Watts, Academic Press, New York, 1968, pp. 269-289.
- J. Aitchison and I. R. Dunsmore, “Statistical Prediction Analysis,” Cambridge University Press, Cambridge, 1975. doi:10.1017/CBO9780511569647
- H. R. Varian, “A Bayesian Approach to Real Estate Assessment,” In: L. J. Savage, S. E. Feinberg and A. Zellner, Eds., Studies in Bayesian Econometrics and Statistics: In Honor of L. J. Savage, North-Holland Pub. Co., Amsterdam, 1975, pp. 195-208.
- J. O. Berger, “Statistical Decision Theory-Foundation Concepts and Methods,” Springer-Verlag, New York, 1980. doi:10.1007/978-1-4757-1727-3
- A. P. Basu and N. Ebrahimi, “Bayesian Approach to Life Testing and Reliability Estimation Using Asymmetric Loss Function,” Journal of Statistical Planning and Inferences, Vol. 29, No. 1-2, 1991, pp. 21-31. doi:10.1016/0378-3758(92)90118-C
- B. N. Pandey, “Testimator of the Scale Parameter of the Exponential Distribution Using LINEX Loss Function,” Communication in Statistics-Theory and Methods, Vol. 26, No. 6, 1997, pp. 2191-2202. doi:10.1016/0026-2714(88)90294-6
- A. A. Soliman, “Comparison of Linex and QuadraticBayes Estimators Foe the Rayleigh Distribution,” Communication in Statistics-Theory and Methods, Vol. 29, No. 1, 2000, pp. 95-107. doi:10.1080/03610920008832471
- G. Prakash and D. C. Singh, “Shrinkage Estimation in Exponential Type-II Censored Data under LINEX Loss,” Journal of the Korean Statistical Society, Vol. 37, No. 1, 2008, pp. 53-61. doi:10.1016/j.jkss.2007.07.002
- A. Parsian and N. S. Farsipour, “Estimation of the Mean of the Selected Population under Asymmetric Loss Function,” Metrika, Vol. 50, No. 2, 1999, pp. 89-107.
- U. Singh, P. K. Gupta and S. K. Upadhyay, “Estimation of Exponentiated Weibull Shape Parameters under LINEX Loss Function,” Communication in Statistics-Simulation, Vol. 31, No. 4, 2002, pp. 523-537. doi:10.1081/SAC-120004310
- N. Misra and E. V. D. Meulen, “On Estimating the Mean of the Selected Normal Population under the LINEX Loss Function,” Metrika, Vol. 26, No. 9, 2003, pp. 173-184. doi:10.1080/03610929708832041
- J. Ahmadi, M. Doostparast and A. Parsian, “Estimation and Prediction in a Two-Parameter Exponential Distribution Based on K-Record Values under LINEX Loss Function,” Communications in Statistics-Theory and Methods, Vol. 34, No. 4, 2005, pp. 795-805. doi:10.1081/STA-200054393
- Y. Xiao, Y. Takada and N. Shi, “Minimax Confidence Bound of the Normal Mean under an Asymmetric Loss Function,” Annals of Statistical Mathematics, Vol. 57, No. 1, 2005, pp. 167-182. doi:10.1007/BF02506886
- D. C. Singh, G. Prakash and P. Singh, “Shrinkage Testimator for the Shape Parameter of Pareto Distribution Using LINEX Loss Function,” Communication in Statistics-Theory and Methods, Vol. 36, No. 4, 2007, pp. 741- 753. doi:10.1080/03610920601033694
- A. K. Rao and R. S. Srivastava, “Bayesian Estimation of the Scale Parameter of Gamma Distribution under Linex Loss Function with Censoring,” In: B. N. Pandey, Ed., Statistical Techniques in Life-Testing, Reliability, Sampling Theory and Quality Control, Narosa Pub House, Daryaganj, 2002, pp. 287-295.
- J. R. Thompson, “Some Shrunken Techniques for Estimateing the Mean,” Journal of the American Statistical Association, Vol. 63, No. 321, 1968, pp. 113-122. doi:10.2307/2283832
- V. B. Waikar, F. J. Schuurmann and T. E. Raghunathan, “On a Two Stage Shrunken Testimator of the Mean of a Normal Distribution,” Communications in Statistics-Theory and Methods, Vol. 13, No. 15, 1984, pp. 1901-1913. doi:10.1080/03610928408828802
- S. R. Adke, V. B. Waikar and F. J. Schuurmann, “A Two Stage Shrinkage Testimator for the Mean of an Exponential Distribution,” Communication in Statistics-Theory and Methods, Vol. 16, No. 6, 1987, pp. 1821-1834. doi:10.1080/03610928708829474
- B. N., Pandey, H. J. Malik and R. Srivastava, “Shrinkage Testimator for the Variance of a Normal Distribution at Single and Double Stages,” Microelectron Reliability, Vol. 28, No. 6, 1988, pp. 929-944. doi:10.1016/0026-2714(88)90294-6

