Open Journal of Statistics
Vol.2 No.5(2012), Article ID:25544,7 pages DOI:10.4236/ojs.2012.25062
Complete Convergence and Weak Law of Large Numbers for 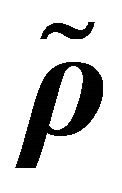 -Mixing Sequences of Random Variables
-Mixing Sequences of Random Variables
1College of Science, Guilin University of Technology, Guilin, China
2Guangxi Key Laboratory of Spatial Information and Geomatics, Guilin, China
Email: wqy666@glut.edu.cn
Received September 5, 2012; revised October 7, 2012; accepted October 20, 2012
Keywords: 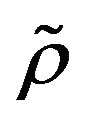 -Mixing Sequence of Random Variables; Complete Convergence; Weak Law of Large Number
-Mixing Sequence of Random Variables; Complete Convergence; Weak Law of Large Number
ABSTRACT
In this paper, the complete convergence and weak law of large numbers are established for 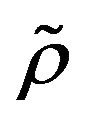 -mixing sequences of random variables. Our results extend and improve the Baum and Katz complete convergence theorem and the classical weak law of large numbers, etc. from independent sequences of random variables to
-mixing sequences of random variables. Our results extend and improve the Baum and Katz complete convergence theorem and the classical weak law of large numbers, etc. from independent sequences of random variables to 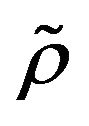 -mixing sequences of random variables without necessarily adding any extra conditions.
-mixing sequences of random variables without necessarily adding any extra conditions.
1. Introduction
Let  be a probability space. The random variables we deal with are all defined on
be a probability space. The random variables we deal with are all defined on . Let
. Let 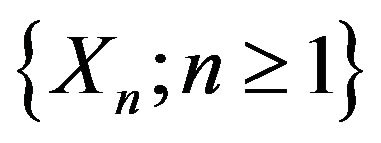 be a sequence of random variables. For each nonempty set
be a sequence of random variables. For each nonempty set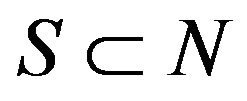 , write
, write . Given
. Given ![]() -algebras
-algebras 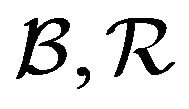 in
in , let
, let
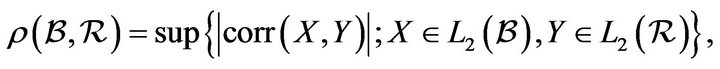
where . Define the
. Define the  -mixing coefficients by
-mixing coefficients by
 (1.1)
(1.1)
where (for a given positive integer![]() ) this sup is taken over all pairs of nonempty finite subsets
) this sup is taken over all pairs of nonempty finite subsets  such that dist
such that dist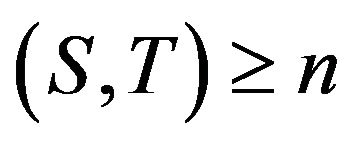 .
.
Obviously 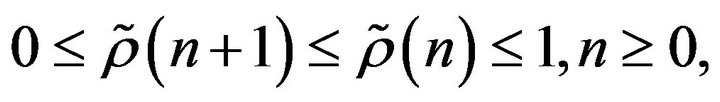 and
and 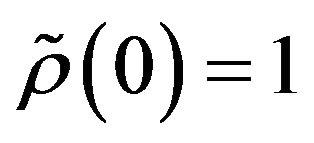 except in the trivial case where all of the random variables
except in the trivial case where all of the random variables 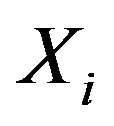 are degenerate.
are degenerate.
Definition 1.1. A sequence of random variables  is said to be a
is said to be a  -mixing sequence of random variables if there exists
-mixing sequence of random variables if there exists 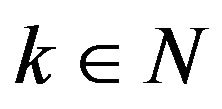 such that
such that .
.
Without loss of generality we may assume that 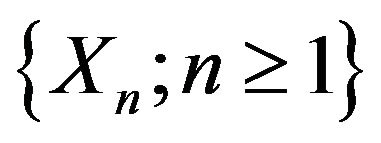 is such that
is such that 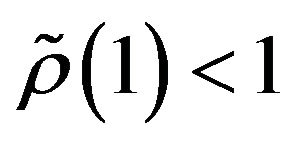 (see [1]). Here we give two examples of the practical application of
(see [1]). Here we give two examples of the practical application of 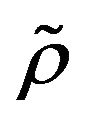 - mixing.
- mixing.
Example 1.1. According to the proof of Theorem 2 in [2] and Remark 3 in [1], if 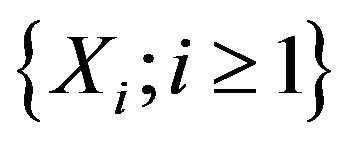 is a strictly stationary Gaussian sequence which has a bounded positive spectral density
is a strictly stationary Gaussian sequence which has a bounded positive spectral density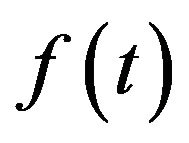 , then the sequence
, then the sequence
 has the property that
has the property that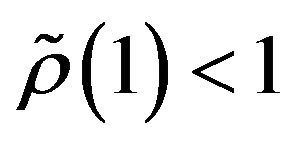 . Therefore, instantaneous functions
. Therefore, instantaneous functions 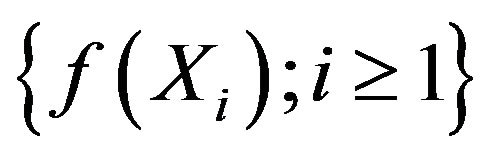 of such a sequence provides a class of examples for
of such a sequence provides a class of examples for 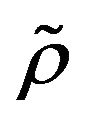 -mixing sequences.
-mixing sequences.
Example 1.2. If 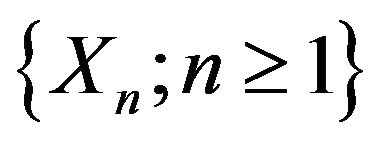 has a bounded positive spectral density
has a bounded positive spectral density , i.e.,
, i.e., 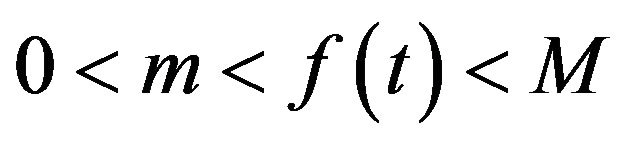 for every t, then
for every t, then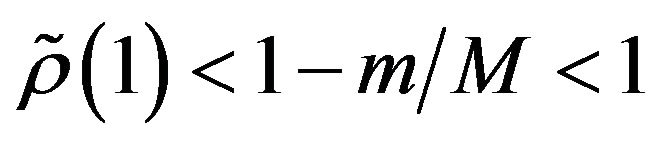 . Thus,
. Thus, 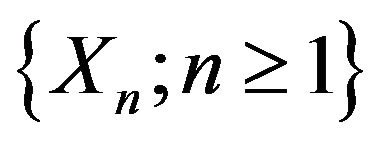 is a
is a 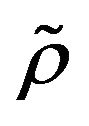 -mixing sequence.
-mixing sequence.
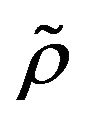 -mixing is similar to
-mixing is similar to  -mixing, but both are quite different.
-mixing, but both are quite different. 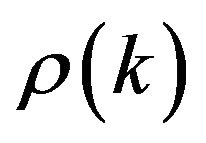 is defined by (1.1) with index sets restricted to subsets S of
is defined by (1.1) with index sets restricted to subsets S of  and subsets
and subsets ![]() of
of . On the other hand,
. On the other hand,  -mixing sequence assume condition
-mixing sequence assume condition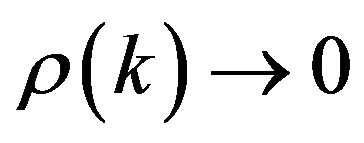 ,but
,but  -mixing sequence assume condition that there exists
-mixing sequence assume condition that there exists 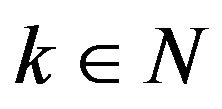 such that
such that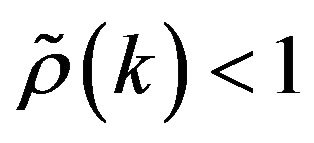 , from this point of view,
, from this point of view, 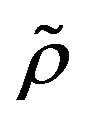 -mixing is weaker than
-mixing is weaker than  -mixing.
-mixing.
A number of writers have studied 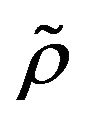 -mixing sequences of random variables and a series of useful results have been established. We refer to [2] for the central limit theorem [1,3], for moment inequalities and the strong law of large numbers [4-9], for almost sure convergence, and [10] for maximal inequalities and the invariance principle. When these are compared with the corresponding results for sequences of independent random variables, there still remains much to be desired.
-mixing sequences of random variables and a series of useful results have been established. We refer to [2] for the central limit theorem [1,3], for moment inequalities and the strong law of large numbers [4-9], for almost sure convergence, and [10] for maximal inequalities and the invariance principle. When these are compared with the corresponding results for sequences of independent random variables, there still remains much to be desired.
The main purpose of this paper is to study the complete convergence and weak law of large numbers of partial sums of 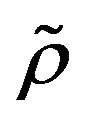 -mixing sequences of random variables and try to obtain some new results. We establish the complete convergence theorems and the weak law of large numbers. Our results in this paper extend and improve the corresponding results of Feller [11] and Baum and Katz [12].
-mixing sequences of random variables and try to obtain some new results. We establish the complete convergence theorems and the weak law of large numbers. Our results in this paper extend and improve the corresponding results of Feller [11] and Baum and Katz [12].
Lemma 1.1. ([10], Theorem 2.1) Suppose K is a positive integer, 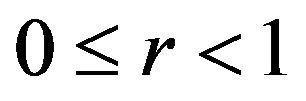 , and
, and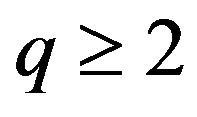 . Then there exists a positive constant
. Then there exists a positive constant  such that the following statement holds:
such that the following statement holds:
If  is a sequence of random variables such that
is a sequence of random variables such that 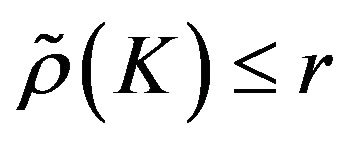 and
and 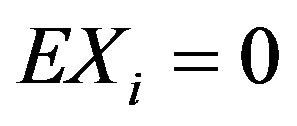 and
and 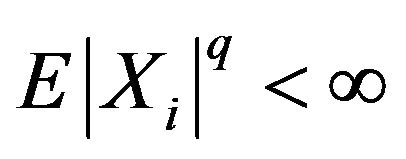 for all
for all![]() , then for every
, then for every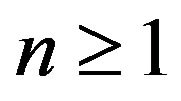 ,
,

where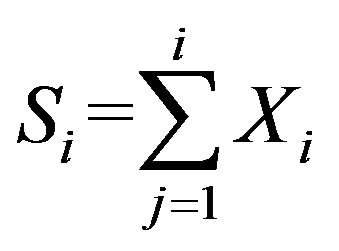 .
.
Lemma 1.2. Let  be a
be a 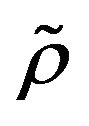 -mixing sequence of random variables. Then for any
-mixing sequence of random variables. Then for any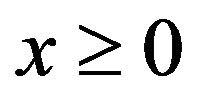 , there exists a positive constant c such that for all
, there exists a positive constant c such that for all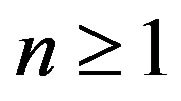 ,
,

Proof. Let 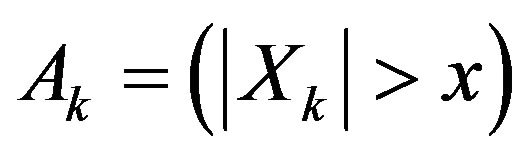 and
and
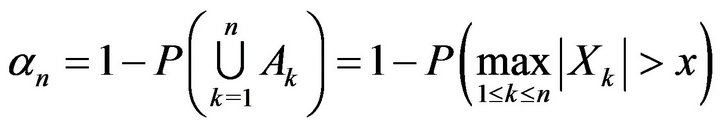 . Without loss of generality, assume that
. Without loss of generality, assume that . By the Cauchy-Schwarz inequality and Lemma 1.2,
. By the Cauchy-Schwarz inequality and Lemma 1.2,

Thus
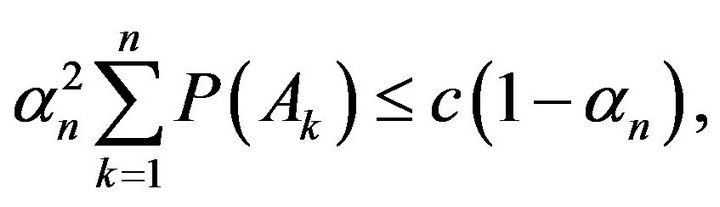
i.e.,
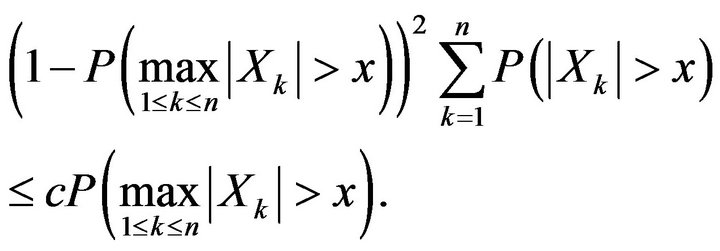
2. Complete Convergence
In the following, let 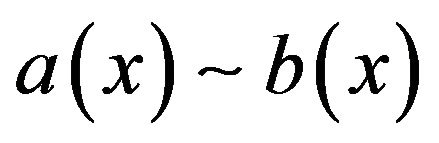 denote
denote
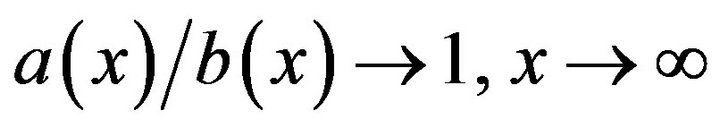 , and
, and 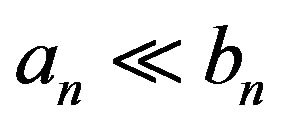
 denote that there exists a constant
denote that there exists a constant  such that
such that 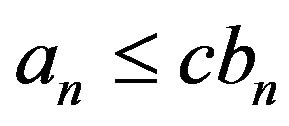
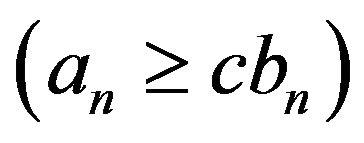 for sufficiently large n, logx mean
for sufficiently large n, logx mean
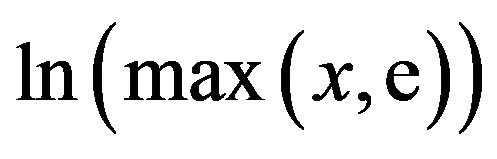 , and
, and .
.
Definition 2.1. A measurable function  is said to be a slowly varying function at
is said to be a slowly varying function at  if for any
if for any
 ,
, .
.
Lemma 2.1 ([13], Lemma 1). Let 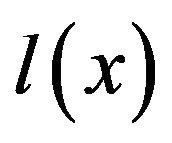 be a slowly varying function at
be a slowly varying function at . Then i)
. Then i) .
.
ii) 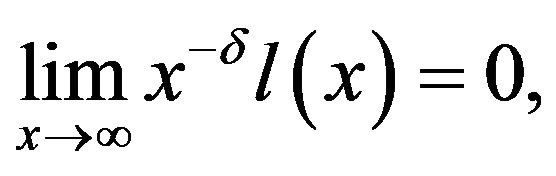
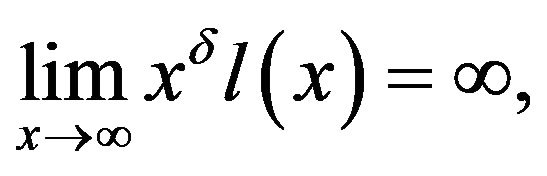 for any
for any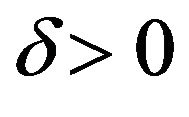 .
.
iii) For any 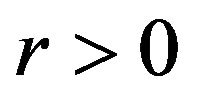 and
and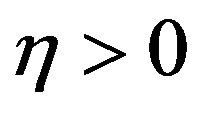 , there exist positive constants
, there exist positive constants ![]() and
and 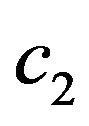 (depending only on
(depending only on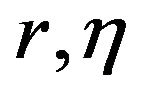 , and the function
, and the function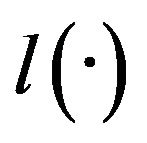 ) such that for any positive number k,
) such that for any positive number k,

iv) For any 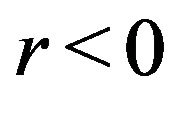 and
and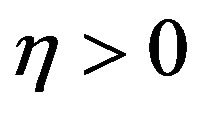 , there exist positive constants
, there exist positive constants 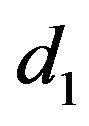 and
and 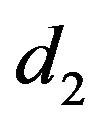 (depending only on
(depending only on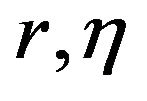 , and the function
, and the function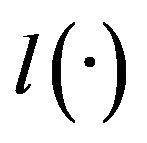 ) such that for any positive number k,
) such that for any positive number k,
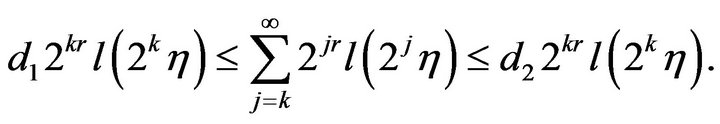
Theorem 2.1. Let 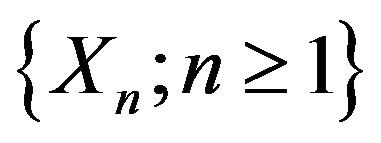 be a
be a 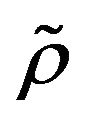 -mixing sequence of identically distributed random variables. Suppose that
-mixing sequence of identically distributed random variables. Suppose that  is a slowly varying function at
is a slowly varying function at , and also assume that for each
, and also assume that for each , the function
, the function 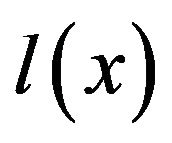 is bounded on the interval
is bounded on the interval . Suppose
. Suppose  and
and ; and if
; and if 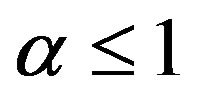 then suppose also that
then suppose also that . Then
. Then
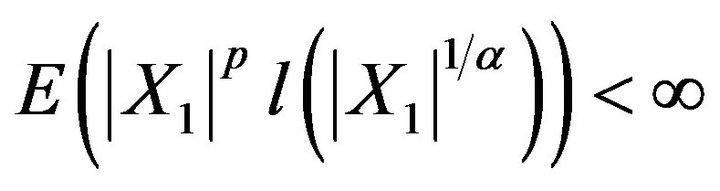 (2.1)
(2.1)
and
 (2.2)
(2.2)
are equivalent.
For 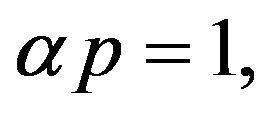 we also have the following theorem under adding the condition that
we also have the following theorem under adding the condition that  is a monotone nondecreasing function.
is a monotone nondecreasing function.
Theorem 2.2. Let 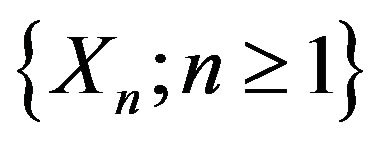 be a
be a  -mixing sequence of identically distributed random variables. Let
-mixing sequence of identically distributed random variables. Let 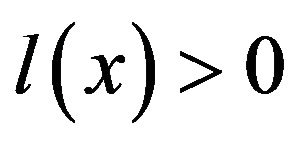 is a slowly varying function at
is a slowly varying function at  and monotone non-decreasing function. Suppose
and monotone non-decreasing function. Suppose ; and if
; and if 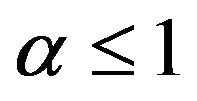 then suppose also that
then suppose also that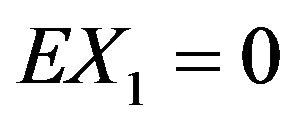 . Then
. Then
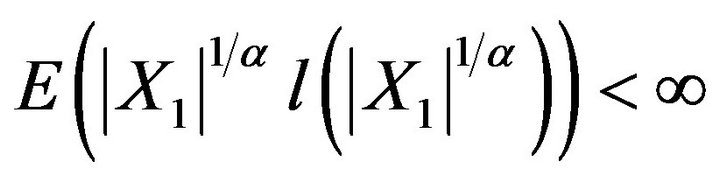 (2.3)
(2.3)
and
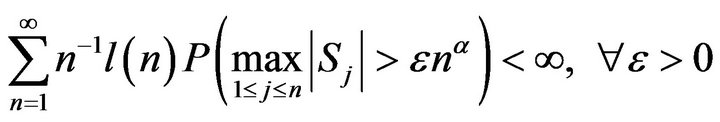 (2.4)
(2.4)
are equivalent.
Taking 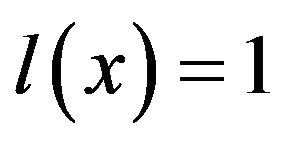 and
and 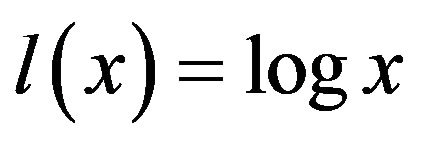 respectively in Theorems 2.1 and 2.2 we can immediately obtain the following corollaries.
respectively in Theorems 2.1 and 2.2 we can immediately obtain the following corollaries.
Corollary 2.1. Let 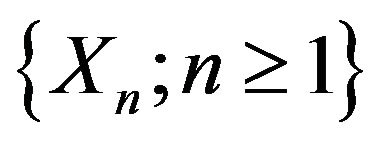 be a
be a 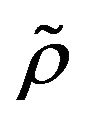 -mixing sequence of identically distributed random variables. Suppose
-mixing sequence of identically distributed random variables. Suppose 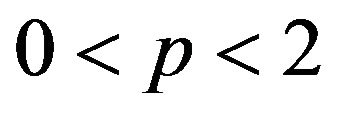 and
and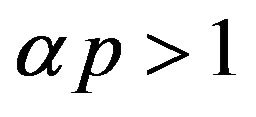 ; and if
; and if 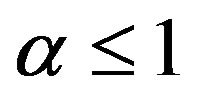 then suppose also that
then suppose also that . Then
. Then
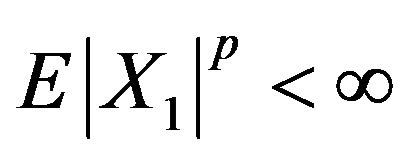
and
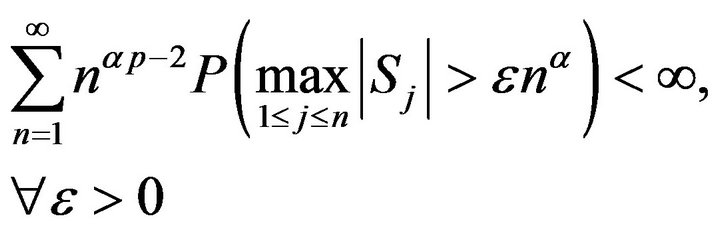
are equivalent.
Corollary 2.2. Let 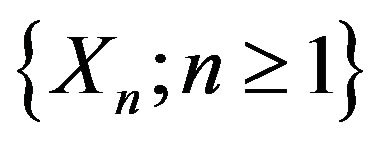 be a
be a  -mixing sequence of identically distributed random variables. Suppose
-mixing sequence of identically distributed random variables. Suppose 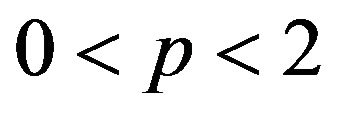 and
and ; and if
; and if 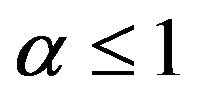 then suppose also that
then suppose also that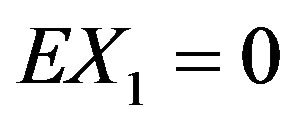 . Then
. Then
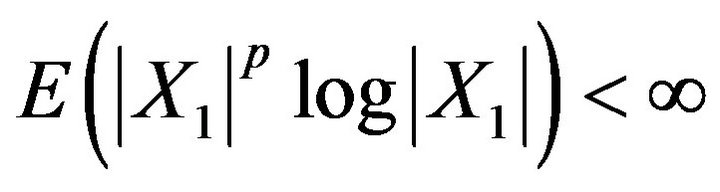
and
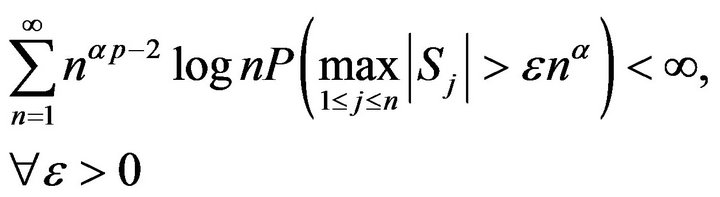
are equivalent.
Remark 2.1. When 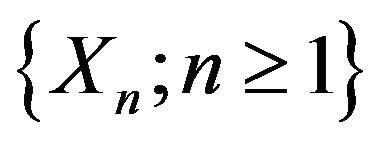 i.i.d., Corollary 2.5 becomes the Baum and Katz [12] complete convergence theorem. So Theorems 2.1 and 2.2 extend and improve the Baum and Katz complete convergence theorem from the i.i.d. case to
i.i.d., Corollary 2.5 becomes the Baum and Katz [12] complete convergence theorem. So Theorems 2.1 and 2.2 extend and improve the Baum and Katz complete convergence theorem from the i.i.d. case to  -mixing sequences.
-mixing sequences.
Remark 2.2. Letting  take various forms in Theorems 2.1 and 2.2, we can get a variety of pairs of equivalent statements, one involving a moment condition and the other involving a complete convergence condition.
take various forms in Theorems 2.1 and 2.2, we can get a variety of pairs of equivalent statements, one involving a moment condition and the other involving a complete convergence condition.
Proof of Theorem 2.1. . Let
. Let
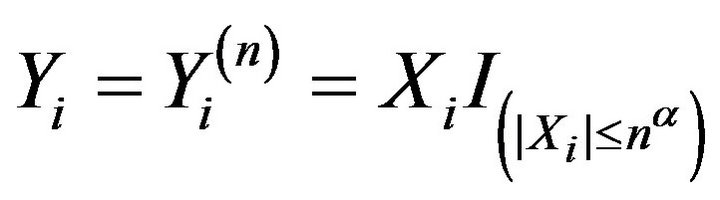 ,
,
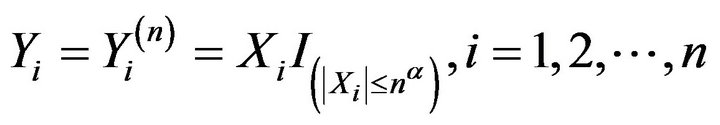 . Firstly, we prove that
. Firstly, we prove that
 (2.5)
(2.5)
By Lemma 2.1 and (2.1), it is easy to show that
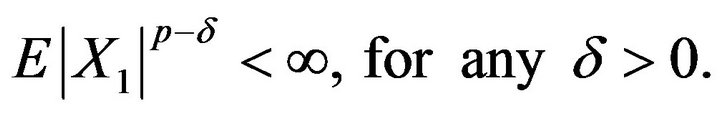 (2.6)
(2.6)
i) For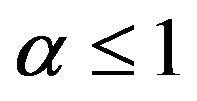 , we have
, we have , and
, and .
.
Let  in (2.6), by
in (2.6), by
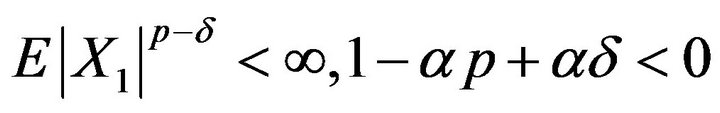 ,
,
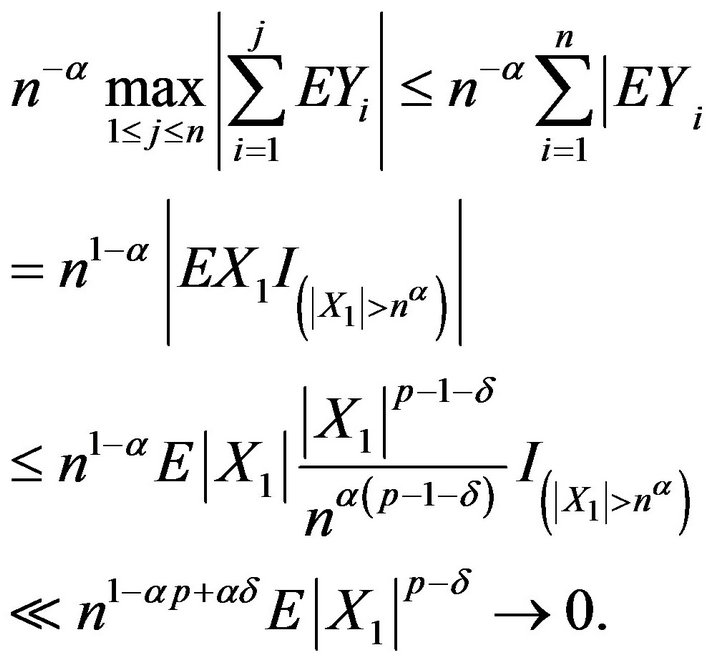
ii) For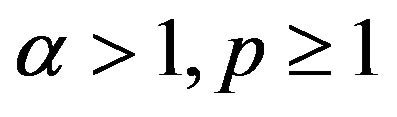 , let
, let 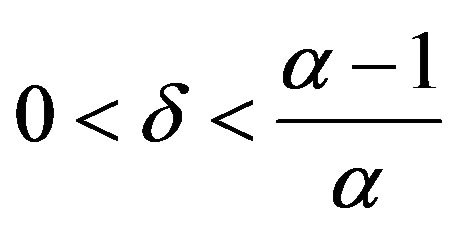 in (2.6), then
in (2.6), then
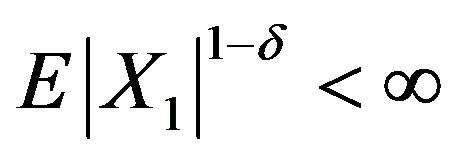 and
and . Hence
. Hence
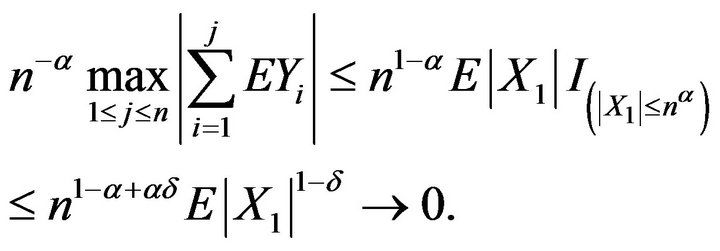
iii) For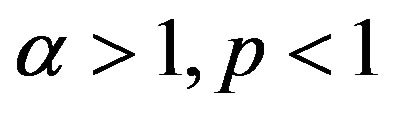 ,
,
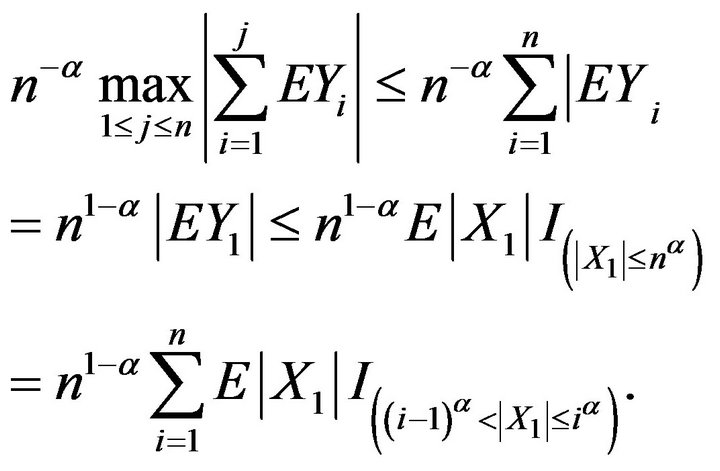
Noting , let
, let  in (2.6). By
in (2.6). By
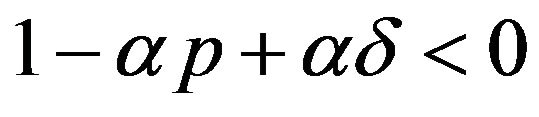 and
and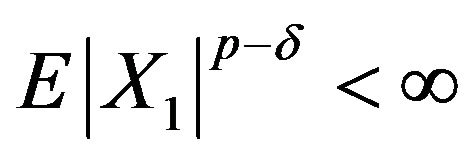 , we get
, we get
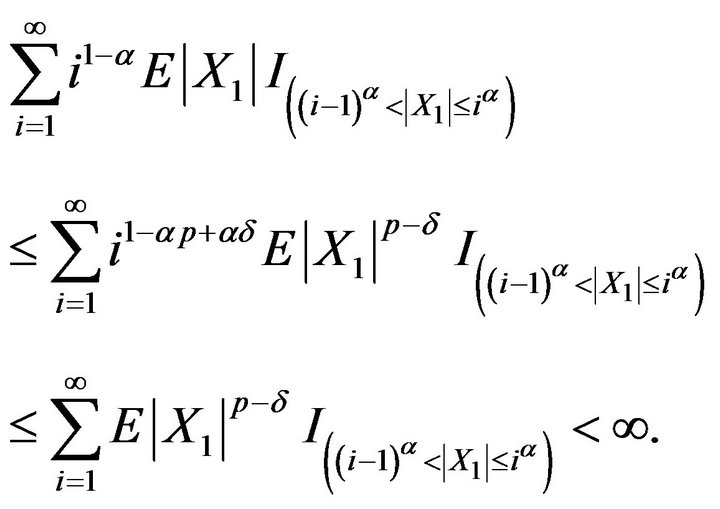
By 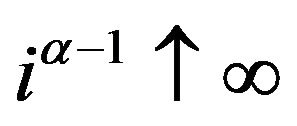 and the Kronecker lemma,
and the Kronecker lemma,
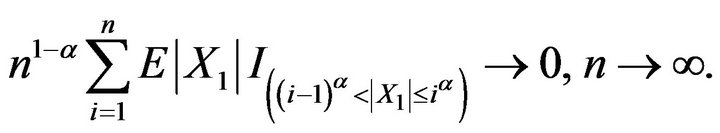
Hence (2.5) holds. So to prove (2.2) it suffices to prove that
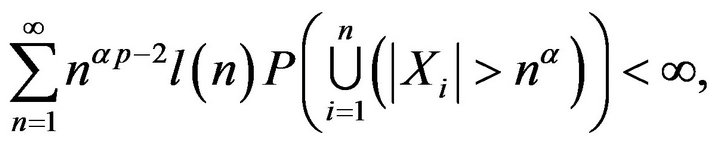 (2.7)
(2.7)
and ,
,
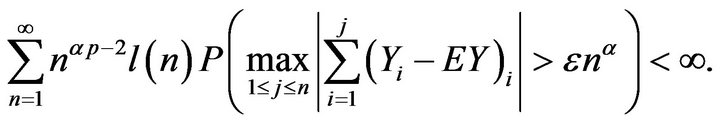 (2.8)
(2.8)
By Lemmas 2.1 (i), (iii), (2.1), and for each , the function
, the function 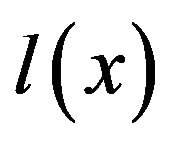 is bounded on the interval
is bounded on the interval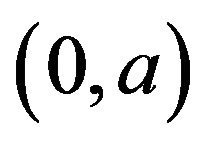 ,
,
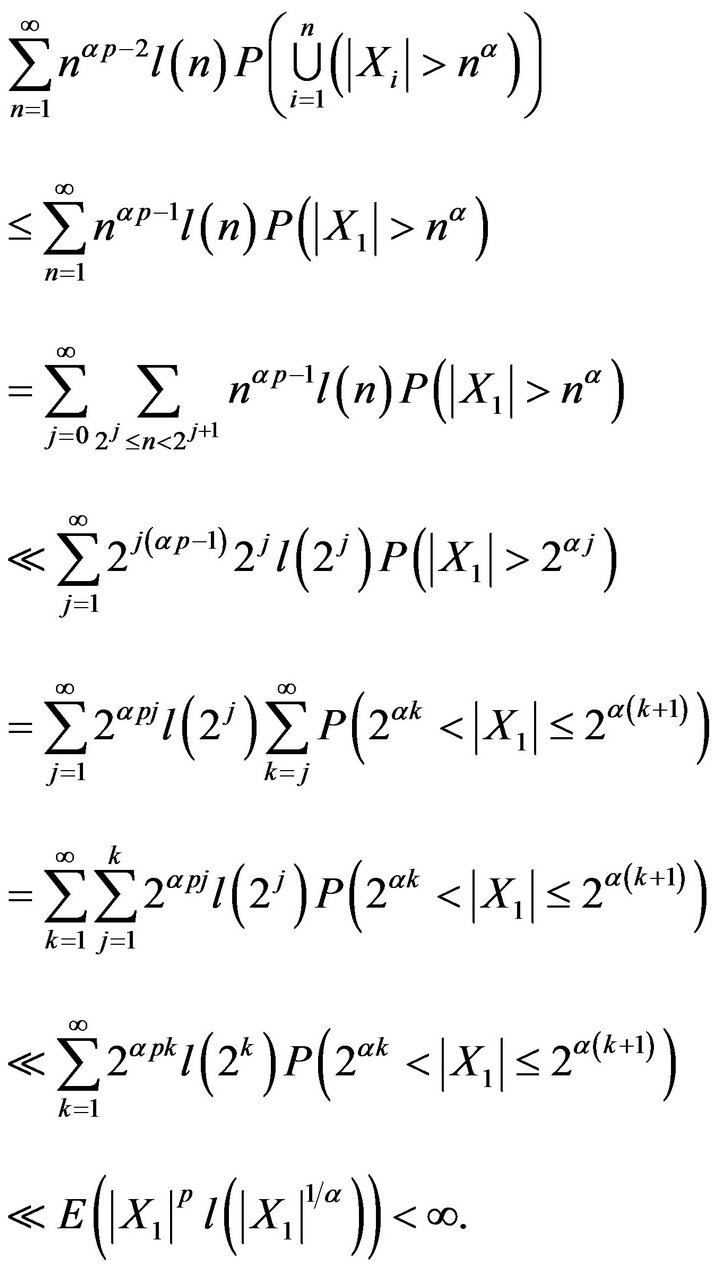
i.e., (2.7) holds.
By the Markov inequality, Lemma 1.2, Lemmas 2.1 (i), (iv), (2.1), and for each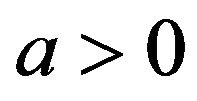 , the function
, the function 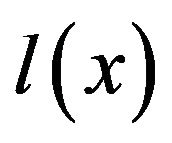 is bounded on the interval
is bounded on the interval ,
,

Hence, (2.8) holds.
Now we prove that (2.2)  (2.1). Obviously (2.2) implies
(2.1). Obviously (2.2) implies
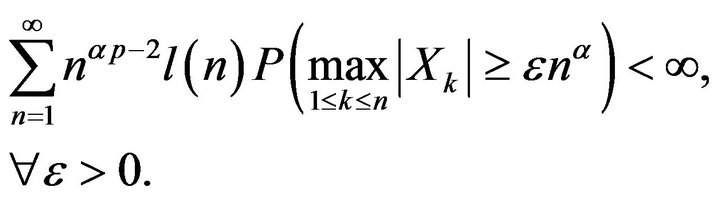 (2.9)
(2.9)
Noting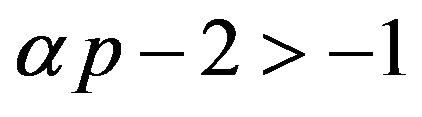 , by Lemma 2.1 (ii), we have
, by Lemma 2.1 (ii), we have

Thus,
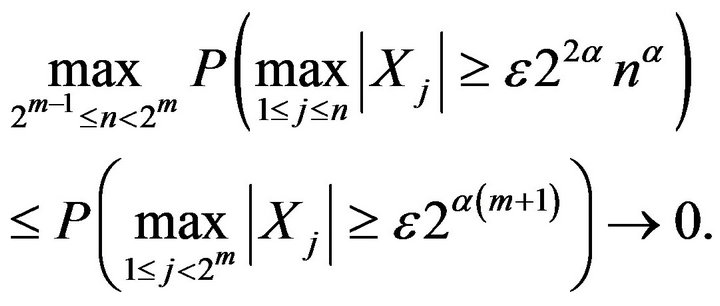
Therefore, for sufficiently large n,
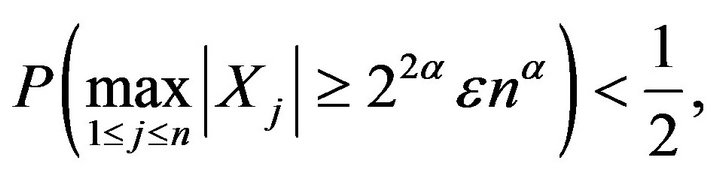
which, in conjunction with Lemma 1.2, gives
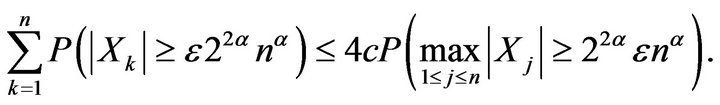
Putting this one into (2.9), we get furthermore
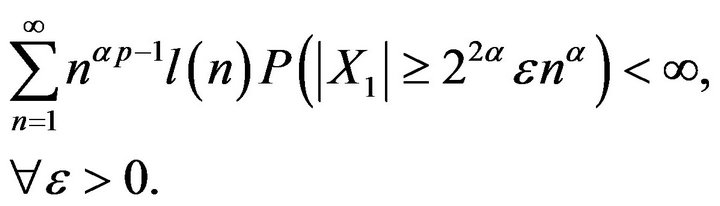
Thus, by Lemmas 2.1 (i), (iii),

This completes the proof of Theorem 2.1.
Proof of Theorem 2.2. (2.3)  (2.4). Let
(2.4). Let
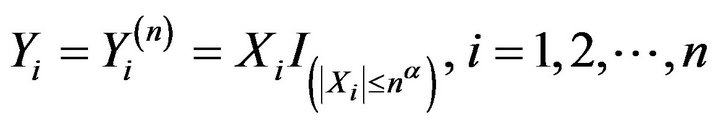 , the method of proof of Theorem 2.2 is similar to method used to prove the above Theorem 2.1. Only the method of prove of (2.5) is not the same. In what follows, we prove that (2.5) holds. Since
, the method of proof of Theorem 2.2 is similar to method used to prove the above Theorem 2.1. Only the method of prove of (2.5) is not the same. In what follows, we prove that (2.5) holds. Since  is a monotone non-decreasing function, we have
is a monotone non-decreasing function, we have
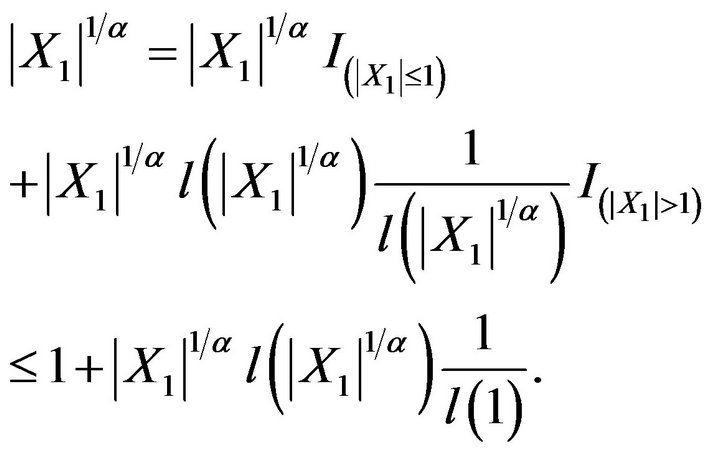
Hence, by (2.3),
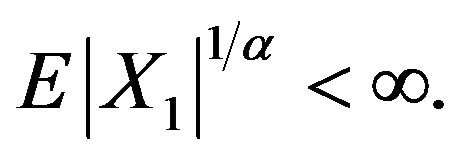 (2.10)
(2.10)
i) For , by
, by 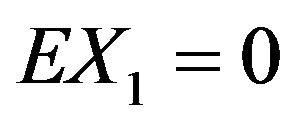 and (2.10),
and (2.10),
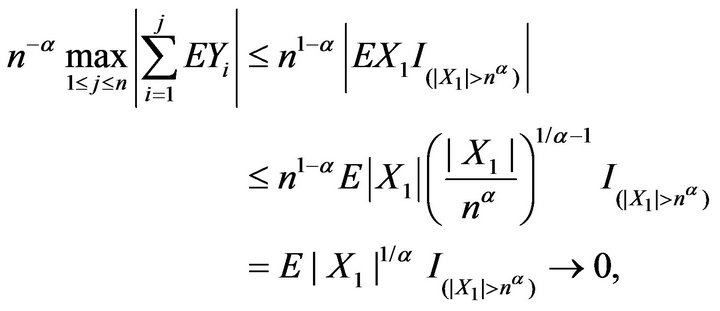
ii) For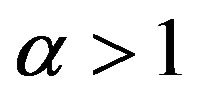 , i.e.,
, i.e.,  ,
,
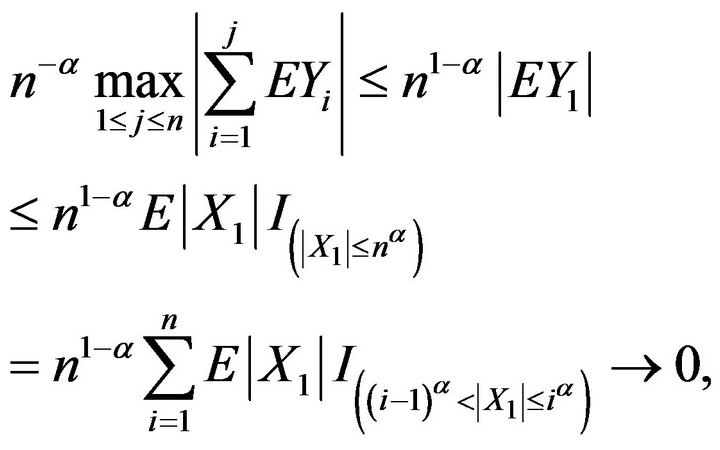
from the Kronecker lemma and

Hence (2.5) holds. The rest of the proof is similar to the corresponding part of the proof of Theorem 2.1, so we omit it.
3. Weak Law of Large Numbers
Theorem 3.1. Suppose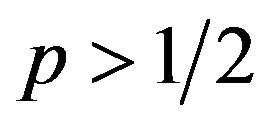 . Let
. Let 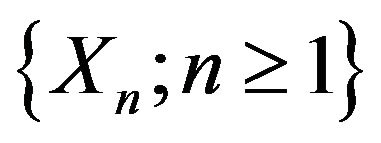 be a
be a  -mixing sequence of identically distributed random variables satisfying
-mixing sequence of identically distributed random variables satisfying
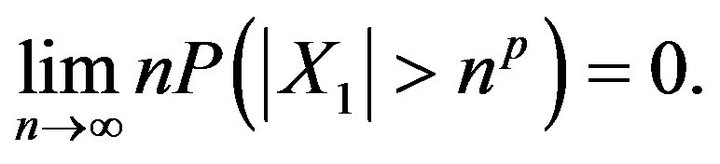 (3.1)
(3.1)
Then
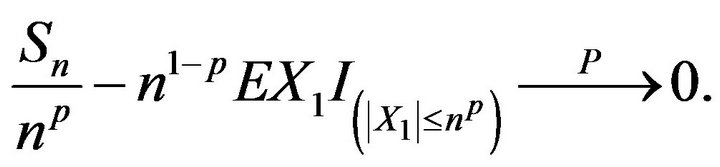 (3.2)
(3.2)
Remark 3.1. When 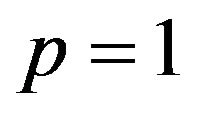 and
and 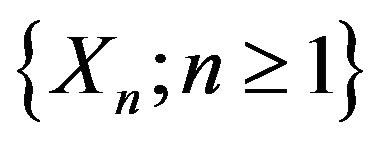 i.i.d., then Theorem 3.1 is the weak law of large numbers (WLLN) due to Feller [11]. So, Theorem 3.1 extends the sufficient part of the Feller’s WLLN from the i.i.d. case to a
i.i.d., then Theorem 3.1 is the weak law of large numbers (WLLN) due to Feller [11]. So, Theorem 3.1 extends the sufficient part of the Feller’s WLLN from the i.i.d. case to a 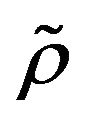 -mixing setting.
-mixing setting.
Proof of Theorem 3.1. Let 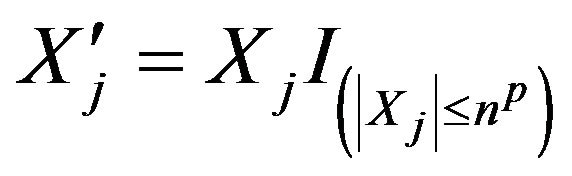 for
for 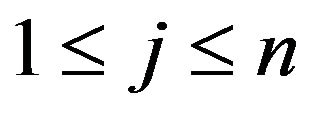 and
and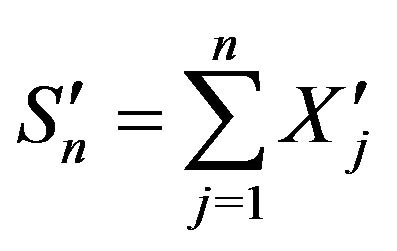 . Then, for each
. Then, for each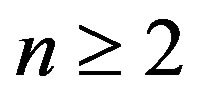 ,
,
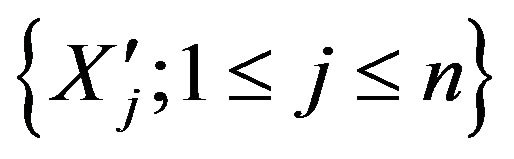 are
are 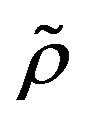 -mixing identically distributed random variables and for every
-mixing identically distributed random variables and for every ,
,
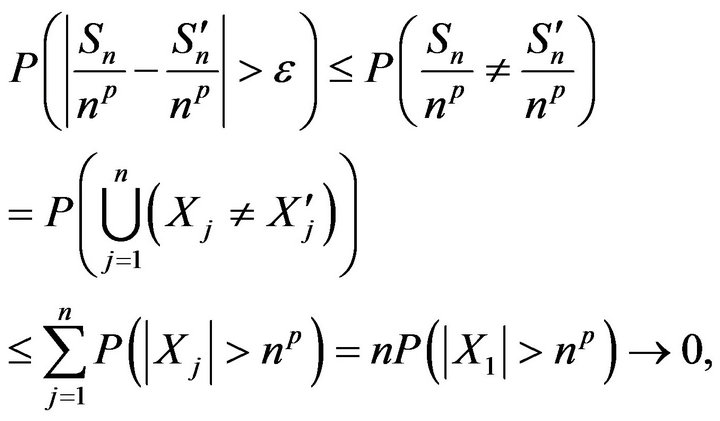
via (3.1). So that (3.1) entails

Thus, to prove (3.2) it suffices to verify that
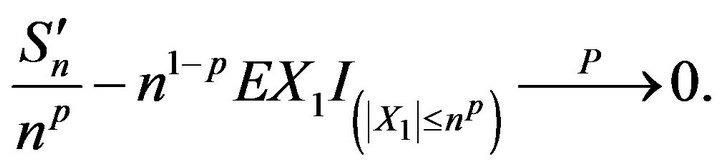 (3.3)
(3.3)
By (3.1) and the Toeplitz lemma,
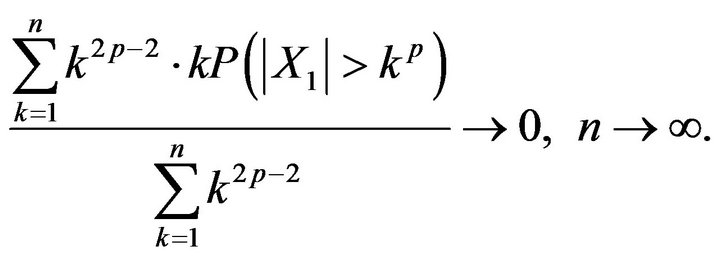
Thus, together with 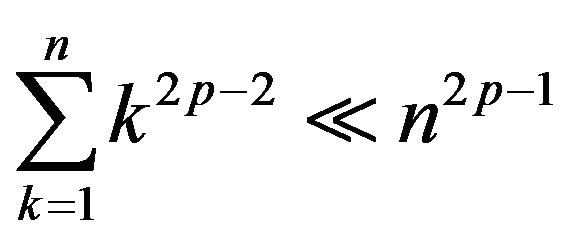 for
for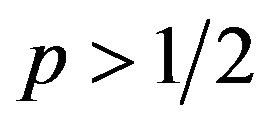 , we have
, we have

which, in conjunction with Lemma 1.1, yields for every ,
,

Thus
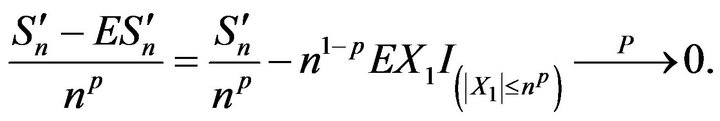
i.e. (3.3) holds.
4. Examples
In this section, we give two examples to show our Theorems.
Example 4.1. Let 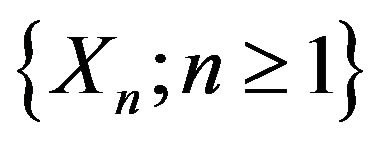 be a
be a  -mixing sequence of identically distributed random variables. Suppose
-mixing sequence of identically distributed random variables. Suppose 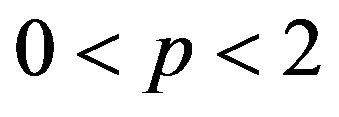 and
and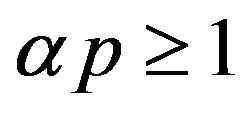 ; and if
; and if 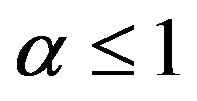 then suppose also that
then suppose also that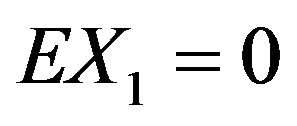 . Assume that
. Assume that 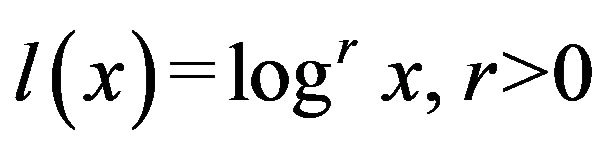 and
and  has a distribution with
has a distribution with
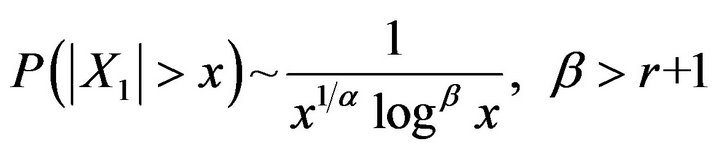 .
.
Is easy to verify that  satisfies the conditions of Theorems 2.1 and 2.2, and
satisfies the conditions of Theorems 2.1 and 2.2, and
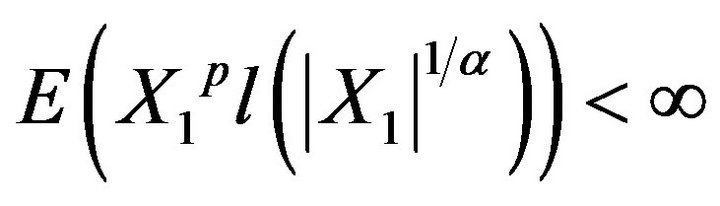 .
.
Thus, by Theorems 2.1 and 2.2,
 .
.
Example 4.2. Suppose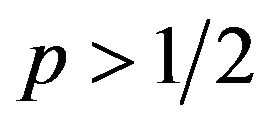 . Let
. Let 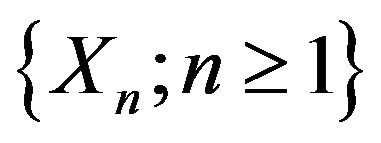 be a
be a  -mixing sequence of identically distributed random variables. Assume that
-mixing sequence of identically distributed random variables. Assume that 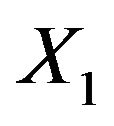 has a distribution with
has a distribution with
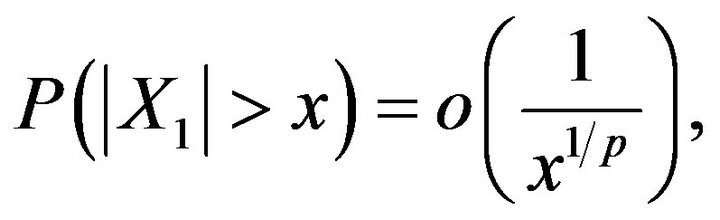
then obviously,
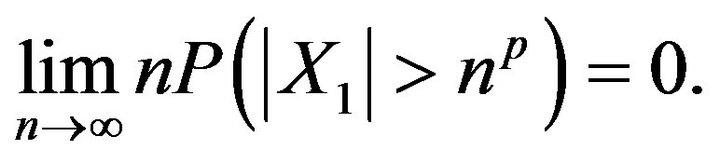
Thus, by Theorem 3.1,
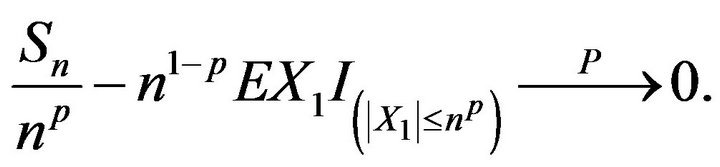
5. Acknowledgements
The work is supported by the National Natural Science Foundation of China (11061012), project supported by Program to Sponsor Teams for Innovation in the Construction of Talent Highlands in Guangxi Institutions of Higher Learning ([2011] 47), the Guangxi China Science Foundation (2012GXNSFAA053010), and the support program of Key Laboratory of Spatial Information and Geomatics (1103108-08).
REFERENCES
- W. Bryc and W. Smolenski, “Moment Conditions for Almost Sure Convergence of Weakly Correlated Random Variables,” Proceedings of the American Mathematical Society, Vol. 199, No. 2, 1993, pp. 629-635. doi:10.1090/S0002-9939-1993-1149969-7
- R. C. Bradley, “On the Spectral Density and Asymptotic Normality of Weakly Dependent Random Fields,” Journal of Theoretical Probability, Vol. 5, No. 2, 1992, pp. 355-373.
- S. C. Yang, “Some Moment Inequalities for Partial Sums of Random Variables and Their Applications,” Chinese Science Bulletin, Vol. 43, No. 17, 1998, pp. 1823-1827. doi:10.1007/BF02883381
- Q. Y. Wu and Y. Y. Jiang, “Some Strong Limit Theorems for
 -Mixing Sequences of Random Variables,” Statistics & Probability Letters, Vol. 78, No. 8, 2008, pp. 1017-1023.
-Mixing Sequences of Random Variables,” Statistics & Probability Letters, Vol. 78, No. 8, 2008, pp. 1017-1023. - Q. Y. Wu and Y. Y. Jiang, “Some Strong Limit Theorems for Weighted Product Sums of
 -Mixing Sequences of Random Variables,” Journal of Inequalities and Applications, 2009. doi:10.1155/2009/174768
-Mixing Sequences of Random Variables,” Journal of Inequalities and Applications, 2009. doi:10.1155/2009/174768 - Q. Y. Wu and Y. Y. Jiang, “Chover-Type Laws of the K-Iterated Logarithm for
 -Mixing Sequences of Random Variables,” Journal of Mathematical Analysis and Applications, Vol. 366, No. 2, 2010, pp. 435-443. doi: 10.1016/j.jmaa.2009.
-Mixing Sequences of Random Variables,” Journal of Mathematical Analysis and Applications, Vol. 366, No. 2, 2010, pp. 435-443. doi: 10.1016/j.jmaa.2009. - Q. Y. Wu, “Further Study Strong Consistency of Estimator in Linear Model for
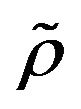 -Mixing Random Samples,” Journal of Systems Science and Complexity, Vol. 24, No. 5, 2011, pp. 969-980. doi:10.1007/s11424-011-8407-7
-Mixing Random Samples,” Journal of Systems Science and Complexity, Vol. 24, No. 5, 2011, pp. 969-980. doi:10.1007/s11424-011-8407-7 - M. Peligrad and A. Gut, “Almost-Sure Results for a Class of Dependent Random Variables,” Journal of Theoretical Probability, Vol. 12, No. 1, 1999, pp. 87-104.
- S. X. Gan, “Almost Sure Convergence for
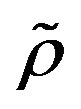 -Mixing Random Variable Sequences,” Statistics and Probability Letters, Vol. 67, 2004, pp. 289-298.
-Mixing Random Variable Sequences,” Statistics and Probability Letters, Vol. 67, 2004, pp. 289-298. - S. Utev and M. Peligrad, “Maximal Inequalities and an Invariance Principle for a Class of Weakly Dependent Random Variables,” Journal of Theoretical Probability, Vol. 16, No. 1, 2003, pp. 101-115. doi:10.1023/A:1022278404634
- W. Feller, “A Limit Theorem for Random Variables with Infinite Moments,” American Journal of Mathematics, Vol. 68, 1946, pp. 257-262.
- L. E. Baum and M. Katz, “Convergence Rates in the Law of Large Numbers,” Transactions of the American Mathematical Society, Vol. 120, No. 1, 1965, pp. 108-123.
- Z. D. Bai and C. Su, “The Complete Convergence for Partial Sums of iid Random Variables,” Science in China, Series A, Vol. 5, 1985, pp. 309-412.

