Open Journal of Statistics
Vol.2 No.1(2012), Article ID:17140,11 pages DOI:10.4236/ojs.2012.21004
Estimation under a Finite Mixture of Exponentiated Exponential Components Model and Balanced Square Error Loss
Department of Mathematics, Alexandria University, Alexandria, Egypt
Email: *dr_essak@hotmal.com, m.hussein.sci@hotmail.com
Received September 29, 2011; revised October 27, 2011; accepted November 12, 2011
Keywords: Finite Mixtures; Exponentiated Exponential Distribution; Maximum Likelihood Estimation; Bayes Estimation, Square Error and Balanced Square Error Loss Functions; Objective Prior
ABSTRACT
By exponentiating each of the components of a finite mixture of two exponential components model by a positive parameter, several shapes of hazard rate functions are obtained. Maximum likelihood and Bayes methods, based on square error loss function and objective prior, are used to obtain estimators based on balanced square error loss function for the parameters, survival and hazard rate functions of a mixture of two exponentiated exponential components model. Approximate interval estimators of the parameters of the model are obtained.
1. Introduction
The study of homogeneous populations was the main concern of statisticians along history. However, Newcomb [1] and Pearson [2] were two pioneers who approached heterogeneous populations with 'finite mixture distributions’.
With the advent of computing facilities, the study of heterogeneous populations, which is the case with many real World populations (see Titterington et al. [3]), attracted the interest of several researchers during the last sixty years. Monographs and books by Everitt and Hand [4], Titterington et al. [3], McLachlan and Basford [5], Lindsay [6] and McLachlan and Peel [7], collected and organized the research done in this period, analyzed data and gave examples of possible practical applications in different areas. Reliability and hazard based on finite mixture models were surveyed by AL-Hussaini and Sultan [8].
In this paper, concentration will be on the study of a finite mixture of two exponentiated exponential components. Due to the exponentiation of each component by a positive parameter, the model is so flexible that it shows different shapes of hazard rate function.
Maximum likelihood estimates (MLEs) and Bayes estimates (BEs), using square error loss (SEL) function are obtained and used in finding the estimates of the parameters, survival function (SF) and hazard rate function (HRF) using the balanced square error loss (BSEL) function.
Approximate interval estimators of the parameters are obtained by first finding the approximate Fisher information matrix.
The cumulative distribution function (CDF), denoted by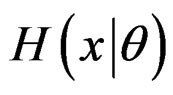 , of a finite mixture of k components, denoted by
, of a finite mixture of k components, denoted by , is given by
, is given by
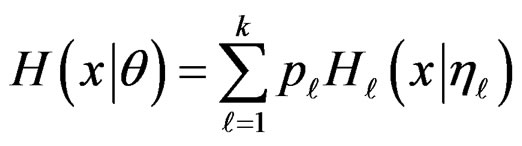 , (1)
, (1)
where, for , the mixing proportions
, the mixing proportions 
and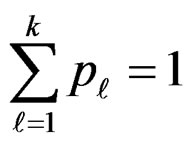 . The vector of parameters
. The vector of parameters
 , where
, where  is a parameter space.
is a parameter space.
The case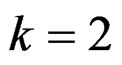 , in (1), is of practical importance and so,we shall restrict our study to this case. In such case, the population consists of two sub-populations, mixed with proportions p and
, in (1), is of practical importance and so,we shall restrict our study to this case. In such case, the population consists of two sub-populations, mixed with proportions p and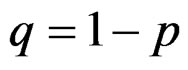 . We shall write the CDF of a mixture of two components as
. We shall write the CDF of a mixture of two components as
 , (2)
, (2)
where, for 
 is the CDF of the
is the CDF of the  sub-population,
sub-population,  and
and .
.
AL-Hussaini and Ahmad [9] obtained the information matrix for a mixture of two Inverse Gaussian components. AL-Hussaini and Abd-El-Hakim ([10-12]) studied the failure rate of a finite mixture of two components, one of which is Inverse Gaussian and the other is Weibull. They estimated the parameters of such model and studied the efficiency of schemes of sampling. AL-Hussaini [13] predicted future observables from a mixture of two exponential components. AL-Hussaini [14] obtained Bayesian predictive density function when the population density is a mixture of general components. Other references on finite mixtures may be found in AL-Hussaini and Sultan [8].
In this paper, the components are assumed to be exponentiated exponential whose CDFs are of the form
 , (3)
, (3)
where  So that the corresponding probability density function (PDF) components take, for
So that the corresponding probability density function (PDF) components take, for , the form
, the form
 . (4)
. (4)
The PDF, SF and HRF, of the mixture (2), denoted by 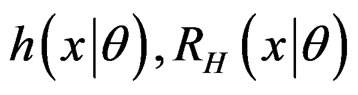 and
and 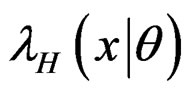 are given by
are given by
 , (5)
, (5)
 (6)
(6)

 (7)
(7)
where , and for
, and for ,
,
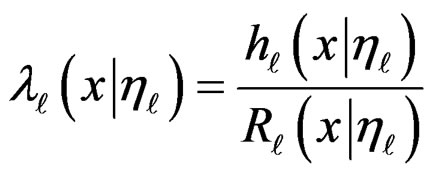
 . (8)
. (8)
In (5)-(8),  and
and  shall be given by (3) and (4), respectively, so that
shall be given by (3) and (4), respectively, so that 
2. Hazard Rate Function of the Mixture
It is well-known that the exponential distribution has a constant HRF on the positive half of the real line. A finite mixture of two exponential components has a decreasing hazard rate function (DHRF) on the positive half of the real line. See, for example, AL-Hussaini and Sultan [8]. If each of the exponential components is exponentiated by a positive parameter, more flexible model is obtained in that several shapes of the HRF of the mixture are obtained. Figure 1 shows six different shapes of CDFs and their corresponding HRFs of the vector of parameters. Examples of such shapes are given as follows:






3. Point Estimation Using Balanced Square Error Loss Function
It is well-known that the Bayes estimator  of a function
of a function  of a vector of parameters
of a vector of parameters  under SEL is given by
under SEL is given by
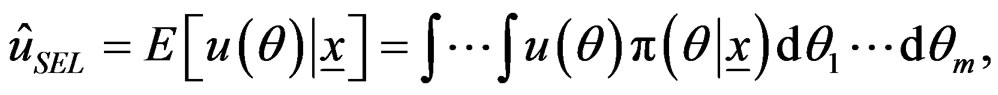 (9)
(9)
where the integrals are taken over the m-dimensional space and  is the posterior PDF of
is the posterior PDF of  give
give .
.
The SEL function has probably been the most popular loss function used in literature. The symmetric nature of SEL function gives equal weight to overand under-estimation of the parameters under consideration. However, in life-testing, over-estimation may be more serious than under-estimation or vice-versa. Consequently, research has been directed towards asymmetric loss functions. Varian [15] suggested the use of linear exponential (LINEX) loss functions. Thompson and Basu [16] suggested the use of quadratic exponential (QUADREX) loss function. Ahmadi et al. [17] suggested the use of the so called balanced loss function (BLF), which was originated by Zellner [18], to be of the form
 (10)
(10)
where  is am arbitrary loss function,
is am arbitrary loss function,  is a chosen “target” estimator of
is a chosen “target” estimator of 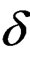 and the weight
and the weight 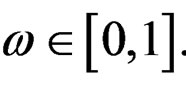
The BLF (10) specializes to various choices of loss functions such as the absolute error loss, entropy, LINEX and generalizes SEL functions.
If  is substituted in (10), we obtain the balanced square error loss (BSEL) function, given by
is substituted in (10), we obtain the balanced square error loss (BSEL) function, given by


The estimator  of a function
of a function , using BSEL may be given by
, using BSEL may be given by
 , (11)
, (11)
where  is the MLE of
is the MLE of  and
and  its Bayes
its Bayes
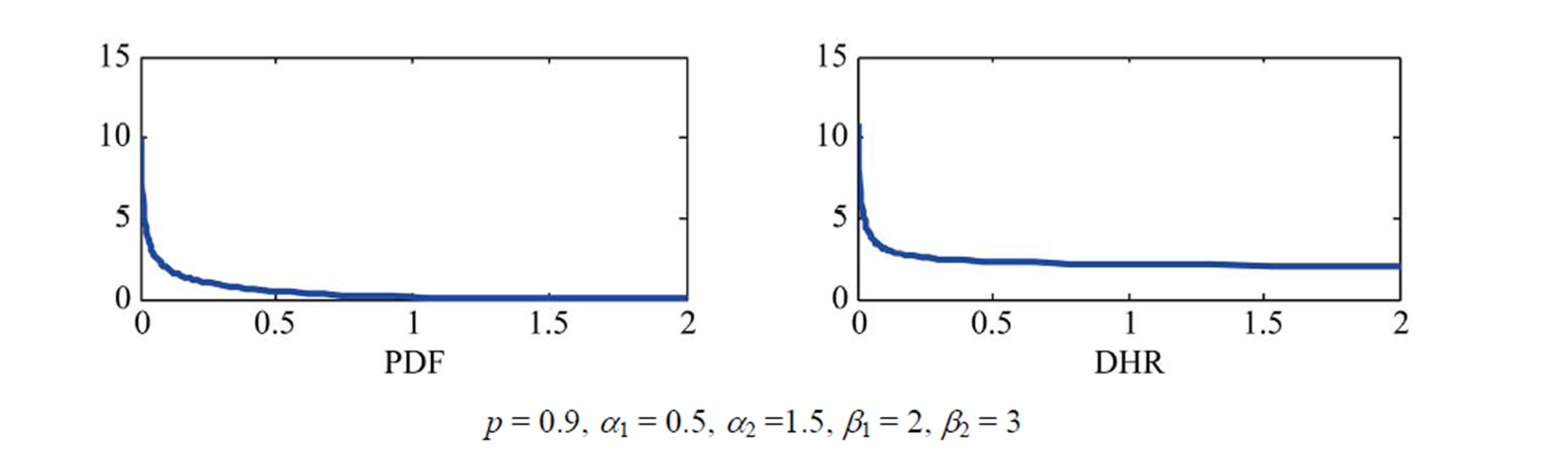





Figure 1. Different shapes of PDFs and their corresponding HRFs. D = decreasing, I = increasing, BT = bathtub, UBT = upside down bathtub, DID = decreasing-increasing-decreasing, IDI = increasing-decreasing-increasing.
estimator using SEL function. The estimator of a function, using BSEL is actually a mixture of the MLE of the function and the BE, using SEL. Other estimators, such as the least squares estimator may replace the MLE. Also, a LINEX or QUADREX loss function could be used for . Having obtained the MLE and BE based on SEL, the estimates based on BSEL function are given, from (11), by
. Having obtained the MLE and BE based on SEL, the estimates based on BSEL function are given, from (11), by
 (12)
(12)
Suppose that r units have failed during the interval :
: 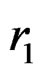 units from the first sub-population and
units from the first sub-population and  units from the second such that
units from the second such that  and n – r units , which cannot be identified as to sub-population, are still functioning. Let, for
and n – r units , which cannot be identified as to sub-population, are still functioning. Let, for  and
and 
 denote the failure time of the ith unit belonging to the
denote the failure time of the ith unit belonging to the 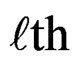 sub-population and that
sub-population and that . The likelihood function (LF) is given by Mendenhall and Hader [19], as
. The likelihood function (LF) is given by Mendenhall and Hader [19], as
 (13)
(13)
where  is the vector of parameters involved and
is the vector of parameters involved and ,
, . By substituting
. By substituting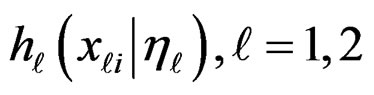 , given by (4), in (13), we obtain
, given by (4), in (13), we obtain
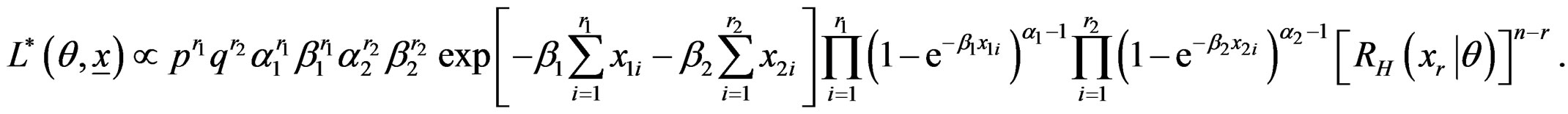 (14)
(14)
3.1. Maximum Likelihood Estimation
The log-LF is given by
 (15)
(15)
The MLEs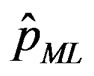 ,
,  ,
, 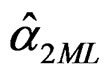 ,
,  ,
,  , of the five parameters are obtained by solving the following system of likelihood equations
, of the five parameters are obtained by solving the following system of likelihood equations





where
 .
.
The invariance property of MLEs enables us to obtain the MLEs  and
and  by replacing the parameters by their MLEs in
by replacing the parameters by their MLEs in  and
and .
.
Remarks 1) If n = r (complete sample case),
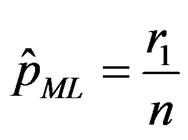 ,
,

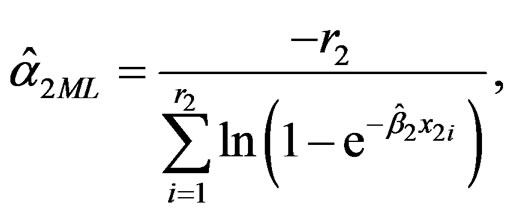
 ,
,
 .
.
2) It can be numerically shown that the vector of parameters , satisfying the likelihood equations actually maximizes the LF (14). This is done by applying Theorem (7-9) on p. 152 of Apostol [20].
, satisfying the likelihood equations actually maximizes the LF (14). This is done by applying Theorem (7-9) on p. 152 of Apostol [20].
3) The parameters of the components are assumed to be distinct, so that the mixture is identifiable. For the concept of identifiability of finite mixtures and examples, see Everitt and Hand [4], AL-Hussainiand Ahmad [21] and Ahmad and AL-Hussaini [22].
3.2. Bayes Estimation Using SEL Function
Suppose that an objective (non-informative) prior is used, in which p,  ,
,  ,
,  ,
,  are independent and that p-Uniform on
are independent and that p-Uniform on , so that the prior PDF is given by
, so that the prior PDF is given by
 . (16)
. (16)
The following theorem gives expressions for the Bayes estimators using the SEL function.
Theorem The Bayes estimators of the parameters, SF and HRF, assuming that the prior belief of the expeimenter has PDF (16), are given by

where
 (17)
(17)
 (18)
(18)
 (19)
(19)
 (20)
(20)
 (21)
(21)
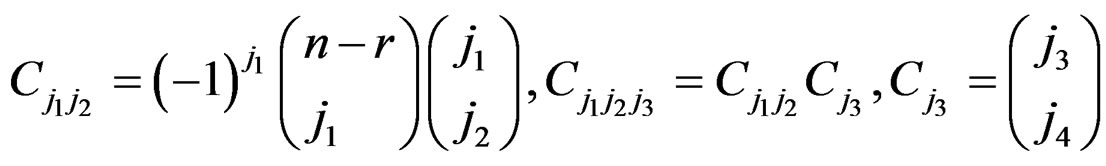 ,
,
 is the standard beta function,
is the standard beta function,

 , (22)
, (22)
 , (23)
, (23)
 , (24)
, (24)
 , (25)
, (25)
 , (26)
, (26)
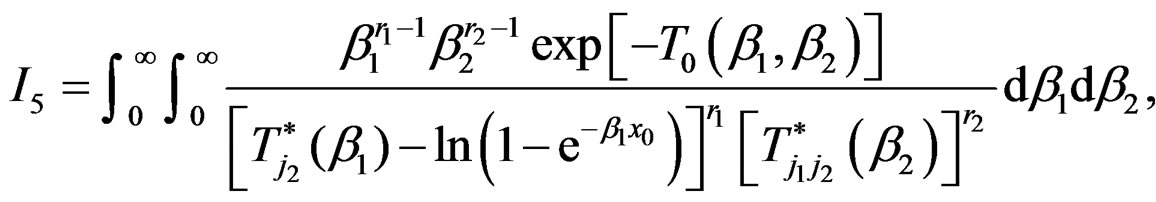 (27)
(27)
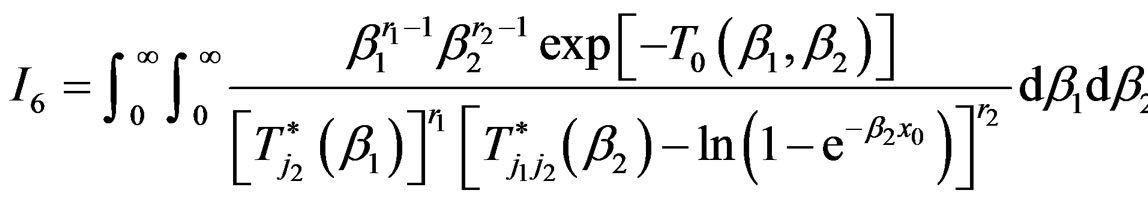 , (28)
, (28)
 , (29)
, (29)
 , (30)
, (30)
 (31)
(31)
 (32)
(32)
 (33)
(33)
The proof of the theorem is given in Appendix 1.
4. Approximate Confidence Intervals
Let . The observed Fisher information matrix F (see Nelson [23]), for the MLEs of the parameters is the 5 × 5 symmetric matrix of the negative second partial derivatives of log-LF (15) with respect to the parameters. That is
. The observed Fisher information matrix F (see Nelson [23]), for the MLEs of the parameters is the 5 × 5 symmetric matrix of the negative second partial derivatives of log-LF (15) with respect to the parameters. That is
 , evaluated at the vector of MLEs
, evaluated at the vector of MLEs .
.
The second partial derivatives are given in Appendix 2.
The inverse of F is the local estimate V of the asymptotic variance-covariance matrix of
 . That is,
. That is,
 , (34)
, (34)
where .
.
The observed Fisher information matrix enables us to construct confidence intervals for the parameters based on the limiting normal distribution. Following the general asymptotic theory of MLEs, the sampling distribution of , can be approximated by a standard normal distribution, where
, can be approximated by a standard normal distribution, where  , the ith diagonal element of the matrix V, given by (34).
, the ith diagonal element of the matrix V, given by (34).
An approximate two-sided 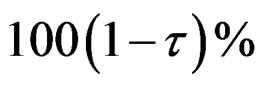 confidence interval for
confidence interval for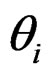 , is given for
, is given for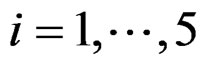 , by
, by
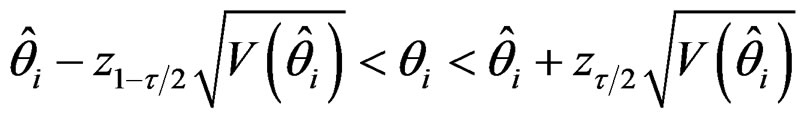 , (35)
, (35)
where  is the percentile of the standard normal distribution with right—tale probability of c.
is the percentile of the standard normal distribution with right—tale probability of c.
5. Numerical Example
5.1. Point Estimation of the Parameters, SF and HRF
A sample is generated from the mixture in such a way that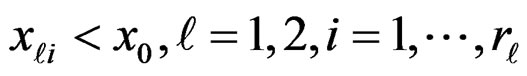 . We generate 100 samples of size n = 50 each, from a finite mixture of two exponentiated exponential components, whose PDF is given by (5) and (4), as follows:
. We generate 100 samples of size n = 50 each, from a finite mixture of two exponentiated exponential components, whose PDF is given by (5) and (4), as follows:
1) Generate  and
and  from Uniform (0,l) distribution.
from Uniform (0,l) distribution.
2) For given values of p, a1, a2, b1, b2, generate x according to the expression:

An observation  belongs to sub-population 1, if
belongs to sub-population 1, if  and to sub-population 2, if
and to sub-population 2, if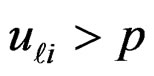 , where the sample is generated from the mixture in such a way that
, where the sample is generated from the mixture in such a way that .
.
3) Repeat until you get a sample of size n.
The observations are ordered and only the first r = 45 (90% of n) out of the n = 50 observations are assumed to be known. Now we have  observations from the first component of the mixture and
observations from the first component of the mixture and  observations from the second component (
observations from the second component ( ).
).
The value of  is chosen to be equal to 1.
is chosen to be equal to 1.
The estimates of p, a1, a2, b1, b2, 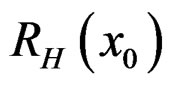 and
and  and absolute biases are computed by using the ML and Bayes methods. The Bayes estimates are obtained under SEL function. An estimator of a function, using BSEL, is actually a mixture (w = 0.2, 0.4, 0.6, 0.8) of the MLE of the function and the BE, using SEL.
and absolute biases are computed by using the ML and Bayes methods. The Bayes estimates are obtained under SEL function. An estimator of a function, using BSEL, is actually a mixture (w = 0.2, 0.4, 0.6, 0.8) of the MLE of the function and the BE, using SEL.
The MLEs are computed using the built-in MATLAB® function “ga” to find the maximum of the log-LF (15) using the genetic algorithm. This is better than solving the system of five likelihood equations in the five unknowns, by using some iteration scheme. Neverthless,

Table 1. Estimates of the parameters, SF and HRF under BSEL function and absolute biases.
the system is needed for the computations of the asymptotic variance-covariance matrix.
The (arbitrarily) chosen actual population values are p = 0.4, a1 = 2, a2 = 3, b1 = 2, and b2 = 3. For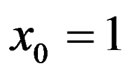 , the actual values for
, the actual values for  and
and  are given, respectively, by 0.1862 and 2.3096.
are given, respectively, by 0.1862 and 2.3096.
The estimates of the parameters, SF and HRF under the BSEL function are given in Table 1, for different weights . It may be noticed that when
. It may be noticed that when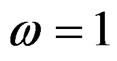 , we obtain the MLEs while the case
, we obtain the MLEs while the case , yields the Bayes estimates under SEL(B-SEL) function.
, yields the Bayes estimates under SEL(B-SEL) function.
5.2. Interval Estimation of the Parameters
The asymptotic variance-covariance matrix (34), based on the generated data, is found to be

So that the asymptotic variances of the estimators of the parameters are given by:

It then follows that the approximate 95% confidence intervals of the parameters p,  ,
,  ,
,  and
and , given by (35), are given, respectively, by: (0.271 < p < 0.561), (0.5287 < a1 < 4.7599), (1.3832 < a2 < 5.3226), (0.9294 < b1 < 4.18) and (1.8039 < b2 < 4.56).
, given by (35), are given, respectively, by: (0.271 < p < 0.561), (0.5287 < a1 < 4.7599), (1.3832 < a2 < 5.3226), (0.9294 < b1 < 4.18) and (1.8039 < b2 < 4.56).
6. Concluding Remarks
In this article, we have considered point and interval estimation. Point estimation, of the parameters of a finite mixture of two exponentiated exponential components, SF and HRF is based on BLEF which is a weighted average of two losses: one of which reflects precision of estimation and the other reflects goodness-of-fit. This asymmetric loss function may be considered as a compromise between Bayesian and non-Bayesian estimates. We have also estimated the parameters of the mixture by obtaining the asymptotic variance-covariance matrix and hence the approximate confidence intervals.
REFERENCES
- S. Newcomb, “A Generalized Theory of the Combination of Observations So as to Obtain the Best Result,” American Journal of Mathematics, Vol. 8, No. 4, 1886, pp. 343- 366. doi:10.2307/2369392
- K. Pearson, “Contributions to the Mathematical Theory of Evolution,” Philosophical Transactions A, Vol. 185, 1894, pp. 71-110.
- D. M. Titterington, A. F. M. Smith and U. E. Makov, “Statistical Analysis of Finite Mixture Distributions,” Wiley, New York, 1985.
- B. S. Everitt and D. J. Hand, “Finite Mixture Distributions,” Chapman & Hall, London, 1981. doi:10.1007/978-94-009-5897-5
- G. J. McLachlan and K. E. Basford, “Mixture Models: Applications to Clustering,” Macel Dekker, New York, 1988.
- B. G. Lindsay, “Mixture Models: Theory, Geometry and Applications,” Institute of Mathematical Statistics, Hayward, 1995.
- G. J. McLachlan and D. Peel, “Finite Mixture Models,” Wiley, New York, 2000. doi:10.1002/0471721182
- E. K. AL-Hussaini and K. S. Sultan, “Reliability and Hazard Based on Finite Mixture Models,” In: N. Balakrishnan and C. R. Rao, Eds., Advances in Reliability, Vol. 20, Elsevier, Amsterdam, 2001.
- E. K. AL-Hussaini and K. E. Ahmad, “Information Matrix for a Mixture of Two Inverse Gaussian Distributions,” Communications in Statistics—Simulation and Computation, Vol. 13, No. 6, 1984, pp. 785-800. doi:10.1080/03610918408812415
- K. E. AL-Hussaini and N. S. Abd-El-Hakim, “Failure Rate of the Inverse Gaussian-Weibull Model,” Annals of the Institute of Statistical Mathematics, Vol. 41, No. 3, 1989, pp. 617-622. doi:10.1007/BF00050672
- E. K. AL-Hussaini and N. S. Abd-El-Hakim, “Estimation of Parameters of the Inverse Gaussian-Weibull,” Communications in Statistics—Theory and Methods, Vol. 19, No. 5, 1990, pp. 1607-1622. doi:10.1080/03610929008830280
- E. K. AL-Hussaini and N. S. Abd-El-Hakim, “Efficiency of Schemes of Sampling from the Inverse Gaussian-Weibull Mixture Model,” Communications in Statistics— Theory and Methods, Vol. 21, No. 11, 1992, pp. 3143- 3169. doi:10.1080/03610929208830967
- E. K. AL-Hussaini, “Bayesian Prediction under a Mixture of Two Exponential Components Model Based on Type 1 Censoring,” Journal of Applied Statistical Science, Vol. 8, 1999, pp. 173-185.
- E. K. AL-Hussaini, “Bayesian Predictive Density of Order Statistics Based on Finite Mixture Models,” Journal of Statistical Planning and Inference, Vol. 113, No. 1, 2003, pp. 15-24. doi:10.1016/S0378-3758(01)00297-X
- H. Varian, “A Bayesian Approach to Real Estate Assessment,” In: S. E. Fienberg and A. Zellner, Eds., Studies in Bayesian Econometrics and Statistics, North Holland, Amsterdam, 1975.
- R. D. Thompson and A. P. Basu, “Asymptotic Loss Function for Estimating System Reliability,” In: D. A. Berry, K. M. Chaloner and J. K. Geweke, Eds., Bayesian Analysis in Statistics and Econometrics, Wiley, New York, 1996.
- J. Ahmadi, M. J. Jozani, E. Marchand and A. Parsian, “Bayes Estimation Based on k-Record Data from a General Class of Distributions under Balanced Type Loss Functions,” Journal of Statistical Planning and Inference, Vol. 139, No. 3, 2009, pp. 1180-1189. doi:10.1016/j.jspi.2008.07.008
- A. Zellner, “Bayesian and Non-Bayesian Estimation Using Balanced Loss Functions,” In: S. S. Gupta and J. O. Burger, Eds., Statistical Decision Theory and Related Topics V, Springer-Verlag, New York, pp. 377-390.
- W. Mendenhall and R. J. Hader, “Estimation of Parameters of Mixed Exponentially Distributed Failure Time Distributions from Censored Life Test Data,” Biometrika, Vol. 45, 1958, pp. 504-520.
- T. M. Apostol, “Mathematical Analysis,” Addison Wesley, Reading, 1957.
- E. K. AL-Hussaini and K. E. Ahmad, “On the Identifiability of Finite Mixtures of Distributions,” IEEE Transaction on Information Theory, Vol.27, No. 5, 1981, pp. 664-668. doi:10.1109/TIT.1981.1056389
- K. E. Ahmad and E. K. AL-Hussaini, “Remarks on the Non-Identifiability of Finite Mixtures,” Annals of the Institute of Statistical Mathematics, Vol. 34, No. 1, 1982, pp. 543-544. doi:10.1007/BF02481052
- W. Nelson, “Lifetime Data Analysis,” Wiley, New York, 1990.
Appendix 1
Proof of the Theorem By expanding the last term in LF (14), using the binomial expansion, it can be seen that

where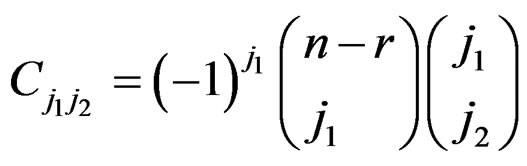 .
.
So that LF (14) can be written in the form
 where
where ,
,  ,
,  are given by (31). Suppose that the prior PDF is as in (16). It then follows that the posterior PDF is given by
are given by (31). Suppose that the prior PDF is as in (16). It then follows that the posterior PDF is given by
 (34)
(34)
where 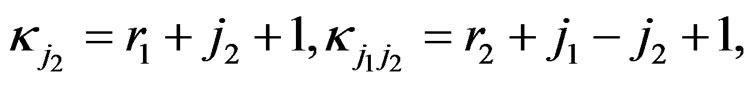
 and
and  are given by (32). The normalizing constant A is given by
are given by (32). The normalizing constant A is given by
 where
where  is given by (17), in which
is given by (17), in which  is given by (22).
is given by (22).
Applying (9) when
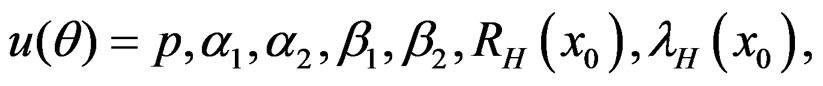
their Bayes estimates using SEL function are given by
 ,
,  is given in (17).
is given in (17).
 ,
,  is given in (18), in which
is given in (18), in which 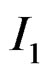 is given by (23).
is given by (23). ,
,  is given in (18), in which
is given in (18), in which  is given by (24).
is given by (24).
 ,
,  is given in (19), in which
is given in (19), in which  is given by (25).
is given by (25).
 ,
,  is given in (19), in which
is given in (19), in which  is given by (26).
is given by (26).
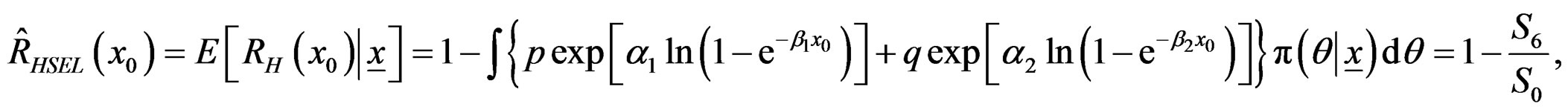
 is given in (20), in which
is given in (20), in which  is given by (27) and
is given by (27) and  by (28).
by (28).

where
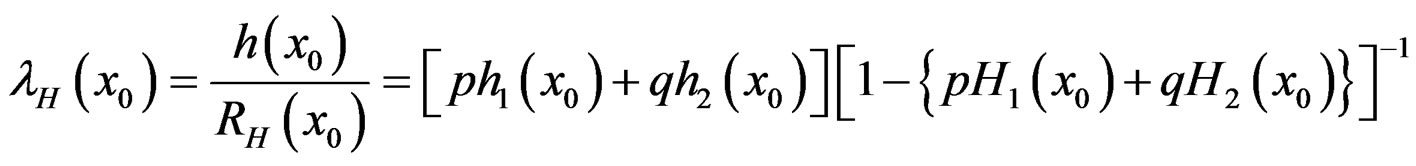 .
.
Since p ≤ 1, then

so that
 where
where . It then follows that
. It then follows that
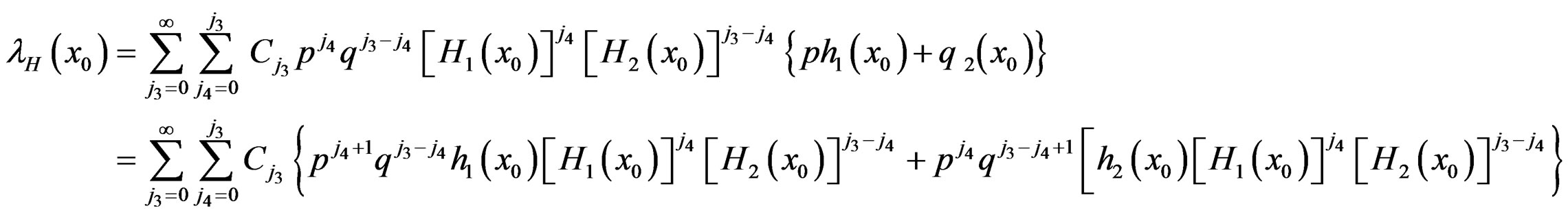
By substituting, for , and using
, and using  given by (34), it can be shown that
given by (34), it can be shown that
 (35)
(35)
where 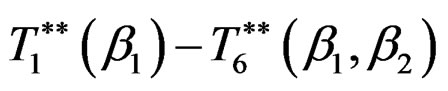 are given by (33). By integrating both sides of (35) with respect to the five parameters, we obtain
are given by (33). By integrating both sides of (35) with respect to the five parameters, we obtain 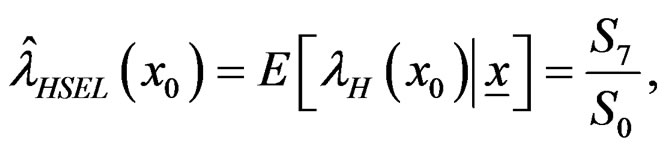
where S7 is given by (21), in which I7 is given by (29)
and I8 by (30).
Appendix 2
Second Partial Derivatives of the Log-likelihood Function
 ,
,
 ,
,
 ,
,
 ,
,
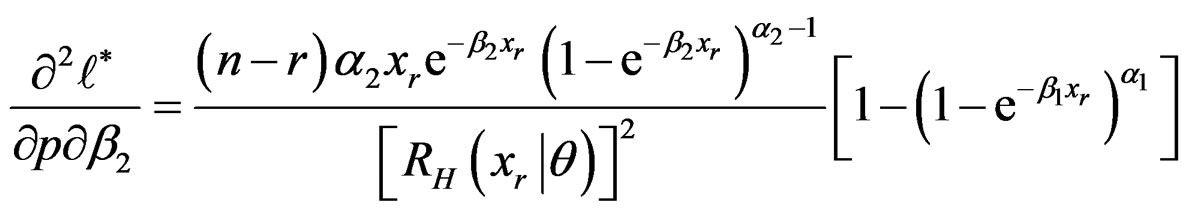 ,
,
 ,
,
 ,
,
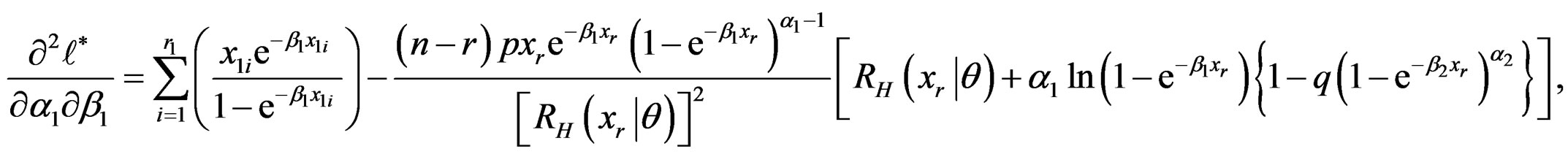
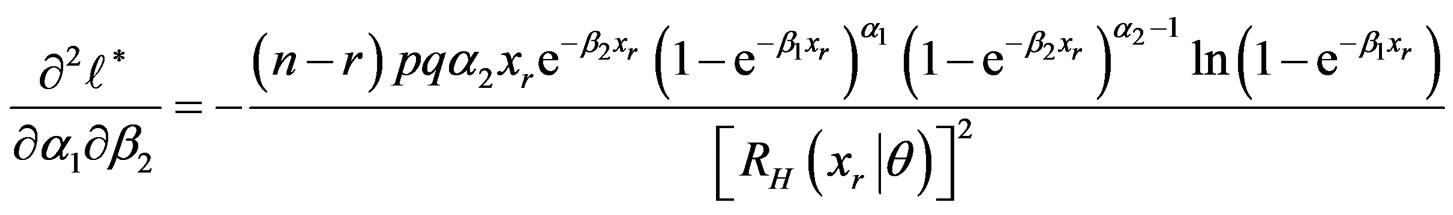 ,
,
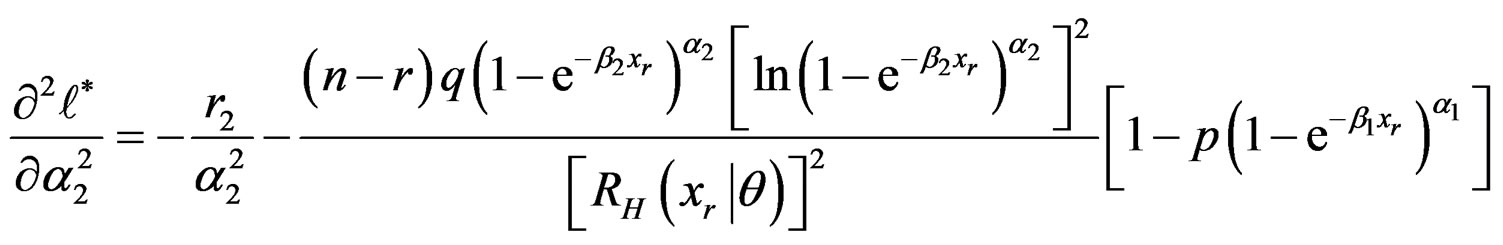 ,
,
 ,
,
 ,
,

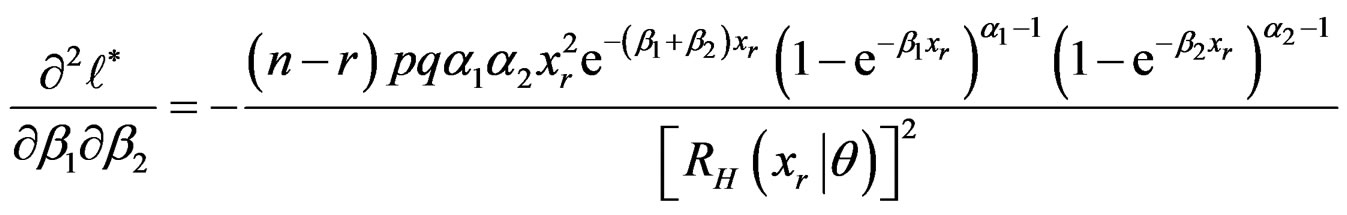 ,
,

NOTES
*Corresponding author.

