Abstract

In the present paper as estimation of unknown pdf derivative of a spline function is suggested. It is studied its some statistical properties which are used to approximate maximal deviation of the spline estimation from pdf with maximum of nonstationary gaussian process.

1. Introduction

The construction of a confidence interval for unknown probability density function (pdf) trough histogram for the first time has been suggested by Smirnov [1]. Bikel and Rosenblatt [2], Rosenblatt [3] have considered analogues problem using of Parsen-Rosenblatt’s estimation. The problem of construction of a confidence interval for unknown pdf trough spline-function was studied by Muminov and Khashimov [4]. Recently for unknown multidimensional distribution density function the kernel estimation is constructed and similar problem is studied by Muminov [5,6].

Several authors have considered the rate of convergence of the distribution of the maximum of difference between Parsen-Rosenblat’s estimator and unknown pdf, see, for example, Konakov and Piterbarg [7-9]. Nevertheless there is no such kind of result for the spline-estimators. The results obtained in this work help to approximate the deviation of spline estimation of unknown density by Gaussian process.

It should be noted that in the works of Lii and Rosenblatt [10], Muminov [11] asymptotical unbiasedness and strong state of the spline estimation are proved. Importance of spline-estimation and its application in statistics are given in the works [5,12].

The paper is organized as follows. In Sec. 2 the spline estimation is constructed and some auxiliary results are stated, and also the main theorem is given. The main theorem is proved in Sec. 3.

2. Results

Let 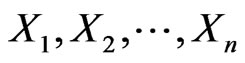be independent identical distributed random variables (r.v.) with pdf 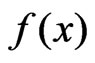and let 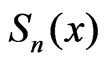be the cubic spline-function which do interpolation of 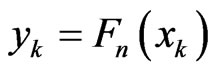at the points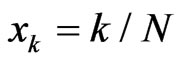, where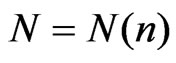, 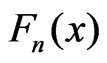is the epirical distribution function of the sample. Theboundary condition for are, ,.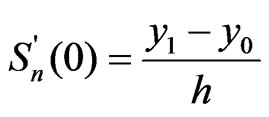

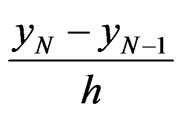
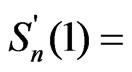Then the derivative of spline-function is as follows, see Lii [13]

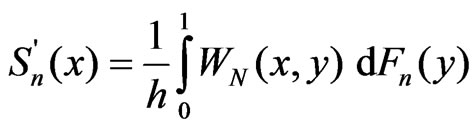
where, , , ,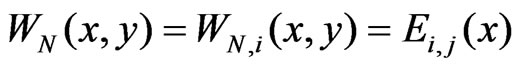

,

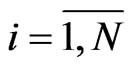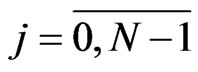
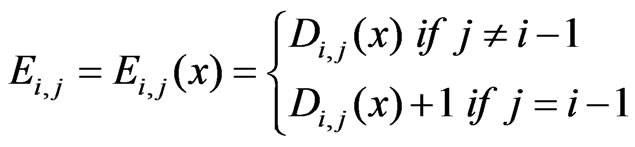
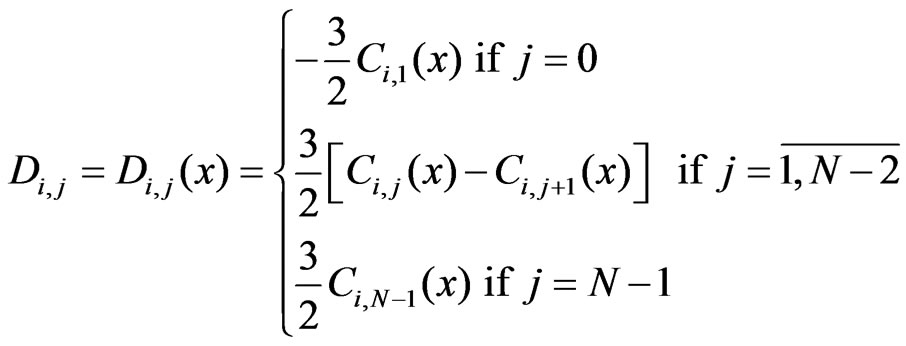
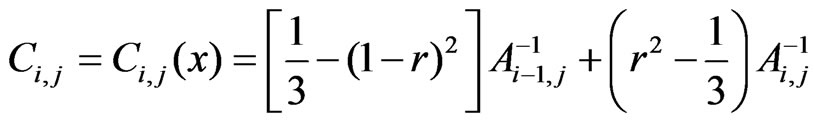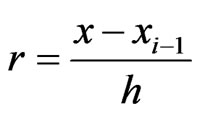
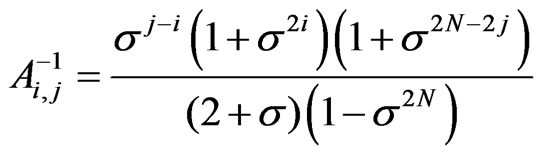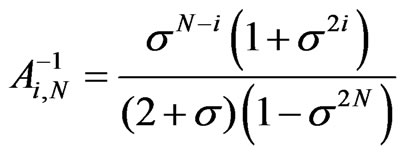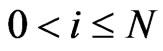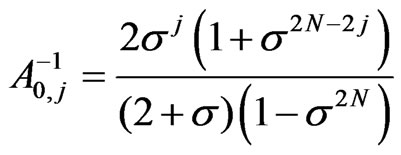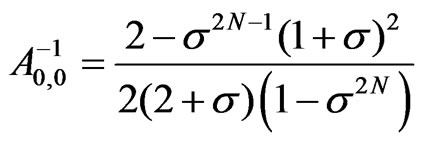
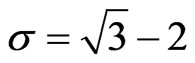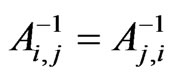, for, , for, , for, ,

, ,for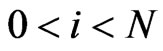, and 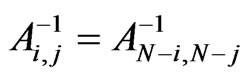for the other values of I, j,.

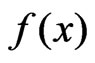We take the statistic as estimator of pdf. We define r.v. 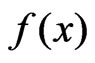by the following equality

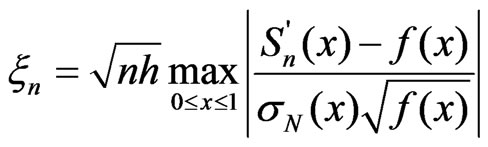where.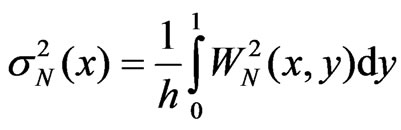

R.v. 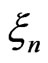is interesting with point of view of solution of the following problems:

1) to find a confidential strip for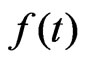, 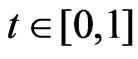on given coefficient of trust;

2) to construct criterion for test of null hypothesis 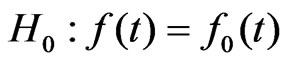on given significance level .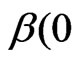

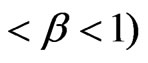Our main goal in the sequel is: to solve the problems 1) and 2). For this we have to find limit distribution of r.v.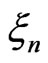. The results, obtained in this work, allow to approximate distribution of r.v. 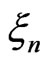with distribution of maximum of Gaussian process.

Let 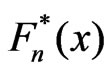be an empirical distribution function of the sample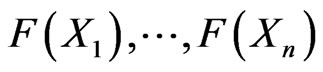, 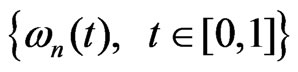be a sequence of Wiener process. Set

,

,

,.

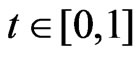
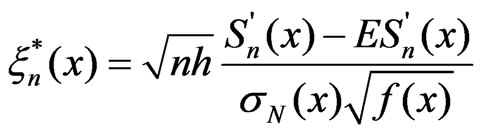
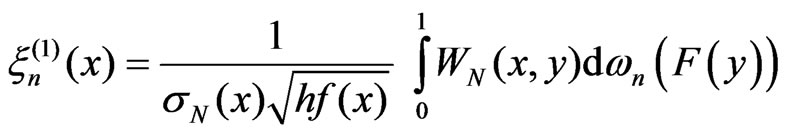
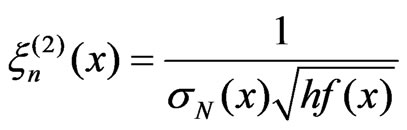
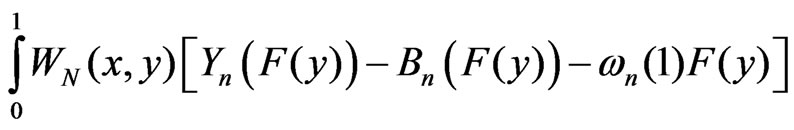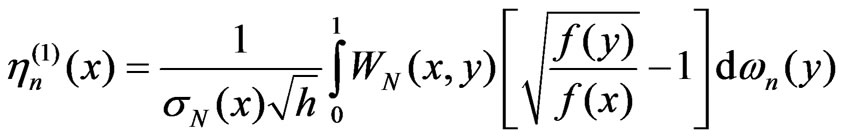
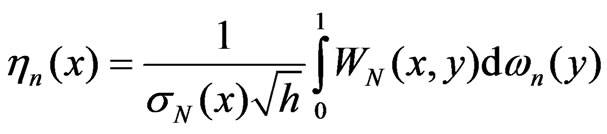It is evident that

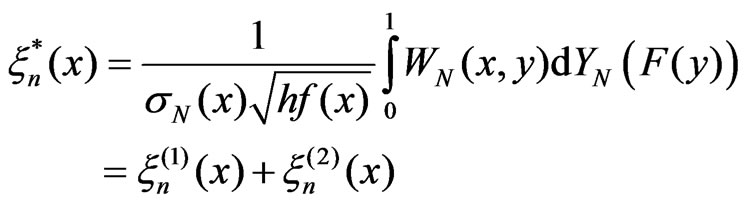
and the structure of co-variations of the Gaussian processes 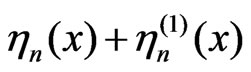and 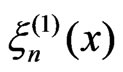is coincided.

We assume that as and the following conditions are fulfilled:

1),

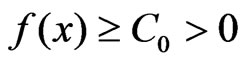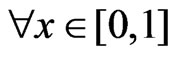
2) The pdf 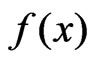continuously differentiable in the interval [0, 1].

In what follows C and c with or without index is universal positive number.

Theorem. Suppose that the conditions 1) and 2) are satisfied. Then for arbitrary 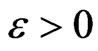one has

(1)

Also there is C such that

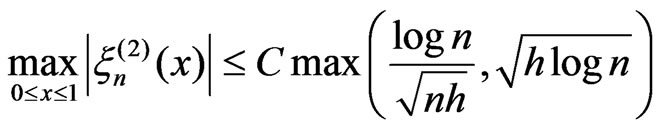(2)

with probability equal to 1. The following assertion is proved by Komlosh et al. [14].

Lemma 1. There exist a probabilistic space where it is possible to define version of the 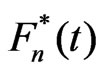and the sequence of Brownian bridge 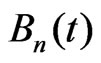such that for all x.

.

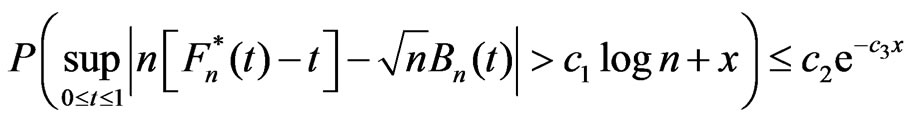Lemma 2. Let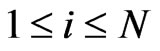. 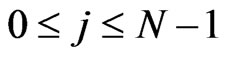For all l and J such that

where, one has

.

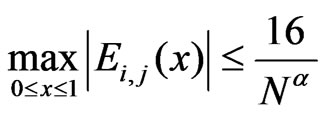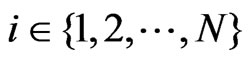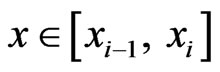Also for any and the following holds

.

the following Lemma 3 is proved in the book of Lamperty [15].

Lemma 3. Let 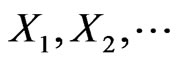be a sequence of standard normal distributed r.v.s then

3. Proofs of the Main Results

The proof of Lemma 2 is simple and hence it is omitted. The proof of the main theorem. We have

Hence

because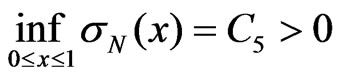. From Lemma 1 and 3 it follows that as

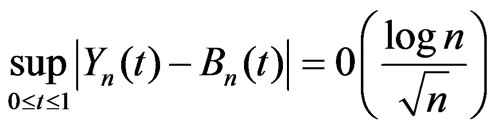and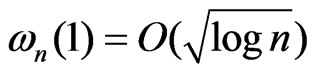

with probability equal to 1. The relation (2) follows.

Let. Then

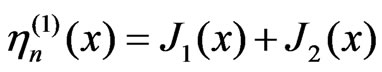
where

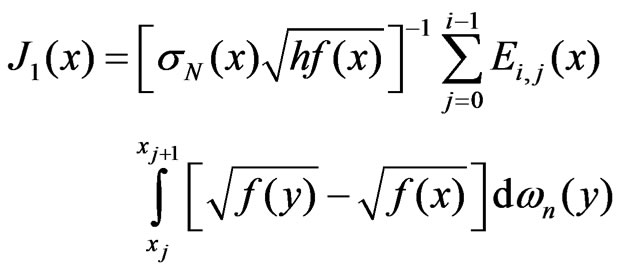
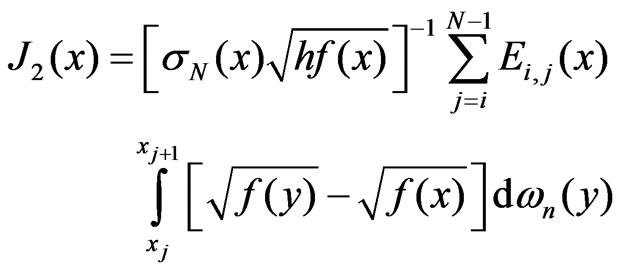
for 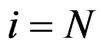we suppose. Set

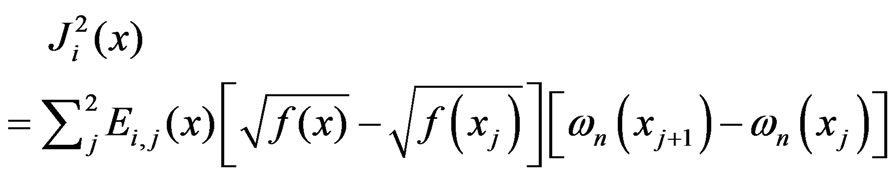
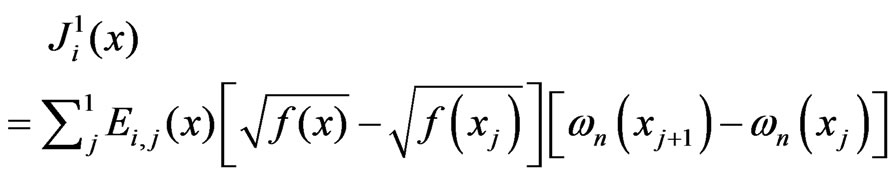
where and 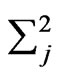are denoted a summation over all 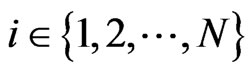and 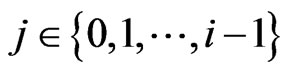satisfying the inequalities

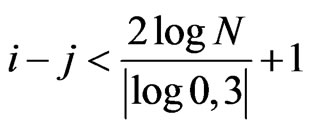(3)

and

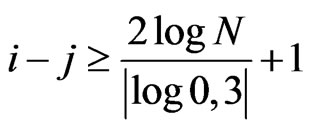(4)

respectively. Integrating by part we find

. (5)

Put

,.

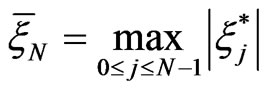Since (3)

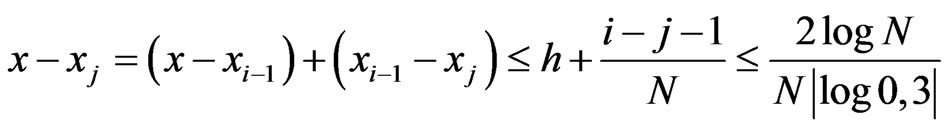
According to conditions a), b), also Lagrange’s meanvalue theorem and form the last inequality we have

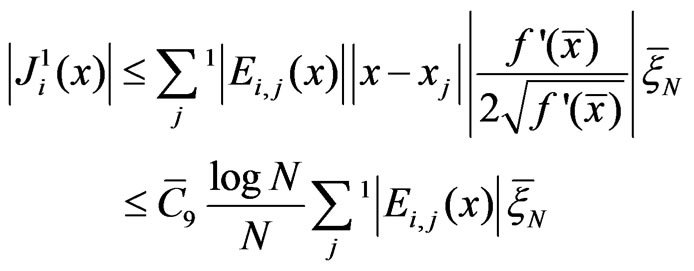
where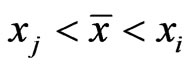. Here we take into account 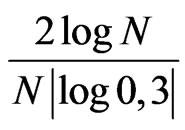too.

From lemma 2 we obtain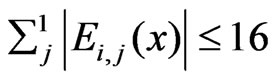. Combining above-mentioned we obtain

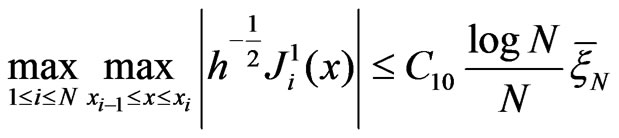. (6)

Similarly 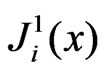we have

.

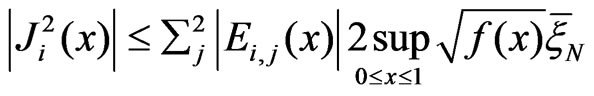By virtue of lemma 2 when (4) is fulfilled the following is true

,.

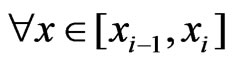As a result we have

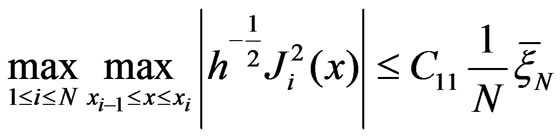(7)

Reasoning alike presented at p. 410 of Cramér [16] we find

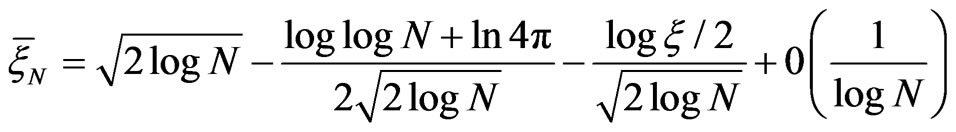(8)

where 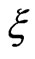is a random variable with pdf

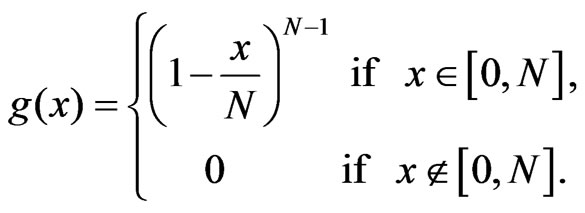
It is known (see, (29.2) of Skorohod [17]) that for arbitrary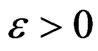

.

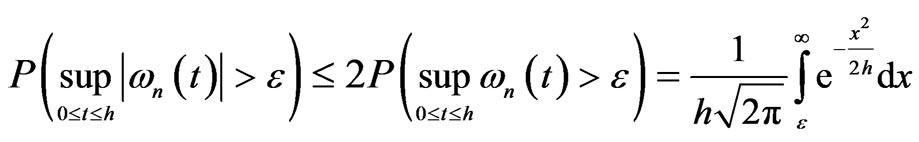Use this, (5)-(8) and Chebishev’s inequality to get

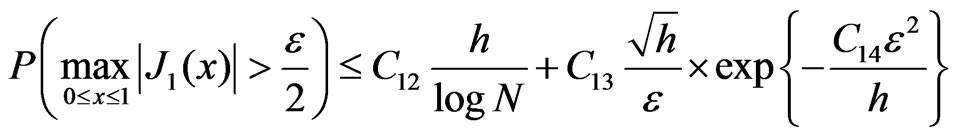(9)

By same way we can find that

(10)

The inequality (1) follows from (9) and (10). The proof of Theorem is completed.

The theorem allows to approximate the distribution of r.v. 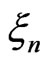by distribution of the maximum of Gaussian process.

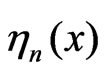4. References

[1]    N. B. Smirnov, “On Construction of a Confidence Interval for the Probability Density Function,” Soviet Reports, Vol. 74, 1959, pp. 1189-1191.

[2]    P. J. Bikel and M. Rosenblatt, “On Some Global Measures of the Deviations of Density Functions Estimates,” The Annals of Statistics, Vol. 1, No. 6, 1973, pp. 1071- 1095.

[3]    M. Rosenblatt, “On the maximal deviation of k-dimensional density estimates”, Annals of Probability, Vol. 4, No. 6, 1976, pp. 1009-1015. doi:10.1214/aop/1176995945

[4]    M. S. Muminov and Sh. A. Khashimov, “On Limit Distribution of the Maximal Deviation of Spline Density Estimators,” FAN, Tashkent, 1986.

[5]    M. S. Muminov, “On a Limit Distribution of the Maximal Level of Empirical Distribution Density and the Regression Function. I,” Theory Probability and Its Application, Vol. 55, No. 3, 2010, pp. 582-590.

[6]    M. S. Muminov, “On a Limit Distribution of the Maximal Level of Empirical Distribution Density and the Regression Function. II,” Theory Probability and Its Application, Vol. 56, No. 1, 2011, pp. 162-173.

[7]    V. D. Konakov and V. I. Piterbarg, “On the Convergence Rate of Maximal Deviations Distribution for Kernel Regression Estimates,” Journal of Multivariate Annalysis, Vol. 15, No. 3, 1984, pp. 279-294. doi:10.1016/0047-259X(84)90053-8

[8]    V. D. Konakov and V. I. Piterbarg, “High Level Excursions of Gaussian Fields and the Weakly Optimal Choice of the Smoothing Parameter. I,” Mathenatical Methods of Statistics, Vol. 4, 1995, pp. 481-434.

[9]    V. D. Konakov and V. I. Piterbarg, “High Level Excursions of Gaussian Fields and the Weakly Optimal Choice of the Smoothing Parameter. II,” Mathenatical Methods of Statistics, Vol. 1, 1997, pp. 112-124.

[10]    K. S. Lii and M. Rosenblatt, “Asymptotic Behavior of a Spline of a Density Function,” Computters & Mathematics with Applications, No. 1, 1975, pp. 223-235.

[11]    M. S. Muminov, “On Statistical Estimation of the Probability Density Function by LineFunctions,” Ph.D. Thesis, Tashkent, p. 110.

[12]    M. S. Muminov, “On Approximating the Probability of a Large Excursion a Nonstationary Gaussian Process,” Siberian Mathematical Journal, Vol. 51, No. 1, 2010, pp. 175-195. doi:10.1007/s11202-010-0015-6

[13]    K. S. Lii, “A Global Measure of a Spline Density Estimate,” The Annals of Statistics, Vol. 6, No. 5, 1978, pp. 1138-1148. doi:10.1214/aos/1176344316

[14]    Y. Komlos, P. Major and G. Tusnady, “An Approximation of Partial Sums of Independent RV’s and the Sample DF. I,” Probability Theory and Related Fields, Vol. 32, No. 1-2, 1975, pp.111-131.

[15]    G. Lamperty, “Probability,” Nauka, Moscow, 1973.

[16]    G. Cramér, “The Mathematical Method in Statistics,” Mir, Moscow, 1976.

[17]    A. V. Skorohod, “The Random Processes with Independent Increments,” Nauka, Moskov, 1964.