ABSTRACT

When writing equations of chemical dissociation, students and scholars are taught two fundamental rules to balance the equation. On both sides of the equation, the types of elements and their quantity are conserved, as well as the global electrical charge. This paper introduces additional methods during dissociation of gaseous compounds, to precisely describe how electrical charges locally move and how bonding structures are modified. Specific rules revolving around electrons pairs displacements are developed and applied to about 150 dissociations of small gaseous molecules using atoms from the three first rows of the periodic table. Results obtained tend to demonstrate the relevance of these tools for chemists.

Keywords:

Chemistry, Covalent Bonds, Even-Odd Rule, Covalent Rule, Molecule, Dissociation, Gas, Charge Position, Ion, Periodic Table

1. Introduction

In gaseous phase, chemical dissociations start with compounds in the form of molecules [1] . These compounds are then modified but the numbers of each type of atoms remain constant, as well as for the total charges of every compounds. On the contrary, atoms and charges positions are frequently displaced. Such dissociations are usually described through an equation, with compounds on the left and products on the right [2] . As the equation indicates, states before and after the dissociation, no information is given when very simple chemical steps occur. These steps may give local charges, electrons’ positions and bonds’ repartitions in every compound before, during and after each chemical step. This paper aims at giving a generic method to know the movement of electrons and thus the disappearance of covalent bonds as well as the charge borne locally by atoms. Our method relies upon the recently proposed even-odd rule [3] , and the specific periodic table for chemistry [4] . It will also be necessary to introduce a rule covering covalent bonds.

The main idea proposed in this paper is that dissociation of gaseous compounds always implies steps of a single decrease in the number of covalent bonds.

This paper will start by briefly recalling the even-odd rule, the covalent rule and the specific periodic table for gaseous molecules. Then, it will describe the three types of electron displacements that can occur in a chemical reaction, resulting in bond modifications and charges’ re-localizations. Finally, the method will be applied to numerous examples of molecular dissociations of small gaseous compounds, illustrating electrons displacements and their resulting products. In the discussion, atoms’ positions in ions or molecules from available data are compared to charged elements of a “specific periodic table for molecular dissociation”.

All along this paper:

· Atoms are represented by their acronyms as in the well-known periodic table [5] .

· In compounds drawings, a short line between atoms represents a covalent bond [6] [7] .

· To comply with the notation used in previous papers dealing with the even-odd rule, compounds are noted in capitals: CH4 is for neutral methane, CH3(+) and CH3(−) for methyl ions [3] .

· In a chemical formula, charges borne by an atom are indicated on the upper right of its acronym by a sign (positive (+) or negative (−)) [8] : sign (+) indicates one missing electron and (−) indicates one added electron.

· As dissociations imply a decrease in the number of bonds, the specific table for dissociation developed in this paper, is not directly applicable to crystals which have a higher number of bonds than in the gas phase [9] [10] .

2. Theoretical Framework

2.1. Even-Odd Rule

The even-odd rule [3] is the main theoretical foundation of ideas developed in the present article. To sum up, this rule revolves around the parity—odd or even—of the number of electrons around the nucleus. It states that:

· unbounded electrons (i.e. not involved in covalent bonds) go by pairs,

· neutral even atoms have an even number of bonds,

· neutral odd atoms have an odd number of bonds,

· charged atoms have a reversed parity of numbers of covalent bonds compared to neutral atoms,

· charged atoms do not bear more than a single positive (+) or negative (−) charge.

2.2. Covalent Bonds Rule

The second tool is the Covalent bonds rule. In this rule, covalent bonds:

· consist of a single electrons pair [4] ,

· link either two neutral atoms, a neutral atom with a charged atom or two charged atoms with opposite charges,

· cannot interconnect two atoms bearing the same charge (positive or negative),

· belong separately to each atom of the atomic pair formed by this bond.

Cases of uncharged molecules were previously investigated [6] , as well as cases of ions having a single positive or negative charge [8] . Both studies have shown that the Covalent bonds rule is appropriate for gaseous molecules. Besides, this notion of covalent bonds makes concepts like multiple charges [11] , multiple covalent bonds [12] and resonance [13] redundant. They are not used in this paper.

When the covalent bonds’ rule is used in association with the even-odd rule, it means that the total number of electrons in a compound is always even [4] .

2.3. Specific Periodic Table for Gaseous Molecules

The last used tool is a “specific periodic table for chemical dissociation” in which atoms can only form compounds in a gaseous phase with a given number of bonds. In this paper, for each element, the possible number of bonds will be derived from the recently introduced “specific periodic table for chemistry” [4] .

This specific table lists several elements and a distinction has been made between charged or uncharged elements since it changes the parity of the number of electrons.

Parts of the “specific table for gaseous molecular dissociations” are similar with the classical periodic table [5] . Other parts however indicate how charges affect the number of possible bonds.

3. Chemical Dissociations of Gaseous Compounds

To understand electrons displacement during chemical dissociation, one should usually start with balancing the reaction and comply with:

· Atoms numbers conservation i.e. mass conservation [14] .

· Overall electrical state conservation, i.e. conservation of the total number of electrons’ pairs [15] .

3.1. Compounds Representations and Atoms Conservations

This part focuses on dissociation’s reactions involving two atoms that can be part of bigger and more complex molecules. Let’s call the atoms that will be separated during the dissociation A and B, the groups of atoms that describe the rest of the molecule R1 and R2. Our molecule can hence be represented as below, with a line depicting the bond that disappears during the reaction. The other bonds in the molecule are not represented here and can be of any geometry.

A and B are two interconnected atoms with a covalent bond. As a covalent bond is composed of an electrons pair, the small line also represents an electrons pair.

Under specific physical and thermal conditions, atoms A and B can be detached from each other, and the bond’s drawing can disappear. The gaseous molecule is dissociated, resulting in two stand-alone compounds. In the following representation, the small line has vanished, and the compounds are written separately.

As the bond was an electrons pair, it is reasonable to assume that this pair has moved to another location. Reversely, this pair can come back to its previous position, hence reforming the covalent bond. The original gaseous molecule can be recomposed.

Furthermore, R1, R2, A and B are present in both drawings, in accordance with mass conservation.

3.2. Charges and Numbers of Electrons after Dissociations

The basic rule of electrons’ displacement during dissociation is that the pair of electrons forming a covalent bond is displaced as a whole: a pair of electrons never splits. Here, we study how this pair moves around.

As atoms in ions or molecules can only have three electrical states, there is a limited number of possible charges configurations when two atoms of different states are connected. Bearing in mind that two atoms with the same effective charge cannot bond, it leaves seven configurations to consider, as illustrated in the drawings below. Resulting charge states are also shown after dissociation.

The first column represents compounds before dissociations, the second is a useful pedagogical state (that has no physical existence but helps predicting on which atom the electrons pair ends) and the third column shows compounds after dissociation.

Example: In column 1 of line 2, A(+) and B(neutral) are linked. The line represents the bond, which corresponds to an electrons pair. Let’s virtually

suppose this electrons pair is entirely taken away. This would result (see column 2) in the loss of one electron for A and one for B: A(+) becomes A(++) and B(neutral) becomes B(+). If the electrons pair comes back, it would be attracted to the most positively charged atom. A(++) receiving an electron pair, becomes A(neutral). Consequently, these steps result in the production of A(neutral) and B(+) of column 3. Between column 1 and 3, the global charge state is conserved. In this reaction, it seems that (virtually) a positive charge has move from right to left.

Each dissociation listed in these drawings follows the same principle of electron pair displacements. Noticeably, the global charge state is also conserved, which remains in accordance with current theories.

3.3. Electrons Positions around the Nucleus

Let’s have a closer look at the location of electrons in atoms involved in an “association”, which corresponds to the symmetrical modeling of a dissociation.

Around its nucleus, an atom has three shells [16] . They have been named inner shell, inactive shell and covalent shell.

In the three following chapters, electrons pairs are first distributed in the two first shells and the modification of the number of electrons in covalent shells is carefully described.

3.3.1. Two Even-Atoms

In even atoms, the nucleus has an even number of protons with the same number of electrons. All these electrons are composed of unbreakable pairs distributed around the nucleus. Two neutral unbonded atoms can be drawn as:

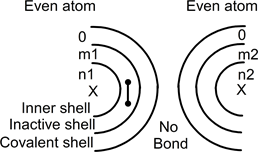
In this drawing, inner shells contain n electrons, the inactive shells m electrons: m and n are even numbers to form pairs in these shells. As the atoms are not bonded, both covalent shells are empty.

In the inactive shell of the left atom, an electrons pair is represented with a short line and two dots. Each dot is an electron. With the line in between, they form a pair. This line with its dots can move to become a covalent bond. After such a modification, both atoms may be presented as:

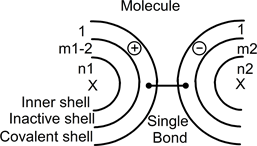
In this drawing and in the left atom, the number of electrons of the inactive shell is now m1-2: one pair has moved out to appear in both covalent shells. The short horizontal line now thus represents the new covalent bond with one point in each covalent shell. During this movement, one electron moves out from the left-side atom and is added to the right-side atom. The atom to the left is now positively charged (indicated with the (+) symbol) and the atom to the right is now negatively charged (indicated with the (−) symbol).

The total number of electrons and global charge are kept between both states. After this displacement, atoms are associated to form a single neutral molecule with two charged atoms.

3.3.2. Two Odd Elements with Opposite Charges

In the case of odd elements, the nucleus has an odd number of protons, but since the number of electrons is always even, it is translated in these elements being charged. Before the chemical association, the three shells can be drawn as:

In this drawing, n is an even number of electrons and m is an odd number of electrons. The left atom has electrons’ pairs thanks to an extra-electron and the right atom misses one also to have electrons’ pairs. The total number of electrons in each atom is even.

In the left side atom, small black line still represents a pair in the inactive shell. This electrons pair is electrically attracted by the positively charged right-side atom. The result can be drawn as (see next page):

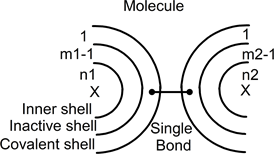
In this drawing, both atoms are now connected through a covalent bond. One electron (black dot) of the left atom has moved from the inactive shell to two covalent shells. One electron (second black dot) has moved to the covalent shell of the right-side atom. Both black dots are still attached through the small line, which represents the covalent bond between both atoms.

During this modification, the electrons pair has not been split. After that, both atoms are connected forming a single molecule with neutral atoms.

In this drawing, each covalent shell contains only one electron and the molecule has only one covalent bond.

3.3.3. Two Atoms with Different Parity

In the case of an odd atom and an even atom, one nucleus has an odd number of protons with an even number of electrons around it. Furthermore, the other has an even number in and around the nucleus. The parity of the system imposes a single positively or negatively charged of the odd atom. Taking the case of a negative charge, both atoms can be drawn as:

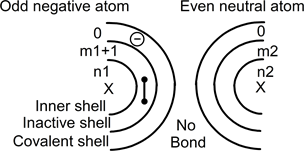
In this drawing, the left side odd atom has one added electron: even numbers (m1+1) and n1 of electrons around the nucleus. With this configuration, an electrons pair can move to form a covalent bond between both atoms as follow:

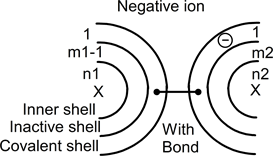
The pair moves from the left inactive shell into both covalent shells. One electron still belongs to the left atom and the second has moved to belong to the right atom. This pair has moved in order to associate two atoms and to form a single ion. The extra electron, i.e. the negative charge, seems (virtually) to have moved from left to right.

4. Bonds Numbers and Covalent Bond Displacements

It can be said from all drawings of chapter 3 that:

· In chemical association, a pair always comes from a shell below the covalent shell.

· In chemical dissociation the reverse must be considered.

5. Application to Small Gaseous Compounds

Compounds used in this chapter are composed of atoms from the three first rows of the classical periodic table [5] . However, these atoms are now classified in a “specific periodic table for dissociation” of gaseous molecules in which electrons charges are included. The result is shown in Table 1.

In Table 1, inorganic elements are in white cells and organic elements are in green cells. Between white and green cells, yellow colored cells show semi-organic elements.

In the three rows of Table 1, neutral elements are placed in the middle of each cell. These neutral elements can be components of all the well-known gaseous compounds (H2O, NH3, BF3 etc.).

Charges of the elements are placed laterally below the names. Signs (+) or (−) are just near the element’s name. For example: Al(+) can be either AlF2(+) with two bonds or mono-atomic Al(+) without bond.

Table 1 indicates how many bonds an element may have depending on its electrical states. Interestingly, fluorine in its neutral state can only have one bond when in a gaseous compound like HF, and no bond at all after its dissociation.

Table 1 and the above-mentioned rules must be used in the following to illustrate electrons displacement in the dissociation of several small gaseous ions or molecules. Corresponding small gaseous molecules are listed in Table 2.

Bonds and molecule’s names (columns 1 and 2 of Table 2) are extracted from the US National Bureau of Standards book [17] , a widely recognized reference on dissociation reactions. However, this comprehensive list of products and their dissociations, derived from published experiments, lacks key information: charges locations after the bond have been severed and remain mostly unknown. Charges positions drawn in columns 3 and 4 of Table 2 remediate to this shortcoming by detailing where electrons pairs from the covalent bond end.

On each line of Table 2, the overall electrical charge is kept between columns 3 and 4, i.e. before and after dissociations.

As a result, Table 2 confirms the main idea proposed in this paper. For the record, it asserts that dissociations always imply a step of a single decrease in the number of covalent bonds i.e. displacement of an electrons’ pair.

These observations strongly support theories that have been argued in previous papers [3] [4] [6] [8] [11] .

6. Discussions

Table 1 can now be compared with available chemical dissociations written in Table 2. These require to focus our attention on the number of bonds in each cell of Table 1.

6.1. Neutral Elements in Stable Compounds

In Table 1, known neutral gaseous compounds have the highest number of bonds. In row 2, it starts at one bond for Lithium (LiF) up to 4 bonds for carbon (CH4). It then, decreases from 3 for nitrogen (NH3) down to 1 for fluorine [18] . In Table 2, these seven neutral elements in well-known gases, also exhibit these numbers of bonds. Other examples include neutral LiF, BeF2, BF3, CH4, NH3, H2O and HF, appearing in both tables. Since one can make the same observation for the other stable gases, it seems therefore that, for stable gases, rules and experiments strongly support each other.

6.2. Mono-Atomic Compounds

Table 1 also indicates the lowest number of bonds an element can have and become mono-atomic after dissociation. Observations are summed up below:

· Only uncharged even atoms and charged odd atoms can be mono-atomic i.e. without bond. In row 2 of Table 1, these neutral-even mono-elements are Be, C, O, whereas charged-odd mono-elements are Li(+), Li(−), B(+), B(−), N(+), N(−), F(+), F(−). All these mono-atomic elements exist in Table 2. Once again, all these elements point toward the accuracy of the theory behind this paper.

· uncharged odd atoms cannot be in a mono-atomic form. They only pair with other elements through one covalent bond: H2, LiF, BF, NH, HF.

All these formulas are in both Tables.

Every mono-elements have electrons pairs in their inactive shells. They are very reactive. Consequently, they can rapidly restructure the gaseous molecules they come from.

The author has compared mono-atomic elements of Table 1 with the available list of oxidation states [19] without finding a complete agreement.

6.3. Semi-Organic Elements

In row 2 of Table 1, a semi-organic element is present only in column 4. It is neutral carbon with 4, 2 or 0 bonds. In the same cell, C(+) is inorganic and C(−) is organic. Corresponding small compounds can be CH4(neutral), CH3(+), CH3(−) and CH2 [20] . When with a lower number of bonds, these compounds become reactive compounds as mentioned in Table 2.

This also confers weight to the ideas developed in this paper.

6.4. Electrons Pairs in Chemical Dissociations

This paper considers that electrons pairs cannot be split. During dissociation, a pair moves out from a connection to slip into one of the atoms. Different cases occur:

· In white cells of Table 1, the number of electrons in the inner shell is constant. When a dissociation occurs, the covalent pair moves into the inactive shell, transforming this atom to become very reactive.

· In green cells of Table 1. The number of electrons in the inner shell is not constant. When a dissociation occurs, one pair goes either in the inactive shell or in the inner shell: H2O gives HO(−) with a pair added in the inner shell or HO(+) with a pair going out of the inner shell into the inactive shell. When in these configurations, compounds are very reactive.

Consequently, for compounds dissociations, the number of electrons’ pairs remains the same.

6.5. Dissociation of Small Gaseous Compounds

Dissociations in a known volume of a gas were carefully studied with a known volume of gas [17] . These experiments showed that when subjected to the right conditions for dissociation, only a small quantity of dissociated molecules is present, compared to the rest of the initial gas molecules. According to the present paper, this is surely due to a high reactivity of the dissociated molecules, that keep recombining to for the initial gas. The proposed reason for this reactivity is the number of electrons in the inactive shell, as shown in Table 1: the more electrons in the inactive for inorganic element and in the inner shell for organic elements, the more reactive the atom is.

As dissociated compounds are now known without ambiguity to be conform to both Tables, this knowledge is a very significant base for this paper.

7. Conclusion

In this paper, known chemical dissociations of gaseous small molecules were considered in the light of recent theoretical ideas, based upon rules named even-odd and covalent rules. The novelty is the presence of single charged atoms in chemical compounds. A “specific periodic table for dissociation of gaseous molecules” is proposed including atoms’ charges of each element. This specific table allows displacement of electrons’ pairs and a formulation of a basic chemical step for dissociation of small compounds. About 150 dissociations of small gaseous molecules using atoms from the three first rows of the periodic table were studied and found to be compatible with the exposed theory. This constitutes a very significant support for the ideas proposed in this paper and relevance of these tools for chemists.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

Cite this paper

Auvert, G. (2019) Basic Steps in Chemical Dissociation of Gaseous Molecules Using an Even-Odd Rule, a Specifically Adapted Periodic Table and a Covalent Bonding Rule. Open Journal of Physical Chemistry, 9, 88-105. https://doi.org/10.4236/ojpc.2019.92006

References