Open Journal of Microphysics
Vol.3 No.2(2013), Article ID:31738,4 pages DOI:10.4236/ojm.2013.32008
Darboux Transformation in Quantum Black-Scholes Hamiltonian and Supersymmetry
1Department of Physics, Islamic Azad University—Ayatollah Amoli Branch, Amol, Iran
2Department of Statistics, Mazandaran University, Babolsar, Iran
3Department of Physics, Imam Hossein University, Tehran, Iran
Email: pouriya@ipm.ir
Copyright © 2013 Jafar Sadeghi et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received January 22, 2013; revised February 24, 2013; accepted March 5, 2013
Keywords: Black-Scholes Hamiltonian; Darboux Transformation; Supersymmetry
ABSTRACT
In this paper, we consider the Black-Scholes (BS) equation for option pricing with constant volatility. Here, we construct the first-order Darboux transformation and the real valued condition of transformed potential for BS corresponding equation. In that case we also obtain the transformed of potential and wave function. Finally, we discuss the factorization method and investigate the supersymmetry aspect of such corresponding equation. Also we show that the first order equation is satisfied by commutative algebra.
1. Introduction
As we know, there are several methods to study for the integrability model. One of the method, we focus here, is Darboux transformation. It is well known that the Darboux transformation [1] is one of the major tools for the analysis of physical systems and for finding new solvable systems. Using a linear differential operator, Darboux construct solutions of one ordinary differential equation in terms of another ordinary differential equation. It has been shown that the transformation method is useful in finding soliton solutions of the integrable systems [2-4] and constructing supersymmetric quantum mechanical systems [5-7]. Also, more general solvable cases were obtained by means of factorization methods [8] and via lie algebraic approaches [9-13]. Darboux transformation is known as one of the most powerful methods for finding solvable Schrodinger equations with constant mass, in the context of which it is also called supersymmetric factorization method [14]. On the other hand, during the past few years there has been great interest in studying problems of fiance using various tools of physics [15]. In that case also quantum mechanics has been used to analyze option pricing, stock market returns [16,17] and the Black-Scholes (BS) equation [18-21]. The BS equation plays an important role in option pricing. The solution of such equation may be found by mapping it into a Schrodinger-like equation. So, we take advantage from Darboux transformation to this equation and obtain the generalized form of BS equation.
The Darboux transformation has been extensively used in quantum mechanics in the search of isospectral potential for exactly Schrodinger equations of constant mass and position-dependent mass [22-27]. So, we take advantage from such transformation and obtain the effecttive potential, modified wave function and shape invariance condition and generators of supersymmetry algebra. For the BS Hamiltonian help us to transform of the corresponding potential.
This paper is organized as follows. We first introduce Quantum BS Hamiltonian and apply the Darboux transformation to such equation. In that case we show that the corresponding Hamiltonian changes to new form of potential. Finally, we study the supersymmetry version and shape invariance condition for transformed BS Hamiltonian.
2. Darboux Transformation and BS Hamiltonian
As we know the BS equation for option pricing with constant volatility is given by,
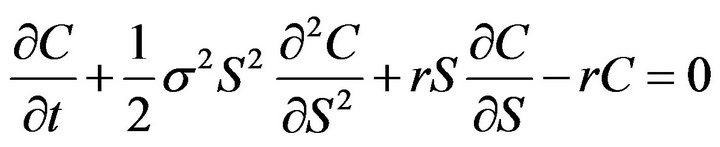 (1)
(1)
where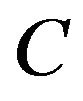 ,
,  ,
,  and
and  denote the price of the option, the stock price, the volatility of the stock price and the risk-free spot interest rate respectively. Now we consider the following generalized BS equation in (1 + 1)-dimension by using the Darboux transformation operator technique [26,27],
denote the price of the option, the stock price, the volatility of the stock price and the risk-free spot interest rate respectively. Now we consider the following generalized BS equation in (1 + 1)-dimension by using the Darboux transformation operator technique [26,27],
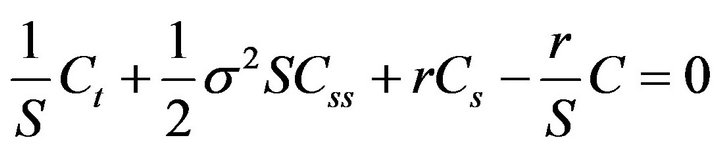 (2)
(2)
Now, we take ,
, 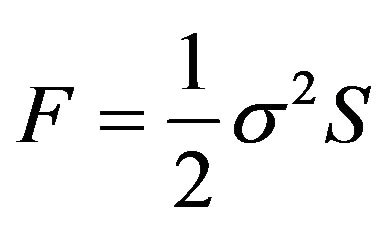 ,
, 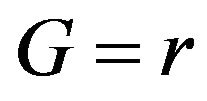 and the potential
and the potential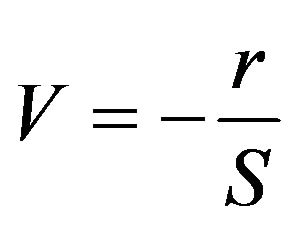 . Here we can rewrite the above equation as,
. Here we can rewrite the above equation as,
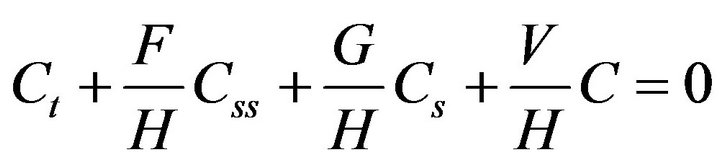 (3)
(3)
and
 (4)
(4)
In order to have same Equation as (2) with different of potential,
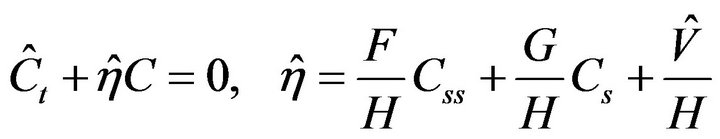 (5)
(5)
Here, we have , this lead us to imply
, this lead us to imply . In order to obtain the modified potential
. In order to obtain the modified potential 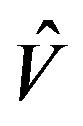 and corresponding wave function for Equation (5), we introduce operator
and corresponding wave function for Equation (5), we introduce operator  which are called Darboux transformation. The general form of such translation Durboux transformation will be as
which are called Darboux transformation. The general form of such translation Durboux transformation will be as
 (6)
(6)
and we take special case as . Also we note here there are some following properties for this Darboux transformation,
. Also we note here there are some following properties for this Darboux transformation,
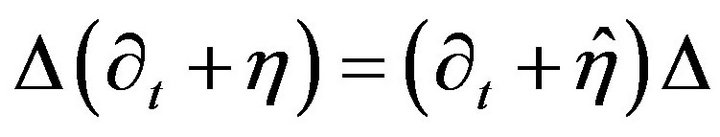 (7)
(7)
and
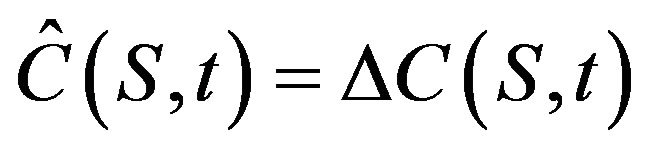 (8)
(8)
In order to obtain the parameter  we need to use the Equations (2) and (7), so we have,
we need to use the Equations (2) and (7), so we have,
 (9)
(9)
Making linear independence of 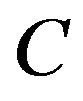 and its partial derivatives, we collect their respective coefficients and equal them to zero, from which we can obtain the following system about the functions
and its partial derivatives, we collect their respective coefficients and equal them to zero, from which we can obtain the following system about the functions  and
and ,
,
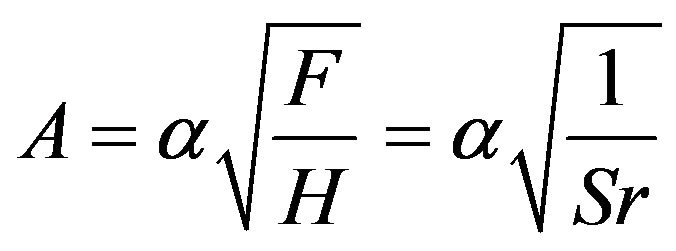 (10)
(10)
as we know the usual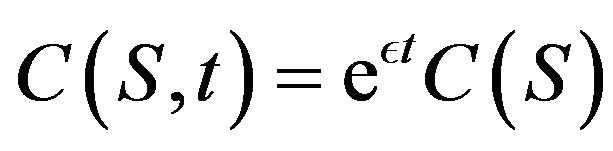 , so the
, so the  will be as,
will be as,
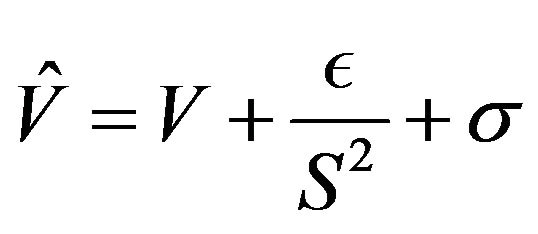 (11)
(11)
which is modified potential and obtained by the Darboux transformation. By using the Equation (8) one can calculated the corresponding wave function 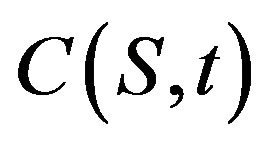 as,
as,
 (12)
(12)
3. Supersymmetry and Darboux Transformation
In what follows we will prove that the formalism of supersymmetry for our generalized BS equation is equivalent to the Darboux transformation. Here we suppose the BS operator 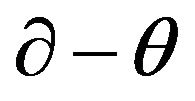 is self adjoint,
is self adjoint,
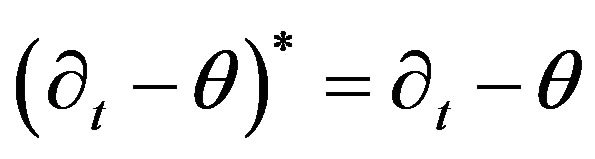 (13)
(13)
Taking the operation of conjugation on Darboux transformation (7), we obtain
 (14)
(14)
where the operator  adjoint to
adjoint to  is given by,
is given by,
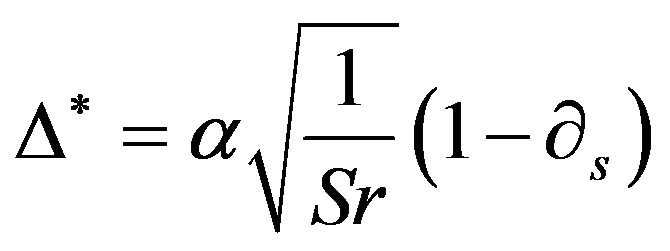 (15)
(15)
Equations (4) and (5) can then be rewritten as one single matrix equation of the form,
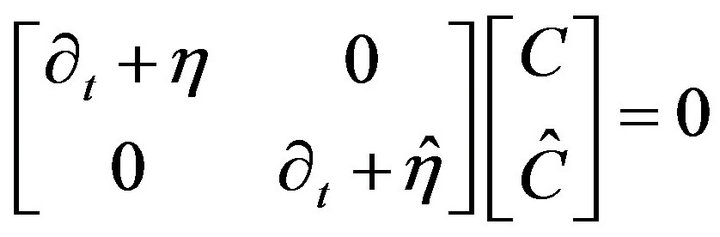 (16)
(16)
Assuming that 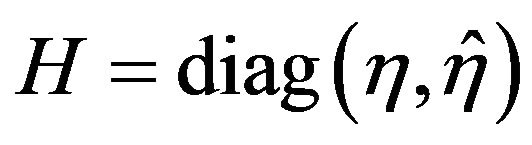 and
and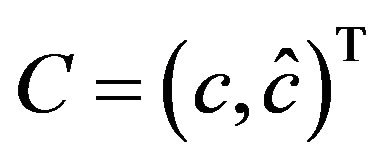 , the above equation can be written as,
, the above equation can be written as,
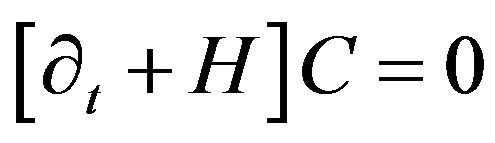 (17)
(17)
Two supercharge operators 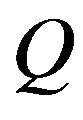 and
and  are defined as follows,
are defined as follows,
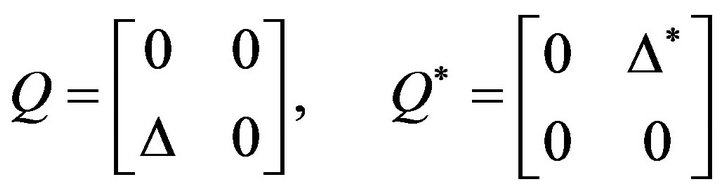 (18)
(18)
where  and
and  are the operator given by Equations (6) and (15), respectively. One can show that the Hamiltonian H satisfies the following expressions,
are the operator given by Equations (6) and (15), respectively. One can show that the Hamiltonian H satisfies the following expressions,
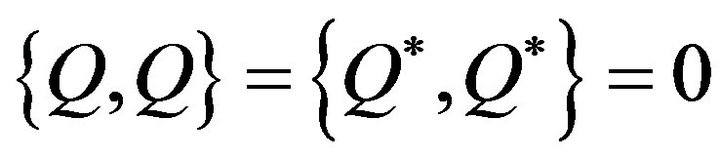

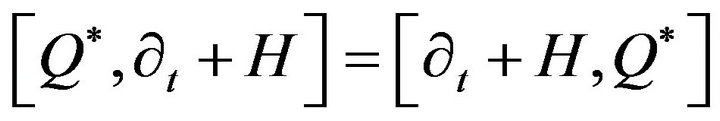 (19)
(19)
Considering the complementing relations of the supersymmetry algebra; the anti commutators 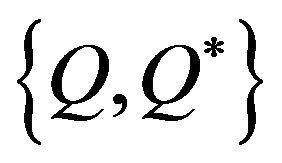
and , we obtain the operators
, we obtain the operators 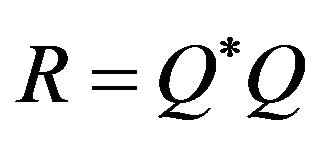 and
and
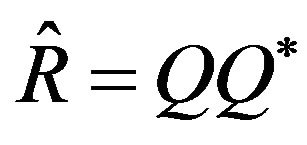 and consider the relations of them with our Hamiltonian
and consider the relations of them with our Hamiltonian 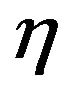 and
and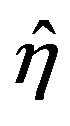 . So, one obtain the
. So, one obtain the 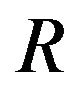 and
and  as follow,
as follow,
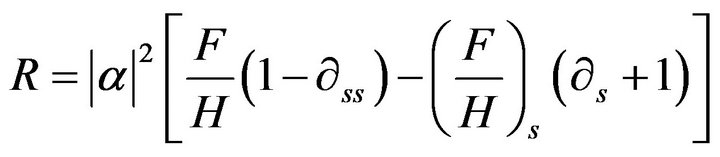 (20)
(20)
and
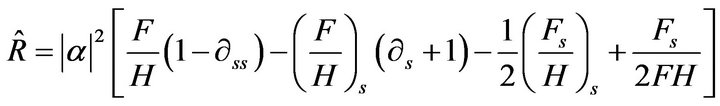 (21)
(21)
where the indices 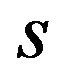 will be derivative with respect to
will be derivative with respect to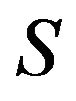 . In order to have shape invariance and supersymmetric algebra we need to obtain the
. In order to have shape invariance and supersymmetric algebra we need to obtain the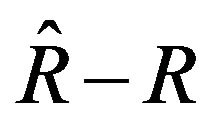 . If such value be constant and zero there is some supersymmetry partner for the such system. Otherwise we need to apply some condition in
. If such value be constant and zero there is some supersymmetry partner for the such system. Otherwise we need to apply some condition in 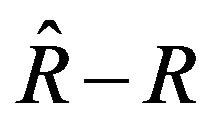 to have constant value. So, one can obtain the following equation for the
to have constant value. So, one can obtain the following equation for the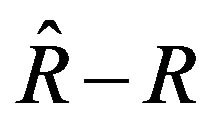 ,
,
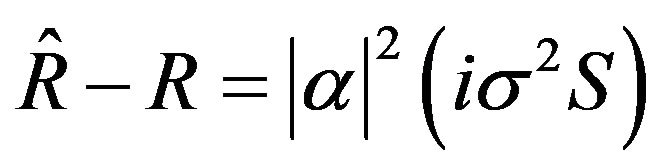 (22)
(22)
We mention here that if we want to supersymmetry algebra we need to have also the following commutation relation, and also anti-commutation relation between  and
and ,
,
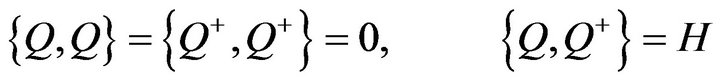 (23)
(23)
Finally we can say that the Equations (18), (19) and (23) lead us to apply the condition on the Equation (22) such that the expression 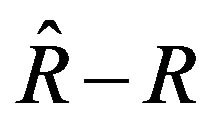 be constant. So, in that case,
be constant. So, in that case,  must be function of
must be function of 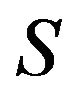 such as
such as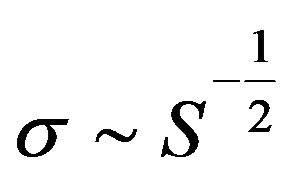 .
.
4. Conclusion
In this paper we studied the Black-Scholes (BS) equation. We used the first-order Darboux transformation and applied to the BS equation. In order to relate between supersymmetry and Darboux transformation we discussed the supersymmetry algebra and its commutation and anti-commutation super algebra. We have shown that for the satisfying such anticommutation supercharges the 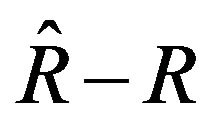 must be constant. Also, we applied the condition on the
must be constant. Also, we applied the condition on the 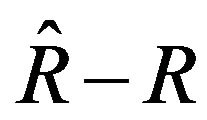 and shown that
and shown that  will be function of S as
will be function of S as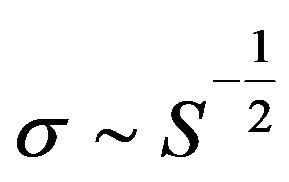 . This condition completely guarantees relation between supersymmetry and Darboux transformation.
. This condition completely guarantees relation between supersymmetry and Darboux transformation.
REFERENCES
- G. Darboux, “Sur une Proposition Relative aux Équations Linéaires,” Comptes Rendus, Vol. 94, 1882, pp. 1456-1459.
- V. B. Matveev and M. A. Salle, “Darboux Transformations and Solitons,” Springer, Berlin, 1991. doi:10.1007/978-3-662-00922-2
- M. J. Ablowitz and H. Segur, “Solitons and the Inverse Scattering Transform,” SIAM, Philadelphia, 1981. doi:10.1137/1.9781611970883
- C. H. Gu, H. S. Hu and Z. X. Zhou, “Darboux Transformations in Integraable Systems,” Springer, Dordrecht, 2005.
- E. Witten, “Constraints on Supersymmetry Breaking,” Nuclear Physics B, Vol. 202, No. 2, 1982, pp. 253-316. doi:10.1016/0550-3213(82)90071-2
- Q. P. Liu and X. B. Hu, “Bilinerarization of N = 1 Supersymmetric Korteweg-de Vries Equation Revisited,” Journal of Physics A: Mathematical and General, Vol. 38, No. 28, 2005, pp. 6371-6378. doi:10.1088/0305-4470/38/28/009
- F. Cooper, A. Khare and U. Sukhatme, “Supersymmetry and Quntum Mechanics,” Physics Reports, Vol. 251, No. 5-6, 1995, pp. 267-285. doi:10.1016/0370-1573(94)00080-M
- A. R. Piastino, et al., “Supersymmetry Approach to Quantum Systems with Position-Dependent Effective Mass,” Physical Review A, Vol. 60, No. 6, 1999, pp. 4318-4325. doi:10.1103/PhysRevA.60.4318
- R. Kok and M. Koka, “A Systematic Study on the Exact Solution of the Position Dependent Mass Schrödinger Equation,” Journal of Physics A: Mathematical and General, Vol. 36, No. 29, 2003, p. 8105. doi:10.1088/0305-4470/36/29/315
- J. Sadeghi, “Superalgebras for Three Interacting Particles in an External Magnetic Field,” The European Physical Journal B, Vol. 50, No. 3, 2006, pp. 453-457. doi:10.1140/epjb/e2006-00150-9
- H. Fakhri and J. Sadeghi, “Supersymetry Approaches to The Bound States of the Generalized Wood-Saxon Potential,” Modern Physics Letters A, Vol. 19, No. 8, 2004, p. 615. doi:10.1142/S0217732304013313
- J. Sadeghi and M. Rostami, “The Supersymmetry Approaches to the Non-Central Kratzer Plus Ring-Shaped Potential,” International Journal of Theoretical Physics, Vol. 48, No. 10, 2009, pp. 2961-2970.
- J. Sadeghi, “Dirac Oscillator with Minimal Lengths and Free Particle on AdS2 and S2,” Journal of Mathematical Physics, Vol. 48, No. 11, 2007, Article ID: 113508. doi:10.1063/1.2804773
- B. G. Idis, M. M. Musakhanov and M. Sh. Usmanov, “Application of Supersymmetry and Factorization Methods to Solution of Dirac and Schrödinger Equations,” Theoretical and Mathematical Physics, Vol. 101, No. 1, 1984, pp. 1191-1199.
- R. M. Mantega and E. Stanley, “Introduction to Econophysics,” Cambridge University Press, Cambridge, 1999. doi:10.1017/CBO9780511755767
- V. Linetsky, “The Path Integral Approach to Financial Modeling and Options Pricing,” Computational Economics, Vol. 11, No. 1-2, 1998, pp. 129-163.
- M. Contreras, et al., “A Quantum Model of Option Pricing: When Black-Scholes Meets Schrödinger and Its SemiClassical Limit,” Physica A: Statistical Mechanics and its Applications, Vol. 39, No. 23, 2010, pp. 5447-5459. doi:10.1016/j.physa.2010.08.018
- E. E. Haven, “A Discussion on Embedding the BlackScholes Option Pricing Model in a Quantum Physics Setting,” Physica A: Statistical Mechanics and its Applications, Vol. 304, No. 3-4, 2002, pp. 507-524.
- E. E. Haven, “A Black-Scholes Schrödinger Option Price: ‘Bit’ versus ‘Qubit’,” Physica A: Statistical Mechanics and Its Applications, Vol. 324, No. 1-2, 2003, pp. 201- 206.
- E. E. Haven, “The Wave-Equivalent of the Black-Scholes Option Price: An Interpretation,” Physica A: Statistical Mechanics and its Applications, Vol. 344, No. 1-2, 2004, pp. 142- 145. doi:10.1016/j.physa.2004.06.105
- O. A. Choustova, “Quantum Bohmian Model for Financial Markets,” Physica A: Statistical Mechanics and its Applications, Vol. 374, No. 1, 2007, pp. 304-314. doi:10.1016/j.physa.2006.07.029
- J. Morales, J. J. Pena and J. L. Lopez-Bonilla, “Generalization of the Darboux Transform,” Journal of Mathematical Physics, Vol. 42, No. 2, 2001, p. 966. doi:10.1063/1.1334904
- J. J. Pena, G. Ovando, D. Morales-Guzman and J. Morales, “Solvable Quartic Potentials and Their Isospectral Partners,” International Journal of Quantum Chemistry, Vol. 85, No. 4-5, 2001, pp. 244-250. doi:10.1002/qua.10042
- J. Morales, J. J. Pena and A. Rubio-Ponce, “New Isospectral Generalized Potentials,” Theoretical Chemistry Accounts, Vol. 110, No. 6, 2003, pp. 403-409. doi:10.1007/s00214-003-0494-7
- A. Rubio-Ponce, J. J. Pena and J. Morales, “One-Parameter Isospectral Solutions for the Fokker-Planck Equation,” Physica A: Statistical Mechanics and its Applications, Vol. 339, No. 3-4, 2004, pp. 285-295. doi:10.1016/j.physa.2004.03.022
- A. Schulze-Halberg, “Effective Mass Hamiltonians with Linear Terms in the Momentum: Darboux Transformations and Form-Preserving Transformations,” International Journal of Modern Physics A, Vol. 22, No. 8-9, 2007, p. 1735. doi:10.1142/S0217751X07035021
- A. Schulze-Halberg, “Darboux Transformations for Effective Mass Schrodinger Equations with Energy-Dependent Potentials,” International Journal of Modern Physics A, Vol. 23, No. 3-4, 2008, p. 537. doi:10.1142/S0217751X0803807X

