Open Journal of Geology
Vol.04 No.10(2014), Article ID:51001,17 pages
10.4236/ojg.2014.410039
Gravity Model for an Anomalous Body Located in the NW Portion of the Douala Sedimentary Sub-Basin, Cameroon (Central Africa)
Eric N. Ndikum1,2*, Charles T. Tabod1,3, Bernard Z. Essimbi1, Fidèle Koumetio4, Noutchogwe C. Tatchum5
1Department of Physics, University of Yaoundé 1, Yaoundé, Cameroon
2Department of Fundamental Sciences, Higher Technical Teacher Training College (HTTTC) Bambili, The University of Bamenda, Bamenda, Cameroon
3Department of Physics, Faculty of Science, The University of Bamenda, Bamenda, Cameroon
4Department of Physics, Faculty of Science, University of Dschang, Dschang, Cameroon
5Department of Physics, Higher Teacher Training College (HTTC) Bambili, The University of Bamenda, Bamenda, Cameroon
Email: *ndikumeric@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 August 2014; revised 24 September 2014; accepted 18 October 2014
ABSTRACT
Gravity studies have been carried out in the Douala sub-basin which is a sedimentary basin located both onshore and offshore on the South coast of Cameroon between latitudes 3˚03'N and 4˚06'N and longitudes 9˚00' and 10˚00'E, covering a total surface area of 12,805 km2. On its onshore portion, the Douala sub-basin has a trapezoic shape and covers a total surface area of about 6955 km2 while the offshore part covers an area of about 5850 km2. Gravity data used in this study are constituted of 912 gravity data points located between longitudes 8˚10.2' to 10˚59.4'E and latitudes 2˚30.6' to 4˚59.4'N and the study area is located to the NW section of the onshore portion of the Douala sub-basin. This study area is characterised by considerably high positive anomalies attaining peak values of about 104.1 mGals at longitude 9˚9.9' and latitude 4˚1.1' with contour lines which are mostly oriented in the NNE direction. Residual anomalies were extracted by upward continuation of the Bouguer anomaly field at an optimum height of 30 km. This residual field and those obtained by the separation of polynomial of order 4 had a very high correlation coefficient factor of 0.979. The multi-scale horizontal derivative of the vertical derivative (MSHDVD) method was applied on the extracted residual anomalies for the delimitation of possible contacts in the source while the amplitude spectrum was used to estimate the depth to the top of the potential field source. The MSHDVD method did not delimite any clear cut contacts in the source but the amplitude spectrum estimated the potential field source at a depth of about 4.8 km. The ideal body theory was used to determine the density contrast along a 65 km NW-SE profile yielding a value of 0.266 g/cm3. 2.5D modelling aimed at bringing out the underlying structural layout of this study area presents a source body which is very probably an intrusive igneous block surrounded by sedimentary formations and having a density of 2.77 g/cm3 at a depth of about 5.88 km below the surface and an average thickness of about 26.95 km.
Keywords:
Douala Sub-Basin, Sedimentary Basin, Bouguer Anomaly, Residual Field, Upward Continuation, 2.5D Model, Intrusive Igneous Block

1. Introduction
Two major basins make up the Cameroon Atlantic basin localized in the Gulf of Guinea which is one of the West African coastal basins, they are: the Douala/Kribi-Campo basin and the Rio Del Rey basin [1] . The Douala/ Kribi-Campo and the Rio Del Rey basins alongside the Gabon, Congo, Kwanza (also spelled Cuanza after two Angola provinces and the Cuanza River), Benguela and Namibe Basins, all share common structural and stratigraphic characteristics and so are grouped together as the West-Central Coastal Province; all these basins form the Aptian salt basin of equatorial west Africa (Figure 1) [2] . The Douala/Kribi-Campo and the Rio Del Rey sedimentary basins are separated in their onshore portion by the volcanic massif of Mount Cameroon but both form only one sedimentary unit offshore. The Douala/Kribi-Campo basin is constituted of two sub-basins: the Douala sub-basin to the North and the Kribi-Campo sub-basin to the South (Figure 2).
Figure 1. Location map for the West-Central Coastal Province, showing the approximate locations of the Douala/Kribi- Campo, Rio Muni, Gabon, Congo, Kwanza (Cuanza), Benguela, and Namibe Basins with their associated fracture zones, structural arches and highs, and volcanic axes in the Aptian salt basin of equatorial west Africa. In the index map, the West-Central Coastal Province is outlined in red. Abbreviation: Eq. Guinea, Equatorial Guinea [2] .
Figure 2. Location map of Cameroon (West Africa) and outlines of the Douala and Kribi/Campo sedimentary sub-basins. (Modified from SNH (1999) in: [7] ).
The Douala sub-basin is located between the Cameroon Volcanic Line (CVL) [3] -[5] in the north and the Kribi-Campo sub-basin in the south. It is characterized by a low surface of erosion (<200 m altitude) which corresponds to interfluves with convex and convexo-concave hillsides joined to narrow and more or less deep valleys [6] .
The gradual North-South opening of the South Atlantic is linked to the formation of the Douala sub-basin, which resulted in the diachronism of deposits from South to North and a temporal and spatial variation of sedimentary environments along the West African coast [1] .
It is worth noting that the structural dynamics that led to the formation of the sedimentary basin of Douala/ Kribi-Campo like other basins of the West African coast has resulted in the sequence variability of deposits by sector considered. Moreover, many of the works carried out in this sub-basin are unpublished because of the known confidentiality characterizing the oil research domain [7] .
In this study, gravity data has been processed for 2.5D models to bring out the underlying structural layout of the NW onshore portion of the Douala sub-basin characterized by strong positive Bouguer anomalies (Figure 3 and Figure 7).
Figure 3. Bouguer anomaly map with study area indicated by black rectangle.
2. Geological and Tectonic Setting
2.1. Geological Setting
The Douala sub-basin is a sedimentary basin which lies both onshore and offshore on the South coast of Cameroon between latitudes 3˚03'N and 4˚06'N and longitudes 9˚00'E and 10˚00'E, covering a total surface area of 12,805 km2 (Figure 2). This basin has a crescent shape which starts from the south-eastern border of Mount Cameroon with the onshore part of about 70 km wide (in the N20E direction) and extends throughout the atlantic coast showing a gradual decrease in width of the onshore part towards the South up to Londji (located to the North of Kribi). It is has the Cameroon volcanic line as its northern limit, the Kribi-Campo sub-basin as the southern limit (which is more difficult to define), and the late Proterozoic Pan-African belt as its eastern limit. The onshore part of the Douala sub-basin has a trapezoic shape and covers a total surface area of about 6955 km2 while the offshore part covers a surface area of about 5850 km2 [7] .
The Douala sub-basin has a basic stratigraphy which is interpreted to comprise of pre-rift, rift, transition and drift megasequences related to the tectonic evolution over African cratonic basement and associated Atlantic margin. The regional stratigraphy and tectonics can be summarized in four main phases of evolution related to pre, syn and post-rift separation of Africa from South America [1] .
The Douala sub-basin has a lithostratigraphy which consists of seven major Formations related to its geodynamic and sedimentary evolution [8] -[10] . They include: 1) The syn-rift period represented by the Mundeck Formation (Aptian-Cenomanian) which is discordant onto the Precambrian basement and consists of continental and fluvio-deltaic deposits, i.e., clays, coarse-grained sandstones, conglomerates. The postrift sequence includes: 2) the Logbadjeck Formation (Cenomanian-Campanian), discordant onto the Mundeck Formation and composed of microconglomerates, sand, sandstone, limestone, and clay; 3) the Logbaba Formation (Maastrichtian), mainly composed of sandstone, sand and fossiliferous clay; 4) the N’kapa Formation (Paleocene-Eocene), rich in marl and clay with lenses of sand and fine to coarse-grained crumbly sandstone; 5) the Souellaba Formation (Oligocene) lying unconformably on N’kapa deposits and characterized by marl deposits with some interstratified lenses and sand channels; 6) the Matanda Formation (Miocene), dominated by deltaic facies interstratified with volcano-clasties layers; and 7) the Wouri Formation (Plio-Pleistocene) which consists of gravelly and sandy deposits with a clayey or kaolinic matrix [6] .
Syn-rift rocks are known to exist in the Rio Muni, Douala, and Kribi-Campo Basins of Equatorial Guinea and Cameroon (Figure 1) [2] .
The oldest post-rift rocks in the Douala sub-basin (as well as in the Kribi-Campo, and Rio Muni Basins), are represented by mid-Aptian organic-rich shales, marls, and sandstones [11] of probable lacustrine origin.
The evaporites and interbedded lacustrine shales thin northward and have not been penetrated by drilling in the northernmost part of the Douala sub-basin. However, diapiric evaporites were penetrated in the Kribi Marine-1 well in offshore Cameroon [12] in the Kribi-Campo Basin [2] .
Middle Albian to Cenomanian cyclic, shallowing-upward units of oolitic limestone and calcarenite from 5 to 15 m thick make up the shelf-carbonate rocks in the Rio Muni Basin [13] . In the Kribi-Campo sub-basin, shelf carbonates are similar to the Rio Muni carbonate rocks and are represented by carbonate rocks in the Mengo Formation, whereas in the Douala sub-basin, the Mungo Formation lacks massive shelf-carbonate rocks.
Progradational marine sedimentation that included the development of several Tertiary deltas, especially those of the Niger and Congo Rivers in the Niger Delta Province and West-Central Coastal Province, respectively, dominated the Cenozoic sedimentation. Resulting from this progradational phase was the deposition of regressive sandstones and siltstones, turbidites, and deep-marine shale units during the Paleocene and Eocene. In the Douala sub-basin, calcareous mudstones and marls were deposited in the Paleocene and Eocene [14] .
The Douala sub-basin is larger than the Rio del Rey basin, and contains a more continuous stratigraphic section. Continental basal Cretaceous sands are overlain by shallow marine limestones, sandstones and shales of Late Cretaceous, Palaeogene and Neogene ages. At the western margin of the basin these formations are overlain by basaltic lavas from the Cameroon volcanic centre. When traced offshore the sedimentary formations thicken markedly, with evidence for over 7 km of subsidence since the middle of the Cretaceous Period. There are more sands and fewer shales than in the Rio del Rey basin, and growth faulting and diapirism due to overpressured shales are largely absent [15] .
Products of volcanism (Miocene) are known to cover sediments in some area (e.g. Volcanic products of Mount Cameroon) [7] .
2.2. Tectonic Setting
The Cretaceous break-up of Gondwana and the separation of Africa from South America gave rise to the development of the Douala sub-basin. The initial rifting phase may have started during very Early Cretaceous time (Berriasian-Hauterivian) but the principal rifting episode in these areas occurred from late Barremian-Aptian time. During the late Aptian-late Albian interval, it is believed that the initial formation of oceanic crust began as the continents separated. The rifting would appear to have been asymmetrical, as many of the syn-rift features that would normally be expected are not apparent at depth in this area, whereas they are abundant in the corresponding South American segment. Several additional tectonic events occurred during the passive “drift” phase of the continental margin evolution at 84 Ma (Santonian), 65 Ma (Cretaceous/Tertiary boundary) and 37 Ma (late Eocene). These events, resulting in uplift, deformation and erosion at the basin margins, are generally attributed to changes in plate motion and intraplate stress fields due to convergent and collision events between Africa and Europe. The Santonian uplift and possibly the late Eocene events also appear to have resulted in significant mass wasting of the continental margin by gravity sliding, contributing towards reservoir formation. The final uplift event relates to the growth of the Cameroon Volcanic Line (CVL) and effectively lasts from 37 Ma through to present day on the northwest margin of the basin [1] .
3. Methodology and Results Obtained
3.1. Data Used
The gravity data set used in this study is constituted of 912 gravity data points located between longitudes 8˚10.2' to 10˚59.4'E and latitudes 2˚30.6' to 4˚59.4'N. The study area is the onshore portion of the Douala sub-basin which lies between longitudes 9˚ and 10˚ and latitudes 3.05˚ and 4.1˚; it contains about 116 gravity data points (Figure 1).
The Kriging method was applied on the gravity data for interpolation to obtain a 100 by 100 square grid having spacings of 0.0285 in longitude axis and 0.0250 in latitude axis. The Bouguer anomaly map (Figure 3) was then generated at a contour interval of 12 mGal (the mGal is the unit of acceleration due to gravity which is very practical to use in geophysics, 1 mGal = 0.01 m/s2). The study area is characterised by considerably high positive anomaly values especially towards the NW section of the study area with peak value of 104.1 mGals at longitude 9.2˚ and latitude 4.0˚ and coutours oriented mostly in the NNE direction.
3.2. The Residual Field
The different sources beneath the study area which characterize the Bouguer anomaly map can be identified by generating the residual field from the observed gravity field. This residual field is the result of estimating and extracting the more uniform regional field caused by sources situated at very great depths due to long wavelength anomalies of a regional scale across the entire area from the Bouguer anomaly field. The residual field is produced from more localised sources with short wavelengths which usually are found at shallow depths. The regional and residual fields were separated from the observed field by using the upward continuation method and also the analytical method by least squares, which generates the closest possible mathematical surface to the experimental surface [16] -[17] .
Since the gravity field obeys Lapace’s equation, it is therefore possible to apply continuation to it which is a process that permits the determination of a field over an arbitrary surface if the field is known completely over another surface and no masses are located between the two surface [18] .
Upward continuation is an operation that shifts the data by a constant height level above the surface of the earth (or the plane of measurement). It is used to estimate the large scale or regional (low frequency or long wave length) trends of the data [19] . Since upward continuation removes high frequency contents from data, it is similar to low-pass filtering.
Upward continuation can be formulated thus:
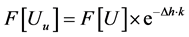 (1)
(1)
where  and
and 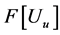 are the fourier transforms of the potential field
are the fourier transforms of the potential field 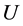 and upward potential field
and upward potential field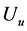 ,
,  is the elevation difference, and
is the elevation difference, and 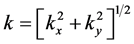 is the radial wave number [20] . The inverse Fourier transform of
is the radial wave number [20] . The inverse Fourier transform of 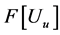 gives the transformed field
gives the transformed field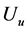 . The program Fourpot, version 1.3, by Markku Pirttijärvi [19] has been used to determine the upward continuation. The maximum that
. The program Fourpot, version 1.3, by Markku Pirttijärvi [19] has been used to determine the upward continuation. The maximum that 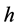 can take is equal to the optimum upward continuation height
can take is equal to the optimum upward continuation height 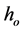 of the gravimetric field [21] .
of the gravimetric field [21] .
The empirical method of [22] has been used to obtain the optimum upward continuation height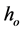 . This method consists of determining the Bouguer upward continuation height where the correlation between the upward continued fields at the successive heights presents a maximum deflection [23] . The following steps of data treatment were carried out to determine the optimum height ho in the present study area:
. This method consists of determining the Bouguer upward continuation height where the correlation between the upward continued fields at the successive heights presents a maximum deflection [23] . The following steps of data treatment were carried out to determine the optimum height ho in the present study area:
· Obtaining the upward continuation of Bouguer anomalies at heights from 5 to 120 km, by 5 km intervals.
· The calculation of correlation factors 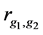 between the upward continued fields
between the upward continued fields 


where 



· Plotting the correlation factor as a function of increasing continuation height by making each correlation factor correspond to the lower of the two successive heights (Figure 4). The deflection at each height is given by the gap between the correlation factor curve and the line joining the two ends of the curve. The variation of the deflection with respect to the continuation height is presented in Figure 5. The maximum value on this curve which occurs at the height 
In the analytical method by least squares, the regional field of order 



A maximum correlation factor of 0.978581453 was obtained for an order of

The obtained residual field has been interpolated using the Kriging method to yield a 100 × 100 square grid with longitude and latitude spacings of 0.0285 and 0.0250. A residual field plot with a contour interval of 5 mGal was drawn from the grid (Figure 7).
Figure 4. Plot of correlation factor as a function of increasing continuation height.
Figure 5. Plot of the variation of deflection with respect to the continuation height.
This map presents our study area with the same characteristics as the Bouguer anomaly map but with picks of maximum value 90.02 mGals at longitude 9˚9.9' and latitude 4˚1' in the NW portion of the study area. This value is 14.09 mGal less than the peak value on the Bouguer anomaly map. The high gravity supposes a high density intrusive body in this zone which was studied along one profile (Figure 10). The density contrast of the intru-
Figure 6. Plot of the correlation factor between regional fields (from orders of polynomial and upward continuation) against polynomial orders from 
Figure 7. Residual field plot in the study area.
sive body was determined by the ideal body solution.
The residual field obtained here (using the upward continuation method which has been shown to be equivalent to the residual field from the analytical method of order 4) will be studied using the multi-scale horizontal derivative of the vertical derivative (MSHDVD) method (employed for the analysis of the multi-scale vertical derivative), the ideal body solution method, the spectral analysis method and the 2.5D modelling method in order to bring out the nature of the intrusive body.
3.3. Gravity Gradients
The vertical and/or horizontal derivatives of gravity fields have been used to obtain source parameters when interpreting gravity data [20] [25] -[27] . Horizontal gradient magnitude of the Bouguer gravity anomaly has been associated to the upward continuation of the field to characterize faults [28] . Nevertheless, an offset in the maximum of the horizontal gradient magnitude from a position directly above the geological contacts can occur; this can be the case when these contacts are not steep or when many of them are close to each other [29] . It is on this note that it has been proposed that more accurate results will be obtained when locating the contacts of sources in the case where the gravity fields of many sources interfere by using the vertical derivative of a field rather than the field itself [30] . One reason for this is the fact that the vertical derivative is able to isolate the gravity effects of individual sources better than the Bouguer anomaly. Therefore, the vertical derivative response can be used to identify and map the signatures of small scale features that are not easily identified on Bouguer anomaly maps [21] . Using the vertical derivative has a shortcoming in that it can amplify short wavelength noise coming from poor data processing and/or from local subsurface density variations not corrected for. This shortcoming can be overcome by making use of the multi-scale vertical derivative in the multi-scale horizontal derivative of the vertical derivative (MSHDVD) method in which for a vertical derivative, a corresponding horizontal derivative magnitude is used to differentiate between vertical and dipping geological contacts and also the direction of the dip [21] .
The MSHDVD method entails the following three steps:
1) Calculating the first-order vertical derivative for upward continued gravity field at different heights, called here the MSVD (multi-scale vertical derivative);
2) Determining the maxima of the horizontal gradient of the MSVD;
3) Superposing the maps obtained for different continuation heights.
In this study, the method of finite differences proposed by [31] has been used to obtain the first-order vertical derivative of the gravity field at each height in the space domain. This is more stable than the continuation in the frequency domain [32] , which in some cases enhances data errors, depending on the signal/noise ratio. Another advantage of this is that it allows the calculation of the vertical derivative at several heights, using a stable operator like upward continuation [33] .
The vertical derivative 


where 








The first-order vertical derivative of the gravity field was therefore obtained at heights of 5, 10, 15, 20, 25 and 30 km.
The (local) maxima of the horizontal gradient of the vertical derivative 

The Blakely and Simpson [20] method was used to determine positions of local maxima and by using the BOUNDARY program of the Fortran 77 package of the United States Geological Survey [34] the horizontal gradients and their maxima were obtained [23] . The Horizontal derivatives/gradients and consequently the maxima of the horizontal gradients were calculated with significant level N = 2 [20] for all the upward continued heights above.
These maxima of horizontal gradient determined from the vertical derivative of the Bouguer anomalies were superimposed to give the plot on the map in Figure 8.
This plot does not contain any emphasis of quasi-linear contacts, which can describe faults and quasi-circular contacts corresponding to horizontal limits of intrusive bodies. It can therefore be considered that no fault lines cut across this zone; but the presence of local maxima spread across the region can suggest the presence of a body with horizontal variation in surface height but whose boundaries extend beyond this zone of study or which lies on a broader body of similar density.
3.4. Spectral Analysis for Source-Depth Estimation
The program Fourpot version 1.3 [19] has been used to calculate the radial amplitude spectrum of the residual at upward continuation height of 30 km as a function of radial wave-number

along rings with radius 


transform of the potential field in the frequency domain.
The amplitude spectrum was used to estimate the depth 




Results of spectral analysis carried on the residual at upward continued height of 30 km suggest that the depth of the potential field source is about 4.8 km. This can be seen on Figure 9.
3.5. Ideal Body Solution
The theory of ideal bodies was originally developed by Parker [35] -[36] . This theory characterizes the extremal
Figure 8. Plot of the maxima of horizontal gradient determined from the vertical derivative of the Bouguer anomalies. Colour legend: Yellow = 5 km, Pink = 10 km, Green = 15 km, Red = 20 km, Blue = 25 km, Brown = 30 km.
Figure 9. Radial amplitude spectrum with one manually fitted line having a slope of 4.753 km which is an estimate of the depth of the potential field source.
solution with the smallest possible maximum density which greatly helps in the fundamental problem of non-uniqueness encountered in the interpretation of gravity anomaly data even when the solution set is bounded by physical or geologic constraints.
The basic philosophy behind this theory is that when a data set admits an infinite solution set, as the case is with potential fields like the gravity field, properties common to all solutions are sought and as such definite information about the unknown true solution is derived.
For gravity data specifically, bounds on the uniform norm or maximum absolute value of the density contrast of the source were treated by Parker. When a data set and a region in which a source is confined are considered, there exists a unique solution with the smallest possible uniform bound. This source is attributed the term “ideal body” for all possible sources in that region of confinement and its norm is the greatest bound on the maximum absolute value of all sources fitting the data. Consequently, any solution (as well as true one) must somewhere reach or exceed this bound.
The theory of ideal problems has been applied to different disciplines like to gravity data [37] -[41] , magnetic data [42] , heat-flow data [43] -[45] , and static earth displacement [46] .
Gravity ideal-body analysis is an excellent reconnaissance exploration tool because it is especially well suited for handling sparse data contaminated with noise, for finding useful, rigorous bounds on the infinite solution set, and for predicting accurately what data need to be collected in order to tighten those bounds [47] .
Analytical solutions for ideal bodies can only be constructed for two data [35] . On a flat terrain, two data values yields a 2-D solution which is a horizontal half-cylinder and the 3-D solution which is a hemisphere. Since no analytical method exists to solve for ideal bodies or, more importantly, the associated density bound when more than two data are used, a good numerical approximation to the solution of ideal bodies can be obtained for an arbitrary number of data using the linear programming approximation which involves partitioning the region of confinement into a large number of cells, each of constant density. The linear programming algorithm assigns densities to the cells such that the data are satisfied, and the maximum density is as small as possible.
In this study, the program, IDB2 developed by Huestis and Ander [40] capable of treating up to 500 cells has been used to obtain the ideal body solution along a 65 km NW-SE profile (PP’) (Figure 10) using the following six (6) sets of distance (in km) and gravity anomaly (in mGal) points: (3.93, 44.39), (14.66, 62.23), (25.33, 80.98), (36.01, 84.05), (46.83, 53.75), (59.09, 34.05).
The program IDB2 was used in an initial run such that the ideal body touches the bottom of the volume (this is the point at which any further increase in depth does not change the ideal body and the value of the density contrast).
This indicates the greatest lower bound on the density contrast of the source which is equal to 0.266 g/cm3 (see Figure 11). This information is plotted as the first point on both tradeoff curves of Figure 12 and Figure 13.
Figure 10. Map of residual field of study zone showing NW-SE profile (PP'). The accumulated distance in the cross section of the profile represents the distance from P to P' along the profile.
Figure 11. Ideal body plot when it is touching both the surface and bottom of the region of confinement. The greatest lower bound on the density contrast of the source is given to be equal to 0.266 g/cm3. (Horizontal axis is distance in km along profile, vertical axis is depth in km with negative sign signifying depth increases downward, the scale takes values in g/cm3).
Figure 12. Two-dimensional gravity ideal-body tradeoff curves for profile PP' (plot of density contrast against thickness of ideal body when it is kept to touch the surface of the region of study and its thickness is systematically reduced).
Figure 13. Two-dimensional gravity ideal-body tradeoff curves for profile PP' (plot of density contrast against depth to top of ideal body when the top of the confining region is then pushed down below the surface while not bounding the bottom of the ideal body from below).
From this point, the maximum allowable thickness of the body is confined such that it reduces systematically. The values of increasing density contrasts are plotted for corresponding decreasing values of thickness on the first tradeoff curve (Figure 12) yielding a curve which indicates the least possible maximum density contrast allowed by the data set, which is 0.266 g/cm3. This curve also gives the minimum thickness of the ideal body at the point where the density contrast is considered to have its maximum value. From Koumetio [48] , it is suggested that this region of the Douala sub-basin has an intrusion of igneous rocks beneath it. Considering the density values of igneous rocks (with that of Gabro = 3.03 g/cm3 and Peridotite = 3.15 g/cm3 being among the highest) and the average density value of sedimentary rocks equal to 2.5 g/cm3; the maximum geological reasonable density contrast in this region is taken to be 0.65 g/cm3. Taking this value of maximum density contrast into consideration, the minimum thickness of the ideal body is given to be 5.1 km.
The top of the confining region is then pushed down below the surface while not bounding the bottom of the ideal body from below. The top is pushed down until the density far exceeds any geologically reasonable density contrast. The values of density contrasts obtained are plotted against values of depth to top of body to give the second tradeoff curve (Figure 13) from which, at the point of maximum density contrast (0.65 g/cm3), the maximum depth to the top of the ideal body is given as 11.5 km. This tradeoff curve gives the greatest lower bound on the maximum density contrast versus the depth to the top of the body, or alternately, the maximum density contrast versus the least upper bound on the depth to the top of the body [47] .
3.6. Modeling
2.5D modelling was carried out on the residual field obtained in this region along the NW-SE profile (PP’) aimed at bringing out the structure of the intrusive body contained below this study area.
The program GRAV2DC [49] has been used to carry out the modelling. GRAV2DC offers the possibility to interactively design a geological model in the form of a polygon whose gravity signature correlates with the observed anomalies. The value of the density contrast (0.266 g/cm3) obtained from the ideal body solution; the result of spectral analysis and the result of multi-scale analysis of the maxima of gradients were used as constraints in the modelling process to carry out the 2.5D modelling which resulted in a model for the intrusive body. This model consist of a major block having a density contrast of 0.266 g/cm3, a depth of 5.9 km to its surface, lateral extensions of 32 Km in perpendicular directions to the profile PP’ and a depth of 32.8 km to its base (Figure 14).
To the left of this major block is a very thin elongated block of density contrast 0.266 g/cm3 at a depth of 6.8 km overlying another thin block of density 0.106 g/cm3. Similarly, to the right of the major block is another very thin elongated block of density contrast 0.266 g/cm3 at a depth of 5.3 km overlying another thin block of density 0.0617 g/cm3.
Figure 14. 2.5D model from the NW-SE Profile PP' showing in the lower section a major block with density contrast = 0.266 g/cm3 at a depth of 5.9 km and other minor blocks to its left and right at depths of 6.8 km and 5.3 km respectively. The white background represents a milieu of sedimentary rocks. In the upper section of the figure, asterisks represent observed field while smooth line represents calculated field.
4. Discussion of Results
The high gravity values noticed in the NW portion of the area studied in this work on both the Bouguer anomaly and the residual anomaly maps (Figure 3 and Figure 7) when studied for their gravimetric subsurface structure present a considerable good match between the observed field and the calculated field in its 2.5D model (Figure 14). The constraints used for this modelling included the results of spectral analysis which suggested that the depth of the potential field source is about 4.8 km; the results of the multi-scale analysis of the maxima of gradients which presented no clear cut or distinct quasi-linear contacts or quasi-circular contacts; and the results of ideal body solution (inverse method) which suggested an ideal body with density contrast (being the smallest possible maximum density contrast [35] -[36] ) of 0.266 g/cm3, minimum thickness of 5.1 km and the maximum depth of 11.5 km to its top. The 2.5D model of the intrusive body obtained in this study greatly agrees with these suggestions since it has a density contrast of 0.266 g/cm3 and its top lies at a depth of about 5.9 km which is slightly greater than the value of 4.8 km suggested by spectral analysis and considerably lesser than the maximum value of 11.5 km suggested by the ideal body solution. The body also has an average thickness of about 27 km (with its base lying at about 32.8 km) which is in agreement with the suggestion by the ideal body solution that the minimum thickness of the body is 5.1 km. This model of the intrusive body in its alignment is not completely vertical, but elongates and varies horizontally; this might possibly explain why the results of the multi-scale analysis of the maxima of gradients do not present major quasi-linear contacts or quasi-circular contacts. But by considering that the edges of the body are almost vertical at different step-like positions and the body has a base at a depth of about 32.8 km which is almost at the crust-mantle boundary [3] , it is possible that the absence of these contacts in the multi-scale analysis of the maxima of gradients is as a result of the fact that this body directly sits on a more broadly spread body of almost same density which possibly could be a slightly uplifted half-dome mantle formation [48] . Since the Douala sub-basin is a sedimentary basin, for which analysis in this study have been carried out considering its rocks to have an average density of 2.5 g/cm3 [18] , it implies that with the obtained density contrast of 0.266 g/cm3, the intrusive body which is of igneous origin will have a density of about 2.77 g/cm3. When the density range of igneous rocks is considered, it is possible that the intrusive body in this study area could be andesite (2.4 - 2.8 g/cm3), granite (2.50 - 2.81 g/cm3), granodiorite (2.67 - 2.79 g/cm3), porphyry (2.60 - 2.89 g/cm3), Quartz diorite (2.62 - 2.96 g/cm3), Diorite (2.72 - 2.99 g/cm3), Diabase (2.50 - 3.20 g/cm3), Basalt (2.70 - 3.30 g/cm3), Gabbro (2.70 - 3.50 g/cm3), Acid igneous (2.30 - 3.11 g/cm3), syenite (2.60 - 2.95 g/cm3) or Basic igneous (2.09 - 3.17 g/cm3) [18] [50] -[51] . Therefore, the 2.5D model possibly consists of an igneous intrusive body surrounded by sedimentary formations.
5. Conclusion
In this study, gravity data have been processed for Bouguer anomaly and residual fields in the NW portion of the Douala sub-basin along a 65 km NW-SE profile (PP') using the method of upward continuation with correlated results from the polynomial analytical method. 2.5 D modelling on data along this profile was carried out by considering the results obtained from spectral analysis, the multi-scale analysis of the maxima of gradients, and the inverse method of the ideal body solution as constraints; this 2.5 D modelling presents a source body which is very probably an intrusive igneous block in a sedimentary background having a density contrast of 0.266 g/cm3 and consequently a density of 2.77 g/cm3 when the average density of the surrounding sedimentary rocks is taken to be 2.5 g/cm3. The inclusion of more data points in the data used in this work which will lead to a reduced spacing between data points and the application of other methods of survey like the seismic method will surely bring in more details and information concerning the structure of the underlying intrusive igneous body in this region.
Acknowledgements
The very useful technical assistance of Ngatchou Evariste and the insightful contributions of Alain-Pierre K. Tokam which have led to the considerable amelioration of this work and the eventual realisation of this paper cannot be over emphasized. They are deeply acknowledged.
References
- Kenfack, P.L., Njike, P.R.N., Ekodeck, G.E. and Ngueutchoua, G. (2012) Fossils Dinoflagellates from the Northern Border of the Douala Sedimentary Sub-Basin (South-West Cameroon): Age Assessment and Paleoecological Interpretations. Geosciences, 2, 117-124. DOI: 10.5923/j.geo.20120205.03
- Brownfield, M.E. and Charpentier, R. R. (2006) Geology and Total Petroleum Systems of the West-Central Coastal Province (7203), West Africa. US Geological Survey Bulletin 2207-B. http://www.usgs.gov/bul/2207/B/
- Tokam, K.A.P., Tabod, C.T., Nyblade, A.A., Julia, J., Wiens, D.A. and Pasyanos, M. (2010) Structure of the Crust Beneath Cameroon, West Africa, from the Join Inversion of Rayleigh Wave Group Velocities and Receiver Functions. Geophysical Journal International, 183, 1061-1076. http://dx.doi.org/10.1111/j.1365-246X.2010.04776.x
- Ndikum, E.N., Tabod, C.T. and Tokam, A.-P.K. (2014) Frequency Time Analysis (FTAN) and Moment Tensor Inversion Solutions from Short Period Surface Waves in Cameroon (Central Africa). Open Journal of Geology, 4, 33-43. http://dx.doi.org/10.4236/ojg.2014.42004
- Ndikum, E.N., Tabod, C.T., Tokam, A.-P.K. and Essimbi, B.Z. (2014) Fault-Plane Solution of the Earthquake of 19 March 2005 in Monatele (Cameroon). Open Journal of Geology, 4, 289-293. http://dx.doi.org/10.4236/ojg.2014.46021
- Ngon, G.F.N., Etame, J., Ntamak-Nida, M.J., Mbog, M.B., Mpondo, A.M.M., Martine, G., Yongue-Fouateu, R. and Bilong, P. (2012) Geological Study of Sedimentary Clayey Materials of the Bomkoul Area in the Douala Region (Douala Sub-Basin, Cameroon) for the Ceramic Industry. C. R. Geoscience, 344, 366-376. http://dx.doi.org/10.1016/j.crte.2012.05.004
- Kenfack, P.L., Ngaha, P.R.N., Ekodeck, G.E. and Ngueutchoua, G. (2012) Mineralogic Characterization and Petroleum Potential of Clays (Shales) of the N’Kapa Formation (Paleocene-Eocene) in the Douala Sedimentary Sub-Basin (South-West Cameroon). International Journal of Geosciences, 3, 696-709. http://dx.doi.org/10.4236/ijg.2012.34070
- Nguene, F.R., Tamfu, S., Loule, J.P. and Ngassa, C. (1992) Paleoenvironnements of the Douala and Kribi/Campo Sub- Basins in Cameroon, West African. Géologie Africaine: Colloque de Géologie Africaine, Libreville, Recueil des Com- munications, 6-8 May 1991, 129-139.
- Regnoult, J.M. (1986) Synthèse Gélogique du Cameroun. D.M.G, Yaoundé, Cameroun, 118 p.
- SNH/UD (2005) Stratigraphie Séquentielle et Tectonique des Dépôts Mésozoїques Syn-Rifts du Bassin de Kribi/ Campo. Rapport Non Publié, 134 p.
- Ross, D. (1993) Geology and Hydrocarbon Potential of Rio Muni Area, Equatorial Guinea. Oil and Gas Journal, 91, 96-100.
- Pauken, R.J. (1992) Sanaga Sud Field, Offshore Cameroon, West Africa. In: Halbouty, M.T., Ed., Giant Oil and Gas Fields of the Decade 1978-1988, American Association of Petroleum Geologists Memoir, Tulsa, 217-230.
- Turner, J.P. (1995) Gravity-Driven Structures and Rift Basin Evolution: Rio Muni Basin, Offshore West Africa. Ame- rican Association of Petroleum Geologists Bulletin, 79, 1138-1158.
- Coward, M.P., Purdy, E.G., Ries, A.C. and Smith, D.G. (1999) The Distribution of Petroleum Reserves in Basins of the South Atlantic Margins. In: Cameron, N.R., Bate, R.H. and Clure, V.S., Eds., The Oil and Gas Habitats of the South Atlantic, Geological Society (London) Special Publication, London, 101-131.
- Selley, R.C. (1997) African Basins, Sedimentary Basins of the World. 3rd Edition, Elsevier Science B.V., Amsterdam, 173-186.
- Abdelrahman, E.M., Riad, S., Refai, E. and Amin, Y. (1985) On the Least-Squares Residual Anomaly Determination. Geophysics, 50, 473-480. http://dx.doi.org/10.1190/1.1441925
- Radhakrishna, I.V. and Krishnamacharyulu, S.K.G. (1990) Polyfit: A Fortran 77 Program to Fit a Polynomial of Any Order to Potential Field Anomalies. Journal of Association of Exploration Geophysicists, 11, 99-105.
- Telford, W.M., Geldart, L.P. and Sheriff, R.E. (1990) Applied Geophysics. 2nd Edition, Cambridge University Press, Cambridge, 6-61.
- Pirttijärvi, M. (2009) FOURPOT. Department of Physics, University of Oulu, Oulu, Geophysics. http://www.cc.oulu.fi/∼mpi/softat/Fourpot.html
- Blakely, R.J. and Simpson, R.W. (1986) Approximating Edges of Source Bodies from Magnetic or Gravity Anomalies. Geophysics, 51, 1494-1498. http://dx.doi.org/10.1190/1.1442197
- Noutchogwe, T.C., Tabod, C.T., Koumetio, F. and Manguelle-Dicoum, E. (2011) A Gravity Model Study for Differentiating Vertical and Dipping Geological Contacts with Application to a Bouguer Gravity Anomaly over the Foumban Shear Zone, Cameroon. Geophysica, 47, 43-55.
- Zeng, H., Xu, D. and Tan, H. (2007) A Model Study for Estimating Optimum upward Continuation Height for Gravity Separation with Application to a Bouguer Gravity Anomaly over a Mineral Deposit, Jilin Province, Northeast China. Geophysics, 72, 145-150. http://dx.doi.org/10.1190/1.2719497
- Koumetio, F., Njomo, D., Tabod, C.T., Noutchogwe T.C. and Manguelle-Dicoum, E. (2012) Structural Interpretation of Gravity Anomalies from the Kribi-Edea Zone, South Cameroon: A Case Study. Journal of Environmental & Engineering, 9, 664-673.
- Abdelrahman, E.M., Bayoumi, A.I., Abdelhady, Y.E., Gobashi, M.M. and El-Raby, H.M. (1989) Gravity Interpretation Using Correlation Factors between Successive Least-Squares Residual Anomalies. Geophysics, 54, 1614-1621. http://dx.doi.org/10.1190/1.1442629
- Cordell, L. (1979) Gravimetric Expression of Graben Faulting in Santa Fe Country and the Espanola Basin, New Mexico. Guidebook to Santa Fe Country. In: Ingersoll, R.V., Ed., New Mexico Geological Society Guidebook: 30th Field Conference, 59-64.
- Cordell, L. and Grauch, V.J.S. (1985) Mapping Basement Magnetization Zones from Aeromagnetic Data in the San Juan Basin, New Mexico. In: Hinze, W.J., Ed., The Utility of Tegional Gravity and Magnetic Anomaly Maps, Society of Exploration Geophysicists, Tulsa, 181-197.
- Marson, I. and Klingele, E.E. (1993) Advantages of Using the Vertical Gradient of Gravity for 3-D Interpretation. Ge- ophysics, 58, 1588-1595. http://dx.doi.org/10.1190/1.1443374
- Khattach, D., Keating, P., Mostafa, M.L., Chennouf, T., Andrieux, P. and Milhi, A. (2004) Apport de la gravimétrie à l’étude de la structure du bassin des Triffa (Maroc nord-oriental): Implications hydrogéologiques. Comptes Rendus Ge- oscience, 336, 1427-1432. http://dx.doi.org/10.1016/j.crte.2004.09.012
- Grauch, V.J.S. and Cordell, L. (1987) Limitations of Determining Density or Magnetic Boundaries from the Horizontal Gradient of Gravity or Pseudogravity Data. Geophysics, 52, 118-121. http://dx.doi.org/10.1190/1.1442236
- Fedi, M. and Florio, G. (2001) Detection of Potential Fields Source Boundaries by Enhanced Horizontal Derivative Method. Geophysical Prospecting, 49, 40-58. http://dx.doi.org/10.1046/j.1365-2478.2001.00235.x
- Florio, G., Fedi, M. and Pasteka, R. (2006) On the Application of Euler Deconvolution to the Analytic Signal. Geophy- sics, 71, L87-L93. http://dx.doi.org/10.1190/1.2360204
- Gunn, P.J. (1975) Linear Transformation of Gravity and Magnetic Fields. Geophysical Prospecting, 23, 300-312. http://dx.doi.org/10.1111/j.1365-2478.1975.tb01530.x
- Jacobsen, B.H. (1987) A Case for Upward Continuation as a Standard Separation Filter for Potential-Field Maps. Ge- ophysics, 52, 1138. http://dx.doi.org/10.1190/1.1442378
- Phillips, J.D. (1997) Potential-Field Geophysical Software for the PC, Version 2.2. US Geological Survey Open-File Report 97-725, 34.
- Parker, R.L. (1974) Best Bounds on Density and Depth from Gravity Data. Geophysics, 39, 644-649. http://dx.doi.org/10.1190/1.1440454
- Parker, R.L. (1975) The Theory of Ideal Bodies for Gravity Interpretation. Geophysical Journal International, 42, 315- 334. http://dx.doi.org/10.1111/j.1365-246X.1975.tb05864.x
- Safon, C., Vasseur, G. and Cuer, M. (1977) Some Applications of Linear Programming to the Inverse Gravity Problem. Geophysics, 42, 1215-1229. http://dx.doi.org/10.1190/1.1440786
- Ander, M.E. (1980) Geophysical Study of the Crust and Upper Mantle beneath the Rio Grande Rift and Adjacent Great Plains and Colorado Plateau. Ph.D. Thesis, University of New Mexico, Albuquerque/ Los Alamos National Laboratory Reo, Los Alamos, LA-8676-T.
- Ander, M.E. and Huestis, S.P. (1982) Mafic Intrusion beneath the Zuni-Bandera Volcanic Field, New Mexico. Geolo- gical Society of America Bulletin, 3, 1142-1150. http://dx.doi.org/10.1130/0016-7606(1982)93<1142:MIBTZV>2.0.CO;2
- Huestis, S.P. and Ander, M.E. (1983) IDB2—A Fortran Program for Computing Extremal Bounds in Gravity Data Interpretation. Geophysics, 48, 999-1010. http://dx.doi.org/10.1190/1.1441525
- Luyendyk, B.P. (1984) On-Bottom Gravity Profile across the East Pacific Rise at 21 North. Geophysics, 49, 2166- 2177. http://dx.doi.org/10.1190/1.1441632
- Huestis, S.P. and Parker, R.L. (1977) Bounding the Thickness of the Ocean Magnetized Layer. Journal of Geophysical Research, 82, 5293-5303. http://dx.doi.org/10.1029/JB082i033p05293
- Huestis, S.P. (1979) Extremal Temperature Bounds from Surface Gradient Measurements. Geophysical Journal International, 58, 249-260. http://dx.doi.org/10.1111/j.1365-246X.1979.tb01023.x
- Huestis, S.P. (1981) Temperature Bounds from Heat Flow Data on Irrerular Non-Isothermal Surfaces. Geophysical Journal International, 65, 165-170. http://dx.doi.org/10.1111/j.1365-246X.1981.tb02706.x
- Huestis, S.P. (1984) The Inverse Problem for Heat Flow Data in the Presence of Thermal Conductivtty Variations. Ge- ophysical Journal International, 78, 119-137. http://dx.doi.org/10.1111/j.1365-246X.1984.tb06475.x
- Vasco, D.W., and Johnson, L.R. (l985) Extremal Inversion of Static Earth Displacement Due to Volume Sources. Ge- ophysical Journal International, 80, 223-239.
- Ander, M.E. and Huestis, S.P. (1987) Gravity Ideal Bodies. Geophysics, 52, 1265-1278.
- Koumetio, F., Tabod, C.T. and Manguelle-Dicoum, E. (2009) Evidence for upper Mantle Intrusion in the West African Coastal Sedimentary Basins from Gravity Data: The Case of the Southern Part of the Douala Basin, Cameroon. Global Journal of Geological Sciences, 7, 181-187.
- Cooper, G.R.J. (1998) GRAV2DC for Windows User’s Manual (Version 2.05). Geophysics Department, University of the Witwatersrand, Johannesburg.
- (2014) Rock Property Tables for Specific Gravity, Density and Porosity. EduMine On-Line Bulletin. http://www.edumine.com/tools/rock-property-tables-for-specific-gravity-density-and-porosity/
- (2014) Rock Density Chart in Imgarcade. On-Line Image Arcade. http://imgarcade.com/1/rock-density-chart/
NOTES
*Corresponding author.
















