Open Journal of Discrete Mathematics
Vol.06 No.02(2016), Article ID:65377,8 pages
10.4236/ojdm.2016.62007
Computation of Topological Indices of Dutch Windmill Graph
M. R. Rajesh Kanna1, R. Pradeep Kumar2, R. Jagadeesh3
1Post Graduate Department of Mathematics, Maharani’s Science College for Women, Mysore, India
2Department of Mathematics, The National Institute of Engineering, Mysore, India
3Research and Development Centre, Bharathiar University, Coimbatore, India

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 January 2016; accepted 5 April 2016; published 8 April 2016
ABSTRACT
In this paper, we compute Atom-bond connectivity index, Fourth atom-bond connectivity index, Sum connectivity index, Randic connectivity index, Geometric-arithmetic connectivity index and Fifth geometric-arithmetic connectivity index of Dutch windmill graph.
Keywords:
ABC Index, ABC4 Index, Sum Connectivity Index, Randic Connectivity Index, GA Index, GA5 Index

1. Introduction
The Dutch windmill graph is denoted by  and it is the graph obtained by taking m copies of the cycle
and it is the graph obtained by taking m copies of the cycle 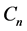 with a vertex in common. The Dutch windmill graph is also called as friendship graph if
with a vertex in common. The Dutch windmill graph is also called as friendship graph if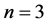 . i.e., friendship graph is the graph obtained by taking m copies of the cycle
. i.e., friendship graph is the graph obtained by taking m copies of the cycle 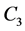 with a vertex in common. Dutch windmill graph
with a vertex in common. Dutch windmill graph 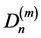 contains
contains 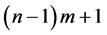 vertices and mn edges as shown in the Figures 1-3.
vertices and mn edges as shown in the Figures 1-3.
All graphs considered in this paper are finite, connected, loop less and without multiple edges. Let 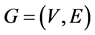 be a graph with n vertices and m edges. The degree of a vertex
be a graph with n vertices and m edges. The degree of a vertex 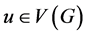 is denoted by
is denoted by 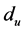 and is the number of vertices that are adjacent to u. The edge connecting the vertices u and v is denoted by uv. Using these terminologies, certain topological indices are defined in the following manner.
and is the number of vertices that are adjacent to u. The edge connecting the vertices u and v is denoted by uv. Using these terminologies, certain topological indices are defined in the following manner.
Topological indices are numerical parameters of a graph which characterize its topology and are usually graph invariants.
The atom-bond connectivity index, ABC index was one of the degree-based molecular descripters, which was introduced by Estrada et al. [1] in late 1990’s. Some upper bounds for the atom-bond connectivity index of
Figure 1.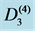 .
.
Figure 2. .
.
Figure 3.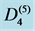 .
.
graphs can be found in [2] , The atom-bond connectivity index of chemical bicyclic graphs and connected graphs can be seen in [3] [4] . For further results on ABC index of trees, see the papers [5] - [8] and the references cited there in.
Definition 1.1. Let 

of G is defined as,
The fourth atom bond connectivity index, 

Definition 1.2. Let G be a graph, then its fourth ABC index is defined as, 
where 

for
The first and oldest degree based topological index was Randic index [12] denoted by 
Definition 1.3. For the graph G Randic index is defined as,
Sum connectivity index belongs to a family of Randic like indices. It was introduced by Zhou and Trinajstic [13] . Further studies on Sum connectivity index can be found in [14] [15] .
Definition 1.4. For a simple connected graph G, its sum connectivity index 

The Geometric-arithmetic index, 
Definition 1.5. Let G be a graph and 

The fifth Geometric-arithmetic index, 
Definition 1.6. For a Graph G, the fifth Geometric-arithmetic index is defined as
Where 

2. Main Results
Theorem 2.1. The Atom bond connectivity index of Dutch windmill graph is
Proof. Consider the Dutch windmill graph







We know that
i.e.,
□Theorem 2.2. The Randic Index of Dutch windmill graph is 
Table 1. Edge partition based on degrees of end vertices of each edge.
Figure 4.
i.e.,

Theorem 2.3. The Geometric-arithmetic index (GA) of Dutch windmill graph is

Proof. We know that

Theorem 2.4. The Sum connectivity index 

Proof. We know that
i.e.,

Theorem 2.5. The fourth atom bond connectivity index of Dutch windmill graph is
Proof. Any Dutch windmill graph 







Case (1) If







We know that
i.e.,
Figure 5.
Table 2. Edge partition based on degree sum of neighbors of end vertices of each edge.
Case (2) If



We know that
i.e.,
Theorem 2.6. The fifth Geometric-arithmetic index (
Proof. We know that
Case (1) If

2 and Figure 5]
Case (2) If
Table 3. Edge partition based on degree sum of neighbors of end vertices of each edge.
[From Table 3]

3. Conclusion
The problem of finding the general formula for ABC index, 

Acknowledgements
The first author is also thankful to the University Grants Commission, Government of India for the financial support under the grant MRP(S)-0535/13-14/KAMY004/UGC-SWRO.
Conflict of Interests
The authors declare that there are no conflicts of interests regarding the publication of this paper.
Cite this paper
M. R. Rajesh Kanna,R. Pradeep Kumar,R. Jagadeesh, (2016) Computation of Topological Indices of Dutch Windmill Graph. Open Journal of Discrete Mathematics,06,74-81. doi: 10.4236/ojdm.2016.62007
References
- 1. Estrada, E., Torres, L., Rodriguez, L. and Gutman, I. (1998) An Atom-Bond Connectivity Index: Modelling the Enthalpy of Formation of Alkanes. Indian Journal of Chemistry, 37A, 849-855.
- 2. Chen, J., Liu, J. and Guo, X. (2012) Some Upper Bounds for the Atom-Bond Connectivity Index of Graphs. Applied Mathematics Letters, 25, 1077-1081.
http://dx.doi.org/10.1016/j.aml.2012.03.021 - 3. Chen, J. and Guo, X. (2012) The Atom-Bond Connectivity Index of Chemical Bicyclic Graphs. Applied Mathematics— A Journal of Chinese Universities, 27, 243-252.
http://dx.doi.org/10.1007/s11766-012-2756-4 - 4. Xing, R., Zhou, B. and Dong, F. (2011) On Atom-Bond Connectivity Index of Connected Graphs. Discrete Applied Mathematics, 159, 1617-1630.
http://dx.doi.org/10.1016/j.dam.2011.06.004 - 5. Furtula, B., Gravoc, A. and Vukicevic, D. (2009) Atom-Bond Connectivity Index of Trees. Discrete Applied Mathematics, 157, 2828-2835.
http://dx.doi.org/10.1016/j.dam.2009.03.004 - 6. Gutman, I., Furtula, B. and Ivanovic, M. (2012) Notes on Trees with Minimal Atom-Bond Connectivity Index. MATCH Communications in Mathematical and in Computer Chemistry, 67, 467-482.
- 7. Xing, R., Zhou, B. and Du, Z. (2010) Further Results on Atom-Bond Connectivity Index of Trees. Discrete Applied Mathematics, 157, 1536-1545.
http://dx.doi.org/10.1016/j.dam.2010.05.015 - 8. Xing, R. and Zhou, B. (2012) Extremal Trees with Fixed Degree Sequence for Atom-Bond Connectivity Index. FILOMAT, 26, 683-688.
http://dx.doi.org/10.2298/FIL1204683X - 9. Ghorbani, M. and Hosseinzadeh, M.A. (2010) Computing ABC4 Index of Nanostar Dendrimers. Optoelectronics and Advanced Materials: Rapid Communications, 4, 1419-1422.
- 10. Farahani, M.R. (2013) Computing Fourth Atom-Bond Connectivity Index of V-Phenylenic Nanotubes and Nanotori. Acta Chimica Slovenica, 60, 429-432.
- 11. Farahani, M.R. (2013) On the Fourth Atom-Bond Connectivity Index of Armchair Polyhex Nanotube. Proceedings of the Romanian Academy—Series B, 15, 3-6.
- 12. Randic, M. (1975) On Characterization of Molecular Branching. Journal of the American Chemical Society, 97, 6609-6615.
http://dx.doi.org/10.1021/ja00856a001 - 13. Zhou, B. and Xing, R. (2011) On Atom-Bond Connectivity Index. Zeitschrift für Naturforschung, 66a, 61-66.
http://dx.doi.org/10.5560/ZNA.2011.66a0061 - 14. Zhou, B. and Trinajstic, N. (2009) On a Novel Connectivity Index. Journal of Mathematical Chemistry, 46, 1252-1270.
http://dx.doi.org/10.1007/s10910-008-9515-z - 15. Zhou, B. and Trinajstic, N. (2010) On General Sum-Connectivity Index. Journal of Mathematical Chemistry, 47, 210-218.
http://dx.doi.org/10.1007/s10910-009-9542-4 - 16. Vukicevic, D. and Furtula, B. (2009) Topological Index Based on the Ratios of Geometrical and Arithmetical Means of End-Vertex Degrees of Edges. Journal of Mathematical Chemistry, 46, 1369-1376.
http://dx.doi.org/10.1007/s10910-009-9520-x - 17. Chen, S. and Liu, W. (2010) The Geometric-Arithemtic Index of Nanotubes. Journal of Computational and Theoretical Nanoscience, 7, 1993-1995.
http://dx.doi.org/10.1166/jctn.2010.1573 - 18. Das, K.C. and Trinajstic, N. (2010) Comparision between First Geometric-Arithmetic Index and Atom-Bond Connectivity Index. Chemical Physics Letters, 497, 149-151.
http://dx.doi.org/10.1016/j.cplett.2010.07.097 - 19. Xiao, L., Chen, S., Guo, Z. and Chen, Q. (2010) The Geometric-Arithmetic Index of Benzenoidsystems and Phenylenes. International Journal of Contemporary Mathematical Sciences, 5, 2225-2230.
- 20. Graovac, A.. Ghorbani, M. and Hosseinzadeh, M.A. (2011) Computing Fifth Geometric-Arithmetic Index for Nanostar Dendrimers. Journal of Mahematical Nanoscience, 1, 33-42.













 [From
[From 

 [From
[From 

 [From
[From 













