Open Journal of Discrete Mathematics
Vol.4 No.3(2014), Article
ID:48296,12
pages
DOI:10.4236/ojdm.2014.43011
The Antimedian Function on Paths
Oscar Ortega, Yue Wang
Department of Mathematics, Harold Washington College, Chicago, IL, USA
Email: oortega@ccc.edu, yue.yale.wang@hotmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/
![]()


Received 20 May 2014; revised 19 June 2014; accepted 15 July 2014
ABSTRACT
An antimedian of a sequence 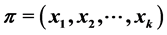 of elements of a finite metric space
of elements of a finite metric space 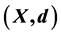 is an element
is an element  for which
for which 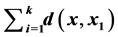 is a maximum. The function with domain the set of all finite sequences on
is a maximum. The function with domain the set of all finite sequences on![]() , and defined by
, and defined by 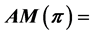 {
{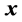 :
: is an antimedian of
is an antimedian of 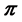 } is called the antimedian function on
} is called the antimedian function on![]() . In this note, the antimedian function on finite paths is axiomatically characterized.
. In this note, the antimedian function on finite paths is axiomatically characterized.
Keywords:Status, Location Function, Antimedian, Antimedian Function

1. Introduction
The problem of finding one optimal location for schools, drug stores, police stations, and hospitals requires facilities to be placed near the users in order to minimize, for example, the distance traveled to reach them. Location theory deals with this type of optimization problem. Location functions such as the median, the center, and the mean have been used to solve these type of problems. On the other hand, there are circumstances where placing one or more facilities as far as possible from the users is the best solution. For instance, it is necessary to locate nuclear power plants far from cities or towns to minimize the risk of radiation problems. Similar problems include the determination of suitable locations for observatories, radio stations, airports, and chemical plants. The solution to the problem of finding an optimal location for these types of obnoxious facilities on networks has been studied by Church and Garfinkel [1] , Minieka [2] , Ting [3] , and Zelinka [4] . In these investigations two solutions to the problem are given from an algorithmic perspective. The most appealing solution is called the antimedian, the points that maximizes the total distance from the facility to the users. Another solution is the anticenter, the points that maximizes the total distance from facilities to users. For more information about obnoxious facilities the reader is remitted to [5] -[7] . In the case of tree graphs, Ting [3] published a linear algorithm to find the antimedian of a tree, and Zelinka [4] proved that the set of leaves of a tree contains an antimedian. This problem can be approached through the axiomatization of location functions. The input of a location function consists of some information with respect to the users of the facilities, and the output is related to the consensus reached based on the given information. The rationality of this process is supported by the fact that location functions must satisfy a number of consensus axioms. The mean function on tree graphs was the first location function studied from the axiomatic point of view by Holzman [8] in the continuous case (in the continuous case a tree contains an infinity number of elements, the edges of the tree are considered to be rectifiable curves, and a profile 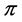 and its members are allowed to be located anywhere on edges). After that Vohra [9] also characterized the median function in the continuous case; in addition the reader can see [10] . In the discrete case, the center, the median, and the mean function have been characterized axiomatically on trees (see for example [11] -[20] ). Not much research has been done with respect to the axiomatic characterization of obnoxious location functions, but recently Balakrishnan et al. [21] published a characterization of the antimedian function on paths. In what follows, we present a different axiomatic characterization, also on paths, of the antimedian function. Ortega and Wang have recently sent for publication an axiomatic characterization of the antimean function on paths. For more information about location theory and axiomatization we refer the reader to the following references [22] -[27] .
and its members are allowed to be located anywhere on edges). After that Vohra [9] also characterized the median function in the continuous case; in addition the reader can see [10] . In the discrete case, the center, the median, and the mean function have been characterized axiomatically on trees (see for example [11] -[20] ). Not much research has been done with respect to the axiomatic characterization of obnoxious location functions, but recently Balakrishnan et al. [21] published a characterization of the antimedian function on paths. In what follows, we present a different axiomatic characterization, also on paths, of the antimedian function. Ortega and Wang have recently sent for publication an axiomatic characterization of the antimean function on paths. For more information about location theory and axiomatization we refer the reader to the following references [22] -[27] .
2. Preliminaries
Let 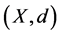 be a finite metric space and set
be a finite metric space and set

where 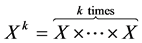 is the cartesian product of
is the cartesian product of![]() . The elements of
. The elements of ![]() are called
are called 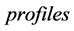 and usually denoted by
and usually denoted by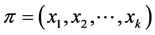 . Location theory and consensus theory are related to solve the following problem: Given a collection of
. Location theory and consensus theory are related to solve the following problem: Given a collection of 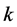 users (voters, customers, clients, etc.) with each user having a preferred location point in
users (voters, customers, clients, etc.) with each user having a preferred location point in![]() , one attempts to find a set of elements of
, one attempts to find a set of elements of ![]() that satisfy the preferences of the users with respect to some well-defined criteria. Modeling this situation requires the use of a location function on
that satisfy the preferences of the users with respect to some well-defined criteria. Modeling this situation requires the use of a location function on![]() , which is a function
, which is a function , where
, where ![]() denotes the set of all subsets of
denotes the set of all subsets of![]() . Three well known examples of location functions are:
. Three well known examples of location functions are:
a) the center function, denoted by Cen, and defined as
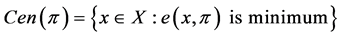
where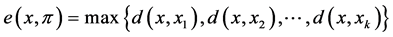 .
.
b) the median function, denoted by Med, and defined as

where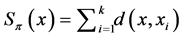 .
.
c) the mean function, denoted by Mean, and defined as
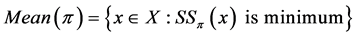
where .
.
We are interested in finite metric spaces defined in terms of connected graphs. Let  be a finite connected graph, and let
be a finite connected graph, and let 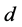 be the usual distance on
be the usual distance on![]() , where
, where 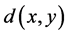 is the length of a shortest path between
is the length of a shortest path between  and
and![]() . It is well known that
. It is well known that 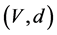 is a metric space, and observe that a profile in a graph
is a metric space, and observe that a profile in a graph ![]() is simply a sequence of vertices where repetitions are allowed. We will investigate some properties of the antimedian function on finite metric spaces defined in terms of a very special type of connected graphs, namely paths.
is simply a sequence of vertices where repetitions are allowed. We will investigate some properties of the antimedian function on finite metric spaces defined in terms of a very special type of connected graphs, namely paths.
3. The Antimedian Function on Paths
In this section ![]() or
or  will denote a path of length
will denote a path of length![]() . We will label the vertices of
. We will label the vertices of ![]() as
as ![]() and assume that the order that the vertices have in the path is given by the order of the numbers
and assume that the order that the vertices have in the path is given by the order of the numbers![]() . Hence,
. Hence, ![]() will be represented as
will be represented as
![]() (1)
(1)
Notice that the set of vertices is 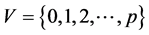 and also that vertex
and also that vertex ![]() is adjacent to vertex
is adjacent to vertex![]() , vertex
, vertex ![]() is adjacent to vertex
is adjacent to vertex ![]() and so on. In the case
and so on. In the case ![]() has an even number of vertices, we will write
has an even number of vertices, we will write . In the case
. In the case ![]() has an odd number of vertices, we will write
has an odd number of vertices, we will write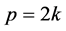 . Let
. Let  be a profile on
be a profile on![]() ; for any
; for any ![]() we define the status of
we define the status of 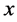 with respect to
with respect to 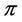 to be the number
to be the number

A vertex 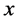 is called an antimedian of
is called an antimedian of 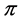 if
if
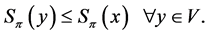
The antimedian of 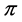 is the set
is the set
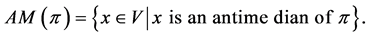
In order to study the antimedian function on![]() , we will divide the paths in two classes. The set of paths that have an odd number of vertices will be called odd paths, and the set of paths with an even number of vertices will be called even paths. Let
, we will divide the paths in two classes. The set of paths that have an odd number of vertices will be called odd paths, and the set of paths with an even number of vertices will be called even paths. Let 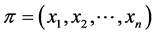 be a profile on
be a profile on![]() , the notation
, the notation
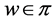
will indicate that there is 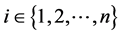 such that
such that . We also use
. We also use  to denote the set of all the different vertices included in
to denote the set of all the different vertices included in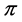 , and the number of vertices in the profile
, and the number of vertices in the profile 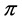 counting repetitions is denoted by
counting repetitions is denoted by![]() .
.
For example consider the profile 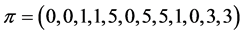 on
on ![]() with
with![]() . In this case
. In this case![]() ,
, 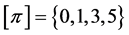 , and
, and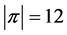 .
.
If 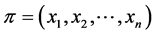 and
and  are profiles on
are profiles on![]() , denote by
, denote by ![]() the profile
the profile

The profile ![]() is called the concatenation of
is called the concatenation of 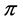 and
and![]() . The following result related to the antimedian function has been proved in [21] .
. The following result related to the antimedian function has been proved in [21] .
Lemma 1 Let  and
and 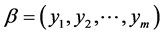 be profiles on
be profiles on![]() . If
. If , then
, then

The definition of the antimedian function implies the following characteristic of this function.
Lemma 2 Let 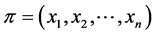 be a profile on
be a profile on![]() , and let
, and let ![]() be any permutation of
be any permutation of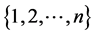 . Then
. Then

where 
The median function on finite tree graphs satisfies the following property that was proved in [13] , and will be important in the proof of several results.
Lemma 3 Let 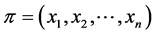 be a profile on a finite tree
be a profile on a finite tree![]() . If
. If 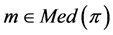 and if
and if  is a path contained in
is a path contained in ![]() such that
such that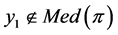 , then
, then
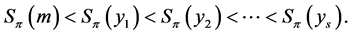
The property of the median function described by Lemma 3 will be called the increasing status property.
Lemma 4 Let 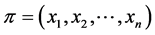 be a profile on a path
be a profile on a path ![]() of length
of length![]() . Then a)
. Then a) 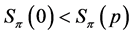 implies
implies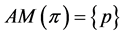 b)
b)  implies
implies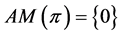 .
.
Proof. Notice first that a path is also a tree; consequently, we can apply to ![]() the increasing status property. We first obtain the set
the increasing status property. We first obtain the set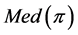 ; if
; if 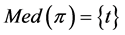 for some
for some![]() , then we define the paths
, then we define the paths
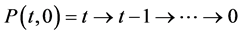
and
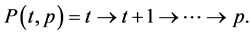
By the increasing status property we have
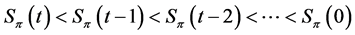
and

Observe that if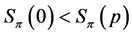 , then
, then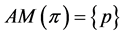 , and if
, and if , then
, then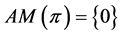 .
.
On the other hand, assume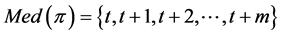 . Define the paths
. Define the paths

and
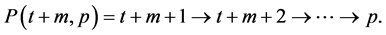
By the increasing status property we have
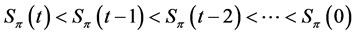
and
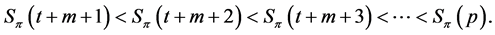
If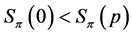 , then
, then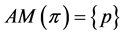 , and if
, and if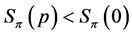 , then
, then .
. ![]()
We say that a profile 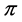 on
on ![]() is of the form
is of the form  for some integer
for some integer![]() , if
, if  contains exactly
contains exactly ![]() times the vertices
times the vertices ![]() and
and![]() . For example the profile
. For example the profile 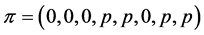 is of the form
is of the form . Profiles
. Profiles  of the form
of the form  are special for the antimedian functions because
are special for the antimedian functions because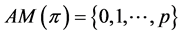 .
.
Lemma 5 Let  be a profile the form
be a profile the form 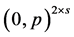 for some integer
for some integer ![]() on a path
on a path ![]() of length
of length![]() . Then
. Then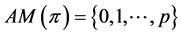 .
.
Proof. It is well known that if 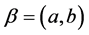 is a profile on a finite tree
is a profile on a finite tree![]() , the median of
, the median of 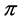 consists of all the vertices in the path
consists of all the vertices in the path

from  to
to . This implies that
. This implies that
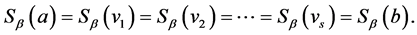
Since a path ![]() is also a tree, and if
is also a tree, and if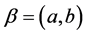 , then we have
, then we have
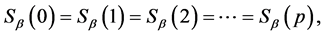
and the definition of the antimedian function implies that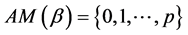 . Because
. Because  is of the form
is of the form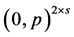 , then
, then , and we can reorder the vertices of
, and we can reorder the vertices of 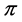 to define the profile
to define the profile

By Lemmas 1 and 2 we obtain
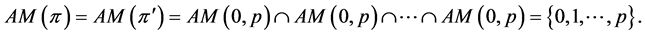
![]()
The next result characterizes profiles 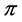 on a paths of length
on a paths of length ![]() that satisfy the condition
that satisfy the condition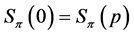 , and that are not of the form
, and that are not of the form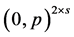 .
.
Lemma 6 Let ![]() be a path of length
be a path of length![]() , and let
, and let  be a profile that is not of the form
be a profile that is not of the form
 for some integer
for some integer![]() . If
. If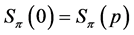 , then
, then .
.
Proof. Since ![]() is a tree we can apply the increasing status property. We start by obtaining the set
is a tree we can apply the increasing status property. We start by obtaining the set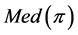 . If
. If 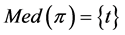 for some
for some![]() , then we define the paths
, then we define the paths
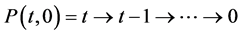
and
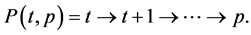
By the increasing status property we obtain

and

Observe that:
if , then
, then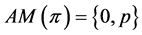 . On the other hand, assume
. On the other hand, assume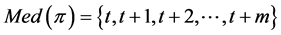 . Define the paths
. Define the paths

and

By the increasing status property we have

and
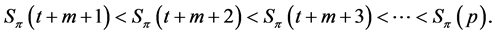
Note that 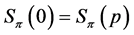 implies
implies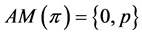 .
. ![]()
From Lemmas 4, 5, and 6 we obtain the following important result that characterizes the output of the antimedian function on paths of length![]() .
.
Lemma 7 If  is a profile on a path
is a profile on a path ![]() of length
of length![]() , then
, then

Assume
![]()
is a path of length![]() . If
. If 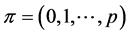 and
and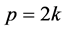 , then
, then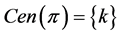 . Similarly, if
. Similarly, if  and
and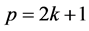 , then
, then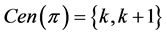 . Denote by
. Denote by 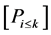 the set of vertices
the set of vertices ![]() such that
such that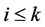 ; similarly we define the set
; similarly we define the set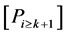 . Using the sets
. Using the sets

we define a partition of the profile 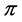 as follows: denote by
as follows: denote by 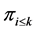 the profile such that
the profile such that 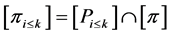 and each vertex in
and each vertex in 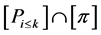 is included in the profile
is included in the profile 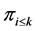 as many times it appears in
as many times it appears in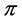 . In a similar way we define the profile
. In a similar way we define the profile  using the set
using the set . Notice that
. Notice that 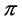 can be seen as the concatenation of profiles
can be seen as the concatenation of profiles 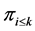 and
and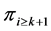 , in other words
, in other words . The following number
. The following number
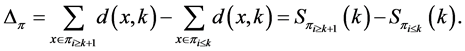 (2)
(2)
will play an important role in the following sections.
4. The Antimedian Function on Odd Paths
In this section
![]()
represents a path such that , and note that in this case
, and note that in this case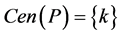 . Let
. Let  be a profile on
be a profile on![]() ; we will use
; we will use 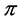 to define a new profile that will be denoted
to define a new profile that will be denoted . This profile contains the vertex
. This profile contains the vertex  repeated
repeated ![]() times. In other words we are assuming that
times. In other words we are assuming that 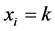 for all
for all![]() . So,
. So, 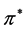 is the profile
is the profile
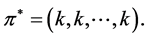
We want to establish a relationship between 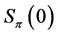 and
and . From the definition of profiles
. From the definition of profiles  and
and 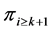 we derive the identities
we derive the identities
 (3)
(3)
and
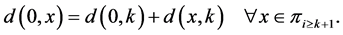 (4)
(4)
Using (3), (4), and the definitions of  and
and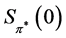 , we get
, we get
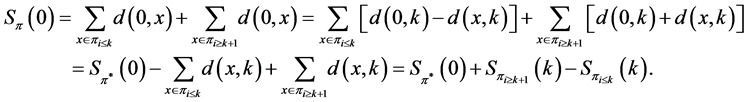
In terms of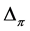 , defined by (2), and
, defined by (2), and 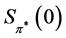 we deduce the following relation for
we deduce the following relation for 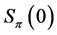
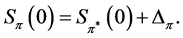
The next result is corollary to the definition of the number .
.
Corollary 1 If 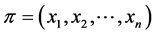 is a profile on
is a profile on![]() , then
, then 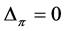 if and only if
if and only if .
.
The definition of 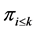 and
and 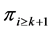 implies
implies
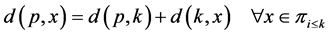

These relations imply
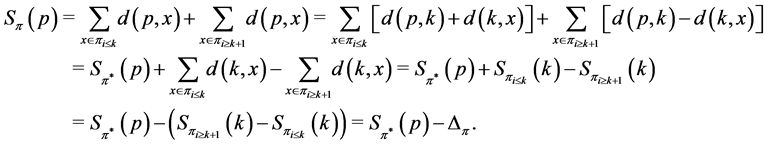
The definition of 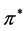 and the fact that
and the fact that 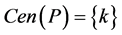 indicate
indicate
 (5)
(5)
The following three lemmas establish an important relationship between the numbers ,
, 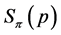 , and
, and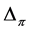 . These results will be used to characterize the antimedian of profiles
. These results will be used to characterize the antimedian of profiles 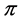 on
on![]() .
.
Lemma 8 If 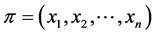 is a profile on
is a profile on![]() , then
, then 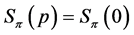 if and only if
if and only if .
.
Proof. Assume first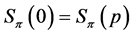 , and notice
, and notice
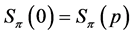
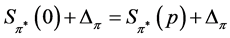

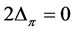
This implies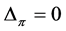 .
.
Because of (5) and the fact that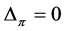 , we obtain
, we obtain

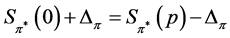
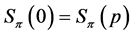
![]()
Replacing the equal sign with  and
and 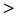 in the proof of Lemma 8, we obtain the next two results.
in the proof of Lemma 8, we obtain the next two results.
Lemma 9 If  is a profile on
is a profile on![]() , then
, then  if and only if
if and only if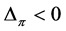 .
.
Lemma 10 If 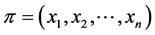 is a profile on
is a profile on![]() , then
, then  if and only if
if and only if .
.
We end this section with an important result that characterizes the antimedian of a profile  on odd paths that is not of the form
on odd paths that is not of the form 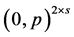 for some integer
for some integer![]() .
.
Lemma 11 Let 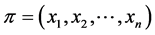 be a profile on an odd path
be a profile on an odd path![]() . If
. If 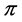 is not of the form
is not of the form  for some integer
for some integer![]() , then
, then

Proof. Assuming 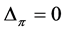 and because
and because  is not of the form
is not of the form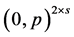 , then Lemma 8 implies
, then Lemma 8 implies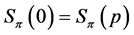 , and Lemma 6 proves
, and Lemma 6 proves .
.
If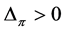 , then Lemma 10 shows
, then Lemma 10 shows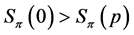 , and Lemma 4 demonstrates
, and Lemma 4 demonstrates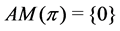 .
.
If , then Lemma 9 shows
, then Lemma 9 shows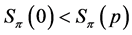 , and Lemma 4 proves
, and Lemma 4 proves .
. ![]()
5. The Antimedian Function on Even Paths
In this section
![]()
represents a path where ; so, we have
; so, we have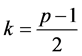 , and in this case
, and in this case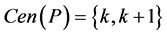 . Let
. Let 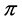 be a profile on
be a profile on![]() . Using similar ideas as in the last section, we can obtain a relationship between the numbers
. Using similar ideas as in the last section, we can obtain a relationship between the numbers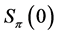 ,
, 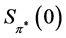 ,
, ![]() , and
, and . Since the profile
. Since the profile 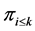 contains all the vertices of
contains all the vertices of 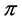 whose index is less or equal to
whose index is less or equal to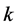 , then
, then
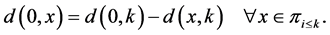 (6)
(6)
Using the profile  we obtain
we obtain
 (7)
(7)
From (6) and (7) and the definition of  and
and , we deduce
, we deduce

In terms of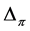 , we have the relation
, we have the relation
 (8)
(8)
Observe that

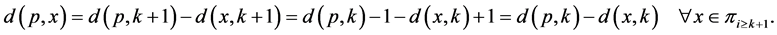
Using a similar argument as above, we obtain
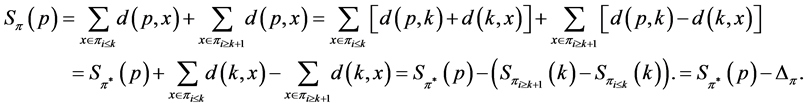
The definition of 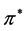 implies the identity
implies the identity
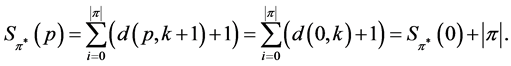
This identity provides the following relation between  and
and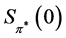 .
.
 (9)
(9)
The next three results show some properties of the numbers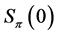 ,
,  ,
, ![]() , and
, and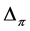 .
.
Lemma 12 If 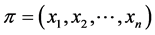 is a profile on
is a profile on , then
, then  if and only if
if and only if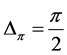 .
.
Proof. Assume first , and notice that (8) and (9) indicate
, and notice that (8) and (9) indicate
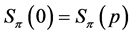

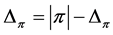
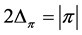

Conversely, if , then
, then
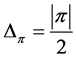
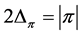
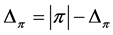
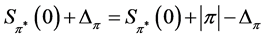
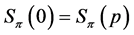
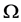
By replacing the equal sign with 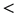 and
and  in the proof of Lemma 12, we obtain the following two results.
in the proof of Lemma 12, we obtain the following two results.
Lemma 13 If 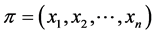 is a profile on
is a profile on , then
, then  if and only if
if and only if .
.
Lemma 14 If 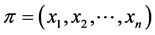 is a profile on
is a profile on , then
, then 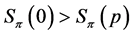 if and only if
if and only if .
.
The next lemma is an important result because it characterizes the antimedian of profiles , on even paths, that are not of the form
, on even paths, that are not of the form 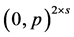 for some integer
for some integer![]() .
.
Lemma 15 Let  be a profile on an even path
be a profile on an even path . If
. If 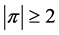 and
and 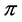 is not a profile of the form
is not a profile of the form 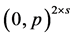 for some integer
for some integer![]() , then
, then
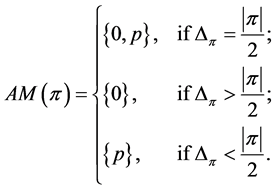
Proof. Assuming 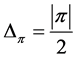 and since
and since 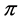 is not of the form
is not of the form , Lemma 12 shows
, Lemma 12 shows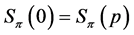 and Lemma 6 indicates
and Lemma 6 indicates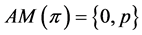 .
.
If , then Lemma 14 implies
, then Lemma 14 implies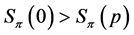 . Now Lemma 4 proves
. Now Lemma 4 proves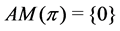 .
.
If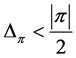 , then Lemma 13 shows
, then Lemma 13 shows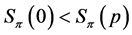 , and Lemma 4 implies
, and Lemma 4 implies .
. 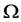
The next result is a corollary to Lemma 15.
Corollary 2 Let 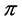 be a profile on
be a profile on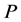 . If
. If  is of the form
is of the form 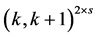 for some integer
for some integer![]() , then
, then 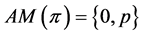 .
.
Proof. Notice that in this case the profile 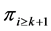 contains
contains ![]() times the vertex
times the vertex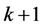 , and the profile
, and the profile 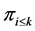 contains
contains ![]() times the vertex
times the vertex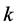 . Consequently, we have
. Consequently, we have

Finally, Lemma 15 implies .
. 
6. The Axioms and the Main Result
The axioms listed below are among the desirable properties that a general location function should satisfy, and it is not difficult to verify that the antimedian function satisfies these properties.
Oddness (O): Let  be a location function on a path
be a location function on a path 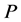 of length
of length ![]() with
with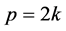 . Let
. Let  be defined as in (2); if
be defined as in (2); if 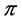 is not a profile of the form
is not a profile of the form 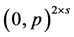 for some integer
for some integer![]() , then
, then

Evenness (E): Let 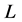 be a location function on a path
be a location function on a path 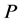 of length
of length ![]() with
with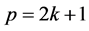 . Let
. Let 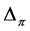 be defined as in (2); if
be defined as in (2); if  is not a profile of the form
is not a profile of the form 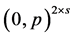 for some integer
for some integer![]() , then
, then
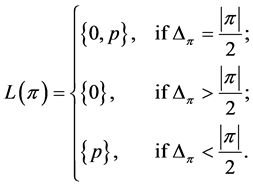
Consistency (C): Let 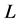 be a location function on
be a location function on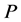 . If
. If  and
and 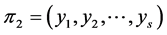 are profiles and
are profiles and 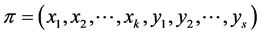 with
with , then
, then .
.
Extremeness (Ex): Let  be a location function, and
be a location function, and  be a profile on
be a profile on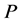 . If
. If , then
, then 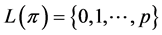 .
.
Generalized Extremeness (G-Ex): Let 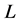 be a location function, and let
be a location function, and let 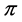 be a profile on
be a profile on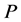 . If
. If 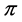 is of the form
is of the form 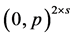 for some integer
for some integer![]() , then
, then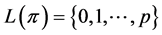 .
.
Anonymity (A): For any profile 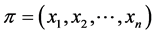 on
on  and any permutation
and any permutation 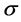 of
of , we have
, we have , where
, where 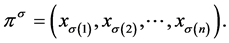
Some of these axioms are not independent. For example it is clear that (Ex) is a particular case of (G-Ex) when![]() . Next we prove that if a location function satisfies (C) and (Ex), it also satisfies (G-Ex).
. Next we prove that if a location function satisfies (C) and (Ex), it also satisfies (G-Ex).
Lemma 16 If 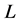 is a location function on
is a location function on  that satisfies axioms (C), (A), and (Ex), then
that satisfies axioms (C), (A), and (Ex), then  satisfies axiom (G-Ex).
satisfies axiom (G-Ex).
Proof. Let 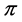 be a profile on
be a profile on  of the form
of the form 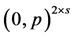 for some integer
for some integer![]() . Corollary 2 implies
. Corollary 2 implies 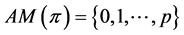 . Because of axiom (A), we can reorder the vertices of
. Because of axiom (A), we can reorder the vertices of 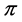 to obtain a profile
to obtain a profile 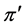 of the form
of the form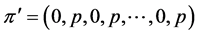 . We can express
. We can express 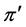 as a concatenation of profiles of the form
as a concatenation of profiles of the form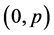 ; in other words
; in other words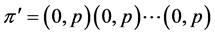 . Since
. Since 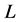 satisfies axiom (Ex), then
satisfies axiom (Ex), then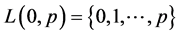 , and applying axiom (C) we conclude
, and applying axiom (C) we conclude


With the axioms listed above we will give two axiomatic characterizations for the antimedian function. The next theorem contains the first of these characterizations.
Theorem 1 Let 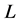 be a location function on
be a location function on .
. 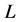 is the antimedian function on
is the antimedian function on 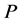 if and only if
if and only if 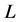 satisfies axioms (O), (E), (Ex), (C), and (A).
satisfies axioms (O), (E), (Ex), (C), and (A).
Proof. It is clear that if  is the antimedian function, then
is the antimedian function, then 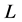 satisfies axioms (O), (E), (Ex), (C), and (A). Assume now
satisfies axioms (O), (E), (Ex), (C), and (A). Assume now 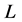 is a location function that satisfies axioms (O), (E), (Ex), (C), and (A). To prove that
is a location function that satisfies axioms (O), (E), (Ex), (C), and (A). To prove that 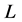 is the antimedian function we consider three cases.
is the antimedian function we consider three cases.
Case 1. Assume first 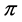 is a profile of the form
is a profile of the form 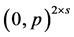 for some integer
for some integer![]() , by Lemma 5 we have
, by Lemma 5 we have . Since
. Since 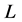 satisfies axioms (C), (A), and (Ex), then Lemma 16 proves
satisfies axioms (C), (A), and (Ex), then Lemma 16 proves 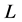 satisfies (G-Ex) which implies
satisfies (G-Ex) which implies . It is clear that in this case
. It is clear that in this case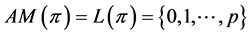 .
.
Case 2. Assume 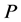 is a path such that
is a path such that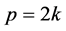 . Let
. Let  be a profile on
be a profile on 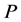 that is not of the form
that is not of the form 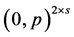 for some integer
for some integer![]() . Notice that
. Notice that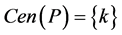 , and if
, and if , then Lemma 8 shows
, then Lemma 8 shows , and Lemma 6 implies
, and Lemma 6 implies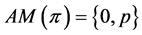 . On the other hand, since
. On the other hand, since  satisfies axiom (O) and
satisfies axiom (O) and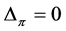 , then
, then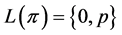 . Therefore,
. Therefore,  means
means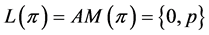 .
.
If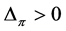 , then Lemma 10 indicates
, then Lemma 10 indicates , and Lemma 4 proves
, and Lemma 4 proves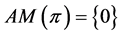 . Since
. Since 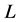 satisfies axiom (O) and
satisfies axiom (O) and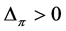 , we obtain
, we obtain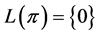 . From this we conclude that if
. From this we conclude that if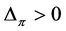 , then
, then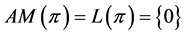 . A similar argument can be used to show that if
. A similar argument can be used to show that if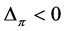 , then
, then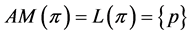 .
.
Case 3. Assume  is a path such that
is a path such that  which means
which means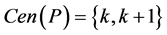 , and let
, and let 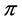 be a profile on
be a profile on 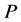 that is not of the form
that is not of the form 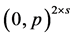 for some integer
for some integer![]() . If
. If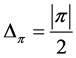 , then Lemma 12 demonstrates
, then Lemma 12 demonstrates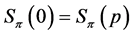 , and Lemma 6 proves
, and Lemma 6 proves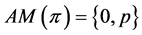 . Since
. Since 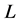 satisfies axiom (E) and
satisfies axiom (E) and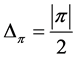 we get
we get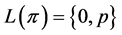 . Therefore,
. Therefore, 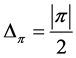 implies
implies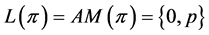 .
.
If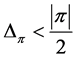 , then Lemma 13 indicates
, then Lemma 13 indicates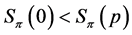 , and Lemma 4 shows
, and Lemma 4 shows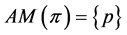 . Because
. Because 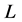 satisfies axiom (E) and
satisfies axiom (E) and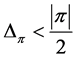 ,
, . Hence, when
. Hence, when 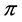 is a profile that is not of the form
is a profile that is not of the form  and
and ,
,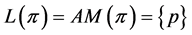 . A similar argument can be used to show that if
. A similar argument can be used to show that if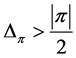 , then
, then
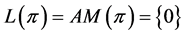 . Notice that Cases 1, 2, and 3 demonstrate the theorem.
. Notice that Cases 1, 2, and 3 demonstrate the theorem. 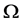
We leave it to the reader to prove that the axioms used in the proof of Theorem 1 are independent. Notice that in the proof of Theorem 1 we needed to use three axioms to establish Case 1. We want to improve the demonstration of this result using fewer axioms. We achieve this objective using axiom (G-Ex) in the following theorem which is our main result.
Theorem 2 Let 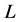 be a location function on
be a location function on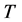 .
. 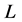 is the antimedian function on
is the antimedian function on 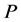 if and only if
if and only if  satisfies axioms (O), (E), and (G-Ex).
satisfies axioms (O), (E), and (G-Ex).
Proof. It is clear that if 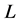 is the antimedian function, then
is the antimedian function, then  satisfies axioms (O), (E), and (G-Ex). Assume now that
satisfies axioms (O), (E), and (G-Ex). Assume now that  is a location function that satisfies axioms (O), (E), and (G-Ex). To prove that
is a location function that satisfies axioms (O), (E), and (G-Ex). To prove that  is the antimedian function we consider three cases.
is the antimedian function we consider three cases.
Case 1. Assume first 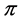 is a profile of the form
is a profile of the form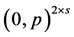 , then by Lemma 5 we obtain
, then by Lemma 5 we obtain  . Because
. Because 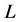 satisfies axiom (G-Ex), we have
satisfies axiom (G-Ex), we have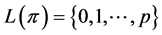 . So in this case
. So in this case .
.
Case 2. Assume  is a path such that
is a path such that 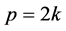 which means
which means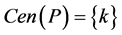 . Let
. Let 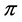 be a profile on
be a profile on  that is not of the form
that is not of the form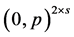 . If
. If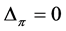 , then Lemma 8 indicates
, then Lemma 8 indicates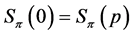 , and Lemma 6 implies
, and Lemma 6 implies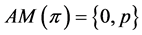 . Since
. Since 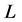 satisfies axiom (O) and
satisfies axiom (O) and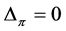 ,
,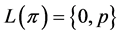 . Therefore,
. Therefore, 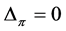 indicates
indicates . A similar argument can be employed to show that if
. A similar argument can be employed to show that if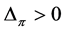 , then
, then 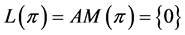 , and if
, and if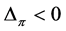 , then
, then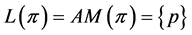 .
.
Case 3. Assume 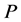 is a path such that
is a path such that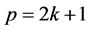 , and let
, and let 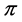 be a profile on
be a profile on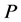 . Notice that
. Notice that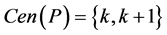 .
.
If , then Lemmas 12 implies
, then Lemmas 12 implies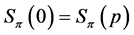 , and Lemma 6 shows
, and Lemma 6 shows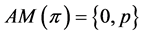 . Because
. Because 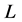 satisfies axiom (E), we conclude
satisfies axiom (E), we conclude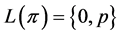 . Therefore,
. Therefore, 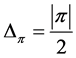 implies
implies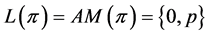 .
.
A similarly argument can be used to demonstrate that if , then
, then , and if
, and if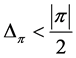 , then
, then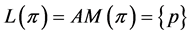 . It is clear that Cases 1, 2, and 3 finish the proof of the theorem.
. It is clear that Cases 1, 2, and 3 finish the proof of the theorem. 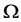
Notice that the definition of axioms (O), (E), and (G-Ex) indicate that they are independent. So it is not necessary to add a proof for the independence of these three axioms. More research is needed to find an axiomatic characterization of the antimedian function on tree graphs.
References
- Church, R.L. and Garinkel, R.S. (1978) Locating an Obnoxious Facility on a Network. Transportation Science, 12, 107-118. http://dx.doi.org/10.1287/trsc.12.2.107
- Minieka, E. (1983) Anti-Centers and Anti-Medians of a Network. Networks, 13, 359-365. http://dx.doi.org/10.1002/net.1027
- Ting, S.S. (1984) A Linear-Time Algorithm for Maxisum Facility Location on Tree Networks. Transportation Science, 18, 76-84. http://dx.doi.org/10.1287/trsc.18.1.76
- Zelinka, B. (1968) Medians and Peripherians of Trees. Archiv der Mathematik, 4, 87-95.
- Burkard, R.E., Dollani, H., Lin, Y. and Rote, G. (2001) The Obnoxious Center Problem on a Tree. SIAM Journal on Discrete Mathematics, 14, 498-509. http://dx.doi.org/10.1137/S0895480198340967
- Drezner, Z. and Wesolowsky, G.O. (1985) Location of Multiple Obnoxious Facilities. Transportation Science, 19, 193-202. http://dx.doi.org/10.1287/trsc.19.3.193
- Labbé, M. (1990) Location of an Obnoxious Facility on a Network: A Voting Approach. Networks, 20, 197-207. http://dx.doi.org/10.1002/net.3230200206
- Holzman, R. (1990) An Axiomatic Approach to Location on Networks. Mathematics of Operations Research, 15, 553-563.
- Vohra, R. (1996) An Axiomatic Characterization of Some Location in Trees. European Journal of Operational Research, 90, 78-84. http://dx.doi.org/10.1016/0377-2217(94)00330-0
- Foster, D.P. and Vohra, R. (1998) An Axiomatic Characterization of a Class of Location in Tree Networks. Operational Research, 46, 347-354. http://dx.doi.org/10.1287/opre.46.3.347
- Barthélemy, J.P. and McMorris, F.R. (1986) The Median Procedure for N-Trees. Journal of Classification, 3, 329-334. http://dx.doi.org/10.1007/BF01894194
- Barthélemy, J.P. and Monjardet, B. (1981) The Median Procedure in Cluster Analysis and Social Choice Theory. Mathematical Social Sciences, 1, 235-268. http://dx.doi.org/10.1016/0165-4896(81)90041-X
- Kriston, G. and Ortega, O. (2013) The Median Function on Trees. Discrete Mathematics, Algorithms and Applications, 4.
- McMorris, F.R., Mulder, H.M. and Ortega, O. (2010) Axiomatic Characterization of the Mean Function on Trees. Discrete Mathematics, Algorithms and Applications, 2, 313-329.
- McMorris, F.R., Mulder, H.M. and Ortega, O. (2012) The lp-Function on Trees. Networks, 60, 94-102.
- McMorris, F.R., Mulder, H.M. and Powers, R.C. (2003) The Median Function on Distributive Semilattices. Discrete Applied Mathematics, 127, 319-324. http://dx.doi.org/10.1016/S0166-218X(02)00213-5
- McMorris, F.R., Mulder, H.M. and Roberts, F.S. (1998) The Median Procedure on Median Graphs. Discrete Applied Mathematics, 84, 165-181. http://dx.doi.org/10.1016/S0166-218X(98)00003-1
- McMorris, F.R., Roberts, F.S. and Wang, C. (2001) The Center Function on Trees. Networks, 38, 84-87. http://dx.doi.org/10.1002/net.1027
- Mulder, H.M., Pelsmajer, M. and Reid, K.B. (2008) Axiomization of the Center Function on Trees. The Australasian Journal of Combinatorics, 41, 223-226.
- Ortega, O. (2008) Concensus and Location: The Mean Function. Ph.D. Disertation, Illinois Institute of Technology, Chicago.
- Balakrishnan, K., Changat, M., Mulder, H.H. and Subhamathi, A.R. (2012) Axiomatic Characterization of the Antimedian Function on Paths and Hypercubes. Discrete Mathematics, Algorithms and Applications, 4.
- Arrow, K.J., Sen, A.K. and Suzumura, K. (2002) Handbook of Social Choice and Welfare, Volumes 1, North Holland, Amsterdam.
- Arrow, K.J., Sen, A.K. and Suzumura, K. (2005) Handbook of Social Choice and Welfare, Volumes 2, North Holland, Amsterdam.
- Barthélemy, J.P. and Janowitz, M.F. (1991) A Formal Theory of Consensus. SIAM Journal on Discrete Mathematics, 4, 305-322. http://dx.doi.org/10.1137/0404028
- Day, W.H.E. and McMorris, F.R. (2003) Axiomatic Consensus Theory in Group Choice and Biomathematics. Frontiers in Applied Mathematics, SIAM, Philadelphia. http://dx.doi.org/10.1137/1.9780898717501
- Axiomatic Characterization of Loaction Functions. In: Kaul, H. and Mulder, H., Eds., Advances in Interdisciplinary Applied Discrete Mathematics, Interdisciplinary Mathematical Sciences, Vol. 11 (World Scientific Publishing, Singapure), 2010, 71-91.
- Mirchandani, P.B. and Francis, R.L. (1990) Discrete Location Theory. Wiley, New York.

