ABSTRACT

Let be a finite nilpotent group of odd order and be a subset of. We say that is complete if every element of can be represented as a sum of different elements of 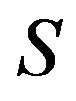and incomplete otherwise. In this paper, we obtain the characterization of large incomplete sets.

1. Introduction

Let be a finite additively written group (not necessarily commutative). Let be a subset of 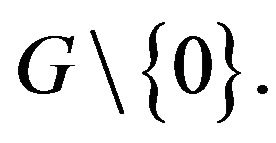Define { 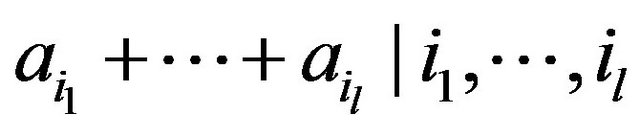are distinct }. For technical reasons we define We call an additive basis of if The critical number of is the smallest integer such that every subset of with 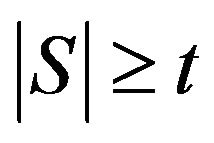forms an additive basis of 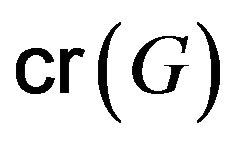was first introduced and studied by Erdős and Heilbronn in 1964 [1] for where is a prime. This parameter has been studied for a long time and its exact value is known for a large number of groups (see [2-10]).

Following Erdős [1], we say thatis complete ifand incomplete otherwise.

In this paper, we would like to study the following question: What is the structure of a relatively large incomplete set? Technically speaking, we would like to have a characterization for incomplete sets of relatively large size. Such a characterization has been obtained recently for finite abelian groups (see [11-13]). In this paper, we shall prove the following result.

Theorem 1.1. Let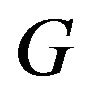be a finite nilpotent group with order where is the smallest prime dividing Also assume that is composite and Letbe a subset of such that If is incomplete, then there exist a subgroup of order and such that

2. Notations and Tools

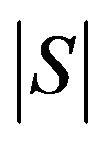If be a subset of the group, we shall denote by the cardinality of, by 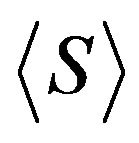the subgroup generated by. If are subsets of, let denote the set of all sums, where 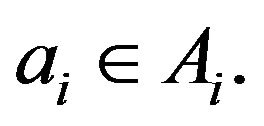Recall the following well known result obtained by Cauchy and Davenport.

Lemma 2.1. Let be a prime number. Let and be non-empty subsets of Then

We also use the following well known result.

Lemma 2.2 [14]. Let be a finite group. Let and be subsets of such that Then

Lemma 2.3 [3]. Let be a cyclic group of order, where are primes. Then

Lemma 2.4 [8]. Let be a non-abelian group of order where are distinct primes. Then

Lemma 2.5 [10]. Let be a finite nilpotent group of odd order and let be the smallest prime dividing If is a composite number then

Lemma 2.6. Let 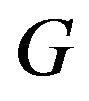be a finite nilpotent group of odd order and letbe the smallest prime dividing If then

Proof. Obviously, this follows from Lemmas 2.3-2.5.

Lemma 2.7 [15]. Let be a subset of a finite group of order. If then

Lemma 2.8 [16]. Let be a noncyclic group. Let be a subset Then

Let and As usual, we write We have the following result obtained by Olson.

Lemma 2.9 [5]. Letbe a nonempty subset of and Let Then

We shall also use the following result of Olson.

Lemma 2.10. Let be a finite group and letbe a generating subset of 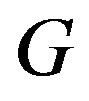such that Letbe a subset of such that Then there issuch that

This result follows by applying Lemma 3.1 of [15] to Let be a subset of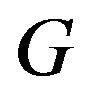with cardinality Let be an ordering of For set and

The ordering is called a resolving sequence of if, for each

The critical index of the resolving sequence is the largestsuch thatgenerates a proper subgroup of. Clearly, every nonempty subsetshas a resolving sequence.

We need the following basic property of resolving sequence which is implicit in [5].

Lemma 2.11. Letbe a generating subset of a finite groupsuch that

and

Let the orderingbe a resolving sequence ofwith critical index Then, there is a subset such that and

Proof. This is essentially formula (4) of [5]. By Lemma 2.9 we have

By Lemma 2.10 we have for each

On the other hand, by Lemma 2.8 we have

By the definition of, we have

By taking

we have the claimed inequality.

Lemma 2.12. Letbe a finite group with order where is the smallest prime dividing and Let be a subset of such that and 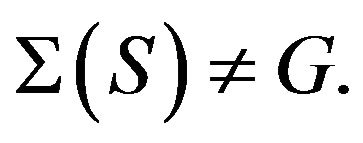Then there exists a set such that and

Proof. Since and is the smallest prime dividing we have By Lemma 2.7,

Clearly, we may partition such that and

We consider two cases.

Case 1.

Set. By Lemma 2.10, there issuch that

It follows by Lemma 2.9.

Since we have, by Lemma 2.2,

.

Case 2..

By Lemma 2.2,. Put. By Lemma 2.10, there is, such that

.

Therefore,

By Lemma 2.2,

implies

.

In both cases, one of the sets verifies the conclusion of the lemma. This completes the proof.

Lemma 2.13. Let, where is the smallest prime dividing If

and then

Proof. Set

and.

First, let us show that. Assume the contrary that We have

Since, we have

a contradiction to

Second, let us show that.

Assume the contrary. Since,

, we have 1)

On the other hand, since, we have

.

Then,

A contradiction to (1). Therefore, we have

This completes the proof.

Lemma 2.14. Letbe a finite group with order. Letbe a proper subgroup ofanda subset of If and 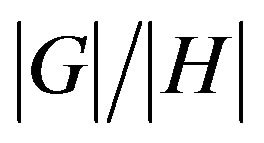is a primethen.

Moreover, if then there is

such that

Proof. By we shall mean, where is the canonical morphism. Put.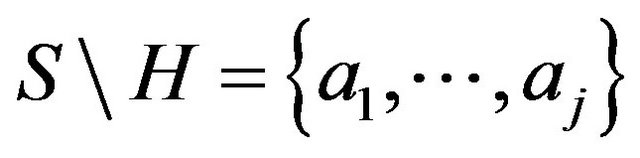

From our assumption we have

By Lemma 2.1, we have

It follows that

Assume now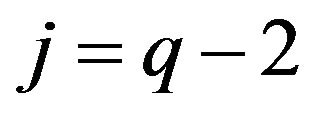. If there is such that say then

By Lemma 2.1, we have

a contradiction to Then there is such that

3. Proof of Theorem 1.1

Proof. By Lemma 2.12 there exists a set such that, and

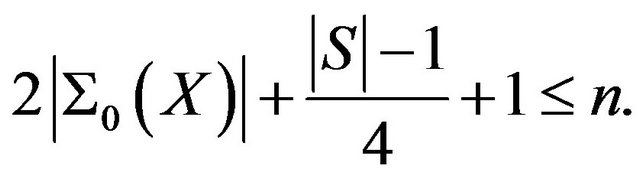(2)

We have

Therefore generates

By Lemma 2.11, there issuch thatverifying

(3)

Let be the subgroup generated byand letbe the smallest prime dividing.

Put Set

By (2) and (3), we have

By Lemma 2.13, we have

By Lemma 2.6, we get

Since 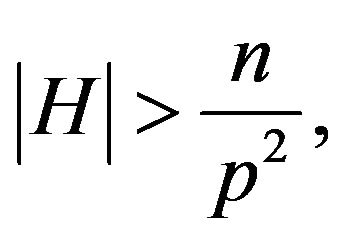we see easily that is a prime. Sinceis incomplete, we have

By Lemma 2.14,

We have

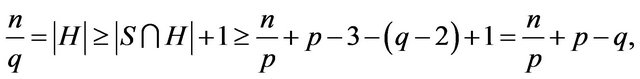
which impliesand Hence,

By Lemma 2.14, there exist a subgroupof orderand such that

4. Acknowledgements

The authors would like to thank the referee for his/her very useful suggestions. This work has been supported by the National Science Foundation of China with grant No. 11226279 and 11001035.

REFERENCES