Open Journal of Discrete Mathematics
Vol.3 No.3(2013), Article ID:34501,3 pages DOI:10.4236/ojdm.2013.33023
The Triangle Inequality and Its Applications in the Relative Metric Space*
1College of Mathematics and Information Science, Hebei Normal University, Shijiazhuang, China
2Department of Mathematics, Texas State University-San Marcos Texas State, San Marcos, USA
Email: suzj888@163.com, sipengli@126.com, js48@txstate.edu
Copyright © 2013 Zhanjun Su et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received January 10, 2013; revised April 20, 2013; accepted May 16, 2013
Keywords: Relative Distance; Triangle Inequality; Hexagon
ABSTRACT
Let C be a plane convex body. For arbitrary points
, denote by 
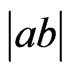the Euclidean length of the line-segment
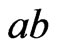. Let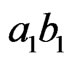 
be a longest chord of C parallel to the line-segment
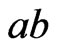. The relative distance 
between the points 
and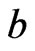 
is the ratio of the Euclidean distance between 
and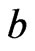 
to the half of the Euclidean distance between 
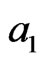and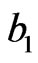
. In this note we prove the triangle inequality in 
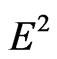with the relative metric
, and apply this inequality to show that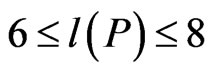
, where 
is the perimeter of the convex polygon 
measured in the metric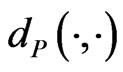
. In addition, we prove that every convex hexagon has two pairs of consecutive vertices with relative distances at least 1.
REFERENCES
- K. Doliwka and M. Lassak, “On Relatively Short and Long Sides of Convex Pentagons,” Geometriae Dedicata, Vol. 56, No. 2, 1995, pp. 221-224. doi:10.1007/BF01267645
- I. Fáry and E. Makai Jr., “Isoperimetry in Variable Metric,” Studia Scientiarum Mathematicarum Hungarica, Vol. 17, 1982, pp. 143-158.
- M. Lassak, “On Five Points in a Plane Body Pairwise in at Least Unit Relative Distances,” Colloquia Mathematica Societatis János Bolyai, Vol. 63, North-Holland, Amsterdam, 1994, pp. 245-247.
NOTES
*Su’s research was partially supported by National Natural Science Foundation of China (11071055) and NSF of Hebei Province (A2013- 205089).
Shen’s research was partially supported by NSF (CNS 0835834, DMS 1005206) and Texas Higher Education Coordinating Board (ARP 003615-0039-2007).