Open Journal of Discrete Mathematics
Vol.3 No.1(2013), Article ID:27368,3 pages DOI:10.4236/ojdm.2013.31004
Accelerated Series for Riemann Zeta Function at Odd Integer Arguments
1VTT Technical Research Centre of Finland, Espoo, Finland
2Department of Applied Physics, University of Eastern Finland, Kuopio, Finland
Email: juuso.olkkonen@vtt.fi, hannu.olkkonen@uef.fi
Received August 29, 2012; revised September 29, 2012; accepted October 12, 2012
Keywords: Riemann Zeta Function; Converging Series; Number Theory; Cryptography; Signal Processing; Compressive Sensing
ABSTRACT
Riemann zeta function is an important tool in signal analysis and number theory. Applications of the zeta function include e.g. the generation of irrational and prime numbers. In this work we present a new accelerated series for Riemann zeta function. As an application we describe the recursive algorithm for computation of the zeta function at odd integer arguments.
1. Introduction
The Riemann zeta function 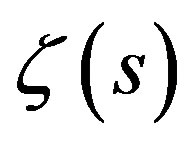 defined as for complex numbers s with
defined as for complex numbers s with 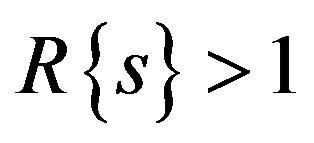
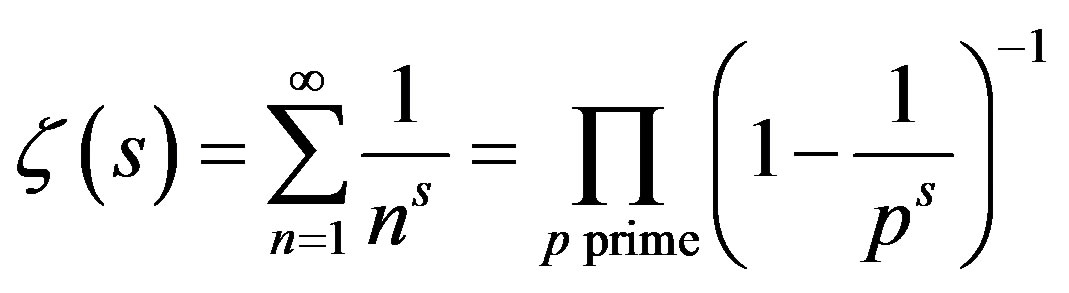 (1)
(1)
has a central role in number theory and appears in many areas of science and technology [1]. The Riemann zeta function is closely related to the prime numbers via (1) and it is an important tool in cryptography. Algorithms for evaluating 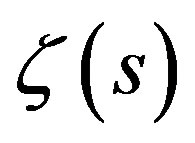 are vitally developing initialised by Euler, who invented the basic equation (1). Much of the research effort has been laid to the developing the accelerated series for computation of
are vitally developing initialised by Euler, who invented the basic equation (1). Much of the research effort has been laid to the developing the accelerated series for computation of  for integer arguments [1-4]. For even s, the Riemann zeta function obeys the general rule
for integer arguments [1-4]. For even s, the Riemann zeta function obeys the general rule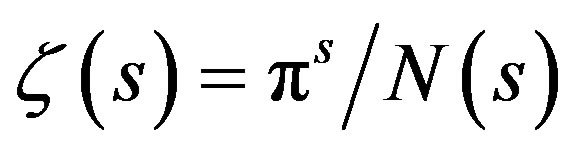 , where
, where  is an integer. For odd s, no closed form solution for
is an integer. For odd s, no closed form solution for 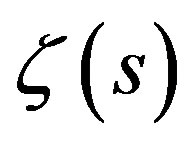 has been solved and the computational algorithms are usually based on the acceleration of the series (1) by asymptotic expansion with Bernoulli numbers or via Euler's transformation [2]. Recursive algorithms have also presented for evaluation of
has been solved and the computational algorithms are usually based on the acceleration of the series (1) by asymptotic expansion with Bernoulli numbers or via Euler's transformation [2]. Recursive algorithms have also presented for evaluation of 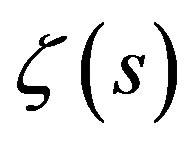 at odd integers [5].
at odd integers [5].
In this work we describe a new accelerated series for the Riemann zeta function at integer arguments. The main result is involved in Theorem 1.
Theorem 1: Let us suppose that 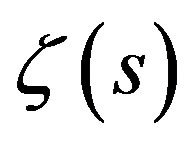 is the Riemann zeta function defined by (1). The following series converges as
is the Riemann zeta function defined by (1). The following series converges as
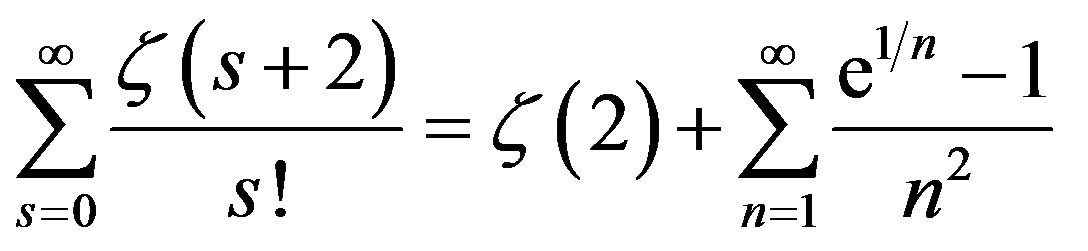
In Section 2 we give the proof of Theorem 1. In Section 3 we present derivatives of Theorem 1 and describe the method for accelerating the zeta function series given by Theorem 1. In Section 4 we describe the recursive algorithm for evaluation of the Riemann zeta function at integer arguments.
2. Proof of Theorem 1
We may deduce
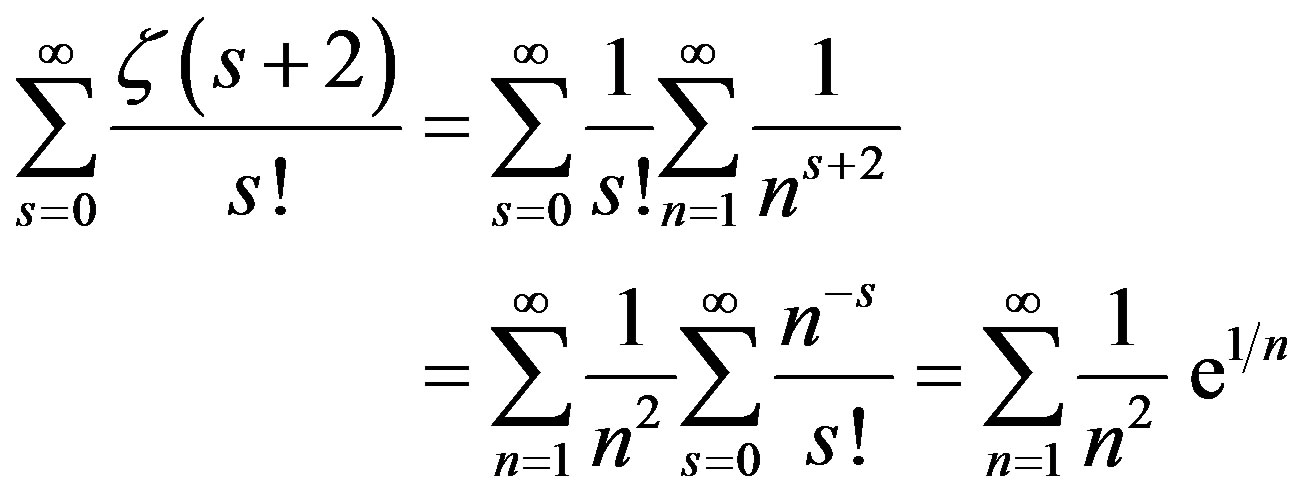 (2)
(2)
The series (2) converges very slowly. However, we may write
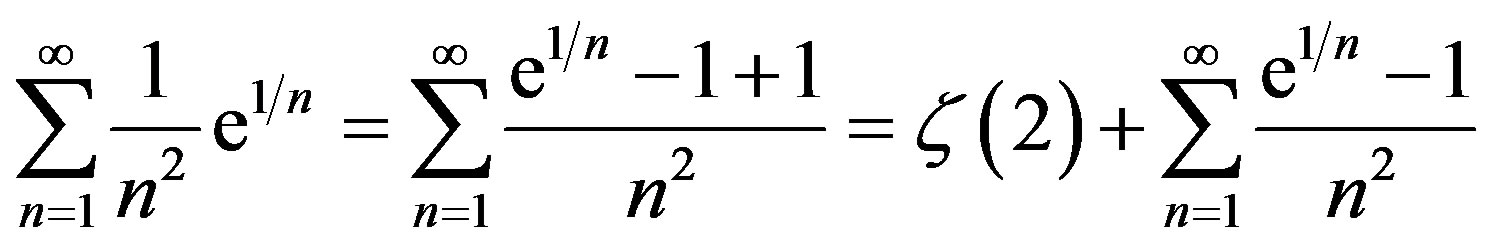 (3)
(3)
which has an accelerated convergence. The proof is now completed.
3. Derivatives of Theorem 1
Lemma 1: For 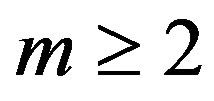
 (4)
(4)
Proof: Similar as Theorem 1.
Lemma 2: For 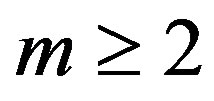
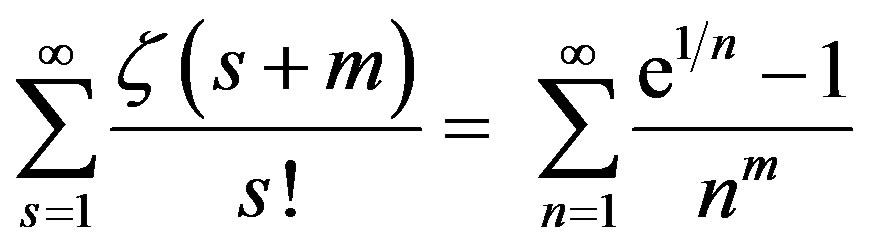 (5)
(5)
Proof: Follows directly from Lemma 1 by elimination of the first term in series (4).
Lemma 3:
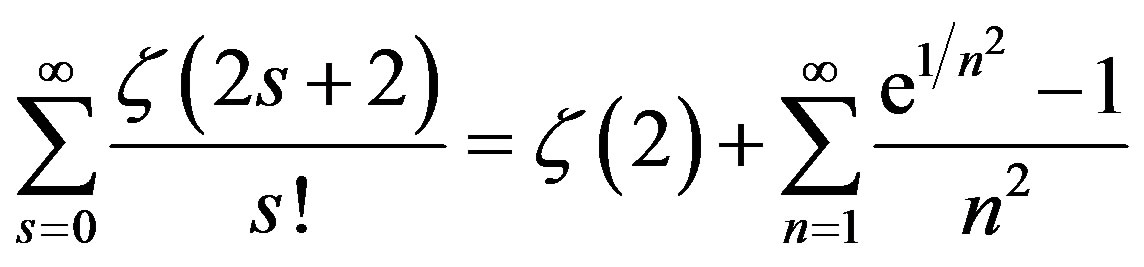 (6)
(6)
Proof: Similar as Theorem 1.
Lemma 4:
 (7)
(7)
Proof: Follows directly Lemma 3.
Lemmas 3 and 4 can be generalised as Lemma 5: For 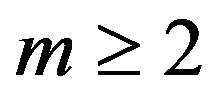
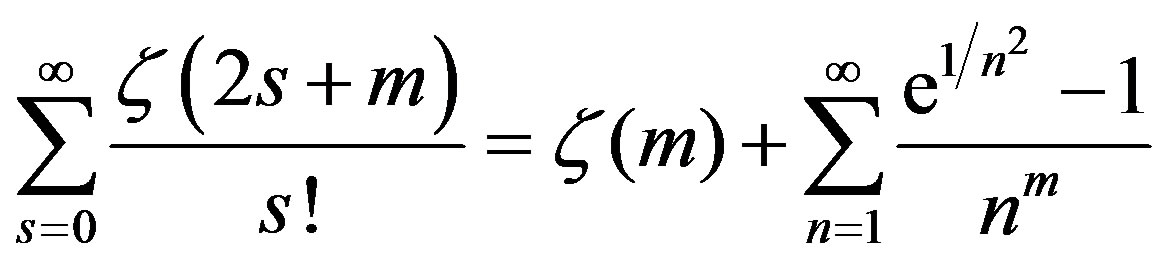 (8)
(8)
Lemma 6: For 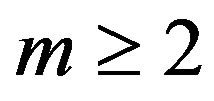
 (9)
(9)
The last series (Lemma 6) can be further generalized as Lemma 7: For 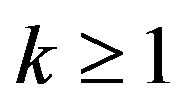 and
and 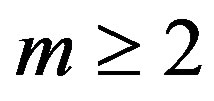
 (10)
(10)
The series can be further accelerated by noting that . We may write Lemma 7 as
. We may write Lemma 7 as

which gives Lemma 8: For  and
and 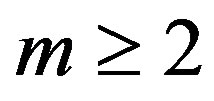
 . (11)
. (11)
4. Recursive Algorithm
From Lemma 8 we may deduce Lemma 9: For  and
and 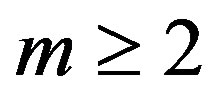
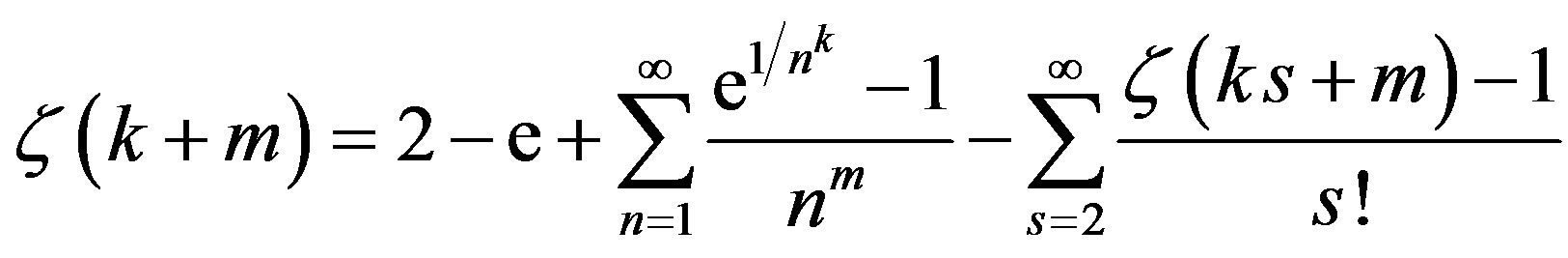 (12)
(12)
The last series can be computed if ,
,  are known. This leads to the fast recursive computation of the zeta function. Especially for
are known. This leads to the fast recursive computation of the zeta function. Especially for 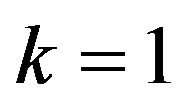 we obtain the sequential
we obtain the sequential 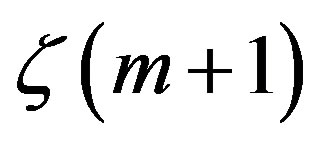 values as
values as
 (13)
(13)
Both series in (13) have accelerated convergence and to obtain the required accuracy only a few previously computed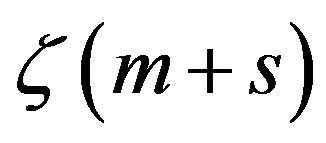 ,
, 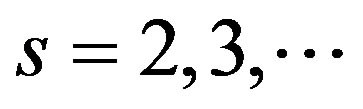 values are needed.
values are needed.
5. Discussion
In this work we present a new accelerated series for Riemann zeta function. The key observation is presented in Theorem 1. The infinite summation of the zeta functions weighted by 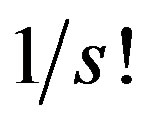 can be represented by fast converging series. One application is the recursive computation of the zeta function from the sequence of previously known zeta function values. The recursive algorithm can be initialised using (13), which has itself accelerated convergence. Especially in high values of
can be represented by fast converging series. One application is the recursive computation of the zeta function from the sequence of previously known zeta function values. The recursive algorithm can be initialised using (13), which has itself accelerated convergence. Especially in high values of 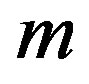 the first series in (13) has high convergence due to the term
the first series in (13) has high convergence due to the term 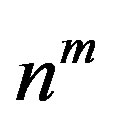 in the denominator.
in the denominator.
The zeta function values for odd integers are generally believed to be irrational, thought consistent proof is given only for 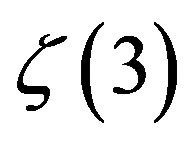 [6,7]. The irrational number sequences, which can be easily reproduced from a few parameters are important e.g. in encryption coding. The recursive algorithm (Lemma 9) serves as a good candidate for the irrational number generator, since it requires only two parameters
[6,7]. The irrational number sequences, which can be easily reproduced from a few parameters are important e.g. in encryption coding. The recursive algorithm (Lemma 9) serves as a good candidate for the irrational number generator, since it requires only two parameters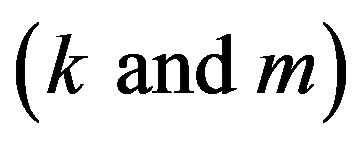 . By altering the parameters a countless number of irrational number sequences are obtained.
. By altering the parameters a countless number of irrational number sequences are obtained.
Recently a close connection with the log-time sampled signals and the zeta function has been observed [8]. The zeta transform allows the analysis and synthesis of the log-time sampled signals for example in compressive sensing applications.
6. Acknowledgements
This work was supported by the National Technology Agency of Finland (TEKES). The authors would like to thank the anonymous reviewers for their valuable comments.
REFERENCES
- J. M. Borwein, D. M. Bradley and R. E. Crandall, “Computational Strategies for the Riemann Zeta Function,” Journal of Computational and Applied Mathematics, Vol. 121, No. 1-2, 2000, pp. 247-296. doi:10.1016/S0377-0427(00)00336-8
- E. Grosswald, “Remarks Concerning the Values of the Riemann Zeta Function at Integral, Odd Arguments,” Journal of Number Theory, Vol. 4, No. 3, 1972, pp. 225- 235. doi:10.1016/0022-314X(72)90049-2
- D. Cvijović and J. Klinowski, “Integral Representations of the Riemann Zeta Function for Odd-Integer Arguments,” Journal of Computational and Applied Mathematics, Vol. 142, No. 2, 2002, pp. 435-439. doi:10.1016/S0377-0427(02)00358-8
- T. Ito, “On an Integral Representation of Special Values of the Zeta Function at Odd Integers,” Journal of Mathematical Society of Japan, Vol. 58, No. 3, 2006, pp. 681- 691. doi:10.2969/jmsj/1156342033
- H. Olkkonen and J. T. Olkkonen, “Fast Converging Series for Riemann Zeta Function,” Open Journal of Discrete Mathematics, Vol. 2, No. 4, 2012, pp. 131-133. doi:10.4236/ojdm.2012.24025
- R. Apéry, “Irrationalité de ζ(2) et ζ(3),” Astérisque, Vol. 61, 1979, pp. 11-13.
- F. Beukers, “A Note on the Irrationality of ζ(2) and ζ(3),” Bulletin London Mathematical Society, Vol. 11, No. 3, 1979, pp. 268-272. doi:10.1112/blms/11.3.268
- H. Olkkonen and J. T. Olkkonen, “Log-Time Sampling of Signals: Zeta Transform,” Open Journal of Discrete Mathematics, Vol. 1, No. 2, 2011, pp. 62-65. doi:10.4236/ojdm.2011.12008

