Open Journal of Discrete Mathematics
Vol.1 No.1(2011), Article ID:4582,3 pages DOI:10.4236/ojdm.2011.11004
Greedy Friensdhip Decompositions of Graphs*
Departamento de Matem_atica, FCT-UNL and CMA-UNL, Quinta da Torre, Caparica, Portugal
E-mail: tmjs@fct.unl.pt
Received March 13, 2011; revised March 20, 2011; accepted April 2, 2011
Keywords: friendship graph, decompositions, greedy decompositions
Abstract
A graph that consists of t cliques sharing a vertex v is said to be a t-friendship graph with center v. A friendship graph is a graph that is t-friendship for some![]() . We solve the problem of finding the best upper bound for the size of a greedy 2-friendship decomposition and a greedy friendship decomposition of graphs of order n.
. We solve the problem of finding the best upper bound for the size of a greedy 2-friendship decomposition and a greedy friendship decomposition of graphs of order n.
1. Introduction
For notation and terminology not discussed here the reader is referred to [2]. All graphs considered here are finite and simple, i.e., they have no loops or multiple edges. Let G be a simple graph with vertex set 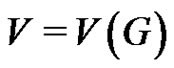 and edge set
and edge set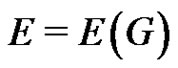 . The degree of a vertex
. The degree of a vertex 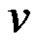 will be denoted by
will be denoted by 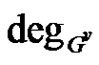 or briefly by
or briefly by 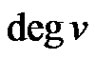 if it is clear which graph is being considered. A clique is a complete graph and the complete bipartite graph with parts of size m and n will be denoted by
if it is clear which graph is being considered. A clique is a complete graph and the complete bipartite graph with parts of size m and n will be denoted by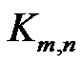 . A graph that consists of t cliques sharing a vertex v is said to be a t-friendship graph (t-fs graph) with center v. A friendship graph is a graph that is t-friendship for some
. A graph that consists of t cliques sharing a vertex v is said to be a t-friendship graph (t-fs graph) with center v. A friendship graph is a graph that is t-friendship for some![]() . A (t-)friendship decomposition of a graph G is a set of pairwise edge disjoint (t-)friendship subgraphs of G, such that every edge of G appears in exactly one element of the decomposition. Let
. A (t-)friendship decomposition of a graph G is a set of pairwise edge disjoint (t-)friendship subgraphs of G, such that every edge of G appears in exactly one element of the decomposition. Let 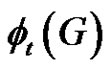 be the minimum number of elements in a t-friendship decomposition of G. The main goal is to study the function
be the minimum number of elements in a t-friendship decomposition of G. The main goal is to study the function
![]()
which is the smallest number such that any graph G of order n admits a t-friendship decomposition with at most 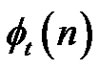 elements.
elements.
Observe that a 1-friendship graph is just a clique. Erdös, Goodman and Pósa [3] proved that 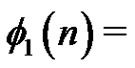
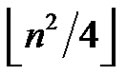 . Sousa [5] determined the exact value of the function
. Sousa [5] determined the exact value of the function 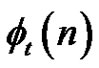 for
for 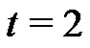 and
and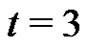 , and for
, and for 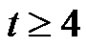 its asymptotic value, as n tends to infinity, was determined. More precisely, Sousa [5] proved that
its asymptotic value, as n tends to infinity, was determined. More precisely, Sousa [5] proved that 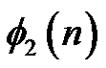 equals
equals 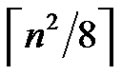 if n is even and
if n is even and 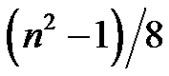 if n is odd; and that
if n is odd; and that 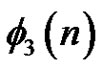 equals
equals 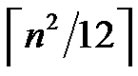 if n is even and
if n is even and 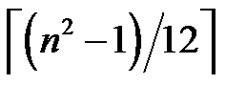 if n is odd and not equal to 5. For
if n is odd and not equal to 5. For 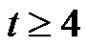 it was proved that
it was proved that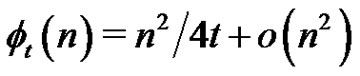 .
.
In this paper our aim is to study the problem of looking not at an optimal friendship decomposition of graphs but at greedy friendship decompositions of graphs. The motivation for this work comes from the work or McGuinness [4] about clique decompositions of graphs, proving a conjecture of Winkler [1]. (Note that a clique is simple a 1-friendship graph.) McGuinness proved that if maximal cliques are removed one by one from any graph with n vertices, then the graph will be empty after at most 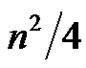 steps. He also proves that this in fact best possible. The result is the following.
steps. He also proves that this in fact best possible. The result is the following.
Theorem 1 [4] Any greedy clique decomposition of a graph with n vertices has at most 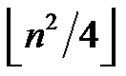 cliques, and it has exactly
cliques, and it has exactly 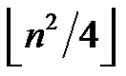 cliques if and only if the graph is
cliques if and only if the graph is
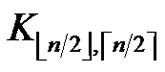 .
.
Note that the result of McGuinness is strong in the sense that for clique decompositions of graphs the optimal values are the same whether you consider optimal clique decompositions or greedy clique decompositions. With this work our goal is to see what happens if instead of 2-friendship decompositions of graphs one considers greedy 2-friendship decompositions of graphs. We will see later that the best values are not the same, in fact, they are quite far apart.
We start our work by properly defining the notion of a maximal (t-)friendship subgraph of a graph. A (t-)friendship subgraph of a graph G is said to be maximal if it is not a proper subgraph of another (t-)friendship subgraph of G and its cliques can be ordered in such a way that each clique is maximal in the graph obtained after the edge set of the previous cliques have been removed. A greedy (t-)friendship decomposition of G is formed by choosing a maximal (t-)friendship graph in G, then choosing a maximal (t-)friendship graph in the graph remaining after deleting the edges of the first (t-)friendship graph and continuing removing maximal (t-)friendship graphs until the graph is empty. We will always assume that the elements of the decomposition are chosen in a certain order.
For greedy 2-friendship decompositions we will prove that any greedy 2-friendship decomposition of a graph of order n has at most 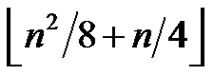 elements. Furthermore, for
elements. Furthermore, for 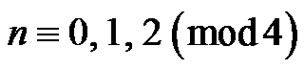 a greedy 2-friendship decomposition of a graph of order n can have exactly
a greedy 2-friendship decomposition of a graph of order n can have exactly 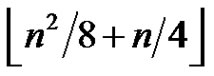 elements if and only if the graph is
elements if and only if the graph is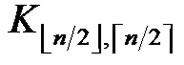 . For
. For 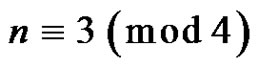 a greedy 2-friendship decomposition of
a greedy 2-friendship decomposition of 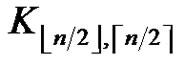 can have exactly
can have exactly 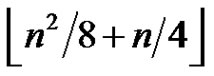 2-friendship graphs, however, in this case we can also have equality for non-bipartite graphs. We conclude by showing that any greedy friendship decomposition of a graph of order n has at most
2-friendship graphs, however, in this case we can also have equality for non-bipartite graphs. We conclude by showing that any greedy friendship decomposition of a graph of order n has at most 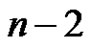 elements and we also prove that this upper bound is, in fact, best possible.
elements and we also prove that this upper bound is, in fact, best possible.
2. Greedy Friendship Decompositions
We start this section with the following result about greedy 2-friendship decompositions of graphs and conclude with a result concerning greedy friendship decompositions of graphs.
Theorem 1 Any greedy 2-friendship decomposition of a graph of order n has at most 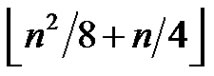 2-friendship graphs.
2-friendship graphs.
Proof. Let G be a graph with n vertices, where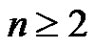 , and
, and 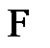 a greedy 2-fs decomposition of G. Using the same order in which the elements of
a greedy 2-fs decomposition of G. Using the same order in which the elements of 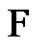 were chosen we construct a greedy clique decomposition of G,
were chosen we construct a greedy clique decomposition of G, ![]() , as follows:
, as follows:
Let 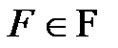 and let
and let 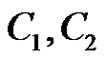 be its cliques. Assume without loss of generality that
be its cliques. Assume without loss of generality that 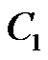 is maximal, then we first add
is maximal, then we first add 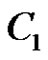 to
to ![]() and then add
and then add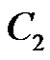 .
.
Clearly ![]() is a greedy clique decomposition of G. Let
is a greedy clique decomposition of G. Let 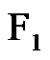 be the set of all 2-fs graphs in
be the set of all 2-fs graphs in 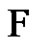 that have exactly 1 clique and
that have exactly 1 clique and 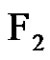 the set of all 2-fs graphs in
the set of all 2-fs graphs in 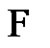 that have exactly 2 cliques. Then,
that have exactly 2 cliques. Then,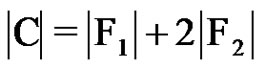 . Observe that
. Observe that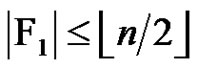 . Therefore,
. Therefore,
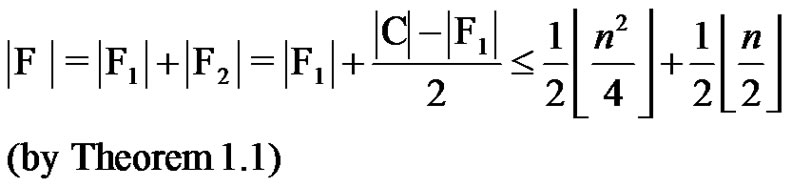 (2.1)
(2.1)
Easy calculations show that 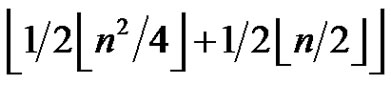
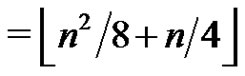 and the result follows.
and the result follows. 
Theorem 2 Let 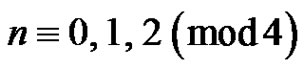 and let G be a graph of order n. Then G admits a greedy 2-friendship decomposition with exactly
and let G be a graph of order n. Then G admits a greedy 2-friendship decomposition with exactly 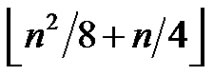 elements if and only if
elements if and only if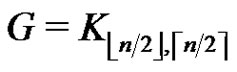 .
.
Proof. Let 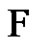 be a greedy 2-friendship decomposition of the graph G with exactly
be a greedy 2-friendship decomposition of the graph G with exactly 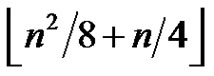 elements. Let
elements. Let ![]() and
and 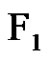 be as in the proof of Theorem 2.1. Suppose that
be as in the proof of Theorem 2.1. Suppose that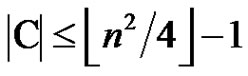 . From (2.1) we obtain
. From (2.1) we obtain
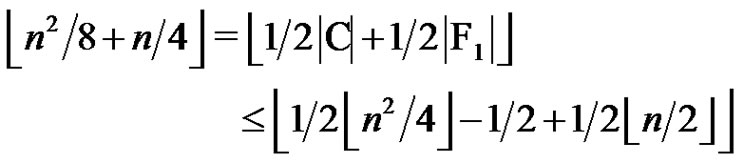
which is a contradiction for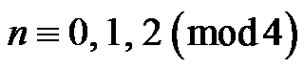 . Therefore
. Therefore 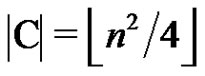 and Theorem 1 implies that
and Theorem 1 implies that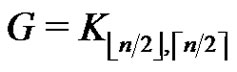 .
.
Now assume that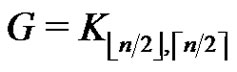 . It suffices to find a 2-fs decomposition of G, say
. It suffices to find a 2-fs decomposition of G, say , with exactly
, with exactly 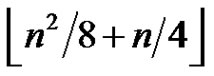 elements. Let A, B be a partition of G with
elements. Let A, B be a partition of G with 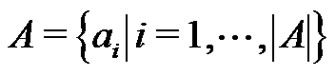 and
and 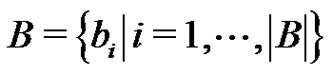 and assume, without loss of generality, that
and assume, without loss of generality, that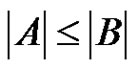 . We consider three different cases.
. We consider three different cases.
a) Assume that 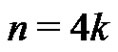 and construct
and construct  as follows:
as follows:
i) For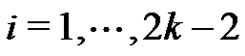 , pair all the edges incident with
, pair all the edges incident with 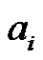 except the edges
except the edges 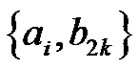 and
and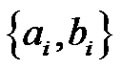 , and for
, and for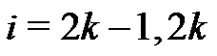 , pair all the edges incident with
, pair all the edges incident with 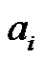 except the edges
except the edges 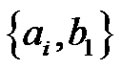 and
and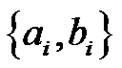 . In total
. In total 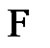 will get
will get 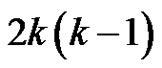 elements.
elements.
ii) Observe that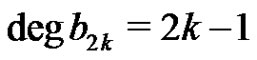 , so we pair all the edges incident with
, so we pair all the edges incident with 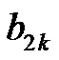 except the edge
except the edge 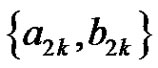 to get
to get 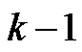 2-fs graphs and we consider the 2-fs graph with edges
2-fs graphs and we consider the 2-fs graph with edges 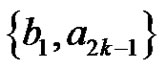 and
and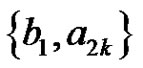 . In total
. In total 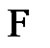 will increase by k elements.
will increase by k elements.
iii) At this step the 2k edges left form a perfect matching and we add them all to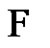 .
.
Thus,
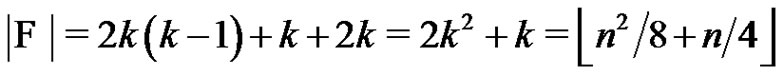
b) Assume that 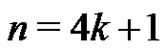 and construct
and construct 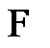 as follows:
as follows:
i) For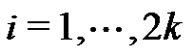 , pair all the edges incident with
, pair all the edges incident with 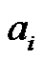 except edges
except edges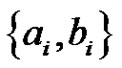 . In total
. In total 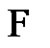 will get
will get 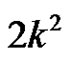 elements.
elements.
ii) At this step the 2k edges left form a matching and we add them all to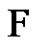 .
.
Therefore,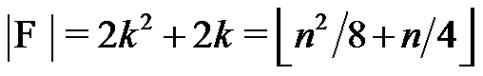 .
.
c) Assume that 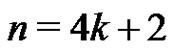 and construct
and construct  as follows:
as follows:
i) For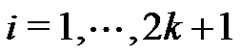 , pair all the edges incident with
, pair all the edges incident with 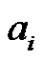 except edges
except edges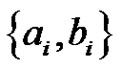 . In total
. In total  will get
will get 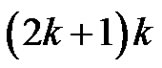 elements.
elements.
ii) For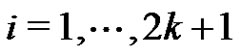 , pair all the edges incident with
, pair all the edges incident with 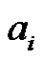 except edges
except edges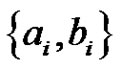 . In total
. In total 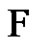 will get
will get 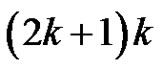 elements.
elements.
Therefore,
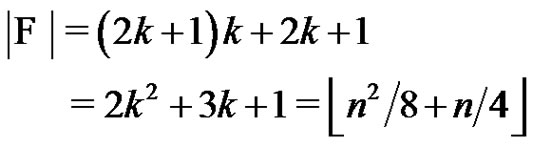 .
.
Remark: The following example shows that for 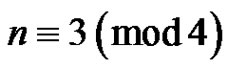
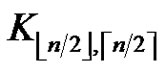 is not the only extremal graph for greedy 2-friendship decompositions.
is not the only extremal graph for greedy 2-friendship decompositions.
Example: Let 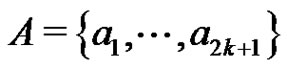 and
and 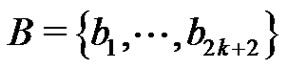 and let G be the complete bipartite graph with parts A and B plus the edge
and let G be the complete bipartite graph with parts A and B plus the edge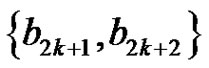 . Construct
. Construct 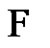 as follows:
as follows:
i) For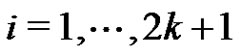 , pair all the edges incident with
, pair all the edges incident with ![]() except edges
except edges 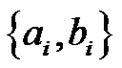 and the edge
and the edge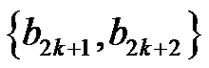 . In total
. In total 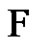 will get
will get 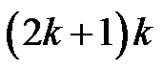 elements.
elements.
ii) Pair all the edges incident with 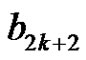 except the edges
except the edges 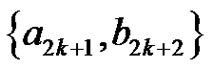 and
and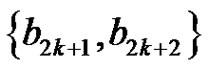 , then
, then 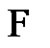 will increase by k elements.
will increase by k elements.
iii) Finally, we add to 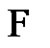 the single edges
the single edges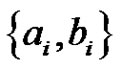 , for
, for 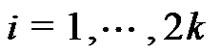 and the 2-fs graph with edges
and the 2-fs graph with edges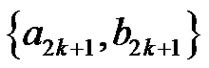 ,
, 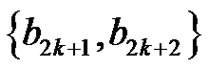 and
and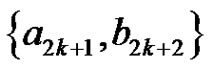 , thus we add
, thus we add 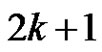 elements to
elements to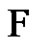 .
.
Therefore,
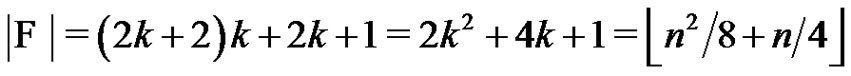
and the graph G is not bipartite.
We conclude this section with the following trivial theorem on the size of a greedy friendship decomposition of a graph.
Theorem 3 Any greedy friendship decomposition of a graph of order n, where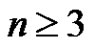 , has at most
, has at most 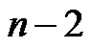 elements. Furthermore, this bound is sharp for the bipartite graph
elements. Furthermore, this bound is sharp for the bipartite graph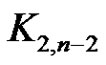 .
.
Proof. Let G be a graph with 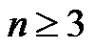 vertices. We will proceed by induction on n. If
vertices. We will proceed by induction on n. If 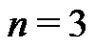 then the edges of G form either a triangle or path of length 1 or 2, thus any friendship decomposition of G will have exactly one element. Suppose the result holds for graphs with less than n vertices. Let
then the edges of G form either a triangle or path of length 1 or 2, thus any friendship decomposition of G will have exactly one element. Suppose the result holds for graphs with less than n vertices. Let 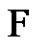 be a greedy friendship decomposition G, let F be the first friendship graph picked for
be a greedy friendship decomposition G, let F be the first friendship graph picked for 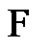 and let v be its center. Consider the graph H with vertex set
and let v be its center. Consider the graph H with vertex set 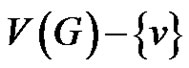 and
and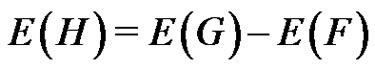 . Clearly
. Clearly 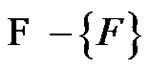 is a greedy friendship decomposition of H, so by induction
is a greedy friendship decomposition of H, so by induction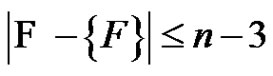 , hence the result.
, hence the result. 
3. References
[1] J. Bang-Jensen and B. Toft. Unsolved problems presented at the Julius Petersen Graph Theory Conference. Discrete Math., 101(1-3): 351-360, 1992. doi:10.1016/0012-365X(92)90616-N
[2] R. Diestel. Graph Theory. Springer-Verlag, 2nd edition, 2000.
[3] P. Erdös, A. W. Goodman, and L. Pósa, The representation of a graph by set intersections, Canad. J. Math. 18: 106-112, 1966. doi:10.4153/CJM-1966-014-3
[4] S. McGuinness. The greedy clique decomposition of a graph. J. Graph Theory, 18: 427-430, 1994. doi:10.1002/jgt.3190180412
[5] T. Sousa. Friendship decompositions of graphs. Discrete Math., 308(15): 3352-3360, 2008. doi:10.1016/j.disc.2007.06.042
NOTES
*This work was partially supported by Financiamento Base 2010 ISFL-1-297 from FCT/MCTES/PT.

