Open Journal of Discrete Mathematics
Vol.1 No.2(2011), Article ID:5738,4 pages DOI:10.4236/ojdm.2011.12008
Log-Time Sampling of Signals: Zeta Transform*
1Department of Applied Physics, the University of Eastern Finland, Kuopio, Finland
2VTT Technical Research Centre of Finland, Espoo, Finland
E-mail: hannu.olkkonen@uef.fi
Received March 3, 2011; revised April 15, 2011; accepted April 23, 2011
Keywords: Sampling, z-transform, zeta function
Abstract
We introduce a general framework for the log-time sampling of continuous-time signals. We define the zeta transform based on the log-time sampling scheme, where the signal 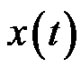 is sampled at time instants
is sampled at time instants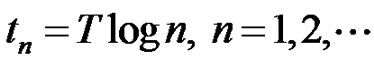 . The zeta transform of the log-time sampled signals can be described by a linear combination of Riemann zeta function, which firmly joins the log-time sampling process to the number theory. The instantaneous sampling frequency of the log-sampled signal equals
. The zeta transform of the log-time sampled signals can be described by a linear combination of Riemann zeta function, which firmly joins the log-time sampling process to the number theory. The instantaneous sampling frequency of the log-sampled signal equals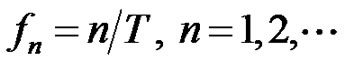 , i.e. it increases linearly with the sampling number. We describe the properties of the log-sampled signals and discuss several applications in nonuniform sampling schemes.
, i.e. it increases linearly with the sampling number. We describe the properties of the log-sampled signals and discuss several applications in nonuniform sampling schemes.
1. Introduction
Data acquisition techniques are usually based on the sampling of the signal 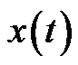 at equidistant time instants
at equidistant time instants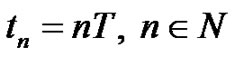 , where
, where 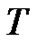 is the sampling period. This yields the discrete-time signal
is the sampling period. This yields the discrete-time signal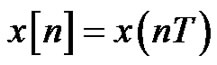 , which is usually treated using the z-transform
, which is usually treated using the z-transform
 (1)
(1)
The z-transform is an important tool in designing discrete-time signals and systems similarly as the Laplace transform in continuous-time domain. The variable z in the z-transform and the variable s in the Laplace-transform are related as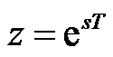 , which however, does not allow unique mapping between the complex z and s planes.
, which however, does not allow unique mapping between the complex z and s planes.
In this work we consider the log-time sampling scheme, where the discrete samples are measured at logarithmically spanned sampling instants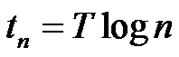 ,
,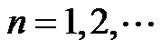 . This paper serves as a general framework for the log-time sampling process and we only discuss applications. We first describe the z-transform of the log-time sampling process and show the connection between the Riemann zeta function. Then we introduce the zeta transform and deduce the zeta transform of the continuous-time waveforms. Further, we show that the log-time sampled signals obey the convolution property and discuss the potential applications related to nonuniform sampling schemes.
. This paper serves as a general framework for the log-time sampling process and we only discuss applications. We first describe the z-transform of the log-time sampling process and show the connection between the Riemann zeta function. Then we introduce the zeta transform and deduce the zeta transform of the continuous-time waveforms. Further, we show that the log-time sampled signals obey the convolution property and discuss the potential applications related to nonuniform sampling schemes.
2. Theoretical Considerations
2.1. Log-Time Sampling Scheme
The log-time sampling of the continuous-time causal signal  is based on the convolution
is based on the convolution
 (2)
(2)
where the Dirac distribution is defined as
 (3)
(3)
By shortly denoting  the integral transform of (2) yields
the integral transform of (2) yields
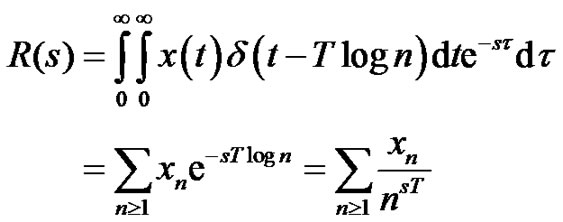 (4)
(4)
where 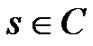 is the transform variable. In number theory the Riemann zeta function
is the transform variable. In number theory the Riemann zeta function 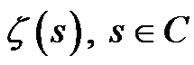 is defined as
is defined as
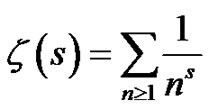 (5)
(5)
Due to close relationship with (5) we call (4) the zeta transform of the log-time sampling sequence
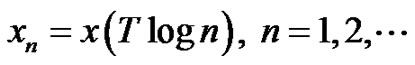
2.2. Zeta Transform for Continuous Waveforms
Let us consider the log-time sampling of the exponential signal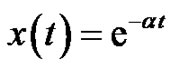 . We obtain
. We obtain
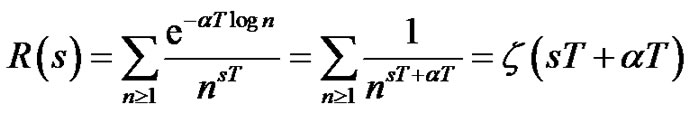 (6)
(6)
Table 1 gives the zeta transforms for some common continuous-time waveforms, which shows that the signals can be described by the linear combination of zeta functions. The direct computation of the  over the whole complex plane has the difficulty that the zeta function
over the whole complex plane has the difficulty that the zeta function 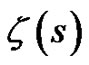 does not converge in the range
does not converge in the range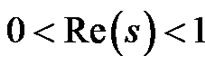 . This obstacle can be avoided by first computing the Dirichlet eta function
. This obstacle can be avoided by first computing the Dirichlet eta function
 (7)
(7)
which is convergent for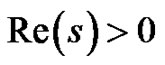 . The zeta function is then obtained from the simple relation
. The zeta function is then obtained from the simple relation
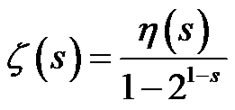 (8)
(8)
We may note that both the zeta and eta functions have a single pole at s = 1.
2.3. Instantaneous Frequency of the Log-Sampled Signals
The change of the sampling instant with the sampling number equals
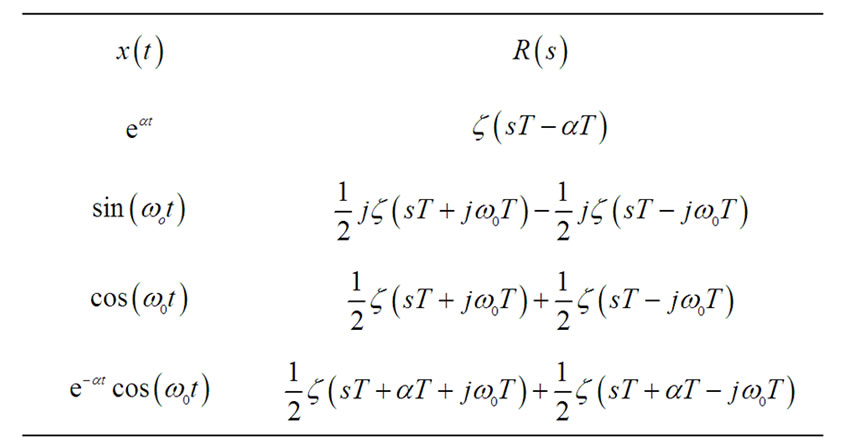
Table 1. Zeta transforms for continuous signals.
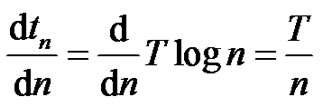 (9)
(9)
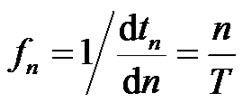 (10)
(10)
which indicates an interesting result that the instantaneous sampling frequency increases linearly with the sampling number.
The present log-time sampling scheme can be easily modified to fit a special application. For example in sequence
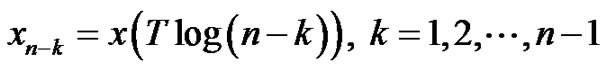 (11)
(11)
the sampling rate decreases linearly. In sequence
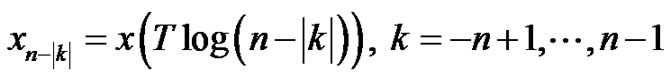 (12)
(12)
the sampling rate first increases to the maximum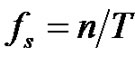 , then decreases.
, then decreases.
2.4. Logarithmic Time Delay
We may define the logarithmic time delay operator as
 (13)
(13)
which produces a time delay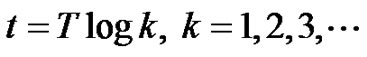 . The delayed signal is then
. The delayed signal is then
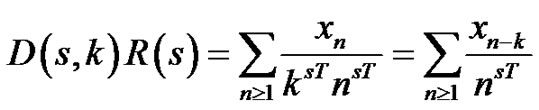 (14)
(14)
2.5. Convolution of the Log-Time Sampled Signals
Let us consider the convolution of the two log-time sampled signal sequences 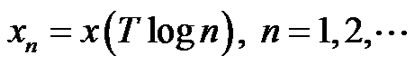 and
and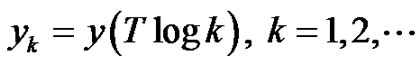 . We obtain the zeta transform of the sequence
. We obtain the zeta transform of the sequence ,
, 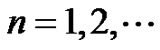
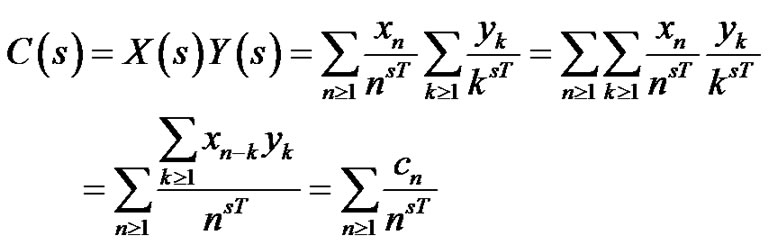 (15)
(15)
where
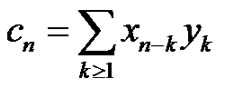 (16)
(16)
This is an important result indicating that the log-time sampled signal sequences obey the convolution property. This allows the fast computation of the convolution of the log-sampled sequences by the FFT algorithm.
3. Discussion
The present work shows several features of the log-time sampled signals. Probably the most crucial property is that the zeta transform of the analytic waveforms can be described by a linear combination of the Riemann zeta functions (Table 1). This firmly joins the log-time sampled signals to the number theory, where the zeta function has a privileged role. There are a vast number of algorithms for computation of the zeta functions [1]. Usually they are based on the accelerated zeta series or recursions. The application of the algorithms in microprocessor environment gives rise to a new kind of discrete-time filters for processing of log-time sampled signals.
In communication system analysis the transmission zeros have an important role. Let us suppose that the logarithmic sampling yields a sequence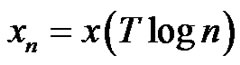 ,
, 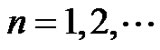 , which has the zeta transform R(s). Due to the Riemann hypothesis the zeta function
, which has the zeta transform R(s). Due to the Riemann hypothesis the zeta function 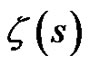 has nontrivial zeros in the complex plane only at a single line in
has nontrivial zeros in the complex plane only at a single line in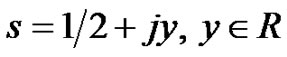 . For example, the discrete zeta transform of the sinusoidal waveform
. For example, the discrete zeta transform of the sinusoidal waveform 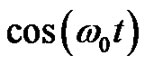 consists of the sum of two zeta functions having arguments
consists of the sum of two zeta functions having arguments 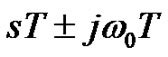 (Table 1). The transmission zeros can be solved by equalizing
(Table 1). The transmission zeros can be solved by equalizing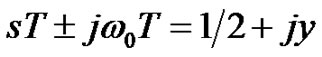 . The knowledge of the transmission zeros helps the analysis and design of the log-sampled signal processes, e.g. the analysis of the cross-talk between neighbouring channels. In parallel multi-channel information systems the transmission zeros, which are too close to each other may give rise to the distortion and interference.
. The knowledge of the transmission zeros helps the analysis and design of the log-sampled signal processes, e.g. the analysis of the cross-talk between neighbouring channels. In parallel multi-channel information systems the transmission zeros, which are too close to each other may give rise to the distortion and interference.
In this work we observed that the log-time sampled signal sequences obey the convolution property (15-16). This yields a plenty of tools for analysis. For example, the convolution of the two log-sampled sequences can be effectively computed by the FFT algorithm. Due to the log-time sampling the number of the measured data points and the computation time can be significantly reduced compared with the FFT of the equidistantly sampled data sequence.
An interesting result (10) in this work is the observation that the instantaneous frequency of the log-time sampled signals increases linearly with the sampling number. In time-frequency analysis of the log-time sampled signals the frequency scale is linearly increasing, which more dense compared with the wavelet analysis, where the frequency scale increases in octave scale.
The log-time sampling of several types of signals has clear advantages compared with the equidistant sampling scheme. The measurement of fast impulses is not manageable using equidistant sampling. A scheme based on the sampling with finite rate of innovation (FRI) has awoken interest in signal processing society [2,3]. The FRI methods are based on the idea that the signal is measured with an analog circuit network. The output of the sampling kernel is measured with an analog-to-digital converter and the original signal is reconstructed from the discrete samples. A competing approach for measurement of impulses would be the log-time sampling scheme. As an example we may consider the measurement of the short pulses in wireless ultra wide band (UWB) transmission system. The UWB impulses are measured with a network consisting sequential RC-filters [4]. By using the log-time sampling scheme the amplitude of the impulse is sampled with maximum rate, but the tail is sampled with slowing rate. This gives a considerable savings in memory space and fastens the reconstruction. One promising approach is the parallel sampling scheme [5], where the signal is sampled with the aid of parallel RC-filters. The reconstruction of the signal can be made at log-time instants and the reconstructed signal is readily allowed for treatment with zeta transform algorithms.
In this work we have only shortly outlined the properties the log-time sampling scheme and its relation to number theory. The present sampling scheme may yield more and more advanced applications of digital signal processors and VLSI devices in measurement and reconstruction of signals.
4. Acknowledgements
We are greatly indebted to the anonymous referee, whose comments significantly improved the manuscript.
5. References
[1] J. M. Borwein, D. M. Bradley and R. E. Crandall, “Computational Strategies for the Riemann Zeta Function,” Journal of Computational and Applied Mathematics, vol. 121, No.1-2, 2000, pp. 247-296. doi:10.1016/S0377-0427(00)00336-8
[2] M. Vetterli, P. Marziliano and T. Blu, “Sampling Signals with Finite Rate of Innovation,” IEEE Transactions on Signal Processing, vol. 50, no. 6, 2002, pp.1417-1428. doi:10.1109/TSP.2002.1003065
[3] I. Maravic and M. Vetterli, “Sampling and Reconstruction of Signals with Finite Rate of Innovation in the Presence of Noise,” IEEE Transactions on Signal Processing, vol. 53, no. 8, 2005, pp. 2788-2805. doi:10.1109/TSP.2005.850321
[4] J. T. Olkkonen and H. Olkkonen, “Reconstruction of Wireless UWB Pulses by Exponential Sampling Filter,” Wireless Sensor Network, Vol. 2, 2010, pp. 462-466. doi:10.4236/wsn.2010.26057
[5] H. Olkkonen and J. T. Olkkonen, “Measurement and Reconstruction of Transient Signals by Parallel Exponential Filters,” IEEE Transactions on Circuits and Systems II, vol. 57, no. 6, 2010, pp. 426-429. doi:10.1109/TCSII.2010.2048375
NOTES
*This work was supported by the National Technology Agency of Finland (TEKES).

