Optics and Photonics Journal
Vol.06 No.05(2016), Article ID:66926,14 pages
10.4236/opj.2016.65012
An Improved Design for an All-Optical Flip-Flop Based on a Nonlinear 3-Sections DFB Laser Cavity
Hossam Zoweil
City of Scientific Research and Technology Applications, Advanced Technology and New Materials Research Institute, Alexandria, Egypt

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 March 2016; accepted 27 May 2016; published 30 May 2016
ABSTRACT
A new all optical flip-flop based on a 3-sections nonlinear semiconductor DFB laser structure is proposed and simulated. The operation of the device does not require a holding beam. Electrical current injection into an active layer provides optical gain to the laser mode. The wave-guiding layer consists of a linear grating section centered between 2 detuned nonlinear grating sections. The average refractive index in the nonlinear sections is slightly higher than the refractive index of the middle section. A negative nonlinear refractive index coefficient exists along the nonlinear sections. In the “OFF” state, the DFB structure does not provide enough optical feedback to lase due to the detuned sections. At high light intensity in structure, “ON” state, detuning decreases and the DFB structure allows for a laser mode that sustains the decrease in detuning to exist. The nonlinearity is provided by direct photon absorption at the Urbach tail. Numerical simulations using GPGPU computing show nanoseconds transition times between “OFF” and “ON” states.
Keywords:
All-Optical Flip-Flop, Distributed Feedback Laser, Nonlinearity, Switching

1. Introduction
All-optical data packet routing and processing requires an all optical data memory element to store optical information related to the optical data packet, [1] . Performing optical data packet routing/switching in the optical domain eliminates the need for the conversion of the optical signal from optical domain to the electronic domain and vise-versa. Also, it increases processing speed and reduces the complexity of the system. Many types of all optical flip-flop are suggested and implemented. In [2] , an all optical flip-flop based on a micro disk laser where the two states correspond to clock-wise and anti-clock-wise mode is implemented. An all optical flip-flop based on coupled micro laser rings is implemented in [3] . Flip-flop based on a single DFB laser structure is shown in [4] . All optical flip-flops based on multi-mode interference bistable laser diode are described in [5] - [7] . All these flip-flops require a holding beam, or, some of them gererate output modes in both ON and OFF states. All optical flip-flops based on bistable laser diode are discussed in [8] [9] , and they do not require a holding beam. In [8] [9] , the flip-flop is Fabry-Perot laser cavity that includes a saturable absorber, where the optical loss in the cavity is reduced at high light intensity in the laser cavity. In [10] , an all optical flip-flop based on a DFB structutre with a periodic negative nonlinearity is simulated. The flip-flop does not require a holding beam, and it requires a periodic negative nonlinear coefficient that alters the grating strength which is difficult to fabricate. In [11] , an all optical flip-flop based on a chirped nonlinear DFB structure is simulated. In this structure, the chirped grating prevents lasing due to the lacking of an optical feedback (OFF state). The negative nonlinear coefficient increases in magnitude linearly along the structure. The chirp is reduced when high optical power exists in the structure (because the nrgative nonlinear coefficient reduces the revractive index along the structure gradually) and a laser mode builds up. The structure in [11] requires a gradual increase in the linear refractive index of the wave guiding layer which is difficult to achieve. Also, it requires a gradual increase in magnitude of the nonlinear coefficient along the wave-guiding layer. This design could be achieved by using multiple sections of different linear and nonlinear coefficients. Each section has constant linear refractive index and constant negative nonlinear coefficient. However each section has slightly different linear and nonlinear coefficient as both of them must increase gradually along the structure. This could be difficult to fabricate, and we look for another simpler design.
In this work, an improved design is introduced. The device design is symmetric and requires less injected current. A novel all-optical flip-flop based on a 3-sections nonlinear DFB laser structure is proposed. The device allows for a bistable operation as is [11] , but with a simpler structure. In the following sections the device operation is discussed, a mathematical model is introduced and solved numerically using Rung-Kutta method.
2. Device Configuration and Operation
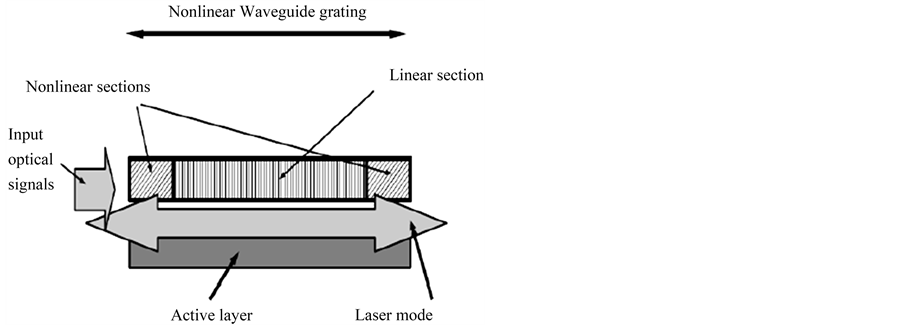
The device schematic is shown in Figure 1. It consists of a nonlinear 3-sections waveguide, and the optical gain is provided by electrical current injection to an active layer. The middle section is a phase-shifted grating. The distribution of refractive index grating and negative nonlinear coefficient is shown in Figure 2, 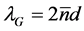 is the wavelength at the center of the reflection band of the grating, and d is the grating period. At low light intensity in the structure, the grating structure does not provide enough optical feedback to start a laser mode due to the detuning of the nonlinear sections (
is the wavelength at the center of the reflection band of the grating, and d is the grating period. At low light intensity in the structure, the grating structure does not provide enough optical feedback to start a laser mode due to the detuning of the nonlinear sections (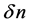 ) from the linear grating at the middle of the wave-guiding layer. When an input optical pulse is injected to the device, the detuning of the two nonlinear sections is reduced due to the negative nonlinear coefficient
) from the linear grating at the middle of the wave-guiding layer. When an input optical pulse is injected to the device, the detuning of the two nonlinear sections is reduced due to the negative nonlinear coefficient 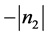 as in Figure 2. The flip-flop design investigated in this work has advantages over the the design described in [11] . First, while the structure in [11] has a gradual increase in the refrative index and the nonlinear coefficient along the waveguide, the structure introduced in this work has only
as in Figure 2. The flip-flop design investigated in this work has advantages over the the design described in [11] . First, while the structure in [11] has a gradual increase in the refrative index and the nonlinear coefficient along the waveguide, the structure introduced in this work has only
Figure 1. Device schematic.
Figure 2. Refractive index distribution in the wave-guiding layer,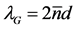 ; (a) linear, (b) non-linear.
; (a) linear, (b) non-linear.
two nonlinear sections of constant refractive index. Hence the structure shown in this article is easier in fabication. Second, the structure shown in [11] is not symmetric; in the ON state the output laser powers from both ends are not equal in steady state, however the structure studied in this article is symmetric. In steady state (in the ON state) the output optical power from both ends, of the suggested device, are equal. Also, the device investigated in [11] requires a high a injected current because in the OFF state the feedback grating is a chirped grating, and it requires high optical power and high injected current to reduce the chirp and to achieve lasing in the ON state. However in this work, in the OFF state, the feedback grating are not shirped but detuned, and the feedback grating sections require less injected current to achieve the lasing in the ON state.
Schematic of the device is shown in Figure 1. The refractive index distribution along the non-linear wave-guiding layer is shown in Figure 2. Electrical current injected to the active layer provides the optical gain. The device requires large negative nonlinear coefficient in the nonlinear grating sections. The negative nonlinear coefficient at the two nonlinear sections is provided by direct photon absorption at the Urbach tail, Figure 3. Part of the photons propagating in the device is absorbed and generates electron-hole pairs. The electron-hole pairs generated reduce the refractive index at incident photon energies slightly less than the semiconductor band gap energy [12] . At low light intensity in the device, due to detuning of the two nonlinear sections from the center linear grating part, the DFB structure does not provide enough optical feedback to initiate a laser mode. To switch the device “ON”, an optical “Set” pulse of photon energy slightly less than the band-gap energy of the nonlinear section of the waveguide (photon energy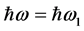 , Figure 3) is injected into the device. Part of the injected photons is absorbed (by direct absorption) and generate electron-hole pairs that reduce the average refractive index (and the detuning) of the nonlinear sections. Hence, both nonlinear sections contribute to the optical feedback along the structure. As the optical feedback increases, the DFB structure allows for an optical laser mode to exist. The optical laser mode intensity maintains the reduction in refractive index in the nonlinear sections, and the laser mode persists. The device is switched the OFF by cross gain modulation (XGM). An optical “Reset” pulse at lower frequency (
, Figure 3) is injected into the device. Part of the injected photons is absorbed (by direct absorption) and generate electron-hole pairs that reduce the average refractive index (and the detuning) of the nonlinear sections. Hence, both nonlinear sections contribute to the optical feedback along the structure. As the optical feedback increases, the DFB structure allows for an optical laser mode to exist. The optical laser mode intensity maintains the reduction in refractive index in the nonlinear sections, and the laser mode persists. The device is switched the OFF by cross gain modulation (XGM). An optical “Reset” pulse at lower frequency ( ,
, Figure 3) is injected to the device. The pulse reduces the optical gain at
Figure 3) is injected to the device. The pulse reduces the optical gain at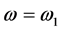 , and the laser mode decays. The electron-hole pairs generated by the optical pulse at
, and the laser mode decays. The electron-hole pairs generated by the optical pulse at 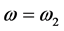 are much less than the electron-hole pairs generated at
are much less than the electron-hole pairs generated at  due to lower direct absorption coefficient at
due to lower direct absorption coefficient at 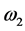 as in Figure 3. When the laser mode decays by XGM, the electron-hole density generated by the laser mode at
as in Figure 3. When the laser mode decays by XGM, the electron-hole density generated by the laser mode at  decays by time. The average refractive index in the nonlinear sections increases, and these two sections become detuned from the phase-shifted grating at the middle section. The optical feedback, in
decays by time. The average refractive index in the nonlinear sections increases, and these two sections become detuned from the phase-shifted grating at the middle section. The optical feedback, in
Figure 3. Direct absorption loss at Urbach tail; 

this case, is reduced and the optical laser mode is not allowed to build up. In this work, 




3. Mathematical Model and Simulation Parameters
The laser mode in the device is modeled as 2 counter propagating modes. Coupled mode equations are used to model laser mode in the device [11] [14] . The electric field in the device is presented as: 













Equations (1) and (2) represent the coupled mode equations of the laser mode and the “Set” pulse. Equation (3) presents the “Reset” pulse. Equations (4) and (5) describe detuning, loss and coupling coefficients (


c is the velocity of light in vacuum, and 








































It was assumed, in the simulations,
The system of differential equations is solved using Rung-Kutta technique. The length of the device is divided into 80 sections.
General purpose graphics processing unit (GPGPU) computing is used to perform long simulation time (150 nanosecond). This is done by distributing the computation load along the length of the device among 80 parallel threads that compute the forward and backward fields in the next time step simultaneously. The parallel computation decreases the computation time. The numerical simulations use a PC (processor: intel Core i3-4130 CPU at 3.40 GHz ´ 4, and 32 GB RAM) and graphics processing unit (GPU) Nvidia GeForce GTX 670. The program is coded using Cuda C, [18] .
In the following sections, optical bi-stability and ON/OFF switching dynamics in time domain are investigated by solving the mathematical model numerically.
4. Numerical Simulations and Discussion
In the following simulations, the output optical laser power is

the meduim. The output power is normalised to

Table 1. Simulation parameters.
the Electric fields are normalised to










4.1. Current versus Optical Laser Mode Power Bi-Stability
Optical output mode power versus electrical current injected bi-stability is calculated as follow. The injected current to the device is increased from 0 to 0.08 Ampere in 75 nanosecond linearly. Then, the current is decreased linearly till it reaches 0 in an another 75 nanosecond. Optical bi-stability loop is shown in Figure 4. To insure bi-stable operation of the device, the injected current 









4.2. OFF and ON States
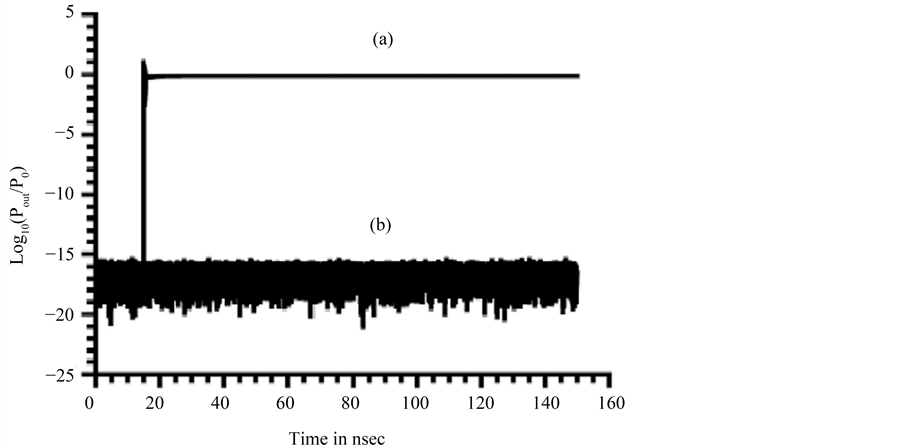
The output optical powers at the ON and at the OFF states are simulated for 150 nsec to insure the stability of the output in each state.
Figure 4. Bi-stability loop; current versus output optical power at
The device is switched ON by a Set pulse at 



A part of the input pulse energy (photons) is absorbed in the nonlinear wave-guiding sections. It generates electron-hole pairs that reduce the refractive index in each nonlinear section. This decrease in refractive index decreases the detuning in these sections. Hence, the reflection band of each nonlinear section starts to overlap with the reflection band of the middle phase-shifted grating. The optical feedback (reflections) from both nonlinear sections increases, an optical laser mode builds up in the central part of the nonlinear grating section. The optical power of the laser mode maintains the changes in the refractive index in both nonlinear sections. Figure 6 shows the evolution of electron-hole pairs density 










4.3. Set-Reset Operation
Set-Reset operation is simulated in time domain for 22.5 nsec. At t = 22.5 nsec from the start of simulation time, an input optical pulse (Set pulse) at 







The output optical power is shown in Figure 10. The Reset pulse reduces the optical gain at 


Figure 5. Output optical power in (a) ON state, and (b) OFF state.
Figure 6. ON state; Electron-hole pairs density at 
4.4. Multiple Set-Reset Operations
Multiple Set/Reset operations are simulated for 150 nsec.
The input pulses are shown in Figure 13. Input pulses (at











Figure 7. ON state; Electron-hole pairs density in the active layer at
Figure 8. Distribution of refractive index change in ON state, and OFF state.
in the time interval between the RESET pulse and the next SET pulse, and after the multiple operations elapse. This is the same value in the OFF state. During the RESET operations 
5. Conclusion
In this work, a new, improved all-optical flip-flop based on a nonlinear 3-sections DFB laser structure was investigated. The device has advantages over work shown in [11] ; the device is symmetric and could be fabricated easiley. The device could be implemented using InGaAsP semiconductor alloy. Negative nonlinearity is implemented by direct absorption of a part of the incident photons at the Urbach tail. Graphics Processing Unit (GPU)
Figure 9. Set pulse (first pulse), and reset pulse (second pulse).
Figure 10. Output optical power during Set/Reset operation.
Figure 11. 

Figure 12. 

Figure 13. Input pulses for multiple Set/Reset operations.
Figure 14. Output optical power for multiple Set/Reset operations at
Figure 15. 

Figure 16. 

is used to solve the mathematical model using parallel computing to be able to decrease the integration step and to be able to reduce the simulation time. The switching dynamics are investigated and show switching between different states in nanosecond time scale. The device is switched ON with a 



Cite this paper
Hossam Zoweil, (2016) An Improved Design for an All-Optical Flip-Flop Based on a Nonlinear 3-Sections DFB Laser Cavity. Optics and Photonics Journal,06,87-100. doi: 10.4236/opj.2016.65012
References
- 1. Dorren, H.J.S., Hill, M.T., Liu, Y., Calabretta, N., Srivatsa, A., Huijskens, F.M., de Waardt, H. and Khoe, G.D. (2003) Optical Packet Switching and Buffering by Using All-Optical Signal Processing Methods. Journal of Lightwave Technology, 21, 2-12.
http://dx.doi.org/10.1109/JLT.2002.803062 - 2. Liu, L., Kumar, R., Huybrechts, K., Spuesens, T., Roelkens, G., Geluk, E.J., de Vries, T., Regreny, P., Thourhout, D.V., Baets, R. and Morthier, G. (2010) An Ultra-Small, Low-Power, All-Optical Flip-Flop Memory on a Silicon Chip. Nature Photonics, 4, 182-187.
- 3. Hill, M.Y., Dorren, H.J.S., de Vries, T., Leijtens, X.J.M., den Besten, J.H., Smalbrugge, B., Oei, Y.S., Binsma, H., Khoe, G.D. and Smit, M.K. (2004) A Fast Low-Power Optical Memory Based on Coupled Micro-Ring Lasers. Nature, 432, 206-208.
http://dx.doi.org/10.1038/nature03045 - 4. Huybrechts, K., Morthier, G. and Baet, R. (2008) Fast All-Optical Flip-Flop Based on a Single Distributed Feedback Laser Diode. Optics Express, 16, 11405-11410.
http://dx.doi.org/10.1364/OE.16.011405 - 5. Takenaka, M., Raburn, M. and Nakano, Y. (2005) All-Optical Flip-Flop Multimode Interference Bistable Laser Diode. IEEE Photonics Technology Letters, 17, 968-970.
http://dx.doi.org/10.1109/LPT.2005.844322 - 6. Jiang, H., Chaen, Y., Hagio, T., Tsuruda, K., Jizodo, M., Matsuo, S., Xu, J., Peucheret, C. and Hamamoto, K. (2011) All-Optical Flip-Flop Operation Based on Asymmetric Active-Multimode Interferometer Bi-Stable Laser Diodes. Optics Express, 19, B119-B124.
http://dx.doi.org/10.1364/OE.19.00B119 - 7. Takeda, K., Takenaka, M., Raburn, M., Kanema, Y., Barton, J.S., Song, X. and Nakano, Y. (2007) Dynamic Operation of All-Optical Flip-Flops with Distributed Bragg Reflectors for Self-Routing of 10-Gb/s Optical Packets. Japanese Journal of Applied Physics, 46, 1028-1032.
http://dx.doi.org/10.1143/JJAP.46.1028 - 8. Kawaguchi, H. (1997) Bistable Laser Diodes and Their Applications: State of the Art. IEEE Journal of Selected Topics in Quantum Electronics, 3, 1254-1270.
- 9. Odagawa, T. (1991) Bistable Semiconductor Laser Diode Device. US Patent No.: 5007061.
- 10. Zoweil, H. (2010) Theoretical Modeling of an Improved All-Optical Flip Flop Based on a Nonlinear Semiconductor Distributed Feedback Laser Structure. Applied Optics, 49, 5199-5204.
http://dx.doi.org/10.1364/AO.49.005199 - 11. Zoweil, H. (2015) Numerical Simulation of a Novel All-Optical Flip-Flop Based on a Chirped Nonlinear Distributed Feedback Semiconductor Laser Structure Using GPGPU Computing. Journal of Modern Optics, 62, 738-744.
http://dx.doi.org/10.1080/09500340.2015.1005186 - 12. Bennett, B.R., Soref, R.A. and Del Alamo, J.A. (1990) Carrier-Induced Change in Refractive Index of InP, GaAs, and InGaAsP. IEEE Journal of Quantum Electronics, 26, 113-122.
http://dx.doi.org/10.1109/3.44924 - 13. Adachi, S. (1992) Physical Properties of IIIV Semiconductor Compounds. John Wiley, Chichester.
- 14. Carrol, J., Whiteaway, J. and Plumb, D. (1998) Distributed Feedback Semiconductor Laser. IEE, London.
http://dx.doi.org/10.1049/PBCS010E - 15. Pankove, J.I. (1965) Absorption Edge of Impure Gallium Arsenide. Physical Review, 140, A2059-A2065.
http://dx.doi.org/10.1103/PhysRev.140.A2059 - 16. Dow, J.D. and Redfield, D. (1972) Toward a Unified Theory of Urbach’s Rule and Exponential Absorption Edges. Physical Review B, 5, 594-610.
- 17. Haug H., Ed. (1988) Optical Nonlinearities and Instabilities in Semiconductors. Academic Press, Inc., Mitchigan.
- 18. https://developer.nvidia.com/cuda-zone