Optics and Photonics Journal
Vol.05 No.07(2015), Article ID:58500,12 pages
10.4236/opj.2015.57023
Theoretical Introduction and Generation Method of a Novel Nondiffracting Waves: Olver Beams
Abdelmajid Belafhal, Lahcen Ez-Zariy, Salima Hennani, Hamid Nebdi
Laboratory of Nuclear, Atomic and Molecular Physics Department of Physics, Faculty of Sciences, Chouaïb Doukkali University, El Jadida, Morocco
Email: belafhal@gmail.com, ezzariy@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 June 2015; accepted 28 July 2015; published 31 July 2015
ABSTRACT
In this paper, we introduce a new class of scalar nondiffracting Helmholtz-equation solution. We demonstrate that this novel wave-equation solution has some specific orders; among these ordinary Airy beams which are regarded as the zeroth order. Moreover, a general expression of these novel beams, which are named Olver Beams and referred to OBs, is developed. The zeroth and the first high orders of the incident OBs are presented theoretically and numerically in this paper. Yet, based on a computer generated holograms method, the generation’s masks of the Finite OBs in first orders are given in this work. Also, the incident transverse intensity distribution in 1-D and 2-D of the first orders of OBs is performed.
Keywords:
Olver Beams, Airy Beams, Fourier Transform, Masks

1. Introduction
Olver beams which are the subject of this work, are proved to be a new class of nondiffracting beams and therefore as solution of scalar nondiffracting Helmholtz-equation. This new beams family is defined for the non-negative integer index beam’s order m. The zeroth order of this class of beams has described the ordinary Airy beams, which were introduced firstly by Berry et al. [1] in 1979, in the context of quantum mechanics. In this last work, the authors were interested to explain all the propagation properties of the Airy wave packet. The latter is a solution of Schrödinger equation which is equivalent to the equation of the linear propagation under the paraxial approximation of diffraction. The Airy beams class had attracted interest since their introduction theoretically and experimentally by Siviloglu et al. [2] [3] in 2007. Recently, for physical realization, this beams family has been modulated by an exponential term to obtain the finite Airy beam which is expressed as a product of the classical Airy mode and the linear exponential function. For many reasons, researchers have tried to properly study these laser beams and to be interested in their most remarkable properties. These beams are already considered as a single type of nondiffracting beams that are currently described in literature as a one-dimensional system [2] -[10] . The concept of Airy beams has been deeply explored on optical transforms for light beams; Airy transform can be applied in optics laser in many contexts by using Fourier Transform, Hankel Transform and Hilbert Transform. These transforms are all useful in beam shaping, beam analysis, image processing and others [11] -[22] .
Since 2013, our research laboratory group has started its researches over the Airy class beams through different optical systems. At first, we found a theoretical formalism for the study of the propagation of these nondiffracting beams family through an ABCD optical system with a rectangular annular aperture [23] . Another study has demonstrated the propagation characteristics of Airy-Gaussian beams passing through a misaligned ABCD optical system with aperture [24] . Thereafter, our studies have gone further than the previous work to do the same study of the propagation through an optical ABCD system, but this time with a new form of Airy-Her- mite-Gaussian beam [25] . This series of studies continue to give an interesting work that explores another new form of Finite Airy-Gaussian-Hermite-Gaussian Beams propagating through a paraxial ABCD optical system [26] , which is a special case of the Olver beams.
The present work will be an extension of the study of nondiffracting Airy beams. We will give a general analytical expression of a novel beams family, called Olver beams and is a solution of Schrödinger equation. This solution can be expressed in terms of Olver functions obtained directly by solving Olver’s differential equation given by [27] :
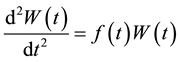 , (1)
, (1)
where
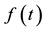 is a real continuous function equal to a constant factor that times a power of
is a real continuous function equal to a constant factor that times a power of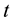 . The analysis of this function, which represents the solution of Equation (1), is the subject of the Olver beams that will be used in a large number of more general applications concerning their distributions through a different optical system. Therefore, the form of these solutions changes depending on the sign of t which will be discussed in the second part of this paper besides reporting the first idea of Olver optical beams. In the third part, we will give all the integral representations and analytical expressions of Olver functions noted as
. The analysis of this function, which represents the solution of Equation (1), is the subject of the Olver beams that will be used in a large number of more general applications concerning their distributions through a different optical system. Therefore, the form of these solutions changes depending on the sign of t which will be discussed in the second part of this paper besides reporting the first idea of Olver optical beams. In the third part, we will give all the integral representations and analytical expressions of Olver functions noted as
 of different orders m. Then we will introduce the finite Olver electrical field formulas and numerical representations of their corresponding intensity distributions for different orders m = 1, 2 and 3. Finally, in the fourth section of this report and by using a computer-generated holograms technique, we present the masks used in the experimental generation of the finite Olver beams. Also, in the same section we will draw all the masks of the finite Olver beams for each order m. Thanks to their alternative properties, below, we separate between four classes of Olver beams corresponding to different orders.
of different orders m. Then we will introduce the finite Olver electrical field formulas and numerical representations of their corresponding intensity distributions for different orders m = 1, 2 and 3. Finally, in the fourth section of this report and by using a computer-generated holograms technique, we present the masks used in the experimental generation of the finite Olver beams. Also, in the same section we will draw all the masks of the finite Olver beams for each order m. Thanks to their alternative properties, below, we separate between four classes of Olver beams corresponding to different orders.
2. Olver Beams Theory and Their Relationship with Olver’s Functions
2.1. Olver’s Equations and Their Solutions
The Airy function which is a special case of generalized Olver function at m = 0 is a solution of the scalar Helmholtz-equation and their generalization is also a solution of differential wave-equation. So, the Olver functions evolve according to the scalar wave-equation in terms of the variables

 (2)
(2)
whose solution is, if only if we consider that
 is a purely imaginary complex,
is a purely imaginary complex,
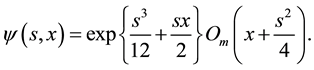 (3)
(3)
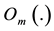 is the Olver function of order m, with
is the Olver function of order m, with
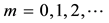 which would be calculated analytically for different orders. Equation (3) is verified directly by using the integral representation of the Olver function expressed as follows (Appendix A & B):
which would be calculated analytically for different orders. Equation (3) is verified directly by using the integral representation of the Olver function expressed as follows (Appendix A & B):
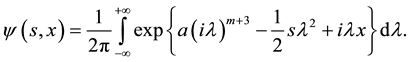 (4)
(4)
Our analysis suggests also a potential relationship which links the solutions of Olver’s equation with the Olver functions. It is the starting point for the discovery of Olver beams family using a well-known form of Olver’s ordinary differential equation in the unknown function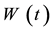 , given by Equation (1), when
, given by Equation (1), when
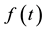 is expressed as:
is expressed as:
 (5)
(5)
where
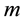 denotes a positive integer as
denotes a positive integer as . Equation (1) adopts as one standard solution according to the sign of
. Equation (1) adopts as one standard solution according to the sign of



Depending on the sign of the parameter
Case 1:
When the variable



where




with
Case 2:
On the contrary, when the variable



where




Case 3:
When the variable



With the use of Equation (6), one obtains

2.2. Introduction of Olver Beams as Nondiffracting Beams Family
In this part, we will include the exact analytical and illustrative graphs of Olver functions



with
For the reason to obtain the accurate analytical expression of this integral established in the Equation (13) which will be calculated according to the parity of

Case 1:
When the parameter


In this case,


After some calculations, we find

with
Case 2:
When the parameter


giving:

with
Case 3:
This case treats the condition



After developing this last equation, we find

with
Case 4:
In the last case, one takes




we find:

with
In this case, it is pointed that the zeroth-order of Olver beams corresponds to the pur Airy beam [1] .
3. Special Cases Representation
Based on the above formulas elaborated in Equations (15), (17), (19) and (21), the closed-forms analytical expressions of the first orders of Olver’s nondiffracting beams are given by:

In Figure 1, we present the one-dimensional distribution of Olver’s function for different orders m, as m = 0, 1, 2 and 3 determined by Equation (22).
A comparison is conducted between the ordinary Airy beam representation [28] and our zeroth-Olver function calculated at m = 0 by using Equation (22). This result validates the theoretical concept used to calculate Olver functions

We notice the appearance of some secondary lobes in the left of the central lobe for the even orders of the Olver beams. While we observe these sidelobes at the right of the central lobe for the odd orders. See Figures. (a-b)



4. Olver’s Holograms Masks
In this section, we will introduce how to generate the Olver beams in all orders by using a computer-generated
Figure 1. Distribution of Olver’s functions for various orders m.
holograms technique which is defined as a recording of the interference pattern between two light beams, making this technique an easily use full tool. The Fourier Transform (TF) provides a good understanding of Franhaufer diffraction for holograms. Hence, the result of this Franhaufer diffraction is proportional to the Fourier transform of the product of the input field (Gaussian beam) (Einp) and of the Hologram transmission function noted H . By producing such holograms, the transformation of the interference patterns is written as [29] [30] :

This transformation will be used to simulate the holographic masks illustrated in Figure 3, and expressed analytically for the Finite Olver beams for the first special orders as:

For the experimental realisation, one can use the proposed masks to elaborate the desired Finite Olver beams. Note that the first mask corresponds to the one used in [2] [3] .
5. Conclusion
In conclusion, a general analytical expression of the Olver beams (OBs) was devoted for various orders as a novel family class of conical beams and was considered as a generalization of the ordinary Airy beams. We had




Figure 2. 2D-Intensity distribution of Olver beams ((a); (c); (e); (g)) and their finite Olver beams ((b); (d); (f); (h)) for various orders: m = 0 ((a); (b)); m = 1 ((c); (d)); m = 2 ((e); (f)), m = 3 ((g); (h)).

Figure 3. Masks for generating the Finite Olver Beams (using Equation (24)) for different orders: (a) m = 0, (b) m = 1 and (c) m = 2.
demonstrated that the OBs were the solution of the scalar Helmholtz equation. Yet, in this work, the finite Olver beams are reported as pseudo-nondiffracting beams related to the OBs. We demonstrated the ability to generate and to produce this last class of optical beams using a computer-generated holograms technique. The obtained results provide more ideas for studying the propagation of the Olver beams and for examining their tuning properties through different optical systems.
Cite this paper
AbdelmajidBelafhal,LahcenEz-Zariy,SalimaHennani,HamidNebdi, (2015) Theoretical Introduction and Generation Method of a Novel Nondiffracting Waves: Olver Beams. Optics and Photonics Journal,05,234-246. doi: 10.4236/opj.2015.57023
References
- 1. Berry, M.V. and Balazs, N.L. (1979) Non-Spreading Wave Packets. American Journal of Physics, 47, 264-267. http://dx.doi.org/10.1119/1.11855
- 2. Siviloglou, G.A. and Christodoulides, D.N. (2007) Accelerating Finite Energy Airy Beams. Optics Letters, 32, 979-981. http://dx.doi.org/10.1364/ol.32.000979
- 3. Siviloglou, G.A., Broky, J., Dogariu, A. and Christodoulides, D.N. (2007) Observation of Accelerating Airy Beams. Physical Review Letters, 99, 213901. http://dx.doi.org/10.1103/PhysRevLett.99.213901
- 4. Chen, R.P., Zhong, L.X., Wu, Q. and Chew, K.H. (2012) Propagation Properties and M2 Factors of a Vortex Airy Beams. Optics & Laser Technology, 44, 2015-2019.
http://dx.doi.org/10.1016/j.optlastec.2012.03.038 - 5. Zhokovsky, K.V. and Dattoli, G. (2011) Evolution of Non-Spreading Airy Wave-Packets in Time Dependent Linear Potentials. Applied Mathematics and Computation, 217, 7966-7974.
http://dx.doi.org/10.1016/j.amc.2011.02.088 - 6. Khonina, S.N. (2011) Specular and Vortical Airy Beams. Optics Communication, 284, 4263-4271.
http://dx.doi.org/10.1016/j.optcom.2011.05.068 - 7. Eyyuboglu, H.T. (2013) Scintillation Behavior of Airy Beam. Optics & Laser Technology, 47, 232-236.
http://dx.doi.org/10.1016/j.optlastec.2012.08.029 - 8. Cheng, H., Zang, W., Zhou, W. and Tian, J. (2010) Analysis of Optical Trapping and Propulsion of Rayleigh Particles Using Airy Beam. Optical Society of America, 18, 20384.
http://dx.doi.org/10.1364/oe.18.020384 - 9. Deng, D. and Li, H. (2012) Propagation Properties of Airy-Gaussian Beams. Applied Physics B, 106, 677-681. http://dx.doi.org/10.1007/s00340-011-4799-2
- 10. Carvalho, M.I. and Facao, M. (2010) Propagation of Airy-Related Beams. Optical Society of America, 18, 21938-21949. http://dx.doi.org/10.1364/oe.18.021938
- 11. Deng, D. (2012) Propagation of Airy Beams through a Hard-Edged Aperture. Applied Physics B, 107, 195-200. http://dx.doi.org/10.1007/s00340-012-4899-7
- 12. Zhou, G., Chen, R. and Chu, X. (2012) Fractional Fourier Transform of Airy Beams. Applied Physics B, 109, 549-556. http://dx.doi.org/10.1007/s00340-012-5117-3
- 13. Jiang, Y., Huang, K. and Lu, X. (2012) The Optical Airy Transform and Its Application in Generating and Controlling the Airy Beam. Optics Communications, 285, 4840-4843.
http://dx.doi.org/10.1016/j.optcom.2012.08.003 - 14. Deng, D. and Guo, Q. (2009) Airy Complex Variable Function Gaussian Beams. New Journal of Physics, 11, Article ID: 103029. http://dx.doi.org/10.1088/1367-2630/11/10/103029
- 15. Han, D., Liu, C. and Lai, X. (2012) The Fractional Fourier Transform of Airy Beams Using Lohmann and Quadratic Optical Systems. Optics & Laser Technology, 44, 1463-1467.
http://dx.doi.org/10.1016/j.optlastec.2011.12.017 - 16. Liu, X., Li, J., Chen, H. and Fan, Y. (2013) The Deflected Angle and Reflected Displacement of Airy Beams. Optik, 124, 6519-6522. http://dx.doi.org/10.1016/j.ijleo.2013.05.044
- 17. Broky, J., Siviloglou, G.A., Dogariu, A., and Christodoulides, D.N. (2008) Self-Healing Properties of Optical Airy Beams. Optics Express, 16, 12880-12891. http://dx.doi.org/10.1364/OE.16.012880
- 18. Wen, W., Lu, X., Zhao, C. and Cai, Y. (2014) Propagation of Airy Beam Passing through the Misaligned Optical System with Hard Aperture. Optics Communications, 313, 350-355.
http://dx.doi.org/10.1016/j.optcom.2013.10.056 - 19. Liu, Z. and Zhao, D. (2014) Propagation of Airy-Related Beams Generated from Flat-Topped Gaussian Beams through a Chiral Slab. Optics and Lasers in Engineering, 52, 13-18.
http://dx.doi.org/10.1016/j.optlaseng.2013.07.011 - 20. Chen, C., Yang, H., Kavehrad, M. and Zhou, Z. (2014) Propagation of Radial Airy Array Beams through Atmospheric Turbulence. Optics Communications, 52, 106-114.
http://dx.doi.org/10.1016/j.optlaseng.2013.07.003 - 21. Cheng, K., Zhong, X. and Xiang, A. (2014) Propagation Dynamics, Poynting Vector and Accelerating Vortices of a Focused Airy Vortex Beam. Optics & Laser Technology, 57, 77-83.
http://dx.doi.org/10.1016/j.optlastec.2013.09.039 - 22. Deng D., Du S. and Guo, Q. (2013) Energy Flow and Angular Momentum Density of Non Paraxial Airy Beams. Optics Communications, 289, 6-9. http://dx.doi.org/10.1016/j.optcom.2012.09.007
- 23. Ez-zariy, L., Nebdi, H., Boustimi, M. and Belafhal, A. (2014) Transformation of a Two-Dimensional Finite Energy Airy Beam an ABCD Optical System with a Rectangular Annular Aperture. Physical and Chemical News, 73, 39-51.
- 24. Ez-zariy, L., Hennani, S., Nebdi, H. and Belafhal, A. (2014) Propagation Characteristics of Airy-Gaussian Beams Passing through a Misaligned Optical System with Finite Aperture. Optics and Photonics Journal, 4, 325-336. http://dx.doi.org/10.4236/opj.2014.411033
- 25. Ebrahim, A.A.A., Ez-zariy, L., Boustimi, M., Chafiq, A., Nebdi, H. and Belafhal, A. (2014) Diffraction of Finite Airy-Hermite-Gaussian Beams by an Apertured Misaligned Optical System. Physical and Chemical News, 73, 21-29.
- 26. Alaidi, I., Boustimi, M., Nebdi, H. and Belafhal, A. (2014) Propagation through a Paraxial ABCD Optical System of a Novel Beams Family: Finite Airy-Gaussian Hermite-Gaussian Beams. Physical and Chemical News, 73, 10-13.
- 27. Olver, F.W.J. (1975) Connection Formulas for Second-Order Differential Equations with Multiple Turning Points. SIAM Journal on Mathematical Analysis, 8, 127-154. http://dx.doi.org/10.1137/0508009
- 28. Bandres, M.A. and Gutierrez-Vega, J.C. (2007) Airy-Gauss Beams and Their Transformation by Paraxial Optical Systems. Optics Express, 15, 16719-16728. http://dx.doi.org/10.1364/OE.15.016719
- 29. He H., Heckenberg, N.R. and Dunlop, H.R. (2007) Optical Particle Trapping with Higher-order Doughnut Beams Produced Using High Efficiency Computer Generated Holograms. Journal of Modern Optics, 42, 217-223. http://dx.doi.org/10.1080/09500349514550171
- 30. Carpentier, A.V., Michinel, H., Salgueiro, J.R. and Olivieri, D. (2008) Making Optical Vortices with Computer-Generated Holograms. American Journal of Physics, 76, 916-921.
http://dx.doi.org/10.1119/1.2955792 - 31. Vallée, O. and Soares, M. (2004) Airy Functions and Applications to Physics. Imperial College Press, London. http://dx.doi.org/10.1142/p345
- 32. Gradshteyn, I.S. and Ryzhik, I.M. (1994) Tables of Integrals Series and Products. 5th Edition, Academic Press, New York.
- 33. Abramowitz, M. and Stegun, I.A., Eds. (1964) Handbook of Mathematical Functions. Nath Bureau of Standards, Washington.
- 34. Andrews, L. and Philips, R. (1998) Laser Beams Propagation through Random Media. SPIE Press, Washington.
Appendix A
In this appendix, we present a numerical verification of our integral used in the theoretical part developed in this work giving us an adequate form of Olver functions. This integral has the following analytical expression:




with


This will allow us to validate our integral result defined in Equation (A.1).
Case 1:
In this case, the integral given by Equation (A.1) will be calculated analytically and validated numerically for m = 0. The formula of the ordinary Olver function calculated directly from Equation (A.2) is:

Analytically, for m = 0 and by using the following form of integration given by [31] -[34] :

we find

For m = 0, the integral given by Equation (A.1) is theoretically valid. For its numerical evaluation, we first calculate numerically the integral given by Equation (A.1) using the numerical Trapeze integration method. Then we simulate numerically the second part given as follows:

The integral given by Equation (1) is also validated numerically as shown in Figure A1. We note that the cal-
culation parameters chosen are given by:
Case 2:
For m = 1, the numerical evaluation of the integral expression given by Equation (A.1) is obtained by the same way as the first case, where m = 0 . We calculate numerically the integral given by Equation (A.1) by using the numerical Trapeze integration method, and then we simulate numerically the second part of the integral given as follows:

Figure A2 shows that our result is validated numerically by the following calculation parameters:
and s = 0.05.
Figure A1. Illustration of I0 calculated from Equation (A.1) and Equation. (A.6).
Figure A2. Illustration of I1 calculated from Equation. (A.1) and Equation. (A.7).
Case 3:
For m = 5 , as it has been done before for m = 0 and 1, we calculate numerically the integral expression presented in Equation (A.1) by using the numerical Trapeze integration method. Then, we simulate numerically the second part of the integral given as follows:

Figure A3 shows that the result of


In this appendix A, we tried to validate the integral given by Equation (A.1) with a numerical calculation. This will be useful to approach many theoretical optical problems concerning Olver expressions. We are confident to say that our results are satisfying.
Appendix B
We shall prove in this Appendix that the integral representation of Olver function is a solution of Schrödinger
Figure A3. Illustration of I5 calculated from Equation (A.1) and Equation (A.8).
equation for a particle with mass m, namely:

whose solution is :

where B is arbitrary constant.
According to the first term, we have

and the second term:

Finally, we prove that:

Using the following integral expression,

the analytical expression of
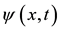

and for different values of the beam order, the probability density which is sketched in Figure B1, is given by:
Figure B1. Probability density for the Olver wave packet with
 (B.8)
(B.8)














