Optics and Photonics Journal
Vol. 3 No. 5 (2013) , Article ID: 36245 , 6 pages DOI:10.4236/opj.2013.35050
Effect of Partially Coherent Light on the Contrast of Speckle Patterns Obtained Using Digital Image Processing of Speckle Photography
Department of Physics, Faculty of Science, Helwan University, Cairo, Egypt
Email: Nasseramoustafa@yahoo.com
Copyright © 2013 Nasser A. Moustafa et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 13, 2013; revised June 17, 2013; accepted July 12, 2013
Keywords: Speckle Pattern; Surface Roughness; Partially Coherent Light
ABSTRACT
The paper is devoted to study theoretically, the effects of some parameters on the visibility of the speckle patterns. For this propose, a theoretical model for a periodic rough surface was considered. Using this theoretical model, the effects of grain height, its density, the band width and spectral distribution of the line profile (Gaussian and Lorentzian) illuminating a rough surface on the visibility of speckle pattern are investigated. An experimental setup was constructed to study the effect of surface roughness and coherence of the illuminating light beam on the contrast of speckle pattern. The general behavior of the experimental results, which agree with published data, is compatible with the new theoretical model.
1. Introduction
Speckle metrology techniques are promise to be a fruitful approach for solving a number of difficult problems in industry. The speckle pattern technique seems to be well suited for problems involving surface phenomena, fragile specimens and others [1-3]. A speckle pattern formed by partially spatially coherent light has been studied theoretically by many authors [4-6]. Fujii and Asakura [5] have developed a theoretical formulae for the intensity distribution of the speckle pattern as a function of the temporal coherence function and an equivalent optical transfer function. The relation between the statistical properties of the speckle pattern and the coherence characteristics of the illuminating source have been studied by Asakura et al. [7], Fujiwara et a1. [8] and Parry [9]. El-Nicklawy et al. [10] is devoted to the study of surface roughness from an interferometric point of view. It deals with a theoretical investigation of the intensity and visibility distribution of the speckle pattern resulting from the transmitted scattered radiation of strictlyand quasi monochromatic beams with Gaussian, Lorentzian and Voigte spectral profiles. The present work studied the effect of partially coherent light on the visibility of the speckle pattern. A theoretical model for a periodic rough surface was constructed. An equation for the visibility of speckle patterns is investigated by using partially coherent light.
2. Theoretical Model
Suppose a grain of dimension (a, b) is located on the surface of the transparent diffuser (Figure 1), where its center having the coordinates (xi, yi, 0). The wave function scattered from an element of dimensions (dxi, dyi, 0) located at position (x, y, 0) and illuminating a point P of coordinates (X, Y, Z) on a screen placed a distance apart from the diffuser is given by 
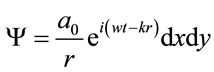 (1)
(1)
where 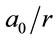 is the scattered amplitude per unit area from the diffuser,
is the scattered amplitude per unit area from the diffuser,
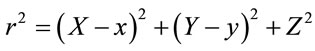 (2)
(2)
Let the grain under study is of dimensions a, b, and position (xi, yi, 0).
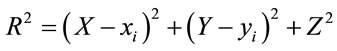 (3)
(3)
For 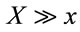 and xi , and
and xi , and 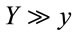 and yi we get:
and yi we get:
 (4)
(4)
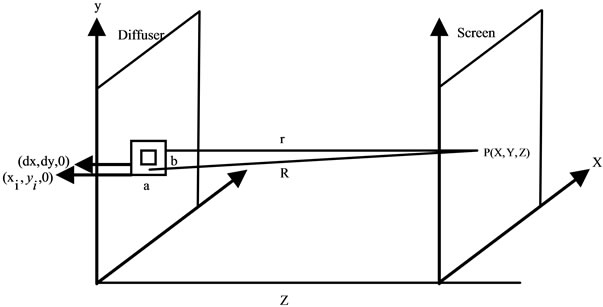
Figure 1. Construction of the theoretical model.
Using the Bernwlli inequality, one gets
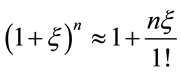 for
for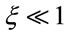 . Thus r can be written as
. Thus r can be written as
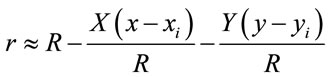 (5)
(5)
The integration of the wave amplitude given by Equation (5), over the entire area of a grain pensioned on (xi, yi, 0) gives the resultant wave amplitude emitted from and reaching point P on the screen as
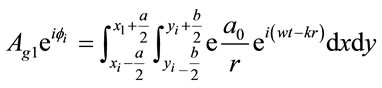 (6)
(6)
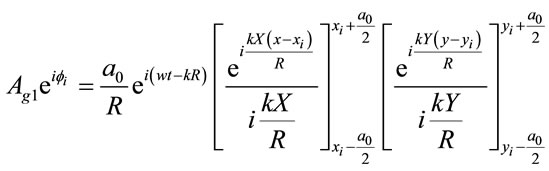 (7)
(7)
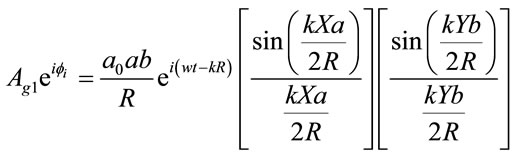 (8)
(8)
Let now another type of grain of thickness
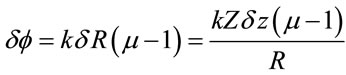
where  is the refracted index of used diffuser. Since
is the refracted index of used diffuser. Since 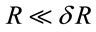 the amplitude is considered to be constant. Thus the wave amplitude reaching the point P from the second grain type will be given by:
the amplitude is considered to be constant. Thus the wave amplitude reaching the point P from the second grain type will be given by:
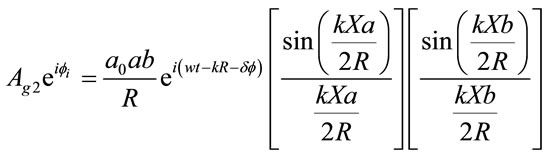 (9)
(9)
with

where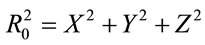 . Using the binomial expansion theorem
. Using the binomial expansion theorem 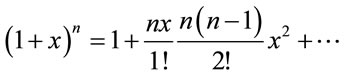 one gets after excluding the higher terms
one gets after excluding the higher terms 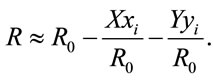
Let now an N × N number of grains of the first type per unit area be resident on the diffuser, thus the resultant wave amplitude reaching the point P on the screen will be given by:
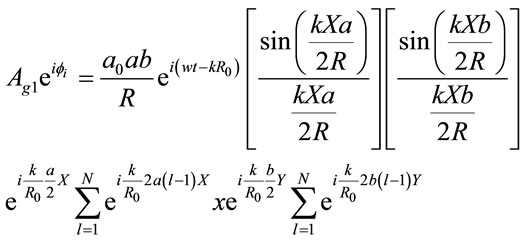 (10)
(10)
i.e.
 (11)
(11)
where , and
, and .
.
Similarly for the second type of the grains of number N × N per unit area, the resultant wave reaching the point P will be given by:
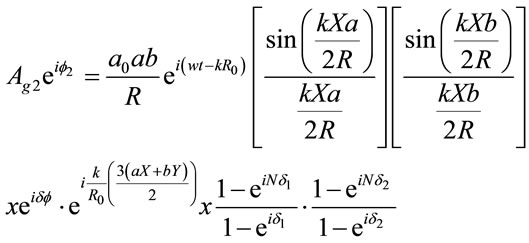 (12)
(12)
From Equations (11) and (12), it is seen that the phase difference between the two resultant waves 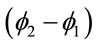 is given by:
is given by:
 (13)
(13)
Since
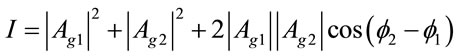 (14)
(14)
with 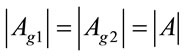 Equation (14) becomes
Equation (14) becomes
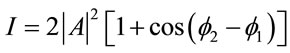 (15)
(15)
For 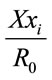 and
and , it follows
, it follows  and
and .
.
Setting Y = 0, and 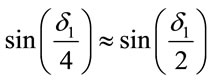
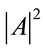 can be rewrite in the form
can be rewrite in the form
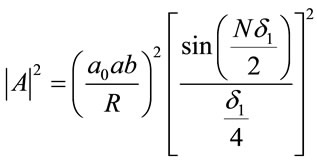 (16)
(16)
with ,
,
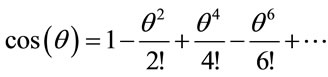
and
 (17)
(17)
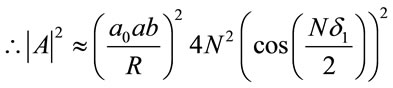 (18)
(18)
Thus the intensity can be written as
 (19)
(19)
Setting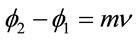 , where
, where
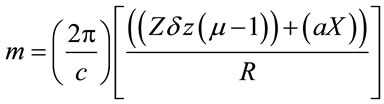 (19)
(19)
and , where
, where  (21)
(21)
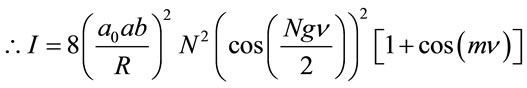 (22)
(22)
In the forgoing derivation, monochromatic irradiation of the rough surface was considered. In the paragraph to follow, the rough surface will be assumed to be non-monochromatic having different spectral distribution.
2.1. Gaussian Spectral Distribution
Assuming a symmetrical spectral line profile around 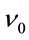 having a half width
having a half width 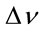 and given by the
and given by the
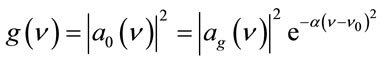 (23)
(23)
to irradiate the rough surface of the target where 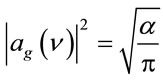 and
and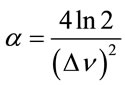 .
.
The intensity on the screen might be given by:
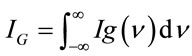 (24)
(24)
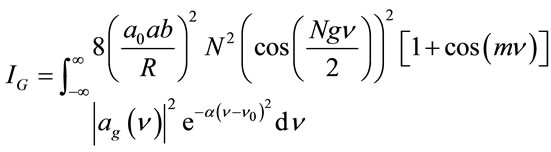 (25)
(25)
Setting

 ,
,  and
and  .
.
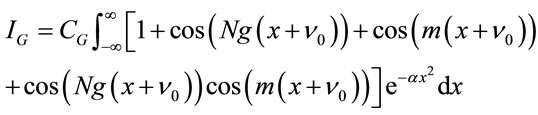 (26)
(26)
The integration of (26) gives, with  the following expression for the intensity distribution
the following expression for the intensity distribution
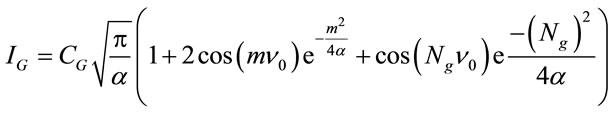 (27)
(27)
From (27) it is obvious that the intensity reaches its maximum as , and its minimum as
, and its minimum as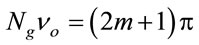 , with
, with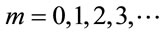 . Considering the above conditions for maximum and minimum intensity in (27) and setting the obtained expressions for
. Considering the above conditions for maximum and minimum intensity in (27) and setting the obtained expressions for 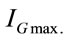 and
and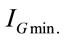 , one obtains,
, one obtains,
 (28)
(28)
2.2. Lorentzian Spectral Distribution
In this case it is assumed that a symmetrical spectral line profile around  following a Lorentizian profile function,
following a Lorentizian profile function,
 (29)
(29)
where 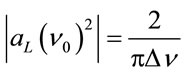
The intensity distribution is
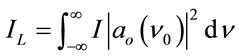 (30)
(30)
 (31)
(31)
where 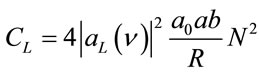
For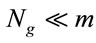 Then IL can be written as
Then IL can be written as
 (32)
(32)
From (32) it is obvious that the intensity is a maximum as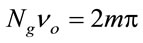 , and its minimum as
, and its minimum as , with
, with . Setting the above conditions in (32), one gets after determining
. Setting the above conditions in (32), one gets after determining 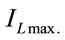 and
and 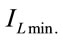 the following equation for the visibility
the following equation for the visibility
 . (33)
. (33)
3. Results and Discussion
To illustrate the dependence of the visibility on the grain height (surface roughness, the spectral half width, and the density of the grains, Equations (28) and (33) are computed for great distance between the diffuser and the screen, this distance chosen in the computation to be equal 400 cm. The area of the diffuser is constant = 1 cm2. Figure 2 shows the obtained results between the visibility of the speckle patterns and the spectral half width. The calculation was carried out considering the grain height and height to be 106 in cm2 and 50 μm respectively. From the figure it is evident that the visibility of Gaussian distribution is greater than that obtained from Lorentzian one considers the same half width is due to the higher effective spectral band width in the Lorentzian distribution which is larger than that in the case of the Gaussian one. The obtained behavior is in agreement with experimental data given in [6,11,12].
At a grain height of 10 μm, a spectral half width of 1012 Hz and varying grain width, Equations (28) and (33) were computed to study the effect of the grain density on the visibility of speckle patterns. Figure 3 shows the
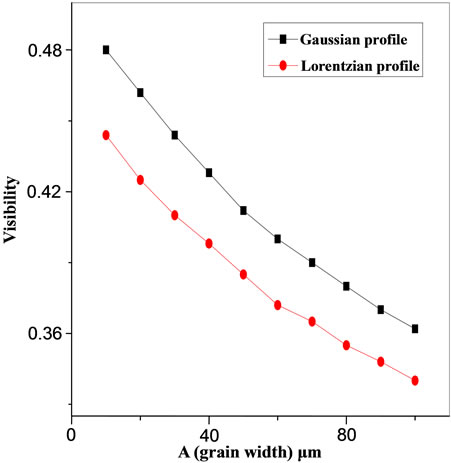
Figure 2. The visibility of speckle patterns versus the spectral half width Δν with spectral line shape as a parameter. The results are obtained considering the grain density to be 106 in cm2, the grain height to be 50 µm.
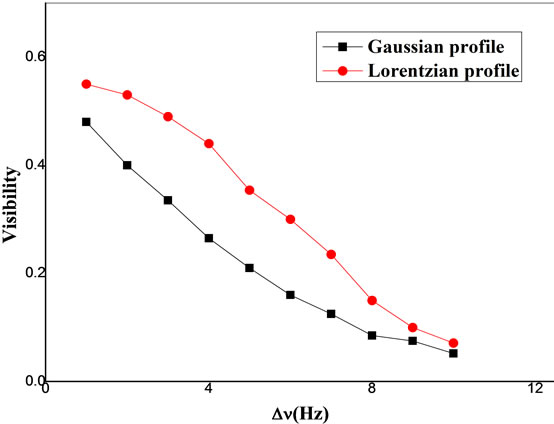
Figure 3. The visibility of the speckle patterns versus the grain width for the case of the Gaussian and Lorentzian profiles. The results are obtained for a grain height of 10 µm and spectral half width of 1012 Hz.
dependence of the visibility of speckle patterns on the grain width in case of Gaussian and Lorentzian profiles. It is evident that the greater density of the grains yields higher visibility of the speckle patterns. This behavior can be interpreted by the following: By increasing the density, the randomization in difference between the interfering beam become smaller leading to increase the visibility.
By keeping grain width equals 10μm and varying the grain height, Equations (28) and (33) were computed also to study the effect height on the visibility of the speckle patterns. Figure 4 shows the dependence of the visibility of speckle patterns on the grain height in case of Gaussian and Lorentzian spectral distributions at Δv = 1012 Hz. Figure 5 shows also the same, but for the case of Gaussian and Lorentzian spectral distributions at Δv = 1013 Hz. It is evident that by increasing the half width of the ra-
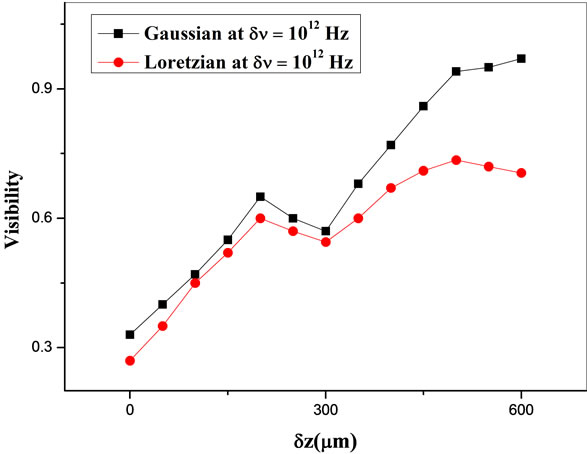
Figure 4. The visibility of the speckle patterns versus the grain height calculated for the case of Gaussian and Lorentzian profiles of δυ = 1012 Hz. The results are obtained for a grain density of 106 in cm2.
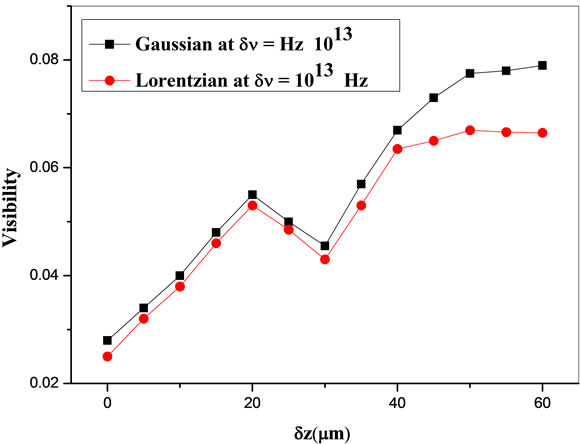
Figure 5. The visibility of the speckle patterns versus the grain height calculated for the case of Gaussian and Lorentzian profiles of δυ = 1013 Hz. The results are obtained for a grain density of 106 in cm2.
diation, the visibility of speckle patterns decreases. It is due to the inverse dependence of the degree of coherence of the light beam and its half width.
4. Experimental Verification
To verify the theoretical model an experiment as shown in Figure 6 was carried out using a partially coherent light obtained from a mercury lamp. The collimated light illuminates a diffusely transmitting object having different surface roughnesses. The obtained speckle intensity distributions were captured by a webcam (digital camera). To find the relation between the speckle intensity fluctuation and the surface roughness, the surface roughnesses of these objects was precisely mechanically measured beforehand by suing a stylus instrument. Figure 7 shows the obtained speckle pattern from partially
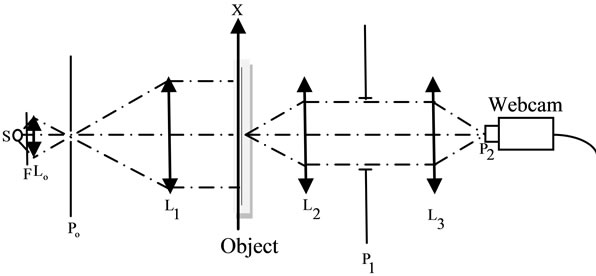
Figure 6. The experimental setup used for the verification of the theoretical model.

Figure 7. The obtained speckle pattern from partially coherent light.
coherent light.
By using software program (Image J), the value of the mean intensity 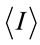 and the standard deviation σi of the speckle pattern was obtained and substituted in the contrast equation.
and the standard deviation σi of the speckle pattern was obtained and substituted in the contrast equation.
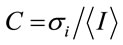 (34)
(34)
Figure 8 shows the dependence of the speckle patterns contrast on the surface roughness obtained from the two spectral lines of the Hg lamp (the green and yellow line). To increase the range of spectral half width, we used the setup in Figure 9. As we can see from the figure, the collimated light illuminates a diffraction grating D. The spectrum of Halogen lamp appears beyond the diffraction grating. By using a rectangle aperture, we can select bands with different widths. For each band width we repeat the previous experimental procedures. Figure 10 shows the dependence of the speckle patterns contrast on the surface roughness for different spectral half widths of values 2.9 × 1013 Hz, 2.59 × 1013 Hz, 1.857 × 1013 Hz, 1.295 × 1013 Hz respectively.
5. Conclusion
Effect of partially coherent light on the visibility was carried out. A theoretical model for a periodic rough sur-
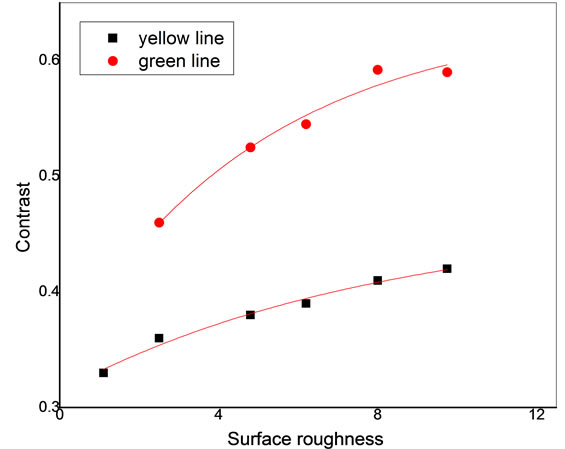
Figure 8. The relation between speckle patterns contrast and surface roughness.
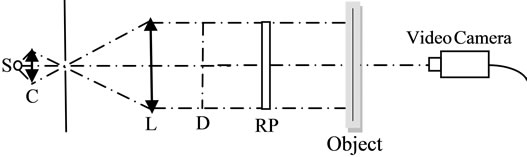
Figure 9. The experimental setup used to increase the range of the spectral half width.
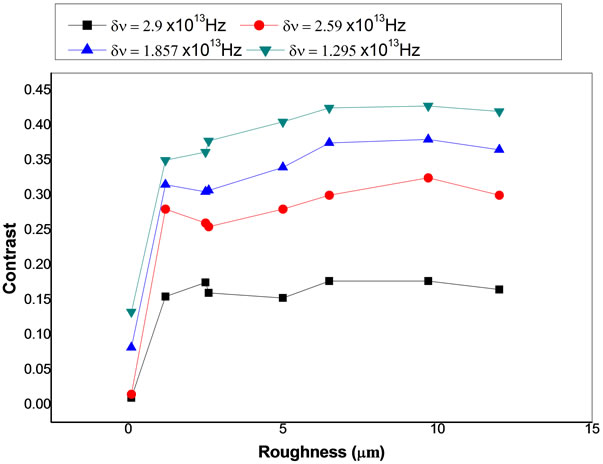
Figure 10. The relation between the speckle patterns contrast and surface roughness with Δν = 2.9 × 1013 Hz, 2.59 × 1013 Hz, 1.857 × 1013 Hz, and 1.295 × 1013 Hz as a parameter.
face was constructed. Depending on the new theoretical model, an equation for the visibility of speckle patterns is investigated using partially coherent light. The general behavior of the experimental results, which agree with the published data, are in good agreement with the new theoretical model.
REFERENCES
- E. Archbuld, J. M. Burch and A. E. Ennos, “Recording of In-Plane Surface Displacement by Double-Exposure Speckle Photography,” Optica Acta, Vol. 17, No. 12, 1970, pp. 883-898. doi:10.1080/713818270
- K. R. Erf, “Speckle Metrology,” Chapter 4, Academic Press, New York, San Francisco, London, 1978.
- H. J. Tiziani, “Application of Speckling for In-Plane Vibration Analysis,” Optica Acta, Vol. 18, No. 12, 1971, pp. 891-902. doi:10.1080/713818406
- H. Fujii and T. Asakura, “Coherence Measurement of Quasi Monochromatic Thermal Light Using Speckle Patterns 1,” Optik, Vol. 39, 1973, pp. 99-117.
- H. Fujii and T. Asakura, “Coherence Measurement of Quasi Monochromatic Thermal Light Using Speckle Patterns II,” Optik, Vol. 39, 1973, pp. 284-302.
- H. Fujji and T. Asakura, “A Contrast Variation of Image Speckle Intensity under Illumination of Partially Coherent Light,” Optics Communications, Vol. 12, No. 1, 1974, pp. 32-38.
- T. Asakura, H. Fujii and K. Murata, “Measurement of Spatial Coherence Using Speckle Pattern,” Optica Acta, Vol. 19, No. 4, 1972, pp. 273-290. doi:10.1080/713818561
- H. Fujiwara, T. Asakura and K. Murata, “Some Effects of Spatial and Temporal Coherence in Holography,” Optica Acta, Vol. 17, No. 11, 1970, pp. 823-838. doi:10.1080/713818257
- C. Parry, “Some Effects of Temporal Coherence on the First Order Statistics of Speckle,” Optica Acta, Vol. 21, No. 10, 1974, pp. 763-772. doi:10.1080/713818852
- E. A. Guillemin, “The Mathematics of Circuit Analysis,” John Wiley and Sons, New York, 1951, p. 530.
- C. F. Cheng, C. X. Liu, N. Y. Zhang, T. Q. Jia, R. X. Li, and Z. Z. Xu, “Absolute Measurement of Roughness and Lateral-Correlation Length of Random Surfaces by Use of the Simplified Model of Image-Speckle Contrast,” Applied Optics, Vol. 41, No. 20, 2002, pp. 4148-4156. doi:10.1364/AO.41.004148
- H. Fujji and T. Asakura, “Statistical Properties of Image Speckle Patterns in Partially Coherent Light,” Nouvelle Revue d’Optique, Vol. 6, No. 1, 1975, pp. 5-14. doi:10.1088/0335-7368/6/1/301

