Optics and Photonics Journal
Vol.2 No.2(2012), Article ID:20400,7 pages DOI:10.4236/opj.2012.22013
Intensity Dependent Nonlinear Absorption in Direct and Indirect Band Gap Crystals under Nano and Picosecond Z-Scan
1Department of Physics, Deenbandhu Chhotu Ram University of Science and Technology (D.C.R.U.S.T), Sonipat, India
2Laser Systems Engineering Division (L.S.E.D.), Raja Rammanna Centre for Advanced Technology (CAT), Indore, India
3Department of Physics, Hindu P.G. College, Sonipat, India
Email: *garun_1965@yahoo.co.in
Received April 12, 2012; revised May 11, 2012; accepted May 25, 2012
Keywords: Direct and Indirect Band Gap Crystals; Two Photon Absorption; Three Photon Absorption; Saturated Absorption
ABSTRACT
The nonlinear absorption properties of direct (GaN) and indirect (CdI2) band gap crystals have been studied by using an open aperture Z-scan technique under fundamental (1064 nm) and frequency doubled (532 nm) wavelength respectively with 10 ns or 60 ps pulse durations. Direct band gap crystal exhibits two and three photon absorption at all input irradiances. On the other hand, at low input irradiance the indirect band gap crystal exhibits saturable absorption (SA). At higher input irradiances two and three photon absorption becomes dominant. A monotonic increase of the nonlinear absorption coefficients with increasing laser pulse duration from 60 ps to 10 ns is observed for GaN and CdI2 crystals.
1. Introduction
Nonlinear optical (NLO) materials play a major role in nonlinear optics and in particular they have a great impact on information technology and industrial applications. In the last decade, however, this effort has also brought its fruits in applied aspects of nonlinear optics. This can be essentially traced to the improvement of the performances of the NLO materials. The aim is to develop materials presenting large nonlinearity and satisfying at the same time all the technological requirements for applications such as wide transparency range, fast response, and high damage threshold.
Direct band gap semiconductors Gallium Nitrate (GaN) with wurtzite crystal structure have a band gap 3.39 ev. The wide band gap of GaN enables this crystal to exhibits special properties for applications in optoelectronics and high power and high frequency devices. On the other hand, many fundamental physical parameters of GaN are still scarcely investigated. Nonlinear optical processes in GaN, such as two and three photon absorption, can lead to optical power limitations and optical damage in nitride based optoelectronics. These processes can be also used in numerous applications: optical limiters, photonic switches and nonlinear autocorrelation systems for ultrafast laser pulse characterization because of these potential applications extensive research efforts have been made on the properties of GaN.
Further cadmium iodide (CdI2) with band gap 3.2 ev is a wide indirect band gap semiconducting material. The optical properties have attracted much attention during the last few years due to its applications as a semiconductor materials detector which may be used in a photo cell or as an x-ray and 𝛾-ray detector. Ultra fast devices are the key component for the next generation. In this case the wide direct and indirect band gap semiconductor is the suitable candidates to calculate the nonlinear absorption parameters. The Z-scan method has been employed to measure the nonlinear optical parameters in number of direct band gap crystals [1-7]. Further there is a lack of measurements on nonlinear parameters in case of indirect band gap crystals because the lattice vibrations and carrier concentration makes the calculations more difficult.
In this paper, we report a systematical investigation on the nonlinear intensity dependent optical absorption coefficients in GaN (direct band gap) and CdI2 (indirect band gap) crystals using nanosecond and picosecond fundamental and frequency doubled Nd:YAG laser by open aperture Z-scan technique. We observed an increase in the value of nonlinear absorption coefficients with increasing laser pulse duration from 60 ps to 10 ns for both the direct and in direct band gap crystals also we observed a switching from saturable absorption (SA) to two and three photon absorption in CdI2 indirect band gap crystal by increasing input irradiances.
2. Z-Scan Theories on Two and Three Photon Absorbers
Under the condition that the photon energy of laser pulses is less than the band-gap energy (Ephoton < Eg), the multi-photon absorption (MPA) coefficients may be evaluated by conducting Z-scans. By using both thin sample approximation and slowly varying envelope approximation, the wave equation can be separated into two equa tions: one for the nonlinear phase and the other for the irradiance: [8,9]
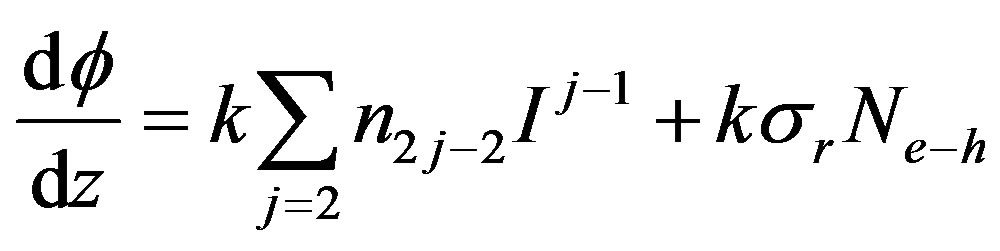 (1)
(1)
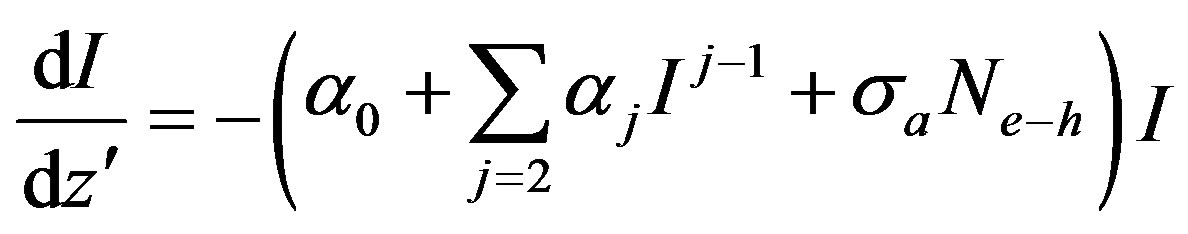 (2)
(2)
where k is the magnitude of the wave vector in free space; n2j–2 is the nonlinear index of refraction (j = 2, 3 for the third and fifth order nonlinearity respectively); σr and σa are the refractive and absorptive cross sections of photoexcited charge carriers (or photo-excited electron-hole pairs), respectively; Ne–h is the number density of the photo-excited charge carriers, α0 is the linear absorption coefficient, αj is the MPA coefficient (j = 2 for 2 PA; j = 3 for 3 PA, and so on); and I is the irradiance within the sample. If we keep the 2 PA term and ignore all other terms on the right side of Equation (2), we can analytically solve Equation (2) for OA Z-scans on two-photon absorbers. Similarly, by keeping the 3 PA term and ignoring the other terms, we can have an analytical expression for OA Z-scans on three-photon absorbers. By assuming a spatially and temporally Gaussian profile for incoming laser pulses, the normalized energy transmittance, TOA(z), for 2 PA and 3 PA can be derived as Equations (3) and (4), respectively [10],
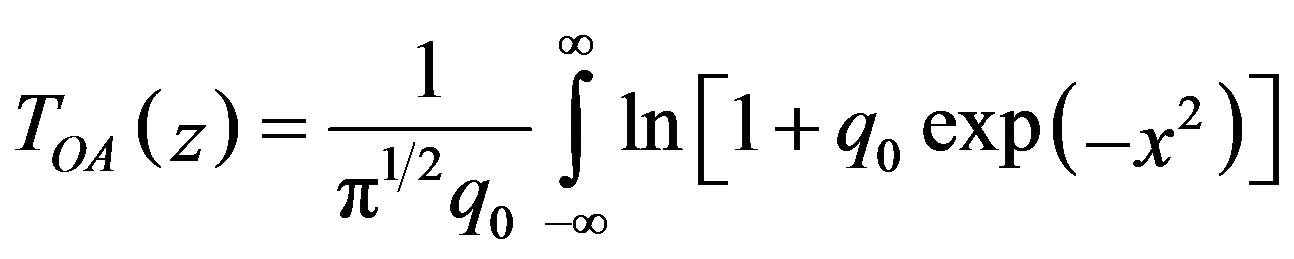 (3)
(3)
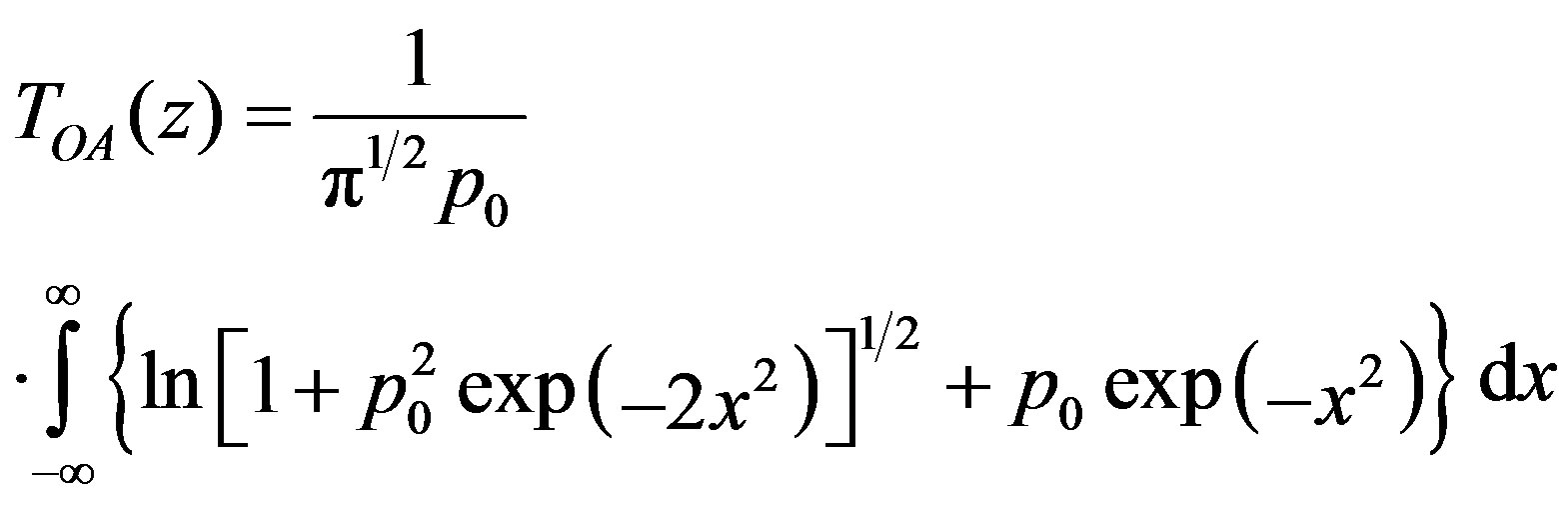 (4)
(4)
where,
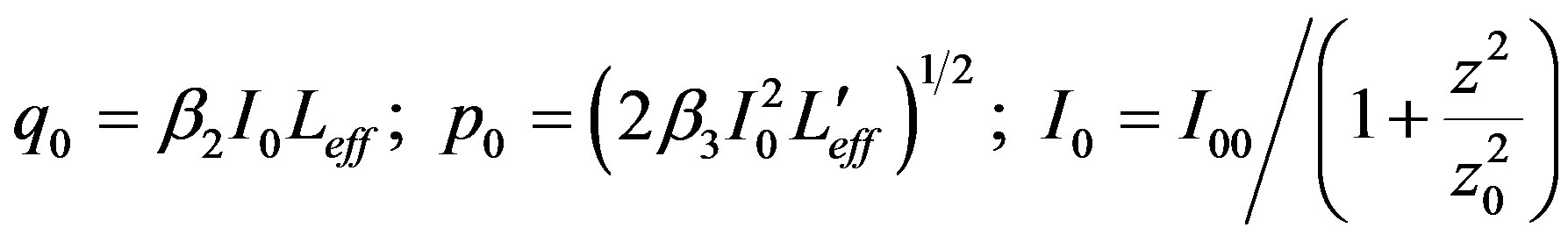 is the excitation intensity at position z;
is the excitation intensity at position z;  is the Rayleigh range; w0 is the minimum beam waist at the focal point; λ is the wavelength of the laser used; Leff =
is the Rayleigh range; w0 is the minimum beam waist at the focal point; λ is the wavelength of the laser used; Leff =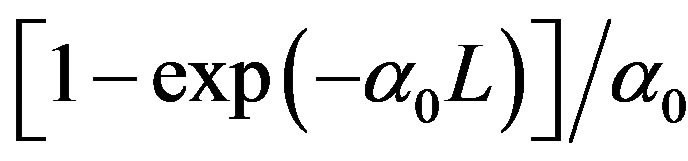 ;
; 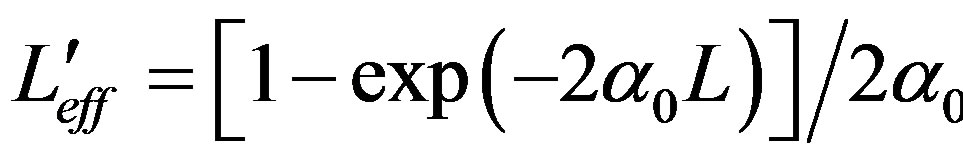 are the effective length of samples for 2 PA and 3 PA processes, respectively; and L is the sample length. The 2 PA and 3 PA coefficients can be extracted by the best fit between the above equations and the OA Z-scan curve at different intensities, as shown in Figures 1-4 respectively.
are the effective length of samples for 2 PA and 3 PA processes, respectively; and L is the sample length. The 2 PA and 3 PA coefficients can be extracted by the best fit between the above equations and the OA Z-scan curve at different intensities, as shown in Figures 1-4 respectively.
It has been pointed out that 3PA Z-scans are significantly different from 2PA Z-scans [11]. If q0 < 1 or p0 < 1, Equation (3) or (4) can be expanded in a Taylor series as
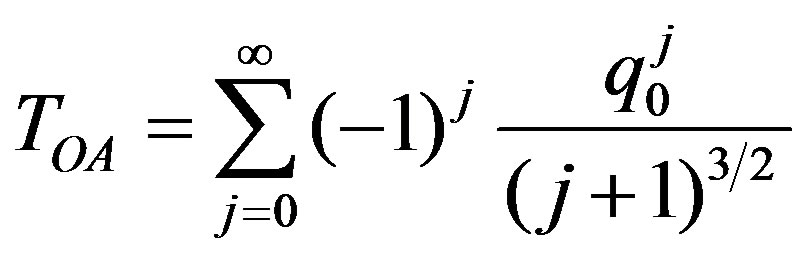 (5)
(5)
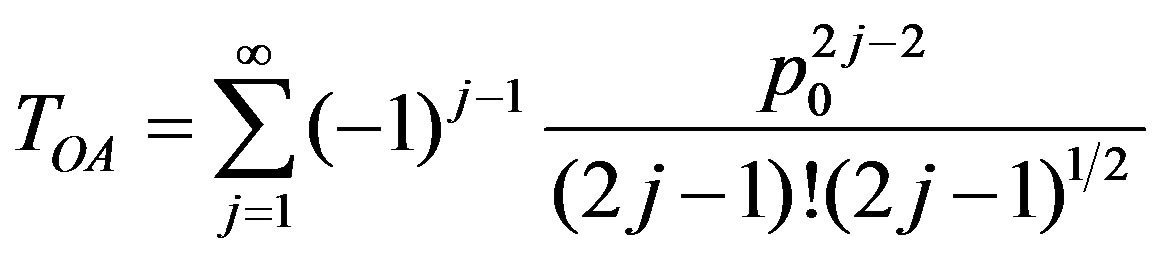 (6)
(6)
Furthermore, if the higher order terms are ignored, we obtain:
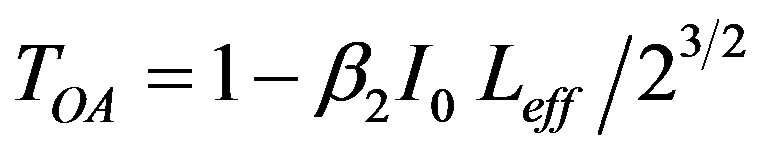 (7)
(7)
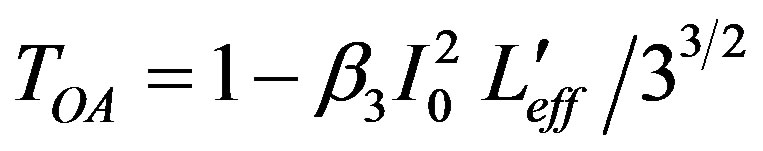 (8)
(8)
By the use of the plot of Ln(1 – TOA) vs Ln(I0) as shown in Figure 5 indicative of 2PA process showing slope 1.86 and 1.92 in case of GaN and CdI2 crystals respectively. Similarly in Figure 6, the plot of Ln(1 – TOA) vs Ln( ) showing slope of 2.9 and 3.0 indicative of 3 PA process in case of GaN and CdI2 crystals respectively.
) showing slope of 2.9 and 3.0 indicative of 3 PA process in case of GaN and CdI2 crystals respectively.
3. Experimental Details
To obtain the nonlinear absorption properties of the samples, the open aperture Z-scan technique shown in Figure 7 has been employed because of its characteristics advantages: simplicity, high sensitivity and simultaneous determinations of both sign and magnitude of the absorptive nonlinearity [12]. In open aperture Z-scan experiments, an optical thin sample moves along the Z-axis near the focal point of the laser beam and the transmitted pulse energy was completely probed as a function of the sample position z and collected with the help of photodiodes. The data only reflect the information on the absorptive nonlinearity because the open aperture Z-scan experiments are insensitive to nonlinear refraction effects such as self phase modulation and harmonic generation [13]. In our experiments the source is fundamental (1.17 eV) and frequency doubled (2.34 ev) Nd:YAG laser produces 10 nsec and 60 psec pulses at 10 Hz repetition rates. All Z-scan measurements reported here at room temperature and radiation for both nanosecond and picoseconds Z-scan experiments was focused by 200 mm
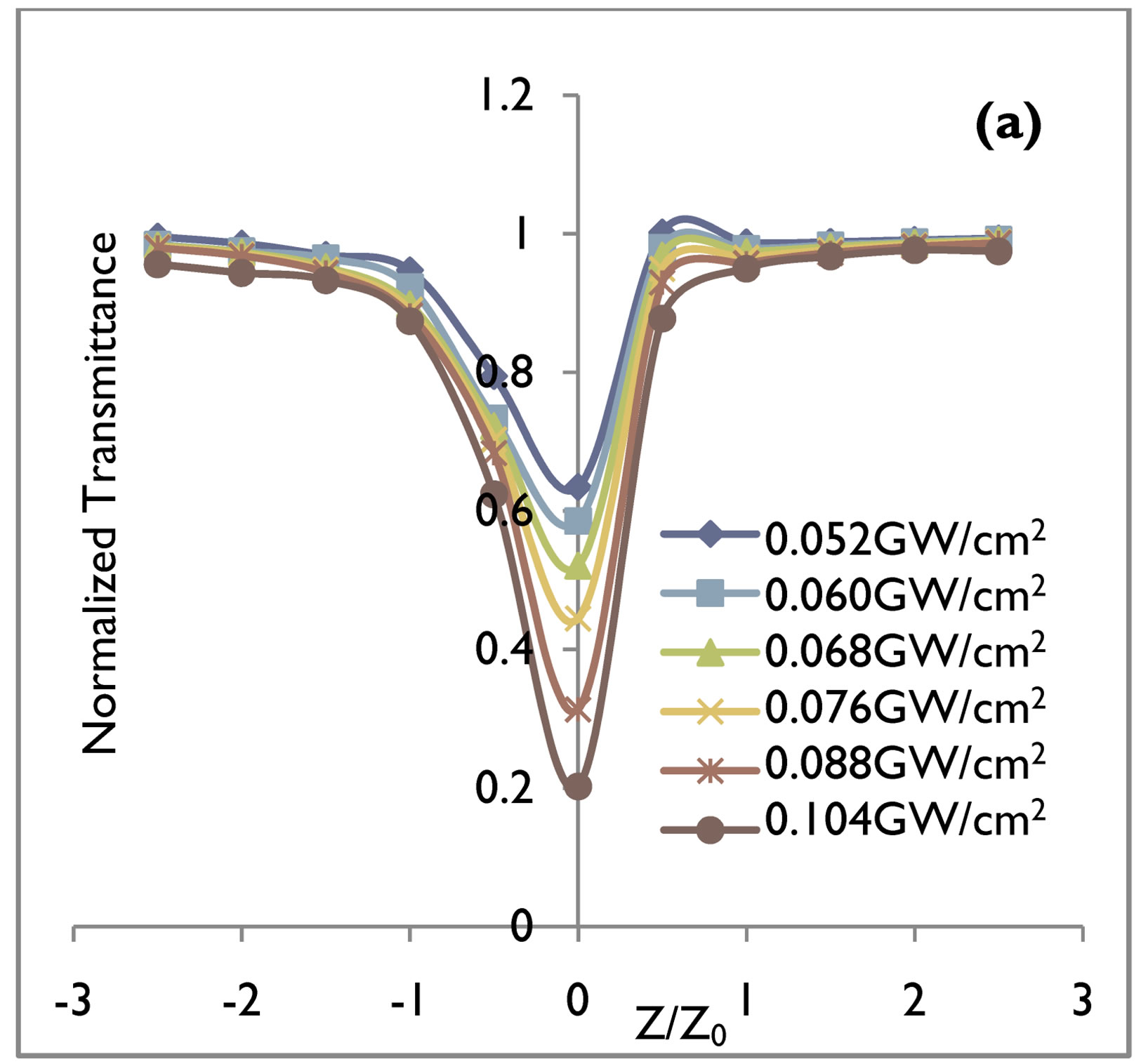
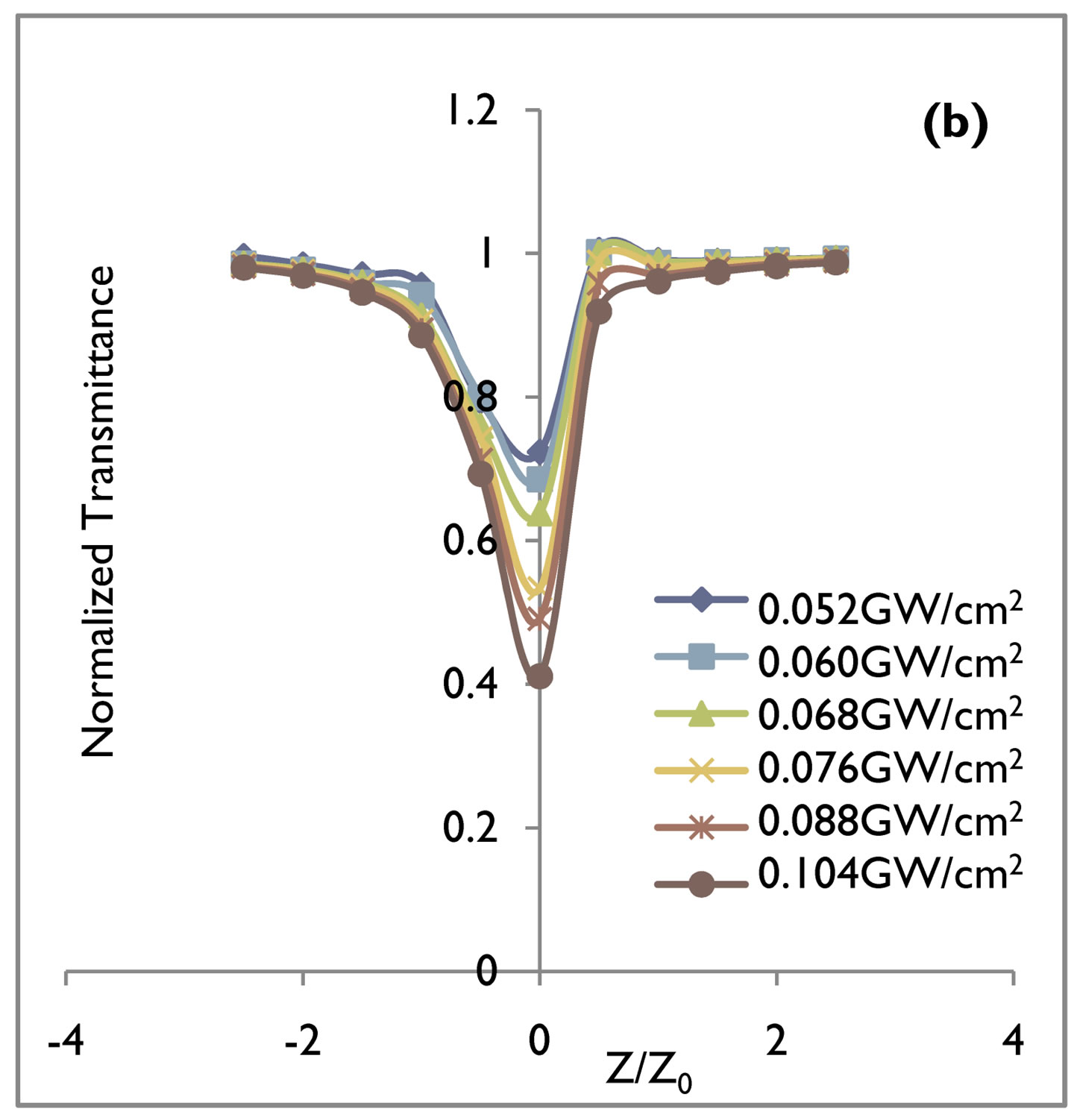
Figure 1. Relative transmittance at 532 nm wavelength for (a) 10 nsec and (b) 60 psec pulse duration of the GaN crystal. Solid line is a theoretical fit to experimental data.
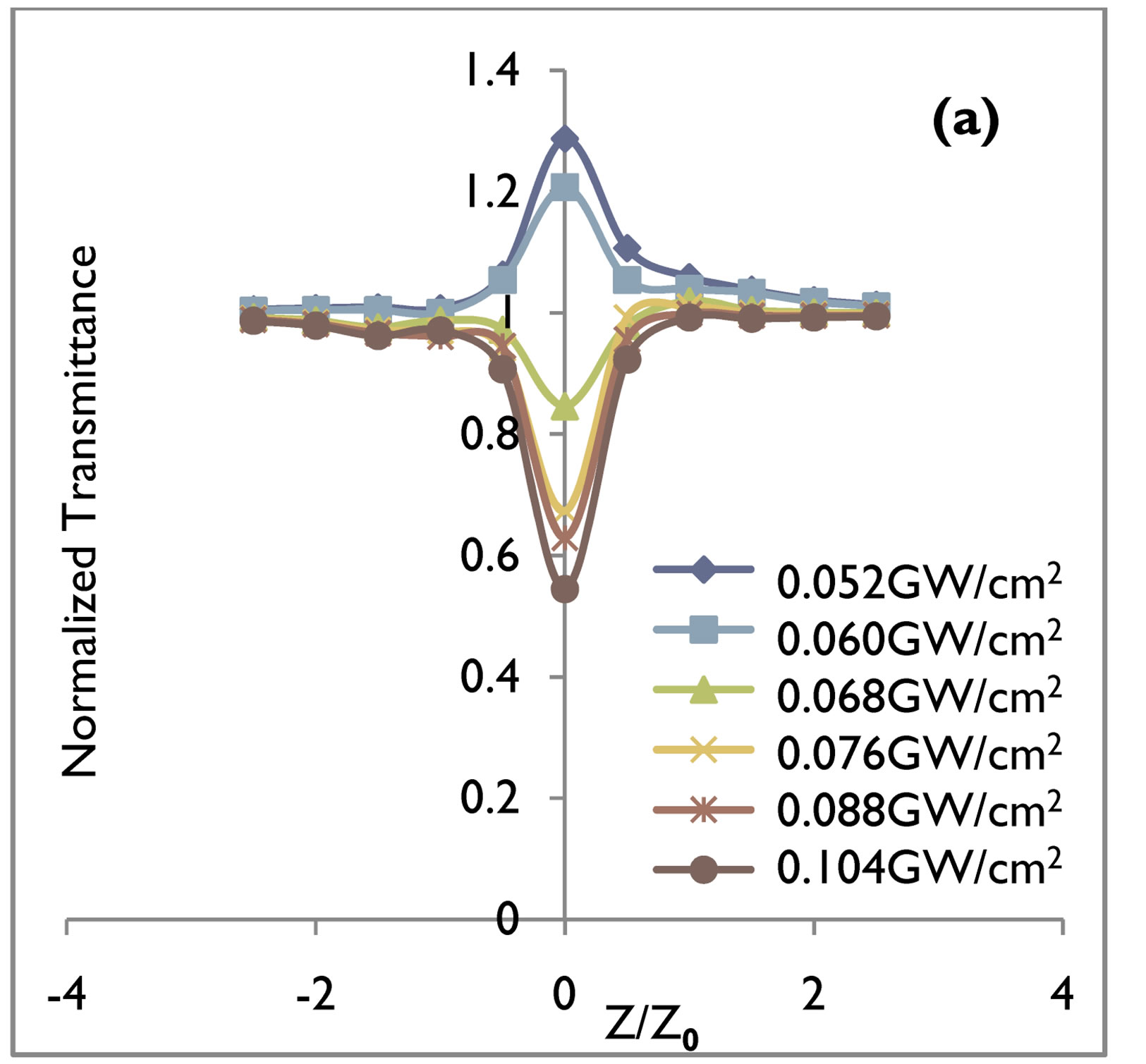
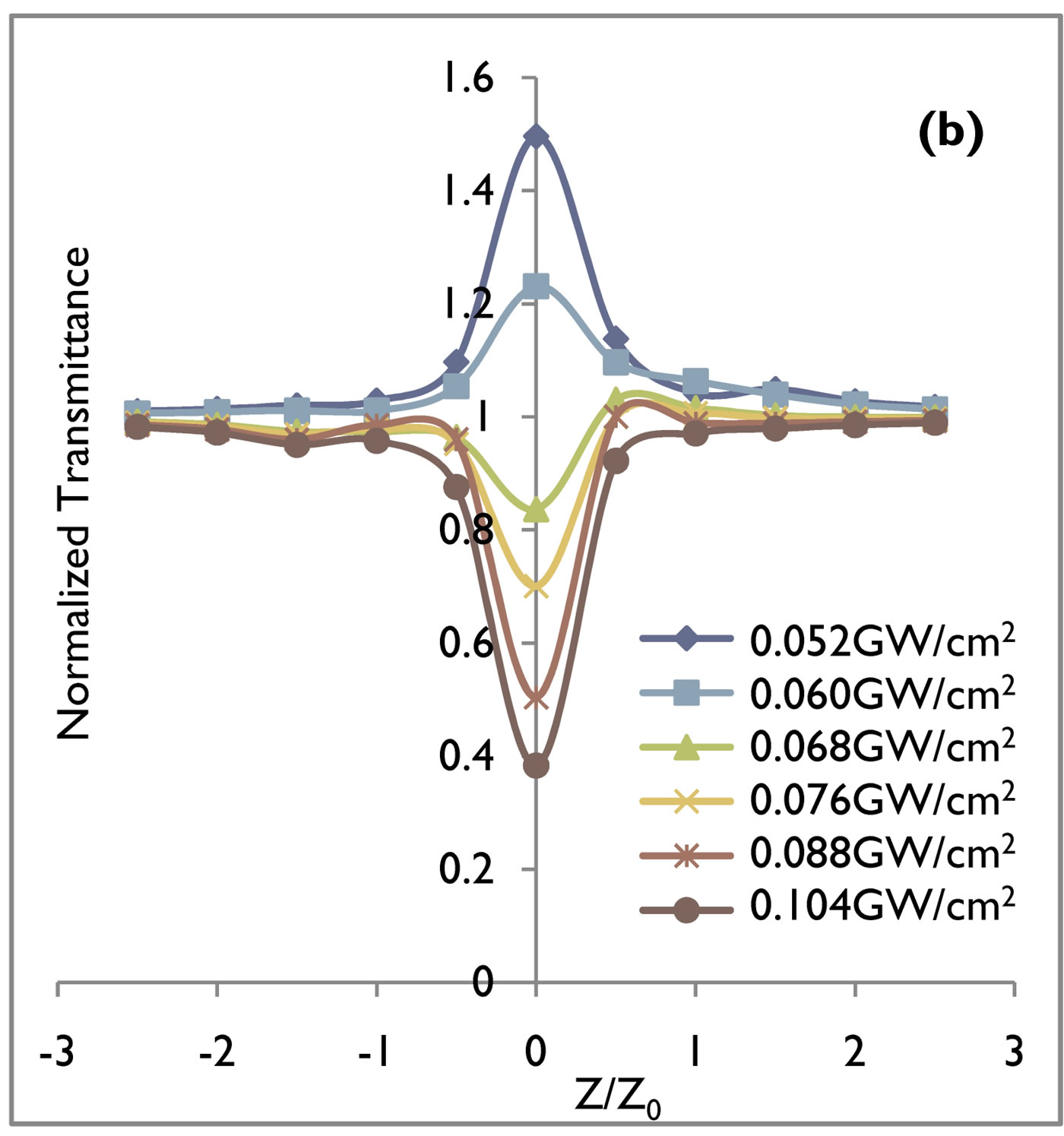
Figure 2. Relative transmittance at 532 nm wavelength for (a) 10 nsec and (b) 60 psec pulse duration of the CdI2 crystal. Solid line is a theoretical fit to experimental data.
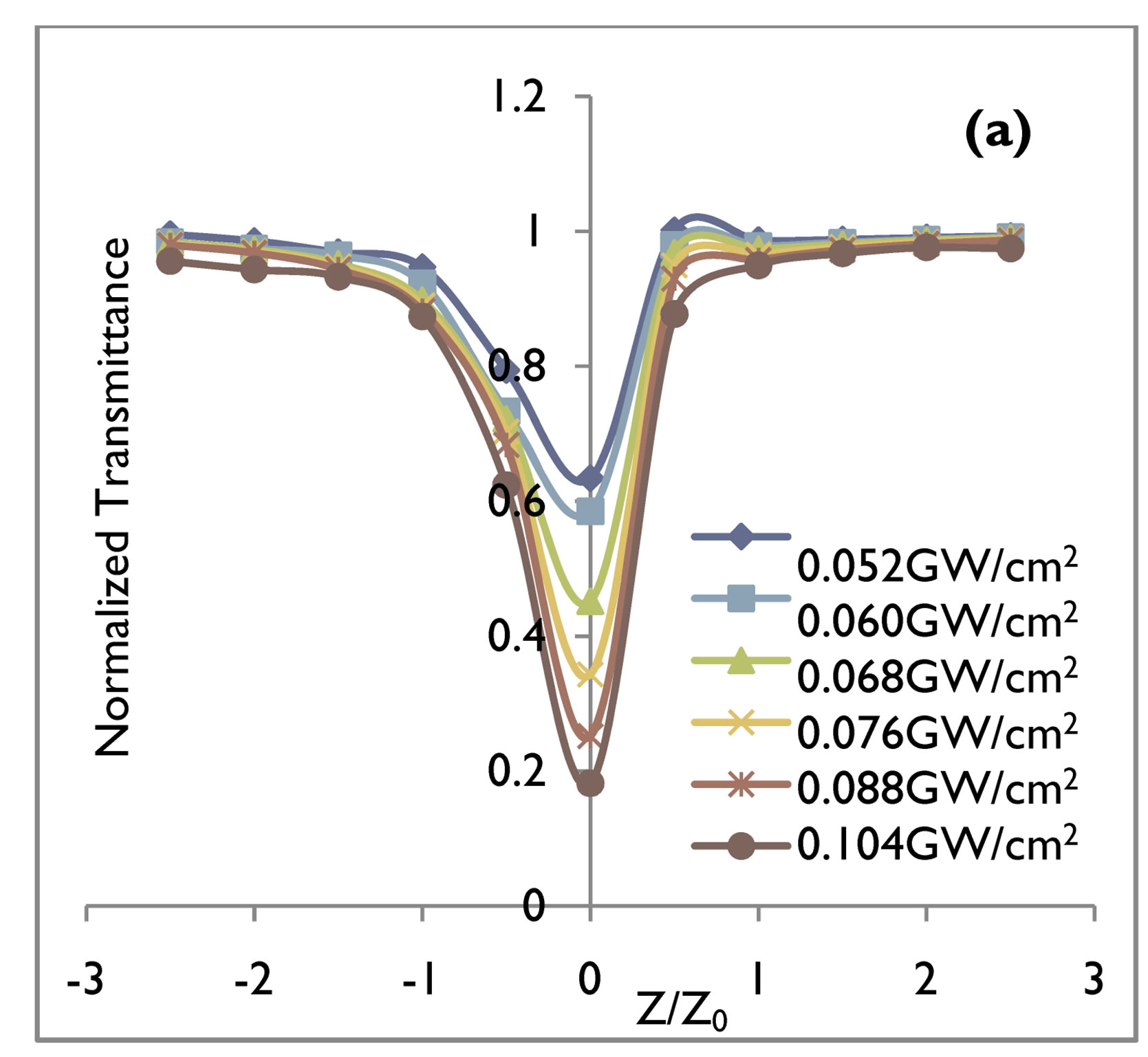
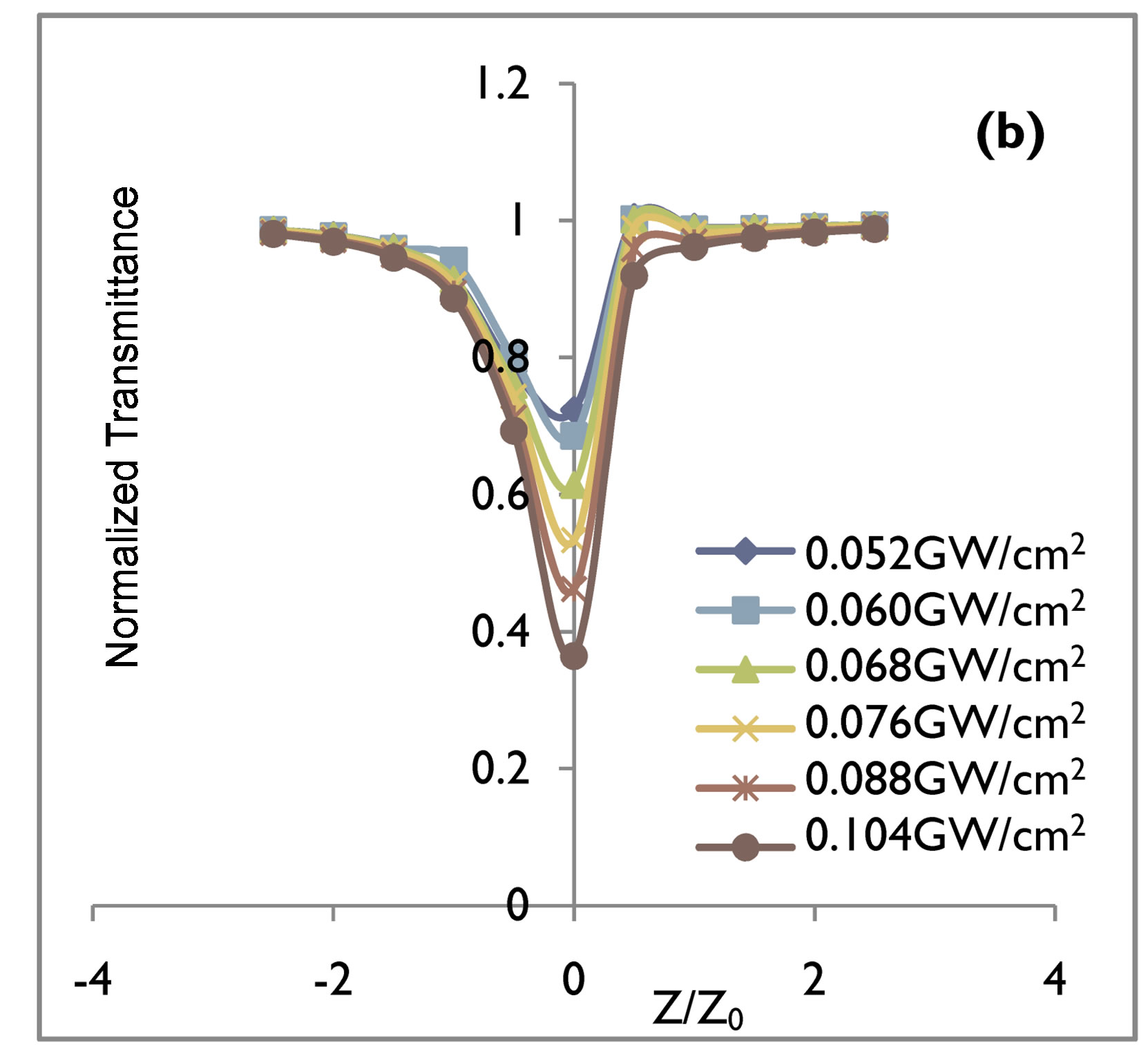
Figure 3. Relative transmittance at 1064 nm wavelength for (a) 10 nsec and (b) 60 psec pulse duration of the GaN crystal. Solid line is a theoretical fit to experimental data.
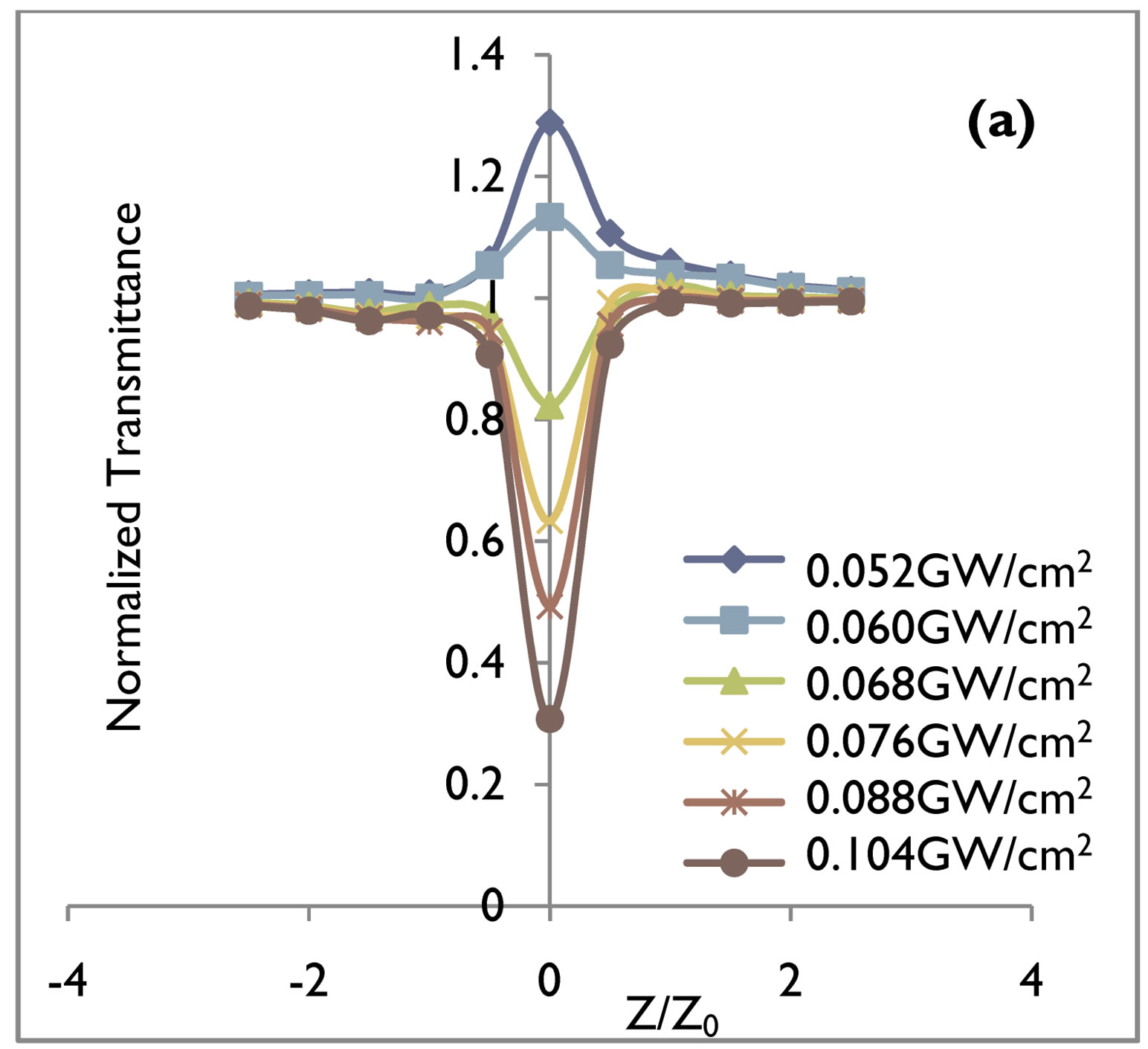

Figure 4. Relative transmittance at 1064 nm wavelength for (a) 10 nsec and (b) 60 psec pulse duration of the CdI2 crystal. Solid line is a theoretical fit to experimental data.
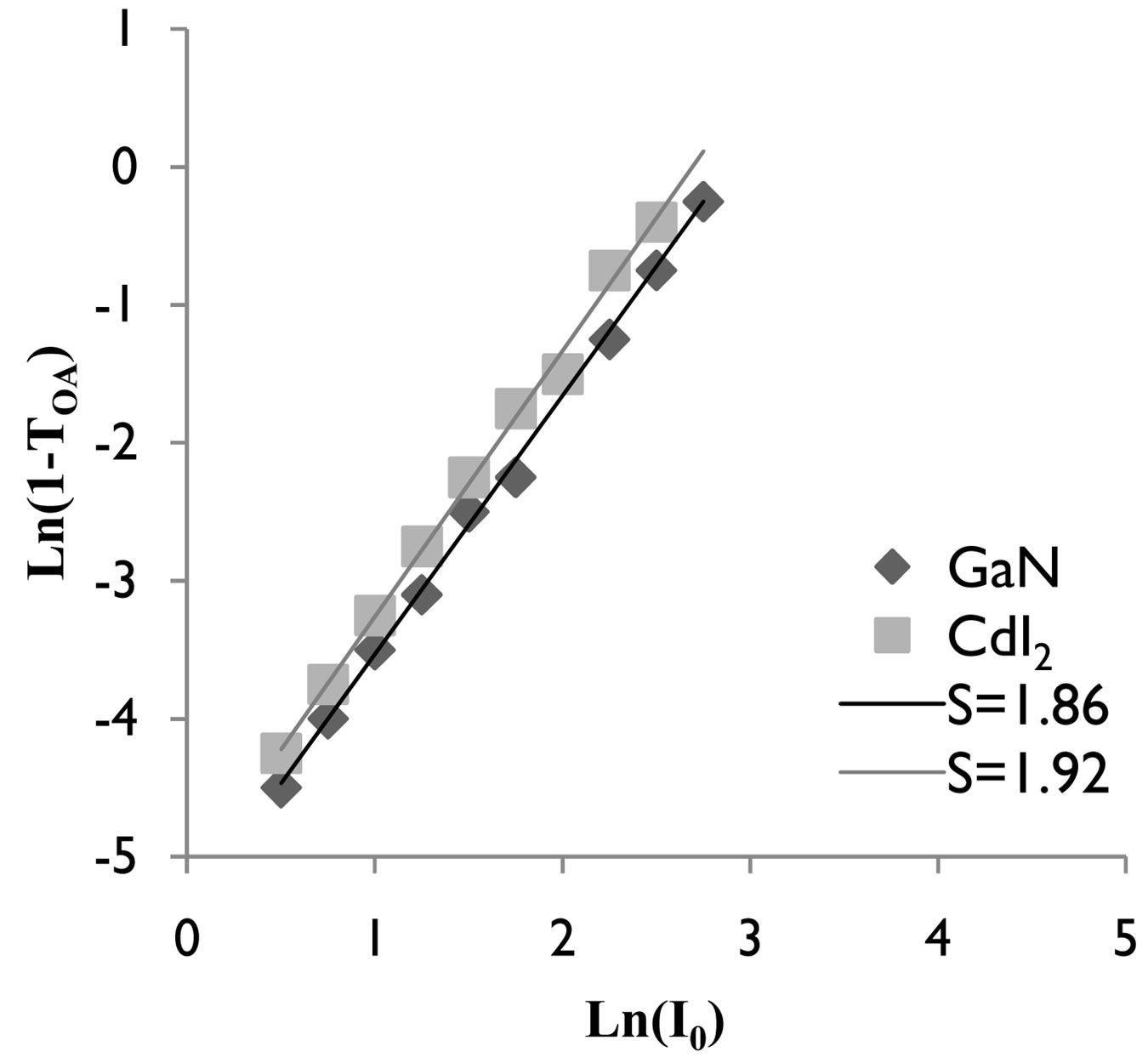
Figure 5. Plot of Ln(1 – TOA) vs Ln(I0) showing 2 PA in case of GaN and CdI2 crystals having slope of a) 1.86 b) 1.92 respectively.
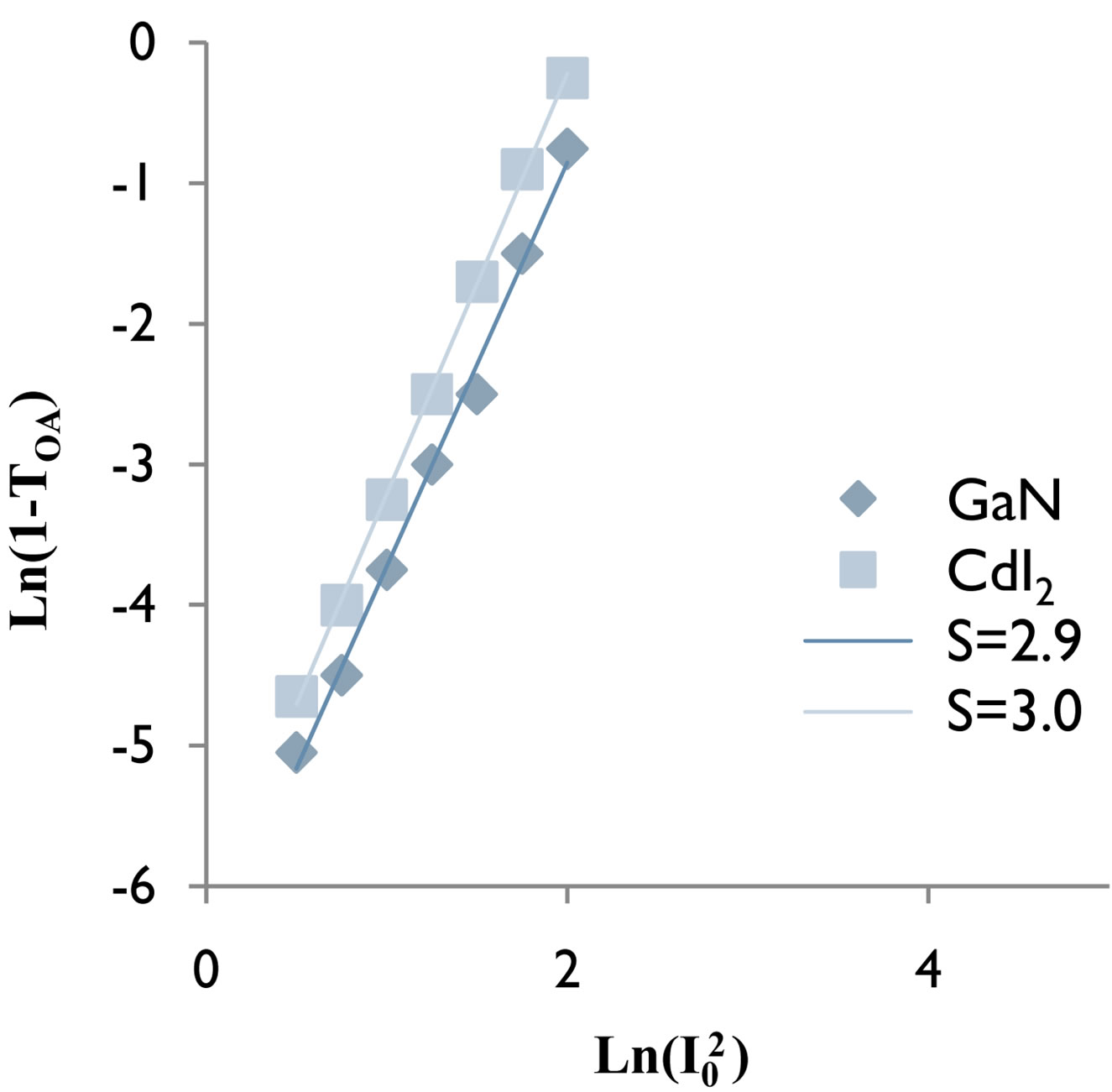
Figure 6. Plot of Ln(1 – TOA) vs Ln(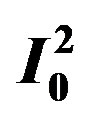 ) showing 3 PA in case of GaN and CdI2 crystals having slope of (a) 2.9 (b) 3.0 respectively.
) showing 3 PA in case of GaN and CdI2 crystals having slope of (a) 2.9 (b) 3.0 respectively.
focal length lens. The Rayleigh length was measured to be 24.4 μm and the Rayleigh length was found to satisfy the basic criteria of Z-scan experiment.
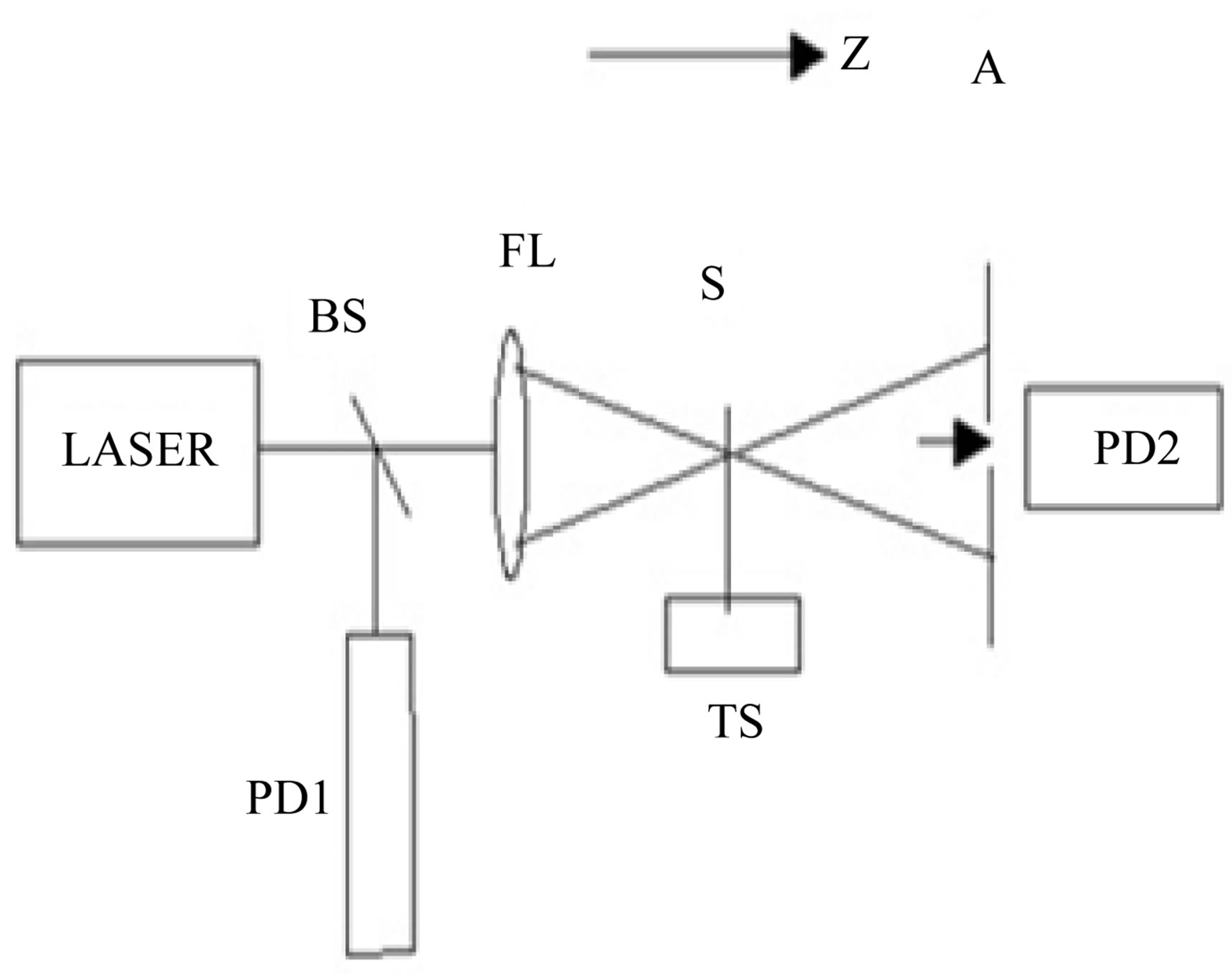
Figure 7. Schematic diagram of experimental Z-scan arrangement. BS beam splitter, FL focusing Lens, S investigated sample, TS translation stage, PD1 and PD2 photodiodes, A aperture.
4. Result and Discussion
Nanosecond and picoseconds open aperture Z-scan measurements show similar behavior for both GaN (direct band gap) and CdI2 (indirect band gap) crystals. Normalised transmittance results of the open aperture Z-scan for an irradiation wavelength of 532 nm of energy 2.34 ev indicating two photon absorption (2 PA) with 10 nsec and 60 psec pulse duration, in case of GaN and CdI2 crystals are shown in Figures 1 and 2 and for wavelength of 1064 nm of energy 1.17 ev indicating three photon absorption (3 PA) with 10 nsec and 60 psec pulse duration in case of GaN and CdI2 crystals are shown in Figures 3 and 4 respectively.
Nonlinear absorption can be classified into two types: first, transmittance increases with increasing optical intensity; this nonlinear absorption corresponds to SA. Second, transmittance reduces with increasing optical intensity, this nonlinear absorption includes two and three photon absorption. In the presence of SA, the intensity dependent absorption coefficient, α(I) is given by
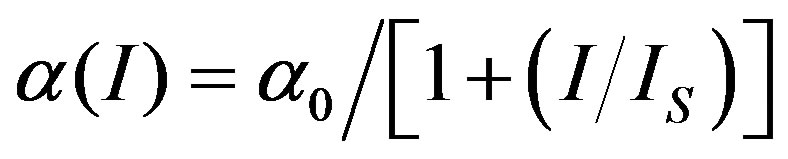 (9)
(9)
where, Is is the saturation intensity. If the excitation intensity I is less than Is, SA can be considered as a third-order process and in such cases –α0/Is is equivalent to two and three photon absorption [14].
The values of the 2 PA and 3 PA coefficients for nanosecond and picosecond pulse duration at 0.052 cm/GW2 to 0.104 cm/GW2 input intensities with theoretical fit are given in Tables 1 and 2 for both the direct and indirect band gap crystals. The value of 2 PA and 3 PA coefficients in case of indirect band gap crystals in both the nanosecond and picosecond regime’s are smaller as compared to direct band gap crystals. This fact can be easily be understood as reported earlier [15] due to phonon assisted transition in case of indirect band gap crystals. With increasing input irradiances the 2 PA and 3 PA coefficients of GaN and CdI2 crystals increases in magnitude for nanosecond and picosecond pulse duration. The indirect band gap crystal exhibited a switching from saturated absorption to two and three photon absorption by increasing input intensities. It is found that in general, they exhibit either saturated absorption or 2 PA and 3 PA depending on the intensity of the excitation. For 0.052 cm/GW2 and 0.060 cm/GW2 input intensities, the dominant nonlinear absorption is saturated while for 0.068 cm/GW2 to 0.104 cm/GW2 2 PA and 3 PA is dominant. Saturable absorption characteristics depend on the properties of a materials and the parameters such as intensity and pulse duration of laser used [16-18]. It is well known that when the photon energy h𝜈 is less than the band gap Eg, 2 PA and 3 PA processes are dominant mechanisms as observed in semiconducting materials [19-21]. At low input irradiance, Figures 2 and 4 in case of indirect band gap crystals in our open aperture Z-scan measurements, the 532 nm and 1064 nm laser radiation yielding SA. SA is dominant at low input irradiance, although 2 PA and 3 PA always exist. However, at higher input irradiance, the absorption from the free carriers becomes significant and 2 PA and 3 PA becomes dominant. The intensity dependence SA, 2 PA and 3 PA at the same wavelength in the crystals may be used for optical pulse compression [22]. Results in Tables 1 and 2 for both direct and indirect band gap crystals show that β2 and β3 values for nanosecond pulse duration at the same input irradiance are about one order of magnitude larger than β2 and β3 values for picosecond pulse duration. It is known that the third order nonlinearities arising from bound electronic effects are important in the femtosecond time region, while the free carrier nonlinearities become significant for laser pulses of nanosecond durations and larger.
It was found previously that free carrier generation
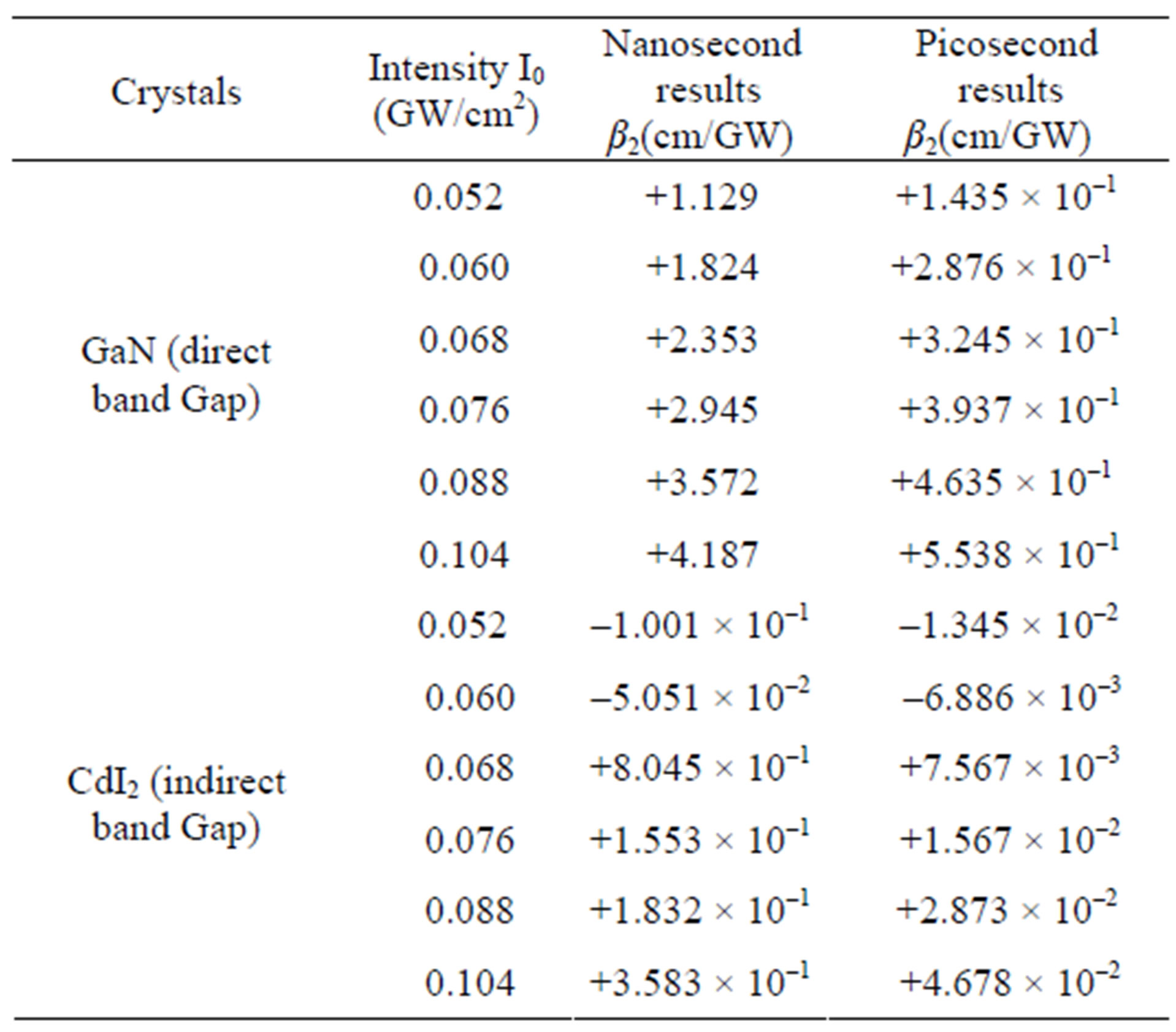
Table 1. Comparison of the nonlinear two photon absorption coefficients of the GaN (direct band gap) and CdI2 (indirect band gap) crystals, for nanosecond and picoseconds (l = 532 nm) laser excitation at various input intensities.
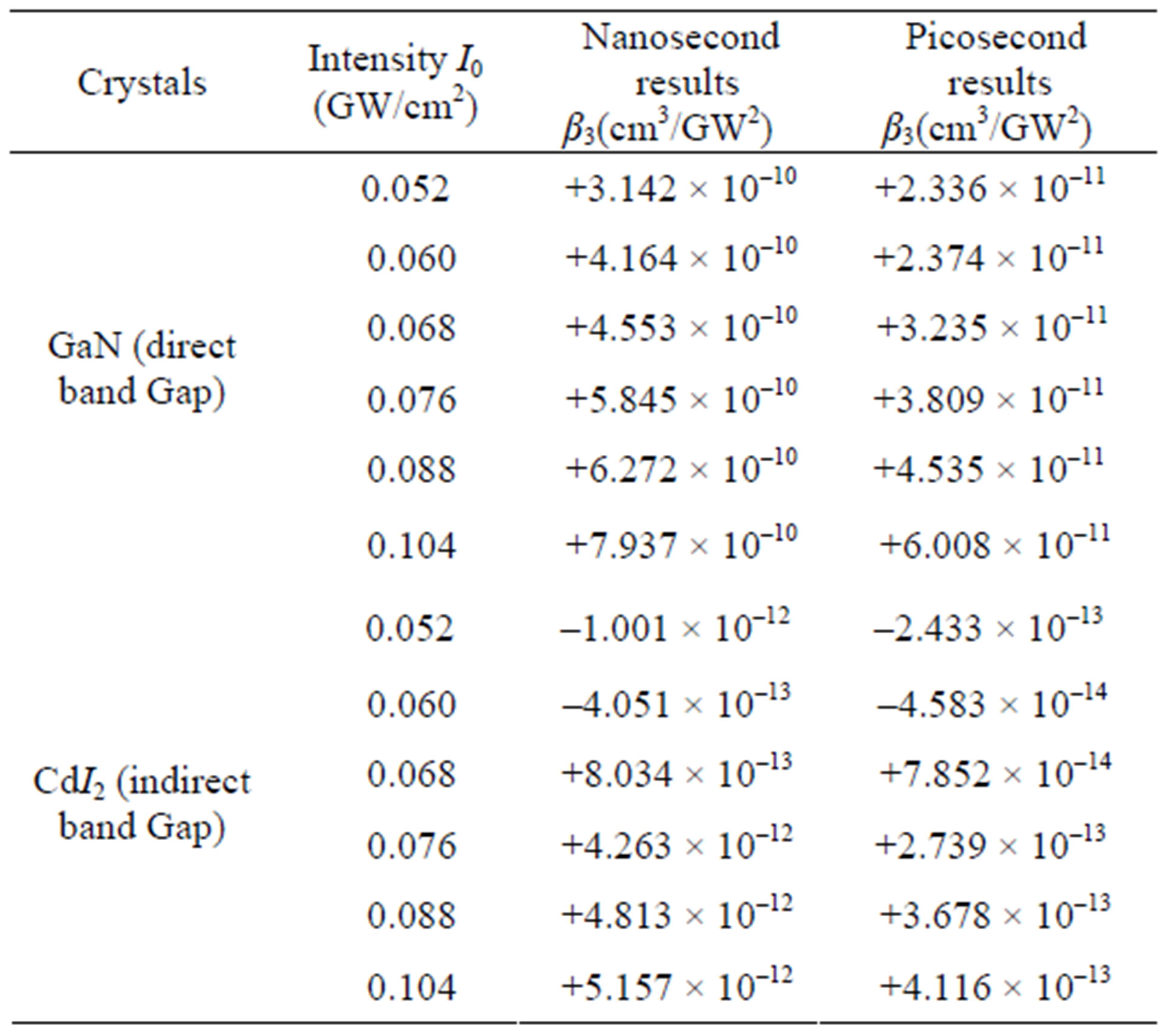
Table 2. Comparison of the nonlinear three photon absorption coefficients of the GaN (direct band gap) and CdI2 (indirect band gap) crystals, for nanosecond and picoseconds (l = 1064 nm) laser excitation at various input intensities.
under high laser intensities in the picosecond time regime should be included in the consideration of nonlinear optics in semiconductors [23]. Longer pulses can make nonlinear absorption processes such as two and three photon induced free carrier absorption dominant. If pulses have the same peak intensity with different temporal width are incident on a materials, longer pulses will create more carriers, thus the longer pulse will include more free carrier absorption with small carrier decay times [22]. For example, electron-hole recombination times for CdS and ZnSe were found to be of the order of 0.6 - 4.0 ns [23-27] and the contribution of free carriers to thirdorder nonlinearities was found to be significant for laser pulses of nanosecond duration. In our Z-scan experiments, the same low intensity value (0.052 GW/cm2) was used for both 60 psec and 10 nsec pulse durations. Therefore, the results in Tables 1 and 2 indicate that the free charge carrier contributions to the third order nonlinearities in the nanosecond Z-scan experiments are much larger than that of picosecond Z-scan experiments.
5. Conclusion
The nonlinear absorption of GaN (direct band gap) and CdI2 (indirect band gap) crystals have been calculated by the open aperture Z-scan technique under 532 nm and 1064 nm wavelength with 10 nsec and 60 psec pulse duration. Smaller values of two and three photon absorption coefficients in case of indirect band gap crystals as compared to direct band gap crystals have been attributed to phonon assisted transition. Direct band gap crystals exhibited two and three photon absorption while indirect band gap crystal exhibited a switching from negative nonlinear absorption (saturated absorption) to positive nonlinear absorption (two photon and three photon absorption) by increasing input irradiances. The saturable is dominant at low input irradiance in case of indirect band gap crystal while two and three photon absorption is dominant for high input irradiances. The intensity dependent saturable absorption, two and three photon absorption in the indirect band gap CdI2 crystal may be used for optical pulse compression.
6. Acknowledgements
Authors are thankful to Ms. Meenu Rani, Rajeev Vats and Dr. Raj Kumar Sharma for their helpful discussion.
REFERENCES
- M. S. Bahae, D. C. Hutchings, D. J. Hagan and E. W. Van Stryland, “Dispersion of Bound Electronic Nonlinear Refraction in Solids,” IEEE Journal of Quantum Electron, Vol. 27, No. 6, 1991, pp. 1296-1309. doi:10.1109/3.889946
- A. A. Said, M. Sheikh-Bahae, D. J. Hagan, T. H. Wei, J. Wang, J. Young and E. W. Van Stryland, “Determination of Bound Electronic and Free Carrier Nonlinearities in ZnSe, GaAs, CdTe and ZnTe,” Journal of Optical Society of America B, Vol. 9, No. 3, 1992, pp. 405-414. doi:10.1364/JOSAB.9.000405
- T. D. Krauss and F. W. Wise, “Femtosecond Measurement of Nonlinear Absorption and Refraction in CdS, ZnSe, ZnS,” Applied Physics Letter, Vol. 65, No. 14, 1994, pp. 1739-1741. doi:10.1063/1.112901
- D. C. Hucthing and B. S. Wherrett, “Theory of the Anisotropy of Ultrafast Nonlinear Refraction in Zinc-Blende Semiconductors,” Physics Revolution B, Vol. 52, No. 11, 1995, pp. 8150-8159.
- V. Pacebutas, A. Kratkus, T. Suski, P. Perlin and M. Leszczynski, “Photoconductive Z-Scan Measurement of Multiphoton Absorption of GaN,” Journal of Applied Physics, Vol. 92, No. 11, 2002, pp. 6930-6932.
- R. A. Ganeev, M. Baba, M. Morita, D. Rao, H. Fujii, A. I. Rayasnyansky, N. Ishizawa, M. Suzuki and H. Kuroda, “Nonlinear Optical Properties of CdS and ZnS Nanoparticles Doped into Zirconium Oxide Films,” Journal of Optics A: Pure and Applied Optics, Vol. 6, No. 4, 2004, pp. 447-453. doi:10.1088/1464-4258/6/4/024
- A. Gaur, D. K. Sharma, D. S. Ahlawat and N. Singh, “Multiphoton Photoconductivity and Optical Nonlinearities in ZnSe and CdSe Direct Band Gap Crystals,” Journal of Optics A: Pure and Applied Optics, Vol. 9, No. 3, 2007, pp. 260-264. doi:10.1088/1464-4258/9/3/009
- E. W. Van Stryland, H. Vanherzeele, M. A. Woodall, M. J. Soileau, A. L. Smirl, S. Guha and T. F. Boggess, “Two Photon Absorption, Nonlinear Refraction and Optical Limiting in Semiconductors,” Optical Engineering, Vol. 24, No. 4, 1985, pp. 613-623.
- J. H. Bechtel and W. L. Smith, “Two Photon Absorption in Semiconductors with Picoseconds Laser Pulses,” Physics Revolution B, Vol. 13, No. 8, 1976, pp. 3515-3522. doi:10.1103/PhyRevB.13.3515
- R. L. Sutherland, D. G. McLean and S. Kirkpatrick, “Handbook of Nonlinear Optics,” 2nd Edition, Marcel Dekker, New York, 2003.
- K. S. Bindra, H. T. Bookey, A. K. Kar, B. S. Wherrett, X. Liu and A. Jha, “Nonlinear Optical Properties of Chalcogenide Glasses: Observation of Multiphoton Absorption,” Applied Physics Letter, Vol. 79, No. 13, 2001, pp. 1939- 1941. doi:10.1063/1.1402158
- M. S. Bahae, A. A. Said, T.-H. Wei, D. J. Hagan and E. W. Van Stryland, “Sensitive Measurement of Optical Nonlinearities Using a Single Beam,” IEEE Journal of Quantum Electron, Vol. 26, No. 4, 1990, pp. 760-769. doi:10.1109/3.53394
- T. Tritschler, O. D. Mucke, M. Wegener, U. Morgner and F. X. Kartner, “Evidence for Third Harmonic Generation in Disguise of Second-Harmonic Generation in Extreme Nonlinear Optics,” Physics Revolution Letter, Vol. 90, No. 21, 2003, pp. 217404-217408. doi:10.1103/PhyRevLett.90.217404
- L. Irimpan, A. Deepthy, B. Krishnan, L. M. Kukreja, V. P. N. Nampoori and P. Radhakrishnan, “Effect of Self Assembly on the Nonlinear Optical Characteristics of ZnO Thin Films,” Optics Communication, Vol. 281, No. 10, 2008, pp. 2938-2943. doi:10.1016/j.optcom.2008.01.029
- D. S. Ahlawat, A. Gaur, N. Singh and R. D. Singh, “Pulsed Laser Induced Multiphoton Photoconductivity in an Indirect Band Gap Crystal: PbI2,” Physica Statistica Solidi (b), Vol. 219, 2000, pp. 421-424.
- A. M. Kulibekov, K. Allakhverdiev, D. A. Guseinova, E. Y. Salaev and O. Baran, “Optical Absorption in GaSe under High Density Ultra Short Pulses,” Optics Communication, Vol. 239, No. 1-3, 2004. pp. 193-198. doi:10.1016/j.optcom.2004.05.011
- R. Philip, G. R. Kumar, N. Sandhyarani and T. Pradeep, “Picosecond Optical Nonlinearity in Monolayered-Protected Gold, Silver, and Gold-Silver Alloy Nanoclusters,” Physics Revolution B, Vol. 62, No. 19, 2000, pp. 13160- 13166. doi:10.1103/PhyRevB.62.13160
- U. Gurudas, E. Brooks, D. M. Bubb, S. Heiroth, T. Lippert and A. Wokaun, “Pd Nanoparticles Formation by Femtosecond Laser Irradiation and the Nonlinear Optical Properties at 532 nm Using Nanosecond Laser Pulses,” Journal of Applied Physics, Vol. 104, No. 7, 2008, pp. 073107-073115. doi:10.1063/1.2990056
- K. L. Vodopyanov, S. B. Mirov, V. G. Voevodin and P. G. Schunemann, “Two Photon Absorption in GaSe and CdGeAs2,” Optics Communications, Vol. 155, No. 1-3, 1998, pp. 47-51. doi:10.1016/S0030-4018(98)00364-2
- K. R. Allakhverdiev, T. Baykara, S. Joosten, E. Gunay, A. A. Kaya, A. Kulibekov, A. Seilmeier and E. Y. Salaev, “Anisotropy of Two Photon Absorption in Gallium Selenide at 1064 nm,” Optics Communications, Vol. 261, No. 1, 2006, pp. 60-64. doi:10.1016/j.optcom.2005.11.046
- F. Adduci, I. M. Catalano, A. Cingolani and A. Minafra, “Direct and Indirect Two Photon Processes in Layered Semiconductors,” Physics Revolution B, Vol. 15, No. 2, 1977, pp. 926-931. doi:10.1103/PhyRevB.15.926
- Y. B. Band, D. J. Harter and R. Bavli, “Optical Pulse Compressor Composed of Saturable and Reverse Saturable Absorbers,” Chemical Physics Letter, Vol. 126, No. 3-4, 1986, pp. 280-284. doi:10.1016/S0009-2614(86)80083-5
- H. P. Li, C. H. Kam, Y. L. Lam and W. Ji, “Optical Nonlinearities and Photo Excited Carrier Life Time in CdS at 532 nm,” Optics Communications, Vol. 190, No. 1-6, 2001, pp. 351-356. doi:10.1016/S0030-4018(01)01066-5
- E. C. Fox and H. M. Van Driel, “Femtosecond Probing of Photoinduced Refractive Index Changes in Semiconductors,” In: W. E. Bron, Ed., Ultrashort Processes in Condensed Matter, Plenum Press, New York, 1993.
- J. Wang, M. Sheik-Bahae, A. A. Said, D. J. Hagan and E. W. Van Stryland, “Time Resolved Z-Scan Measurements of Optical Nonlinearities,” Journal of Optical Society America B, Vol. 11, No. 6, pp. 1009-1017. doi:10.1364/JOSAB.11.001009
- K. Y. Tseng, K. S. Wong and G. K. L. Wong, “Femtosecond Time Resolved Z-Scan Investigations of Optical Nonlinearities in ZnSe,” Optics Letter, Vol. 21, No. 3, 1996, pp. 180-182. doi:10.1364/OL.21.000180
- J. F. Lami and C. Hirlimann, “Two Photon Excited Room Temperature Luminescence of CdS in the Femtosecond Regime,” Physics Revolution B, Vol. 60, No. 7, 1999, pp 4763-4770. doi:10.1103/PhyRevB.60.4763
NOTES
*Corresponding author.

