Journal of Surface Engineered Materials and Advanced Technology
Vol.06 No.04(2016), Article ID:71428,18 pages
10.4236/jsemat.2016.64017
Adsorption of Pharmaceuticals and Personal Care Products on Granular Activated Carbon
Nasly Y. Delgado1,2*, Alberto L. Capparelli2,3, Damián J. Marino1,2, Agustín F. Navarro4, Gustavo A. Peñuela5, Alicia E. Ronco1,2*
1Centro de Investigaciones del Medio Ambiente, Facultad de Ciencias Exactas, Universidad Nacional de la Plata (UNLP), La Plata, Argentina
2Consejo Nacional de Investigaciones Científicas y Técnicas, La Plata, Argentina
3División Fisicoquímica, Facultad de Ciencias Exactas, UNLP, La Plata, Argentina
4Departamento de Ingeniería Química, Facultad de Ingeniería, UNLP, La Plata, Argentina
5Grupo GDCON, Universidad de Antioquia, Medellín, Colombia
Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: September 9, 2016; Accepted: October 21, 2016; Published: October 24, 2016
ABSTRACT
We investigated the adsorption to granular activated carbon of two pharmaceuticals (carbamazepine and sildenafil citrate) and a personal-care product (methylparaben) in aqueous solution, characterized the carbon, and evaluated its influence on the kinetics and adsorption equilibrium of the compounds under study. We adjusted data for the analysis of equilibrium to Langmuir and Freundlich models of adsorption isotherms and described adsorption rate using pseudo first- and second-order models; that same analysis was made on the basis of the behavior of the initial rate. In addition, we analyzed the potentiality of a nonlinear adjustment for studying kinetics and equilibrium of adsorption, an approach requiring neither knowledge of equilibrium conditions nor a-priori hypothetical suppositions regarding the order of reaction. The results indicated that the nonlinear model was capable of describing adsorption kinetic behavior, in order to determine concentrations adsorbed at equilibrium, adsorption rates of the system, maximum adsorption capacity, and global rate constant. Granular carbon exhibited an adsorption capacity for carbamazepine and methylparaben of ca. 323 mg/g and for sildenafil citrate of ca. 142 mg/g, though with slow adsorption kinetics characterized by average adsorption times of at least 168 h.
Keywords:
Activated Carbon, Carbamazepine, Sildenafil Citrate, Methylparaben, Adsorption

1. Introduction
Because of the current habits of consumerism in our society, a succession of contaminants have gone on accumulating in the environment whose presence has managed to escape attention until only a few years ago. These contaminants, referred to as emergent, are compounds of different origins and chemical natures; among which can be cited pesticides, hormones, drugs resulting from abuse, pharmaceuticals, and commercial products for personal hygiene or care [1] - [3] . These contaminants, after their administration or use, become incorporated in aquatic systems through wastewater. Certainly these substances, because of their refractory characteristics, are not removed in the conventional wastewater-treatment plants and thus reach the surface water and the systems of purification [4] [5] . Consequently, at the present time, investigations are being carried out regarding treatment strategies for the removal of such emergent pollutants. These procedures are based on knowledge of the physicochemical properties of such substances and their environmental behavior [6] .
Among those procedures, the technology of adsorption onto activated carbon― owing to its large specific surface, its micropore structure and high adsorption capacity― offers a great potential for its use within the system of treatment for removal of traces of emergent contaminants [7] [8] . The prediction of the speed at which such an adsorption is affected for a given system is probably the most important factor in those systems with designs based on this technology [9] . At the end of the 19th century, Lagergren proposed a model of pseudo first order for determining the rate of adsorption onto activated carbon [10] , a model that is perhaps the oldest and the most frequently used for the study of adsorption kinetics, to which treatment should also be added the model of pseudo second-order kinetics.
Within the information on the adsorption capacity, an understanding of the concentration of adsorbate at equilibrium (qe), the maximum adsorption capacity (qm), the apparent rate constants (k1 or k2), the global rate constant (K), and the coverage fraction are essential in order to have a complete panorama of the adsorption kinetics and equilibrium. In the present investigation, we studied those processes through a nonlinear-regression analysis of the experimental information that obviated the hypothesis of pseudo first- and second-order kinetics, allowing us to resolve certain limitations of the classical models where hypotheses are proposed to consider the type of kinetics describing the system. Thus, the most fundamental parameters of the equations describing the adsorption arise without postulating any previous supposition, as will be discussed in detail below.
In the work reported here, we studied the kinetics and equilibrium of adsorption onto commercial granular activated carbon of three emergent contaminants: methylparaben (Mp), carbamazepine (Cbz), and sildenafil citrate (Sil); those selected as being representative of such pollutants in wastes within the environment [1] [2] . The objective of this investigation was to provide new information in order to gain a better understanding of the parameters and mechanisms involved in the processes of adsorption and to develop a technique for the removal of pharmaceuticals and personal-care products (PPCPs) from urban wastewaters that would be applicable to full scale.
2. Experimental
2.1. Adsorbent and Adsorbates
The commercial granular-activated-carbon mesh-29 used had a surface area of 956 m2/g, a pore size of 20 Å, a mean diameter of 1 mm, and a pore volume of 0.46 cm3/g, as evaluated from Brunauer-Emmett-Teller (BET) measurements. The adsorbates used were two pharmaceuticals, Cbz and Sil, and a personal-care product, Mp, of pharmacopeia quality (Parafarm Drugstore, Saporiti, Argentina). Table 1 lists the physicochemical characteristics of the three compounds. Stock 1000 mg/L solutions were prepared by dissolving the compounds in 99.9% methanol, from which stocks the appropriate volumes were taken and diluted with distilled water for the calibration and adsorption experiments.
2.2. Adsorption Assays
To determine the working mass of carbon to be used, batch experiments were maintained at a constant concentration of 5 mg/L for each separated sample in a fixed volume of 50 mL and varying quantities of activated carbon: 5, 25, 50, 100 and 200 mg,
Table 1. Physicochemical properties of the emergent contaminants selected.
a. Abbreviations used: Cs, chemical structure; CAS, Chemical Abstracts Service registry number; Mw, molar weight; Ws, water solubility; pKa, negative logarithm of the ionization constant of an acid; log P, partition coefficient; H, Henry`s constant.
then defining a working mass of 5 mg. Based on these results, to study kinetics and adsorption equilibrium, eight samples were prepared with 5 mg of adsorbent added to 50 mL of distilled water with sodium acid (0.01% as a antimicrobial agent) [11] , in constant agitation at 90 rpm for 24 h at 25˚C (shaker Arcano model SHZ-88). Later different volumes of the stock solution were added to obtain concentrations of: 5, 10, 15, 20, 25, 30, 35 and 40 mg/L of each respective compound, while maintaining the temperature and agitation constant. Samples of 2.5 mL were taken at different times for up to 312 h for carbamazepine and sildenafil citrate and up to 168 h for methylparaben. The adsorption processes were performed with no buffer addition to control pH to avoid the presence of a new electrolyte in the system. Blank solutions were included to check the pH change, adsorption on the flask walls and the methanol interference on the adsorption assays. The concentration of each solute remaining in the water phase was monitored using a spectrophotometer UV/Vis (Shimadzu model UV-1203). The working wavelength were determined using solutions of 100 mg/L for each compound, observing the clearest peaks at 285 nm, 291 nm and 256 nm for Cbz, Sli and Mp, respectively. The quantification and detection limits were for Cbz, Sil and Mp: 200, 500 and 100 μg/L, and 60, 160 and 30 μg/L, respectively.
The quantities of the PPCPs adsorbed onto activated carbon were calculated as:
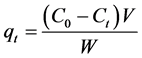 (1)
(1)
where qt is the quantity (in mg/g) of PPCP adsorbed at time t, C0 the initial concentration (in mg/L), Ct the concentration (mg/L) remaining in solution at time t, V (L) the volume of the solution, and W (g) the weight of carbon used.
We used the models of Langmuir in Equation (2) and of Freundlich in Equation (3) for adjustment of the data of the adsorption isotherms by means of the following expressions:
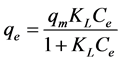 (2)
(2)
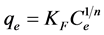 (3)
(3)
where Ce is the concentration of adsorbate (in mg/L), at equilibrium, qe the amount adsorbed per unit mass of adsorbent at equilibrium (in mg/g), qm the maximal adsorption in the active-carbon monolayer, and KL the adsorption constant at equilibrium (in L/mg) for the Langmuir model, it being related to the energy of adsorption. KF is the equilibrium constant for the model of Freundlich and is related to the affinity between the adsorbent and the adsorbate; and if 1/n is 1, the adsorption is favorable.
We investigated the adsorption kinetics utilizing the pseudo-first-order model in Equation (4) and the pseudo second-order one in Equation (5). Those two linear equations for rate are the following:
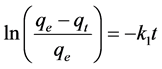 (4)
(4)
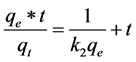 (5)
(5)
where qt and qe are the mass (in mg) of adsorbate adsorbed per gram of adsorbent at time t and at equilibrium, respectively; k1 the apparent-rate constant for the pseudo- first-order equation; and k2 the rate constant for the pseudo second-order equation.
3. Results and Discussion
Two factors are important in the adsorption of the selected compounds. In fact, the adsorption of these PPCPs is a slow process. Therefore, for the practical point of view, a minimal quantity of activated carbon is required to allow the kinetic evaluation within a reasonable time window, and to assure the reproducibility of the experimental results. Thereby, a mass of 5 mg of activated carbon was selected for this study.
The pH before and after of the adsorption processes ranged between 6.4 - 6.6 for Cbz, 6.2 - 6.4 for Sil, 6.4 - 6.5 for Mp and 6.4 - 6.6 for the control solution with no PPCPs, showing no significant variations between tests and control. No noticeable adsorption on glass walls was registered according our tests with PPCPs solutions with no carbon. Additionally, no statistical differences were observed in treatments with and without methanol assessed by means of a t-test comparison.
The study of adsorption isotherms were analyzed with the Langmuir equation that accurately adjusted according to the data obtained (cf. Table 2 and Figure 1). The final value for qe obtained in the adsorption curves for the three compounds (cf. Figure 2) was used in calculations.
The equilibrium concentration qe is also required to analyze the adsorption kinetics; however, this was not possible for most of our results, as shown in Figure 2. Alternatively, an analysis of trial and error could be applied to determine qe, nevertheless, the
Figure 1. Adsorption isotherms for methylparaben at 168 h (circles), carbamezapine at 312 h (triangles), and sildenafil citrate at 312 h onto granular activated carbon. The errors are indicated by bars bracketing each point. The lines represent the goodness of fit to the model of Langmuir.
Figure 2. Adsorption-kinetics curves for methylparaben (Mp), carbamezapine (Cbz), and sildenafil citrate (Sil) onto granular activated carbon. The errors are indicated by bars bracketing each point. The lines correspond to the nonlinear adjustment described in Equation (9) for 5 mg/L (black circles), 10 mg/L (white circles), 15 mg/L (black squares), 20 mg/L (white squares), 25 mg/L (black diamonds), 30 mg/L (white diamonds), 35 mg/L (black triangles), and 40 mg/L (white triangles).
Table 2. Parameters for the experimental data obtained from the adjustment of the Langmuir equation.
error of this evaluation becomes greater in the solutions of lower concentration, which complicates evaluating whether the kinetics follow any of the expressions described in Equation (4) and Equation (5).
At concentrations of 40 mg/L, methylparaben is the only compound which reached equilibrium as shown in the Figure 3. Cbz and Sil should follow the same behavior as Mp when Equations (4) and (5) are used to study their kinetics. According to the analysis of the adsorption kinetics for Mp, at the higher initial concentrations (30 mg/L, 35 mg/L and 40 mg/L) in which the point of equilibrium was attained, we determined that the kinetic model of adsorption most precisely adjusted for the three concentrations was the one of pseudo first order, with apparent-rate constants (k1) of 0.026 ± 0.010 /h, 0.026 ± 0.020/h and 0.028 ± 0.020/h, and the equilibrium adsorptions were 160 ± 25 mg/g, 167 ± 23 mg/g and 164 ± 32 mg/g for initial concentrations of 30 mg/L, 35 mg/L and 40 mg/L, respectively.
Different approaches have been taken into account by several authors to study the adsorption kinetics of a contaminant dissolved in an aqueous system. The process has been explained by means of pseudo first and second order kinetics [12] - [14] . In the present investigation, we analyzed this process by using a nonlinear model that permitted a determination of the rate constant not requiring a knowledge of the value of qe.
The adsorption kinetics was studied considering a reversible process. If θ is the surface coverage fraction at the time t, and C is the concentration of the adsorbate in the solution, the rate of adsorption is given by the difference between the adsorption rate and desorption rate as follows
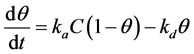 (6)
(6)
If C0 is the initial concentration (in mg/L), ka and kd the adsorption and desorption rate constants, then the remainder concentration C can be written as C = C0 − bq where bq is the adsorbed concentration and β has units of mg/L (see annex: evaluation of β).
After introducing C = C0 − bq in the Equation (6) and regrouping, the following expression can be obtained
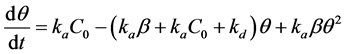 (7)
(7)
Redefining as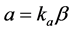 ;
; 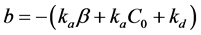 and
and , the Equation (7) takes the form
, the Equation (7) takes the form
Figure 3. Experimental data for methylparaben (circles), carbamazepine (triangles), and sildenafil citrate (diamonds) at initial concentrations (C0) of ca. 40 mg/L for a comparison of the kinetics of adsorption onto granular activated carbon. In the figure, the residual concentration in the solution is plotted on the ordinate as a function of time in h on the abscissa.
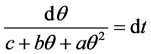 (8)
(8)
Developing the integration [15] of the last differential equation and by rearrangement of terms, Equation (9) can be obtained as described in the annex: integration of Equation (8).
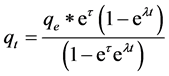 (9)
(9)
Equation (9) can be analyzed by nonlinear regression and for convenience we will define the magnitudes A = qe, B = λ, and C = eτ. Figure 2 and Table 3 summarize the results for the adjustment and the analysis of the regression with respect to Equation (9).
The values for the parameter C obtained for each datum studied in the present work were much greater than 1. Therefore, in Equation (9) if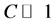 , the following is obtained (the complete analysis is shown in the annex: analysis of the parameter λ).
, the following is obtained (the complete analysis is shown in the annex: analysis of the parameter λ).

In Equation (10), λ represents the rate constant k1, according to Equation (4).
Furthermore, since A = qe (Table 3), θe = qe/qm and by rearranging of terms, now the Equation (7) results in the following (see annex: evaluation of qm)

A linear dependence is observed between 1/qe and 1/C0, from which the maximum adsorption capacity (qm) and the global equilibrium constant (K) values are obtained through the intercept and slope, respectively. The results are presented in Table 4.
Table 3. Values calculated for the parameters A and B, obtained using the nonlinear regression (Equation (9)).
C0 = initial concentration (mg/L); A = qe in (mg/g) and B = λ = k1 in (1/h).
Table 4. Results obtained for the parameters K and qm by means of Equation (11) and values calculated for the adsorption constant ka and the desorption constant kd obtained from the linear function of B versus C0.
Furthermore, the analysis of the parameter B as a function of C0 exhibits a linear behavior (
With the calculated value of qm, the parameter β can be evaluated and defined as (see annex: Evaluation of β)

where mc is the mass (g) of sorbent, qm is the maximum capacity of sorbent, and V is the volume of solution (L).
This parameter permits discrimination between a kinetic of pseudo first order and one of pseudo second order. Then, if
Another alternative for analyzing the behavior of the system is based on an analysis of the initial rate [16] . The estimation of the initial rate from the experimental data was taken from the first pair of points on the graph of qt versus t (Figure 2). Figure 4 shows the values of the initial rate as a function of concentration, where
Figure 4. Initial rate (ν0)―both experimental (data figures) and theoretical (represented by the lines of regression, cf. Equation (14))―is plotted on the ordinate as a function of the initial concentration (C0) of methylparaben (black circles), carbamezapine (white circles), and sildenafil citrate (triangles) indicated on the abscissa.
Table 5. Results obtained for the parameter βθ.
*βθ (mg/L).
represents the slope of a straight line passing through the origin. Therefore, this behavior strongly suggest a pseudo first order kinetic, consistent with the analysis developed previously (Annex, Section: Analysis of the parameter λ) and Table 5 (for
If in Equation (9), qt is derived respect to time, the Equation (13) is obtained and then the rate of adsorption at a given time can be determined as shown in the annex (Expression of the rate of adsorption in terms of the model) and Figure 5.

where


The limit as t → 0 gives the expression for the initial rate (Equation (14)), as shown in Figure 4 and Table 6 (See annex: Expression of the rate of adsorption in terms of the model).
Figure 5. Comparison of the experimental rates (ѵexp) and the evaluated from the Equation (13) (ѵt) as a function of time for (Mp) methylparaben, (Cbz) carbamazepine and (Sil) sildenafil citrate, for 5 mg/L (crosses), 10 mg/L (triangles up), 15 mg/L (triangles down), 20 mg/L (stars), 25 mg/L (circles), 30 mg/L (squares), 35 mg/L (diamonds), and 40 mg/L (hexagons). The solid line corresponds to the linear regression and the long dashes correspond to the confidence 95% interval.
Table 6. Parameters obtained from the analysis of the initial velocity (experimental and theore- tical) as a function of the initial concentration of each of the compounds studied.

As it can be seen in Table 6, Figure 4 and Figure 5, the values obtained from theoretical equations and experimental data show a good agreement, allowing calculating the initial rate and the velocity of a system at a given time.
In the example of Mp, concentrations of 30 mg/L, 35 mg/L and 40 mg/L, did not show significant differences between data obtained from the different models―i.e., pseudo-first-order, nonlinear, initial rate by means of experimental data and the theoretical treatment. These considerations allow working on the basis of these models by combining the Equations (9) and (14) to evaluate the order of the kinetics. This non lineal model can be useful because, in certain studies [17] - [19] the adsorption kinetics and equilibrium could not be clearly defined using traditional models.
Maximum adsorption capacity for Cbz and Mp according the non-lineal regression analysis is approximately 300 mg/g. Similar results were reported for the adsorption of Cbz onto the granular activated carbon obtained from peach seeds [20] . Nevertheless, although the activated carbon studied here exhibited a much higher adsorption capacity compared with other more selective adsorbents like clay minerals, industrial and agricultural wastes [7] [11] , the time required to reach equilibrium was six days for Mp and over 14 days for Cbz and Sil. Similar adsorption times were obtained by Yu et al. [21] for the adsorption of naproxyn, Cbz, and nonylphenol onto the activated carbons commonly used in water-purification plants (e.g., Calgon Carbon F-400™ and PICATIFTE™ carbon made from coconut). In the same way, Rossner et al. [11] demonstrated the high adsorption capacity from carbon, obtained from coconut shells for removal of emergent contaminants from lake water, but without taking into account the lengthy period of contact necessary to achieve the results. Consequently, the potential use of commercial carbon with similar surface area for contaminant removal on a full scale will require further investigation involving steps such as the design of a set of columns, proportion and types of sorbent materials, or combination of different treatment technologies.
4. Conclusions
In the present work we performed studies on the kinetics and equilibrium of adsorption onto granular activated carbon for the purpose of demonstrating the viability of that technique for the elimination of three representative emergent contaminants―Mp, Cbz, and Sil―from aqueous solutions. The granular activated carbon used exhibited a high adsorption capacity for the three compounds at about 300 mg/g for Mp and Cbz and 150 mg/g for Sil (this molecule doubles the surface area respect the two others), but with a slow adsorption kinetics that required mean adsorption times of more than 168 h for the compounds to eventually reach equilibrium in the following order of completion: Mp < Cbz < Sil (Figure 3). Moreover, the time needed for these substances to reach the equilibrium increases progressively upon reduction of their initial concentration. Such excessively lengthy equilibrium kinetics will necessarily complicate the analysis of the adsorption parameters through the traditionally proposed equations because the use of the latter requires the attainment of equilibrium.
The adjustment of the nonlinear model proposed in Equation (9) allows the evaluation of the parameters of the adsorption kinetics, specifically qe and qm, employing experimental results in those system where the adsorption does not attain the saturation equilibrium. On the basis of this model, we determined that the parameter βθ was much lower than C0, and hence the adsorption follows a pseudo first order kinetics. Suppositions on the kinetic order of adsorption or an analysis by trial and error test were not required.
From the knowledge of the adjustment of the data provided by Equation (9), an equation for the initial rate of adsorption can be deduced and compared with the experimental results under the previous analysis that showed that βθ = C0 as seen in Table 5. The estimated behavior for initial rate as function of the initial concentration is similar to that of rates obtained from experimental data as seen in Table 6 and Figure 4. These considerations allow us to conclude that the adsorption processes on granular carbon follow a pseudo-first-order kinetics for the tested compounds.
The results presented in this study have enabled us to obtain valuable information on the interaction of emergent contaminants with a commercial activated carbon. The use of granular carbon in water treatment plants for PPCPs removal should contemplate the slow adsorption rate at the moment of designing a reactor employing this material. To enhance the efficiency of removal further technology design of adsorption devices or combined technological approaches should be taken into account.
Acknowledgements
Dr. Donald F. Haggerty, a retired academic career investigator and native English speaker edited the final version of the manuscript. Funds were from PICT 2014 0919 Project from the Agencia Nacional de Promoción Científica y Tecnológica and Project X733 from the Universidad Nacional de La Plata.
Cite this paper
Delgado, N.Y., Capparelli, A.L., Marino, D.J., Navarro, A.F., Peñuela, G.A. and Ronco, A.E. (2016) Adsorption of Pharmaceuticals and Personal Care Products on Granular Activated Carbon. Journal of Surface Engineered Materials and Advanced Technology, 6, 183-200. http://dx.doi.org/10.4236/jsemat.2016.64017
References
- 1. Elorriaga, Y., Marino, D., Carriquiriborde, P. and Ronco, A. (2013) Human Pharmaceuticals in Wastewaters from Urbanized Areas of Argentina. Bulletin of Environmental Contamination and Toxicology, 90, 397-400.
http://dx.doi.org/10.1007/s00128-012-0919-x - 2. Gracia, E., Martínez, M., Sancho, J.V., Peñuela, G. and Hernández, F. (2012) Multi-Class Determination of Personal Care Products and Pharmaceuticals in Environmental and Wastewater Samples by Ultra-High Performance Liquid-Chromatography-Tandem Mass Spectrometry. Talanta, 99, 1011-1023.
http://dx.doi.org/10.1016/j.talanta.2012.07.091 - 3. Kasprzyk, B., Dinsdale, R.M. and Guwy, A.J. (2008) The Occurrence of Pharmaceuticals, Personal Care Products, Endocrine Disruptors and Illicit Drugs in Surface Water in South Wales, UK. Water Research, 42, 3498-3518.
http://dx.doi.org/10.1016/j.watres.2008.04.026 - 4. Boyd, G.R., Reemtsma, H., Grimm, D.A. and Mitra, S. (2003) Pharmaceuticals and Personal Care Products (PPCPs) in Surface and Treated Waters of Louisiana, USA and Ontario, Canada. Science of the Total Environment, 311, 135-149.
http://dx.doi.org/10.1016/S0048-9697(03)00138-4 - 5. Stackelberg, P.E., Furlong, E.T., Meyer, M.T., Zaugg, S.D., Henderson, A.K. and Reissman, D.B. (2004) Persistence of Pharmaceutical Compounds and Other Organic Wastewater Contaminants in a Conventional Drinking-Water-Treatment Plant. Science of the Total Environment, 329, 99-113.
http://dx.doi.org/10.1016/j.scitotenv.2004.03.015 - 6. Bolong, N., Ismail, A.F., Salim, M.R. and Matsuura, T. (2009) A Review of the Effects of Emerging Contaminants in Wastewater and Options for Their Removal. Desalination, 239, 229-246.
http://dx.doi.org/10.1016/j.desal.2008.03.020 - 7. Grassi, M., Kaykioglu, G., Belgiorno, V. and Lofrano, G. (2012) Removal of Emerging Contaminants from Water and Wastewater by Adsorption Process. Springer, Netherlands.
http://dx.doi.org/10.1007/978-94-007-3916-1_2 - 8. Nielsen, L., Biggs, M.J., Skinner, W. and Bandosz, T.J. (2014) The Effects of Activated Carbon Surface Features on the Reactive Adsorption of Carbamazepine and Sulfamethoxazole. Carbon, 80, 419-432.
http://dx.doi.org/10.1016/j.carbon.2014.08.081 - 9. Ho, Y.S. (2006) Review of Second-Order Models for Adsorption Systems. Journal of Hazardous Materials, 136, 681-689.
http://dx.doi.org/10.1016/j.jhazmat.2005.12.043 - 10. Plazinski, W. (2010) Applicability of the Film-Diffusion Model for Description of the Adsorption Kinetics at the Solid/Solution Interfaces. Applied Surface Science, 256, 5157-5163.
http://dx.doi.org/10.1016/j.apsusc.2009.12.083 - 11. Rossner, A., Snyder, S.A. and Knappe, D.R.U. (2009) Removal of Emerging Contaminants of Concern by Alternative Adsorbents. Water Research, 43, 3787-3796.
http://dx.doi.org/10.1016/j.watres.2009.06.009 - 12. Azizian, S. (2004) Kinetic Models of Sorption: A Theoretical Analysis. Journal of Colloid and Interface Science, 276, 47-52.
http://dx.doi.org/10.1016/j.jcis.2004.03.048 - 13. Limousin, G., Gaudet, J.P., Charlet, L., Szenknect, S., Barthès, V. and Krimissa, M. (2007) Sorption Isotherms: A Review on Physical Bases, Modeling and Measurement. Applied Geochemistry, 22, 249-275.
http://dx.doi.org/10.1016/j.apgeochem.2006.09.010 - 14. Derylo, M.A., Marczewski, A.W., Winter, S. and Sternik, D. (2010) Studies of Adsorption Equilibria and Kinetics in the Systems: Aqueous Solution of Dyes-Mesoporous Carbons. Applied Surface Science, 256, 5164-5170.
http://dx.doi.org/10.1016/j.apsusc.2009.12.085 - 15. Lide, D.R. (2004) Handbook of Chemistry and Physics. CRC Press, Florida.
- 16. Benson, S.W. (1960) The Foundations of Chemical Kinetics. McGraw-Hill, New York.
- 17. Cai, N. and Larese, C.P. (2014) Sorption of Carbamazepine by Commercial Graphene Oxides: A Comparative Study with Granular Activated Carbon and Multiwalled Carbon Nanotubes. Journal of Colloid and Interface Science, 426, 152-161.
http://dx.doi.org/10.1016/j.jcis.2014.03.038 - 18. Chang, E.E., Wan, J.C., Kim, H., Liang, C.H., Dai, Y.D. and Chiang, P.C. (2015) Adsorption of Selected Pharmaceutical Compounds onto Activated Carbon in Dilute Aqueous Solutions Exemplified by Acetaminophen, Diclofenac, and Sulfamethoxazole. The Scientific World Journal, 2015, 11.
http://dx.doi.org/10.1155/2015/186501 - 19. Stoykova, M. and Koumanova, B. and Mörl L. (2013) Adsortive Removal of Carbamazepine from Wastewater by Activated Charcoals. Journal of Chemical Technology and Metallurgy, 48, 469-474.
- 20. Torrellas, S.á., García, L.R., Escalona, N., Sepúlveda, C., Sotelo, J.L. and García, J. (2015) Chemical-Activated Carbons from Peach Stones for the Adsorption of Emerging Contaminants in Aqueous Solutions. Chemical Engineering Journal, 279, 788-798.
http://dx.doi.org/10.1016/j.cej.2015.05.104 - 21. Yu, Z., Peldszus, S., Huck, P. and Peter, M. (2015) Adsorption of Selected Pharmaceuticals and Endocrine Disrupting Compound by Granular Activated Carbon. Adsorption Capacity and Kinetics. Environmental Science & Technology, 43, 1467-1473.
http://dx.doi.org/10.1021/es801961y
Annex
Evaluation of b:
Considering the adsorption kinetics as a reversible process for a regent Z on a solid S
The adsorption rate can be expresses as seen in Equations (6) and (7). The magnitude b is required in order to analyze the adsorption kinetics.
As defined in the text, C is the concentration of the adsorbate in the solution at time t; which can be written as given by
βθ is the adsorbed concentration of the substrate, where the parameter β expresses the moles adsorbed per volume unit (mol/L). At the adsorption equilibrium b can be expressed in terms of θe (i.e. coverage fraction at equilibrium) and Ce (i.e. concentration of the adsorbate at equilibrium). Then, Ce = C0 − βθe and β = (C0 − Ce)/θe.
Therefore β can be evaluated in terms of experimental data as


where mc is the mass (g) of sorbent, qm is the maximum capacity of sorbent, Mw is the molar weight of solute (g/mol) and V is the volume of solution (L).
Integration of Equation (8)
We have seen that


As seen in the literature [15] the solution is possible if the term

Renaming the terms in the previous equation as




Applying the antilogarithm and reorganizing the last equation, the following expression can be obtained for θ

Taking ε as a common factor in the numerator, q is given now by Equation (A6)

At the equilibrium (t → ∞), θe→ −ε/2a and knowing that eτ = γ/ε; the following equation is obtained

The factors from the previous equation can be written in terms of the parameters evaluated experimentally. If θ = qt/qm and θe = qe/qm, so θ/θe = qt/qe and by rearranging, the Equation (A8) is obtained


Where qt, qe and qm are the coverage at the time t, at the equilibrium and at the surface saturation, respectively. The parameters qt, qe and qm are expressed in milligrams of sorbate adsorbed per gram of activated carbon.
By replacing:

Then, plotting qt vs t the regression parameters A, C, and B can be calculated. Results for A and B are listed in Table 3. The C value is higher than 1 in the present conditions. This equation can also be employed in the kinetic analysis of adsorption rates.
Analysis of the Parameter l
As far as C 1 in our system, the following expression can be deduced


Reorganizing,


Therefore, this expression is compatible with a first order kinetics if we identify l with pseudo first order rate constant k1 (See Equation 4 in the text).
Similarly, qe values are obtained from the non-lineal regression analysis (Equation (9) in the text). As far as the C0 βθ at lower q, the term βθ can be ignored in the Equation (7). Then, this equation can be written as

Evaluation of qm
At equilibrium, dθ/dt = 0, and qt becomes qm. The adsorption equilibrium constant K is now = ka/kd. From Equation (7) we obtain qe. Therefore, under the previous assumptions, Equation (A13) is obtained

Knowing that θe = qe/qm we obtain


From the plot of 1/C0 vs 1/qe, the values qm and K are calculated.
Expression of the rate of adsorption in terms of the model.
The theoretical expression for qt obtained previously, 

Applying the distributive property

This equation takes a very simple form introducing the parameters

Then, the adsorption rate as a function of time is given by Equation (A17)

The initial rate expressionν0 is obtained by analyzing the last equation in the limit of
t → 0

As far as C 1, the initial rate of adsorption can be written as follow

This theoretical rate can be tested against the experimental values obtained from the slope of a straight line passing through the origin on the adsorption curve at t = 0 (see Figure 4).










