Journal of Surface Engineered Materials and Advanced Technology
Vol.4 No.2(2014), Article ID:45009,12 pages DOI:10.4236/jsemat.2014.42011
Multilevel B-Spline Repulsive Energy in Nanomodeling of Graphenes
Maharavo Randrianarivony
Virtual Material Design, Fraunhofer Institute for Algorithms and Scientific Computing SCAI, Schloss Birlinghoven, Sankt Augustin, Germany
Email: randrianarivony@ins.uni-bonn.de
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 6 January 2014; revised 5 February 2014; accepted 4 March 2014
ABSTRACT
Quantum energies which are used in applications are usually composed of repulsive and attractive terms. The objective of this study is to use an accurate and efficient fitting of the repulsive energy instead of using standard parametrizations. The investigation is based on Density Functional Theory and Tight Binding simulations. Our objective is not only to capture the values of the repulsive terms but also to efficiently reproduce the elastic properties and the forces. The elasticity values determine the rigidity of a material when some traction or load is applied on it. The pairpotential is based on an exponential term corrected by B-spline terms. In order to accelerate the computations, one uses a hierarchical optimization for the B-splines on different levels. Carbon graphenes constitute the configurations used in the simulations. We report on some results to show the efficiency of the B-splines on different levels.
Keywords:Repulsive Potential, B-Spline, Force, Elastic Stress, Hierarchy

1. Introduction
Nanotechnology is a very important field which has emerged in the last decades and developed very quickly in several directions. It has important applications in various disciplines including aircraft, automobile, electronic and medical engineerings. Nanomaterials admit several important properties which can be exploited in applications. For instance, electric conductivity of nanomaterials is applied in electronic components so that the materials conduct electricity more efficiently than diamonds. Thermal resistivity of nanomaterials can be used to reduce or accelerate heat conduction. It also has a good thermic property so that materials can be designed to resist heat at a very high intensity. Graphene has obtained a significant attention from scientists in the last decades for several reasons. Its material property can be controlled for that it can become a stronger material than steel. The objective in this paper is to use an accurate and efficient fitting of the repulsive energy instead of using a standard parametrization. Many approaches have been proposed to represent empirical estimation of repulsive terms. Before presenting our method, let us briefly survey some traditional repulsive methods. Molecular dynamics employing the Lennard-Jones potential have been well understood so far. It is based upon the well-known potential
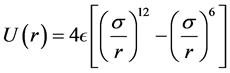 (1)
(1)
which is decomposed into attractive and repulsive components. Since it is only expressed in terms of the inter-atomic distances, it is easy to handle. Due to the simple expression of the potential, it can be differentiated easily and it is not computationally expensive to evaluate. Another important parameterization is the Harrison parametrization:
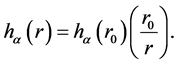 (2)
(2)
The screened Harrison parametrization is an improvement of the former one as provided by
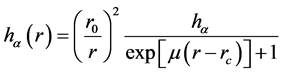 (3)
(3)
where
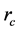 controls the range of the interaction and
controls the range of the interaction and
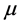 is some parameters obtained by experiments or a fitting process. Sawada parameterization uses the expression
is some parameters obtained by experiments or a fitting process. Sawada parameterization uses the expression
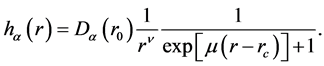 (4)
(4)
The most currently used parametrization is the GSP parameterization (Goodwin-Skinner-Pettifor) which is expressed as
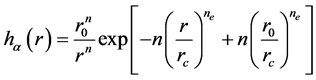 (5)
(5)
where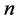 ,
,
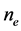 and
and
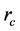 are fitting parameters. Several other methods have been also suggested to achieve some desired properties. Some approaches use certain combinations of known ones.
are fitting parameters. Several other methods have been also suggested to achieve some desired properties. Some approaches use certain combinations of known ones.
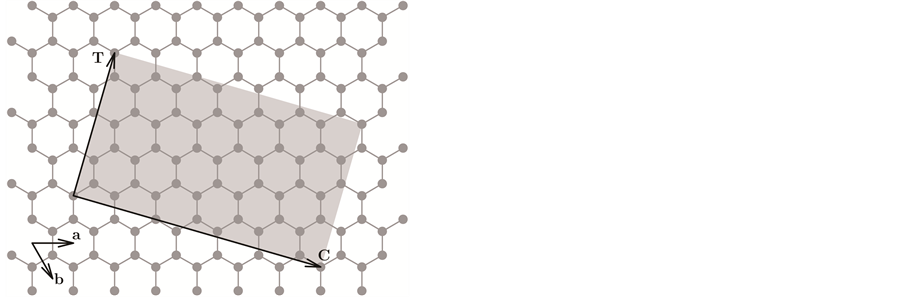
Our motivation is to generate a system which is both accurate and fairly inexpensive to evaluate. We are interested in graphenes and its properties including energy, force and elastic stress. Geometrically, graphenes admit a honeycomb pattern in form of repeated organized hexagons as illustrated in Figure 1(a). They are controlled by the chirality which is a couple of integers
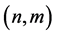 so that
so that . In the case
. In the case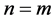 , one has an armchair graphene while
, one has an armchair graphene while
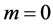 corresponds to the case of a zigzag graphene as in Figure 1(b). Suppose
corresponds to the case of a zigzag graphene as in Figure 1(b). Suppose
 designates the carbon bond length of the graphene. Define
designates the carbon bond length of the graphene. Define
 and
and
 the directive vectors of the honeycomb describing a 2D-lattice so that
the directive vectors of the honeycomb describing a 2D-lattice so that
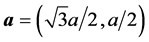 and
and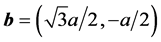 . The chirality indices
. The chirality indices
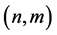 produce the chirality vector
produce the chirality vector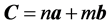 . For the generation of the unit cell, one needs a translational vector
. For the generation of the unit cell, one needs a translational vector
 perpendicular to the chiral vector
perpendicular to the chiral vector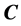 . Let
. Let
 designate the greatest common divisor of
designate the greatest common divisor of
 and
and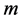 . Define
. Define
 if
if
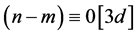 while
while
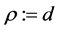 otherwise. The translational vector is expressed by
otherwise. The translational vector is expressed by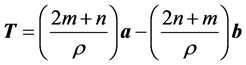 . In the following sections, scaling a graphene amounts to enlarging the unit cells by scaling its primitive vectors. The coordinates of the centers of carbon atoms in the unit cell provided as fractional coordinates within
. In the following sections, scaling a graphene amounts to enlarging the unit cells by scaling its primitive vectors. The coordinates of the centers of carbon atoms in the unit cell provided as fractional coordinates within
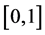 remain unchanged. We are interested in the property of the graphenes as they are confined or stretched as illustrated in Figure 1(c) where we consider a graphene of chirality
remain unchanged. We are interested in the property of the graphenes as they are confined or stretched as illustrated in Figure 1(c) where we consider a graphene of chirality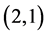 . For significantly confined graphenes, the repulsive energy is very large. For extremely stretched ones, the repulsive energy vanishes so that the energies are the sum of the energies of all constituting atoms.
. For significantly confined graphenes, the repulsive energy is very large. For extremely stretched ones, the repulsive energy vanishes so that the energies are the sum of the energies of all constituting atoms.
 (a)
(a)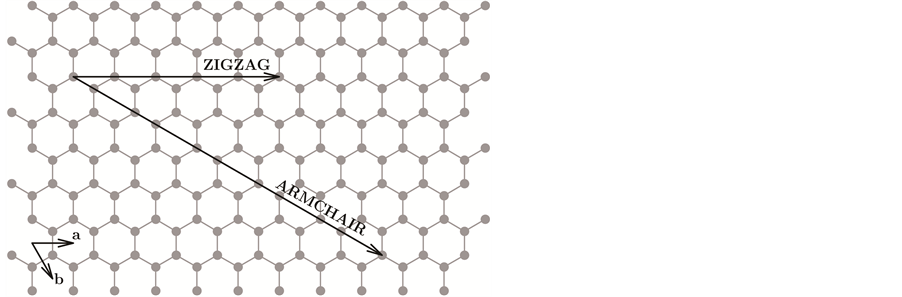 (b)
(b)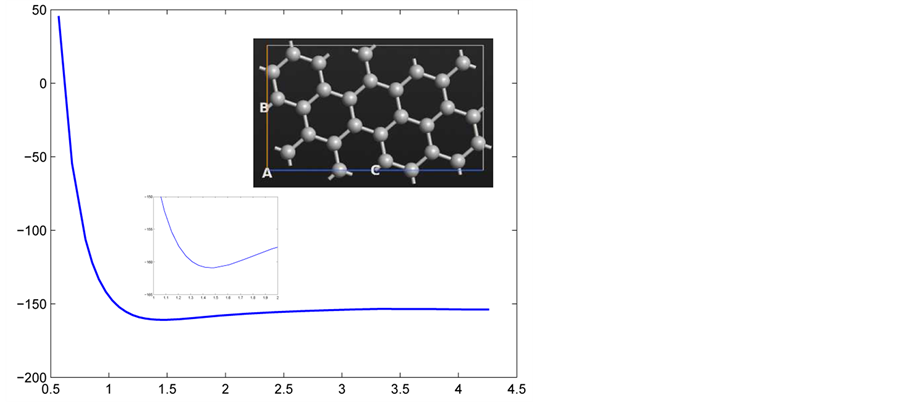 (c)
(c)
Figure 1. (a) Nanosheet: chiral vector
 and translational vector
and translational vector ; (b) Armchair and Zigzag graphene; (c) Ground state energy for graphenes. Confining and enlarging the volume of the graphenes.
; (b) Armchair and Zigzag graphene; (c) Ground state energy for graphenes. Confining and enlarging the volume of the graphenes.
2. Quantum Repulsive Representation
We consider the Born-Oppenheimer or adiabatic approximation assumption stating that the mass and the volume of the atoms are very large in comparison to those of the electrons. The atoms move comparatively slower than the electrons. Thus, we treat the time-independent Hamiltonian operator with respect to the a set of nuclei
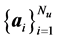 which are supposed to be stationary:
which are supposed to be stationary:
 (6)
(6)
where the coordinates of the
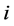 -th electron are denoted by
-th electron are denoted by
 and
and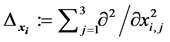 . The above formula describes the kinetic energy along with the nuclear-electron interaction and the inter-electron interaction. Several simplifications of the stationary Hamilton operators have already been proposed. Our proposed potential energy uses two of such simplifications which we survey below.
. The above formula describes the kinetic energy along with the nuclear-electron interaction and the inter-electron interaction. Several simplifications of the stationary Hamilton operators have already been proposed. Our proposed potential energy uses two of such simplifications which we survey below.
For the DFT(Density Functional Theory), one solves one equation for each electron. The Kohn-Sham formalism [1] consists in replacing the complicated single problem into several simpler ones. For each
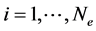
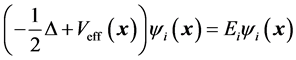 (7)
(7)
where
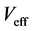 is the effective potential energy which depends implicitly on the total electron density
is the effective potential energy which depends implicitly on the total electron density
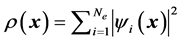 such that
such that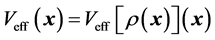 . The problem is then reduced from dimensions
. The problem is then reduced from dimensions
 to
to
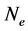 sets of smaller problems of dimension
sets of smaller problems of dimension . The influence of one electron with respect to the other electron is measured by the total electron density. These approaches enable the treatment of Hamiltonian problem even for an electronic structure having a large number of particles on a single desktop. The eigenvalue problem in (7) is nonlinear because its variational [2] [3] operator
. The influence of one electron with respect to the other electron is measured by the total electron density. These approaches enable the treatment of Hamiltonian problem even for an electronic structure having a large number of particles on a single desktop. The eigenvalue problem in (7) is nonlinear because its variational [2] [3] operator
 depends on
depends on

which in turn depends on . It is solved by using a sequence of the linear eigenvalue problems SCF (Self Consistent Field). The effective potential is constituted of the Hartree potential
. It is solved by using a sequence of the linear eigenvalue problems SCF (Self Consistent Field). The effective potential is constituted of the Hartree potential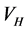 , the exchange correlation potential
, the exchange correlation potential
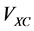 and the external electrostatic field such as
and the external electrostatic field such as
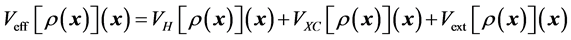
in which the Hartree potential is the inverse of the Poisson operator such as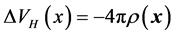 . For its evaluation, either a Poisson problem is solved or one convolves with the Green fundamental solution such as
. For its evaluation, either a Poisson problem is solved or one convolves with the Green fundamental solution such as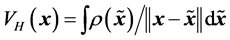 . The main feature of DFT is that one has to approximate the potential by using some correction terms known as exchange-correlation potential [4] [5] . That is usually done by LDA (Local Density Approximation) or GGA (Generalized Gradient Approximation). Analytic expressions of the correlation energy are only known in a few special cases which mainly consist of the high and low density limits. The external electrostatic field potential
. The main feature of DFT is that one has to approximate the potential by using some correction terms known as exchange-correlation potential [4] [5] . That is usually done by LDA (Local Density Approximation) or GGA (Generalized Gradient Approximation). Analytic expressions of the correlation energy are only known in a few special cases which mainly consist of the high and low density limits. The external electrostatic field potential
 is provided by the kernel
is provided by the kernel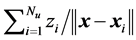 . The above exchange-correlation potential is related to the exchange-correlation energy by
. The above exchange-correlation potential is related to the exchange-correlation energy by
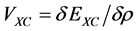 where one expresses
where one expresses
 as the exchange and the correlation parts. In term of the exchange-correlation energy density
as the exchange and the correlation parts. In term of the exchange-correlation energy density
 one has
one has
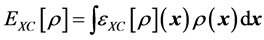 (8)
(8)
where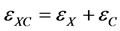 . For the local density approximation (LDA), the exchange energy density is expressed as
. For the local density approximation (LDA), the exchange energy density is expressed as
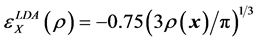 so that
so that . Analytic values of the correlation energy density are only known for some extreme cases. For the high density limit, the exchange correlation energy density is approximated by
. Analytic values of the correlation energy density are only known for some extreme cases. For the high density limit, the exchange correlation energy density is approximated by
 when the Weigner-Seitz radius
when the Weigner-Seitz radius
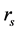 is very small. For the low density limit where
is very small. For the low density limit where
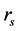 is very large, one has
is very large, one has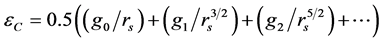 . For other values of
. For other values of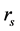 , some interpolation of those extreme values is considered. For example, by using the VWN-approximation (Vosko, Wilk, Nusair) as in [6] , one has
, some interpolation of those extreme values is considered. For example, by using the VWN-approximation (Vosko, Wilk, Nusair) as in [6] , one has
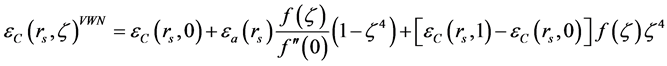
where
 while each one of
while each one of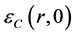 ,
,
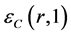 and
and
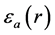 is of the form
is of the form
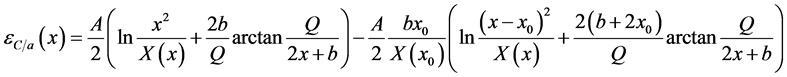
in which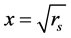 ,
,
 and
and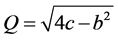 . The constants
. The constants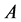 ,
,
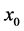 ,
,
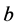 ,
,
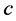 are fitting parameters which are different for
are fitting parameters which are different for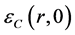 ,
,
 and
and . Once the solutions
. Once the solutions
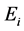 to (7) become known for all
to (7) become known for all , the Khon-Sham approach uses the approximation to
, the Khon-Sham approach uses the approximation to
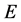 of (6) by
of (6) by
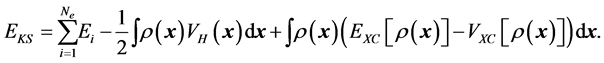
The main improvement from LDA to GGA is that the exchange-correlation energy does not depend only on the total electron density but also on its gradient such as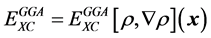 .
.
As a second simplification, we survey the semi-empirical (SE) method using Hueckle method. Consider the spherical coordinates
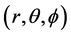 such that
such that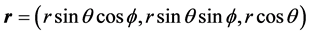 . The spherical harmonics
. The spherical harmonics
 is provided by
is provided by
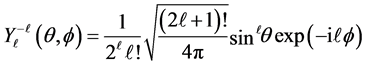
and
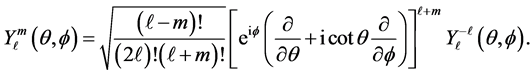
The atomic orbitals sharp (s), principal (p), diffuse (d) and fundamental (f) correspond to linear combinations of
 for
for
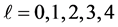 respectively. The basis functions centered at the origin are [7] defined by
respectively. The basis functions centered at the origin are [7] defined by
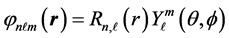 where the radial function
where the radial function
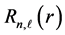 is given by
is given by
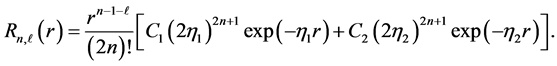
The parameters
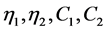 are specified for each atomic orbital. Since one has a set of atomic centers
are specified for each atomic orbital. Since one has a set of atomic centers , one associates to each center
, one associates to each center
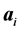 several atomic orbitals and indices
several atomic orbitals and indices . The overlap matrix entry for the centers
. The overlap matrix entry for the centers
 and
and
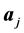 is designated by
is designated by . For the on-site case where the bases are centered at the same atom
. For the on-site case where the bases are centered at the same atom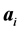 , the SE Hückle method provides
, the SE Hückle method provides . That is, the on-site bases are mutually orthonormal. For the nondiagonal values or off-site cases centered at two different atoms
. That is, the on-site bases are mutually orthonormal. For the nondiagonal values or off-site cases centered at two different atoms
 and
and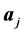 , the entries are computed by a Slater-Koster table lookup where the values are functions of the interatomic coordinates
, the entries are computed by a Slater-Koster table lookup where the values are functions of the interatomic coordinates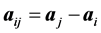 . In fact, the overlap matrix entries can be expanded as
. In fact, the overlap matrix entries can be expanded as
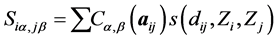
where one uses the inter-atomic distance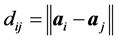 . Computing the integrals by quadrature is too expensive.
. Computing the integrals by quadrature is too expensive.
One stores the expansion coefficients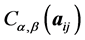 . The value of
. The value of
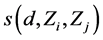 are stored in Slater-Koster table. It does not depend on the coordinates of
are stored in Slater-Koster table. It does not depend on the coordinates of
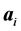 and
and
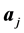 but only on the inter-distance (see [7] for similar discussion). For the Hamiltonian of the SE Hückle, the on-site situation with respect to the center
but only on the inter-distance (see [7] for similar discussion). For the Hamiltonian of the SE Hückle, the on-site situation with respect to the center
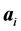 is
is
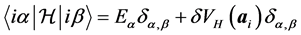
where
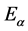 is approximately the eigenenergy for index
is approximately the eigenenergy for index . The off-site term is
. The off-site term is
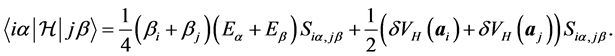
The value of
 is the solution to
is the solution to . This partial differential equation needs to be solved for every evaluation of the Hartree term
. This partial differential equation needs to be solved for every evaluation of the Hartree term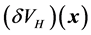 . In the Atomistix Toolkit package [7] , that is solved by a fast multigrid solver. The coefficient
. In the Atomistix Toolkit package [7] , that is solved by a fast multigrid solver. The coefficient
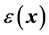 is a dielectric coefficient [8] and
is a dielectric coefficient [8] and
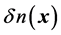 is a certain induced electron density.
is a certain induced electron density.
As a matter of fact, the SE empirical method is much more efficient than the DFT method in term of computational speed. But the DFT computation produces much more accurate results. As a consequence, one searches a certain correction term for the SE method in such a way that the resulting method keeps the efficiency of the SE method while approximating the quality of the DFT approach. The ultimate objective is thus to find a repulsive term to add to the SE energy as described below. We want to generate a repulsive term which conserves most of the properties from the DFT computation. For a configuration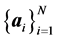 , we intend to conserve the energy
, we intend to conserve the energy
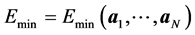 such that
such that . In addition, we are also interested in approximating the forces. For each atom
. In addition, we are also interested in approximating the forces. For each atom , the corresponding force is
, the corresponding force is

such that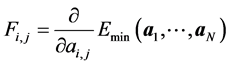 . In addition, we focus also on the elastic property of the graphenes [9] . In general, this property determines the rigidity of a graphene when a traction is applied on it. The strain tensor which is
. In addition, we focus also on the elastic property of the graphenes [9] . In general, this property determines the rigidity of a graphene when a traction is applied on it. The strain tensor which is
 (9)
(9)
is represented in the longitudinal, transversal and normal components. The stress
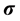 is also represented in a similar tensor way. The strain is related to the displacement
is also represented in a similar tensor way. The strain is related to the displacement
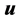 having components
having components
 by
by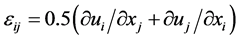 . The correlation between the strain
. The correlation between the strain , stress
, stress
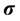 and displacements
and displacements
 is governed by some elasticity equation [9] . Practically, the stress contains implicitly some property of the second derivatives of the energy for the reason that it is the derivative of the energy with respect to strains which are functions of the gradients of the displacements
is governed by some elasticity equation [9] . Practically, the stress contains implicitly some property of the second derivatives of the energy for the reason that it is the derivative of the energy with respect to strains which are functions of the gradients of the displacements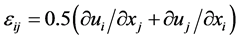 .
.
For a set
 of graphene configurations, the ideal objective functional for the nonlinear optimization is
of graphene configurations, the ideal objective functional for the nonlinear optimization is
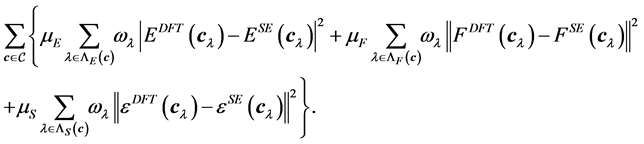 (10)
(10)
In the above expression,
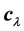 designates a scaling of a configuration
designates a scaling of a configuration
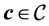 by a factor of
by a factor of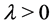 . In addition,
. In addition,
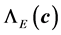 ,
,
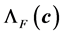 ,
,
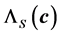 are sets of scaling factors with respect to the reference configuration
are sets of scaling factors with respect to the reference configuration
 for the energy, force and stress respectively. Now, we show the construction of
for the energy, force and stress respectively. Now, we show the construction of
 and
and
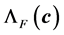 where considers the interval
where considers the interval
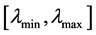 which prescribes the range of interest. That interval contains the optimal factor
which prescribes the range of interest. That interval contains the optimal factor
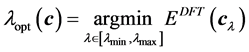 obtained from a geometry optimization. The construction is performed in several steps as depicted in Figure 2. As a first step, one refines the interval
obtained from a geometry optimization. The construction is performed in several steps as depicted in Figure 2. As a first step, one refines the interval
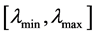 uniformly. Afterwards, one refines gradually in the vicinity of the optimal scaling factor
uniformly. Afterwards, one refines gradually in the vicinity of the optimal scaling factor
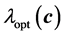 of the configuration
of the configuration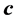 . The principal objective for that construction is to accumulate many points in the neighborhood of the optimum
. The principal objective for that construction is to accumulate many points in the neighborhood of the optimum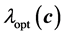 . The determination of the stress is computationally more intensive compared to the computation of the energies. That situation holds even for the case of semi-empirical Hueckle method. The computation of stress for the DFT case is even more intensive but it needs only be done once and stored during the whole optimization. As a consequence, one needs only to handle elastic properties at a few positions in the course of the optimization computation. Otherwise, the whole optimization execution would be too slow since the evaluation of the objective functional would be very intensive. For example, the stress is only applied in the neighborhood of the minimal energy in our computation. Generally,
. The determination of the stress is computationally more intensive compared to the computation of the energies. That situation holds even for the case of semi-empirical Hueckle method. The computation of stress for the DFT case is even more intensive but it needs only be done once and stored during the whole optimization. As a consequence, one needs only to handle elastic properties at a few positions in the course of the optimization computation. Otherwise, the whole optimization execution would be too slow since the evaluation of the objective functional would be very intensive. For example, the stress is only applied in the neighborhood of the minimal energy in our computation. Generally,
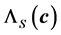 is smaller in size than
is smaller in size than
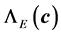 and
and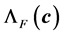 . Not all the range of the scaling factor
. Not all the range of the scaling factor
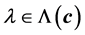 is of the same importance. The vicinity of the optimal scaling factor
is of the same importance. The vicinity of the optimal scaling factor
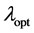 is more valuable because the equilibrium takes place there. As a consequence, one introduces some positive weights to the scaling factors. For our implementation, we used some Gaussian functions centered at the optimal value added by some minimal shift
is more valuable because the equilibrium takes place there. As a consequence, one introduces some positive weights to the scaling factors. For our implementation, we used some Gaussian functions centered at the optimal value added by some minimal shift
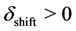 such as
such as
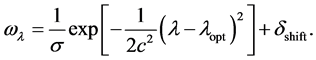 (11)
(11)
The purpose of
 is to prevent the value of
is to prevent the value of
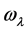 from being practically zero when
from being practically zero when
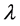 is far from
is far from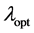 . In our case, we have taken the parameter values to be
. In our case, we have taken the parameter values to be
 and
and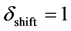 . Since the objective function (10) is very intensive to evaluate, we use in practice its simplification where the forces are provided by finite difference of the energy. Now we would like to describe the parameters with respect to which the nonlinear optimization is performed. The semi-empirical energy with zero repulsive term
. Since the objective function (10) is very intensive to evaluate, we use in practice its simplification where the forces are provided by finite difference of the energy. Now we would like to describe the parameters with respect to which the nonlinear optimization is performed. The semi-empirical energy with zero repulsive term
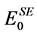 behaves as a pure attractive energy. That is, in order to obtain an energy comparable to the DFT energy, one appends a
behaves as a pure attractive energy. That is, in order to obtain an energy comparable to the DFT energy, one appends a

Figure 2. Construction of .
.
repulsive energy in form of sums of pairwise potential terms such as
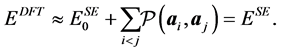
That is, the function
 acts pairwise on the carbon atoms with nuclei coordinates
acts pairwise on the carbon atoms with nuclei coordinates
 and
and
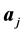 such that
such that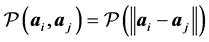 . In other words, the whole process amounts to replacing the repulsive term of the SE energy by an optimal potential energy
. In other words, the whole process amounts to replacing the repulsive term of the SE energy by an optimal potential energy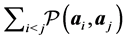 . We search for the optimal pair potential function in the form
. We search for the optimal pair potential function in the form
 (12)
(12)
in which
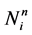 designates B-spline basis functions such that we obtain an energy that behaves very similarly to the DFT in term of energy, force and stress.
designates B-spline basis functions such that we obtain an energy that behaves very similarly to the DFT in term of energy, force and stress.
In the expression (12), the function
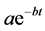 captures the general behavior of the pair potential function
captures the general behavior of the pair potential function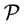 . The role of the B-spline
. The role of the B-spline
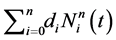 is to correct the small imperfection produced by the principal function
is to correct the small imperfection produced by the principal function . Some cut-off radius
. Some cut-off radius
 is used so that the pair potential function
is used so that the pair potential function
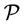 vanishes beyond that value. In our situation, a cut-off radius of about
vanishes beyond that value. In our situation, a cut-off radius of about
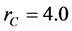 Å suffices completely. In order to obtain zero value and derivative
Å suffices completely. In order to obtain zero value and derivative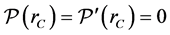 , we insert a short transition function next to the cut-off radius
, we insert a short transition function next to the cut-off radius . One extends
. One extends
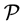 next to the cut-off radius
next to the cut-off radius
 by a polynomial so that one obtains a smooth transition toward zero.
by a polynomial so that one obtains a smooth transition toward zero.
Since the unknown pair potential function is partly expressed in B-spline basis as in (12), we recall briefly some important properties of a B-spline setting. It is in fact a very flexible way of representing piecewise polynomials on any interval of definition . Consider two integers
. Consider two integers
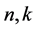 such that
such that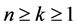 . Suppose the interval
. Suppose the interval
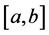 is subdivided by the knot sequence
is subdivided by the knot sequence
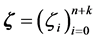 such that
such that
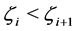 for
for
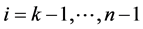 while
while
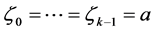 and
and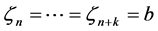 . One defines the B-spline basis functions for
. One defines the B-spline basis functions for
 as
as
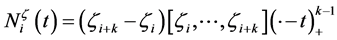
where one employs the divided difference
 in which the truncated power functions
in which the truncated power functions
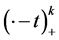 are given by
are given by
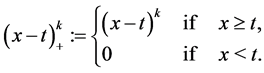
We only focus on B-splines which are internally uniform: except for the boundary multiple knots, all knot entries
 are uniformly spaced. The integer
are uniformly spaced. The integer
 controls the smoothness of the B-spline for which the resulting function admits an overall smoothness of
controls the smoothness of the B-spline for which the resulting function admits an overall smoothness of
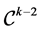 so that the case
so that the case
 corresponds to discontinuous piecewise constant functions. The integer
corresponds to discontinuous piecewise constant functions. The integer
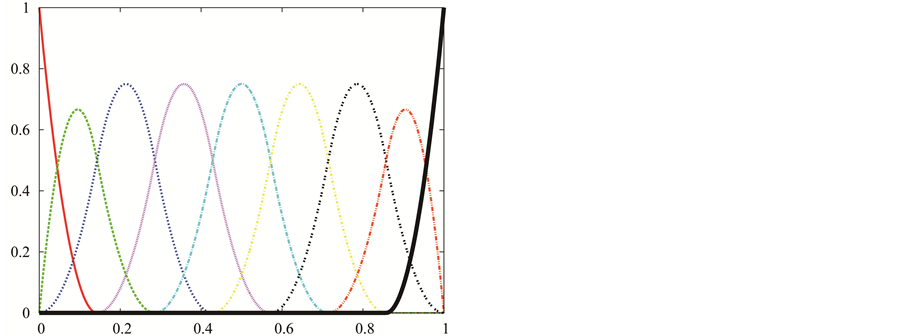
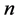 controls the number of B-spline functions. In Figure 3(a), we see some illustration of B-spline bases on an internally uniform knot sequence. Figure 3(b) displays an instance of a B-spline curve defined on
controls the number of B-spline functions. In Figure 3(a), we see some illustration of B-spline bases on an internally uniform knot sequence. Figure 3(b) displays an instance of a B-spline curve defined on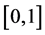 . In Figure 3(c), the knot sequence has been refined uniformly by increasing
. In Figure 3(c), the knot sequence has been refined uniformly by increasing
 to
to
 while keeping
while keeping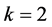 . That is achieved by introducing a new knot entry between every two knots of the B-spline in the former Figure 3(b). For our application, we insert several knots at once so that the new knot sequence is again internally uniform. A new knot entry is inserted between two consecutive old ones. The evaluation of B-spline functions is not calculated by using the above definition but rather by means of the de-Boor algorithm. Since the knot sequence is internally uniform, we use the notation
. That is achieved by introducing a new knot entry between every two knots of the B-spline in the former Figure 3(b). For our application, we insert several knots at once so that the new knot sequence is again internally uniform. A new knot entry is inserted between two consecutive old ones. The evaluation of B-spline functions is not calculated by using the above definition but rather by means of the de-Boor algorithm. Since the knot sequence is internally uniform, we use the notation
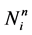 instead of
instead of
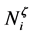 in (12). We will describe next the procedure of inserting new knots into existing ones. That is important when one needs to increase the degree of freedom in the pair potential function in (12). The principal objective is to efficiently express a function defined on the coarse knot sequence in term of B-splines on a fine one. Consider two knot sequences
in (12). We will describe next the procedure of inserting new knots into existing ones. That is important when one needs to increase the degree of freedom in the pair potential function in (12). The principal objective is to efficiently express a function defined on the coarse knot sequence in term of B-splines on a fine one. Consider two knot sequences
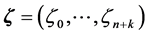 and
and
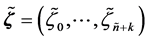 such that
such that . For both knot sequences, the smoothness index
. For both knot sequences, the smoothness index
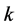 is conserved intact. The following discrete B-splines enable the expression of a coarse basis
is conserved intact. The following discrete B-splines enable the expression of a coarse basis
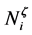 as a linear combination of the fine basis
as a linear combination of the fine basis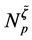 . Choose
. Choose
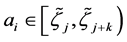 and define
and define
 (a)
(a)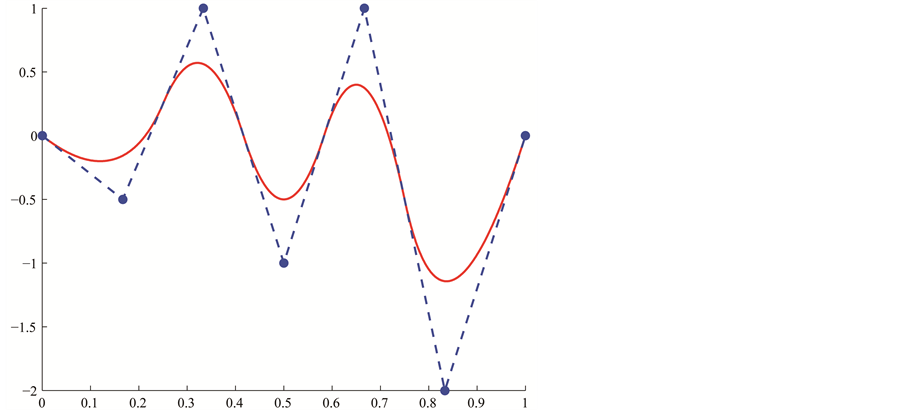 (b)
(b)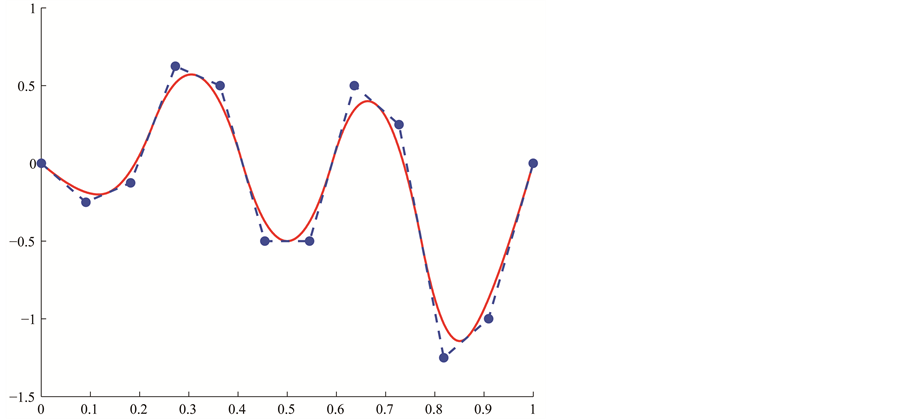 (c)
(c)
Figure 3. (a) B-spline bases; (b) Original B-spline; (c) a finer B-spline which has the same parametrization as the original B-spline.
where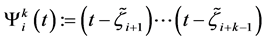 . One has
. One has
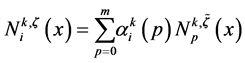
where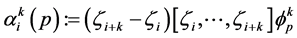 . The discrete B-splines
. The discrete B-splines
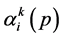 are evaluated by using the recurrence
are evaluated by using the recurrence

in which

In our simulation, we took
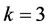 which corresponds to continuously differentiable pair potentials. In Figure 4, we observe some illustration of such knot insertions. Not only the two B-spline functions admit the same image but their parametrizations from their interval of definition
which corresponds to continuously differentiable pair potentials. In Figure 4, we observe some illustration of such knot insertions. Not only the two B-spline functions admit the same image but their parametrizations from their interval of definition
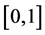 are completely identical.
are completely identical.
The whole process of the determination of the repulsive energy is performed in increasing levels as follows. First, one determines the optimal value for
 without the B-spline part in (12) by using a global optimizer. Then, one fixes the resulting optimal values of
without the B-spline part in (12) by using a global optimizer. Then, one fixes the resulting optimal values of
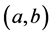 during the subsequent computation. Second, one searches the optimal B-spline
during the subsequent computation. Second, one searches the optimal B-spline
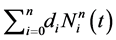 where
where
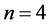 by starting a local optimization with the initial guess
by starting a local optimization with the initial guess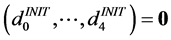 . Now, one repeats the following steps iteratively. Inject the optimal value
. Now, one repeats the following steps iteratively. Inject the optimal value
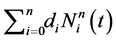
into
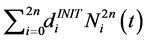 by using the above knot insertion technique where
by using the above knot insertion technique where
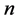 is increased into
is increased into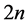 . Apply then a local optimization with respect to
. Apply then a local optimization with respect to
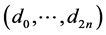 by using,
by using,
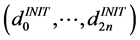 as initial guess.
as initial guess.
3. Computer Implementation
In this section, we report on some practical results of the formerly proposed method. The implementation of the method was realized by combining ATK, NLOPT and python. The ATK (Atomistix ToolKit) has some GUI extension well known as VNL (Virtual NanoLab). We use NLOPT for the diverse nonlinear optimization operations [10] in which both global and local optimizers are involved. A global optimizer searches for the best parameters among all possibilities while a local one searches only inside a local neighborhood of a certain provided starting initial guess. For the global optimizer, we use the NLOPT option GN-CRS2-LM standing for Controlled Random Search with Local Mutation. The local optimizers are performed by using BOBYQA algorithm which is an efficient gradient-free method available in NLOPT. In order to facilitate the combinations of options, we implemented several python classes. The class for the reference configurations organizes the graphene structures to be used together with their respective optimization weights. There is also a class for the optimization parameters specifying the property such as orders and levels of B-splines as well as the abortion criterion. It controls the contribution of the energy, force and stress
 in the optimization functional (10). The construction of the sets
in the optimization functional (10). The construction of the sets
 as well as the interval for the range of interest has been equally supported by some python classes. In order to save computations, one needs to precompute and store the data for the DFT as well as the semi-empirical with zero pair potential.
as well as the interval for the range of interest has been equally supported by some python classes. In order to save computations, one needs to precompute and store the data for the DFT as well as the semi-empirical with zero pair potential.
As a first test, we consider multiple computations for different configurations of graphenes. The configuration
 is based upon the first index
is based upon the first index
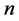 of the chirality parameters
of the chirality parameters
 where
where
 is allowed to vary. That is, each configuration
is allowed to vary. That is, each configuration
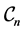 is composed of all graphenes admitting chirality
is composed of all graphenes admitting chirality
 such that
such that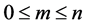 . In Figure 4(a), we observe some comparisons for graphenes in
. In Figure 4(a), we observe some comparisons for graphenes in
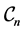 where
where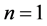 . Most values align on the diagonal which implies the agreement between the outcomes provided by the DFT and the SE methods. Similar tests for graphenes where
. Most values align on the diagonal which implies the agreement between the outcomes provided by the DFT and the SE methods. Similar tests for graphenes where
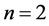 and
and
 are depicted respectively in Figure 4(b), Figure 4(c). The resulting SE energies do not exactly provide the same results as the DFT but the current SE energies should be more reliable in comparison to the empirical potential in (1)-(5) which contain very few parameters. In addition, the speed of computation is much faster for the currently presented SE than the one for DFT. In fact, the execution time of
are depicted respectively in Figure 4(b), Figure 4(c). The resulting SE energies do not exactly provide the same results as the DFT but the current SE energies should be more reliable in comparison to the empirical potential in (1)-(5) which contain very few parameters. In addition, the speed of computation is much faster for the currently presented SE than the one for DFT. In fact, the execution time of
 (a)
(a) (b)
(b) (c)
(c)
Figure 4. (a) Configuration consists of graphene of chirality ; (b)
; (b) ; (c)
; (c)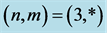 .
.
the SE in comparison to DFT has a speed of factor
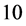 or more. Due to that acceleration gain, the method is in many aspects good to attain efficiency. If the accuracy is not satisfactory, then one has to use the direct DFT with the cost of much more computing time.
or more. Due to that acceleration gain, the method is in many aspects good to attain efficiency. If the accuracy is not satisfactory, then one has to use the direct DFT with the cost of much more computing time.
As a further test, we investigate the decrease of the objective function with regard to the B-spline levels. We consider again the three configurations
 above for
above for . The results of such tests are displayed in Table 1 where the initial line describes the SE with zero pair potential (PP). The next one is the SE with exponential pair potential
. The results of such tests are displayed in Table 1 where the initial line describes the SE with zero pair potential (PP). The next one is the SE with exponential pair potential
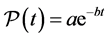 without B-splines. The following ones are the pair potentials with more and more B-splines as in (12). The error barely drops down after level
without B-splines. The following ones are the pair potentials with more and more B-splines as in (12). The error barely drops down after level
 for all graphene configurations
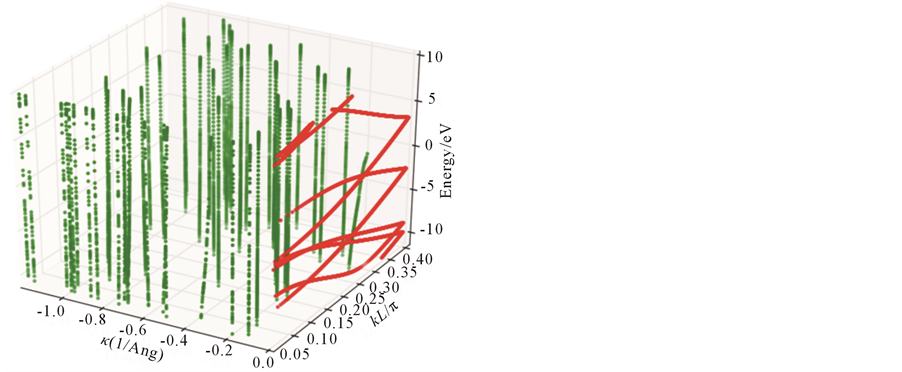
for all graphene configurations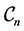 . In fact, the minimal value of the function in (10) is not always zero. As a consequence, one cannot expect an arbitrarily accurate approximation. As a next test, we consider the complex band structures for using the DFT and SE computations whose results are respectively displayed in Figure 5(a), Figure 5(b) for the graphene with chirality
. In fact, the minimal value of the function in (10) is not always zero. As a consequence, one cannot expect an arbitrarily accurate approximation. As a next test, we consider the complex band structures for using the DFT and SE computations whose results are respectively displayed in Figure 5(a), Figure 5(b) for the graphene with chirality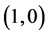 . The plots depict band lines which are not shown as continuous curves but as sets of sampling points. The points which are purely real and explicitly complex are depicted in red and green respectively. In order to provide more validation for the efficiency of the proposed method, some comparison of the elastic properties was performed when computed by means of the DFT and SE methods. In Figure 6, we observe the elastic properties corresponding to the two methods. In general, the stress tensor
. The plots depict band lines which are not shown as continuous curves but as sets of sampling points. The points which are purely real and explicitly complex are depicted in red and green respectively. In order to provide more validation for the efficiency of the proposed method, some comparison of the elastic properties was performed when computed by means of the DFT and SE methods. In Figure 6, we observe the elastic properties corresponding to the two methods. In general, the stress tensor
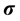 is presented in three directions similar to (9). Nevertheless, we omit the normal components of the stress tensor
is presented in three directions similar to (9). Nevertheless, we omit the normal components of the stress tensor
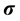 in this particular
in this particular
 (a)
(a) (b)
(b)
Figure 5. Complex band structures. The purely real values are shown differently for : (a) Using DFT; (b) Semiempirical.
: (a) Using DFT; (b) Semiempirical.
 (a)
(a) (b)
(b)
Figure 6. Longitudinal and transversal elastic stress components: (a) graphene ; (b) graphene
; (b) graphene .
.
Table 1. Errors at each B-spline level.
case of the graphene configurations which are planar. In addition, the stress components
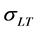 and
and
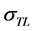 are practically zero for both the DFT and SE computations. As a result, it remains to consider the longitudinal component
are practically zero for both the DFT and SE computations. As a result, it remains to consider the longitudinal component
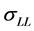 and the transversal component
and the transversal component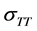 . That is, we need only to compare between
. That is, we need only to compare between
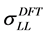 and
and
 as well as
as well as
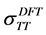 and
and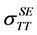 . We concentrate only on
. We concentrate only on
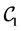 because the other configurations produce similar results. The cases of graphenes admitting chiralities
because the other configurations produce similar results. The cases of graphenes admitting chiralities
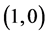 and
and
 are respectively shown in Figure 6(a), Figure 6(b) where one observes the alignments of DFT and SE elasticities. The two results for
are respectively shown in Figure 6(a), Figure 6(b) where one observes the alignments of DFT and SE elasticities. The two results for
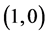 and
and
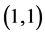 are almost similar except that
are almost similar except that
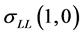 corresponds to
corresponds to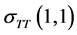 . Geometrically, the transversal direction of the chirality
. Geometrically, the transversal direction of the chirality
 corresponds to the longitudinal direction of the chirality
corresponds to the longitudinal direction of the chirality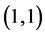 .
.
4. Conclusion
A method was presented to determine the optimal pair potential for the repulsive quantum energy. We concentrated on configurations which are constituted of carbon graphenes. The method was based upon hierarchical B-splines layered on different levels. The principal objective function consists of terms involving not only energies but also forces and elastic stresses. Several computer results validate the reliability of the newly proposed method as compared to outcomes from Density Functional Theory.
References
- Kohn, W. and Sham, L. (1965) Self Consistent Equations Including Exchange Correlation Effects. Physical Review Letters, 140, A1133-A11388. http://dx.doi.org/10.1103/PhysRev.140.A1133
- Harbrecht, H. and Randrianarivony, M. (2011) Wavelet BEM on Molecular Surfaces: Solvent Excluded Surfaces. Computing, 92, 335-364. http://dx.doi.org/10.1007/s00607-011-0147-y
- Randrianarivony, M. (2013) On Space Enrichment Estimator for Nonlinear Poisson-Boltzmann. American Institute of Physics, 1558, 2365-2369.
- Perdew, J. and Wang, Y. (1992) Accurate and Simple Analytic Representation of the Electron-Gas Correlation Energy. Physical Review B, 45, 13244. http://dx.doi.org/10.1103/PhysRevB.45.13244
- Perdew, J. and Zunger, A. (1981) Self-Interaction Correction to Density-Functional Approximation for Many-Electron Systems. Physical Review B, 23, 5048-5079. http://dx.doi.org/10.1103/PhysRevB.23.5048
- Vosko, S., Wilk, L. and Nusair, M. (1980) Accurate Spin-Dependent Electron Liquid Correlation Energies for Local Spin Density Calculations: A Critical Analysis. Canadian Journal of Physics, 58, 1200-1211. http://dx.doi.org/10.1139/p80-159
- Stokbro, K., Petersen, D., Smidstrup, S., Blom, A., Ipsen, M. and Kaasbjerg, K. (2010) Semi-Empirical Model for Nano-Scale Device Simulations. Physical Review B, 82, 075420. http://dx.doi.org/10.1103/PhysRevB.82.075420
- Carbo-Dorca, R. and Bultink, P. (2004) Quantum Mechanical Basis for Mulliken Population Analysis. Journal of Mathematical Chemistry, 36, 231-239. http://dx.doi.org/10.1023/B:JOMC.0000044221.23647.20
- Cadelano, E., Palla, P., Giordano, S. and Colombo, L. (2009) Nonlinear Elasticity of Monolayer Graphene. Physical Review Letters, 102, 235502. http://dx.doi.org/10.1103/PhysRevLett.102.235502
- Johnson, S. The NLopt Nonlinear-Optimization Package. http://ab-initio.mit.edu/nlopt


