Journal of Tuberculosis Research
Vol.2 No.2(2014), Article
ID:46683,11
pages
DOI:10.4236/jtr.2014.22010
Unbiased Multirresistance Prevalences in Real Testing Practices? An Intuitive Correcting Approach Applied to Tuberculosis in Portugal
Cristiana Areias, Teodoro Briz, Carla Nunes
Department of Epidemiology and Statistics, National School of Public Health, University NOVA of Lisbon, Lisbon, Portugal
Email: c.areias@ensp.unl.pt, tshb@ensp.unl.pt, cnunes@ensp.unl.pt
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 March 2014; revised 23 April 2014; accepted 2 May 2014
ABSTRACT
Background: Antibiotics resistance threats Tuberculosis control, being crucial to work on unbiased MDR-TB images. The decision of testing is clinical, non-random, raising extrapolation problems. Aim: To evince and describe non-random testing practices; develop and apply a coherent and intuitive method for estimating global corrected resistance prevalences (2000-2009). Methods: A quantitative approach upon National Tuberculosis Database was undertaken, to assess testing potential predicting factors. Different factors structures in tested and non-tested cases were characterized (regarding socio-demographic and clinical variables), through binary logistic regressions. Estimated multirresistance prevalences were corrected using the essayed model. Results: Only 32% of cases had been tested, where MDR-TB prevalence was 2.38%. All factors influenced the practice of testing (p < 0.05). Corrected resistance estimates in non-tested ranged 1.96% - 2.71%, and the global weighted average found ranged 2.07% - 2.51%, depending on the chosen strata structure. Conclusions: MDR-TB prevalence representation must consider patients’ characteristics influencing testing. The correction method improved prevalences interpretation substantially; corrected and conventional values were close, because tested and non-tested had similar structures. But in other settings or health problems, correcting such estimates can make a relevant difference.
Keywords:Testing Practices, Tuberculosis, MDR-TB

1. Introduction
Epidemiological information is showing consistent improvements in Tuberculosis (TB) control worldwide. Incidence rate is falling since 2002 and mortality is decreasing since the 90s; however TB remains a major Public Health burden in most developing countries, in part due to the HIV epidemic [1] [2] . In Portugal, HIV co-infection (about 15% of new TB cases [3] ), social and behavioral factors and some inefficiencies of health services may explain difficulties in achieving a better control [4] . Progresses must be promoted, particularly in higher risk districts, probably under unfavorable socioeconomic, cultural and organizational influences [4] . Current economic crisis may also counteract control efforts [1] .
A sufficiently high both new cases detection (>70%) and treatment success (>85%) are established as milestones for achieving an acceptable control in a population [2] . Among factors influencing treatment success, the susceptibility of patients’ bacilli to appropriate antibiotics is obviously crucial [5] . Since 1994, World Health Organization (WHO) alerted for the insufficient information about drug resistant Tuberculosis (DR-TB), especially in developing countries, and created the Global Project on Drug Resistance Surveillance [6] [7] . It is a matter of increasing concern, with an unfavorable trend and the stagnancy of antibiotic resources.
Multidrug Resistant Tuberculosis (MDR-TB) occurs when strains of Mycobacterium tuberculosis are resistant to at least both Isoniazid (H) and Riphampicin (R) [8] . DR-TB emerged after the introduction of effective TB treatment as a generalized practice, and MDR-TB has been reported in every country where this phenomenon has been surveyed [9] -[11] . First-line antibiotics, especially H and R, are more potent and usually better tolerated than second-line ones. Consequently, resistance to first-line drugs leads to longer, more expensive treatments (at least 20 months, vs 6 months) [1] and often predicts unsuccessful treatment courses (cure rates: 60% to 75% vs around 90%), in non HIV-infected patients [12] [13] . In addition, MDR-TB and unsuccessful treatment show a dual reinforcement, because they are both predictor and consequence of each other [13] .
Some risk factors are known for a case to be drug resistant, as previous treatment, male sex and HIV co-infection [13] . In countries where HIV infected and TB populations overlap more deeply, a faster increase of MDR-TB has been observed [14] [15] .
In Portugal, TB endemics has a medium-low level at a world scale (in 2010, notified incidence rate was 23.2 × 10−5), representing the least favorable situation in Western Europe, though reducing slowly but firmly [3] [4] , [16] . Since 2000, Portugal improved its Tuberculosis Surveillance System (SVIG-TB), following WHO recommendations, and it is categorized as Class A, the highest classification for the quality of such data [15] . The Portuguese Directorate-General of Health publishes annual reports about the TB epidemiological situation [3] [17] [18] . In 2010, officially reported resistance to both H and R (H∩R) was of 1% in new cases and 5.2% in retreatments. These proportions are low, at a worldwide level [15] . However, a study published in 2000, designed to understand resistant TB in Portugal, revealed relevant proportions of acquired resistance [19] .
Expressing and interpreting results for Drug Susceptibility Tests (DST) can be difficult. The specificity and validity variability of methods used for antibiotics testing may influence results [20] ; and MDR-TB studies undergo small numbers problems frequently; lastly, it is not possible to test all cases, or a random sample of them, because patients don’t all have the required biological specimen available; and DST may be rationally requested, depending on particular patients’ characteristics and on clinicians’ experiences [21] . Beyond the fact that bacilli in non-tested may also have or develop resistances to some antibiotics, the non-random physicians’ decisions may create a selection bias that will distort the final proportion of resistant cases (Figure 1).
Should MDR-TB occurrences found in tested cases be considered as representative of the total number of MDR-TB cases in all notified cases? Or MDR-TB cases found depend on who is tested, representing a nonrandom sample of the total MDR-TB cases?
According to the conventional calculation process, estimates of resistance prevalences assume that tested cases are representative of the whole notified TB cases [22] . Authors believe that such an assumption is not reliable enough, however, as referred to.
A method liable to deal with the described bias is necessary. Methodologically, this can be framed in a nonprobability sampling context, because the selection of elements was based on assumptions regarding the population of interest, as opposed to a random selection. These conditions give rise to an exclusion or selection bias, imposing limits on how much and how good information a sample can provide about the population, making it difficult to extrapolate to it. This sampling method can be called as “Intentional”, where the cases are selected based on who they (doctors) think would be appropriate for the study (testing), drawn on both theory (i.e., scientific literature) and experience, thus not giving to all individuals in the population (TB cases) equal chances
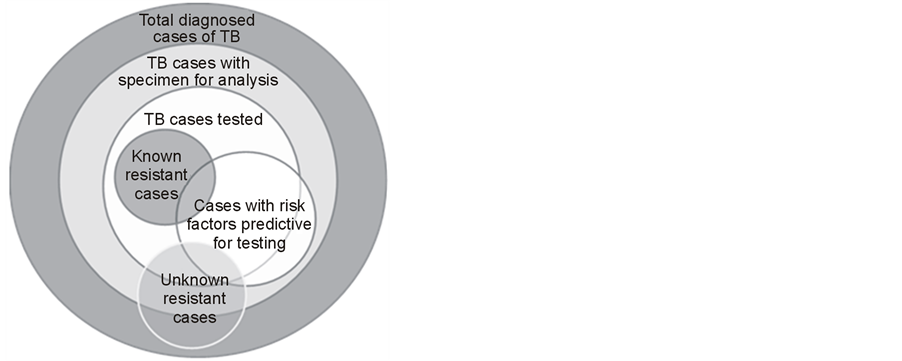
Figure 1. From having Tuberculosis to being tested: some non-tested patients may be resistant and some factors may be predictive for testing.
of being selected. But a purely random selection for testing would involve ethical problems in the field setting, of course [23] .
In this intentional sampling, certain members (i.e. HIV-positive) can be either underrepresented or overrepresented relatively to others in the population. The proposed method to correct the global MDR-TB prevalence is based on the comparison of the characteristics of tested cases, with those of non-tested, and ends up by synthesizing an all-cases global value, weighted for strata dimensions.
Thus, who were the patients in fact tested in practice? What was the importance of the tested patients’ structure regarding their characteristics, as compared with non-tested? And how can this knowledge help to get a proportionate, contextualized view of the overall resistance profile?
On such basis, this essay aimed to: 1) describe and analyze non-random testing practices; 2) develop and assess a coherent and intuitive method for calculating TB global resistance prevalences, which could take into account testing reality; and 3) estimate MDR-TB prevalences for 2000-2009 in Portugal, using each approach. A contribution for sounder decisions in control was envisaged.
2. Methods
This study had a strong methodological component, focusing non-probabilistic sampling, and was based on SVIG-TB database, regarding the period 2000-2009.
Detecting a MDR-TB case can be the end of a complex non-random process, expressed as a conditional probability chain of major steps. A model representation of this chain was built up from SVIG-TB, where the number of patients known or estimated in each step, in 2000-2009, was identified. Each percentage between steps was interpreted as the probability of moving between successive stages.
Notified cases with all kinds of clinical expression were included, as a specimen for culture can be obtained from any clinical presentation, virtually [24] . After a descriptive exploration to testing and treatment practices and the corresponding results, an internal case-control analysis was undertaken. Tested patients were the “cases” and several alternatives for defining the “control group” were faced; all other (non-tested) patients were included in this group at last, because they were acceptable as sufficiently comparable with “study cases”. Such limit-option ended up configuring a cross-sectional approach.
Available variables selected as possible predictors of being tested were: sex, age, HIV serology (positive or negative), previous treatment (presence or absence), being drug abuser (yes or no), being alcoholic: yes or no [25] , and country of birth (natives or foreigners).
As to the response variable, only the initial DST undertaken was considered, because: 1) SVIG-TB records the first and the last DST for each patient merely, meaning that the last test might correspond to different moments in follow-up for different cases; 2) it was expected to assess the existence of predicting factors for the first testing, which was the one relevant for initial treatment definition, in the current scope.
Although only patients tested for H∩R were focused, an initial descriptive study was done considering all antibiotics tested.
A binary logistic regression permitted to explore relationships between TB cases being tested to H∩R and their exposure to a selection of relevant factors predicting testing; the two structures of exposure to these factors in study groups (cases and controls) were compared through odds ratios (a proxy to the relative probabilities of being tested, according to exposure statuses). Crude and adjusted ratios were used to identify such factors, as well as their degree of association with the response variable. PASW Statistics Software (version 18) was used and 95% confidence intervals were calculated, when suitable.
An overall prevalence of MDR was estimated, based on two different approaches: 1) the classical one, assuming the prevalence in tested cases as a competent proxy to global prevalence, considering the sample tested as representative of all cases, similar to the result of a random selection of cases to be tested; 2) a corrected prevalence estimation, considering the differences in distributions of characteristics found to predict testing, between tested and non-tested cases, as detailed next.
The Correcting Method
Assuming that in practice the tested sample wasn’t random, this method intended to yield a corrected estimate of the prevalence of MDR-TB resistant occurrences in all cases, allowing for the differences between the distributions of tested and non-tested, regarding characteristics found to predict testing.
Logistic regression models were applied to identify which variables were relevant, for predicting the probability of being tested. If there were no evidence of different distributions between tested and non-tested cases, the classical approach could be taken (as equal estimates using either method would result).
Underlying assumptions were carefully defined, and attention was paid to the potential biasing effect of excluding cases, because of missing values for any variable.
An important aspect was the assumption that resistance prevalences were equal in equivalent strata in tested and non-tested groups (stratification based on identified predicting factors).
The definition of the factor stratification structure in either tested or non-tested was undertaken, in accordance with several combinations of classes of the factors predicting testing, allowing a specific prevalence estimate for each stratum in non-tested.
For each scenario (each set of characteristics considered for the definition of strata structure), the following method was applied:
1) Considering the identified variables , each group (tested or non-tested) was therefore broken down into a system of cells, or strata
, each group (tested or non-tested) was therefore broken down into a system of cells, or strata ;
;
2) For each cell in tested, known resistance prevalence in stratum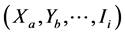 ,
, 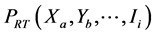 , was identified:
, was identified:
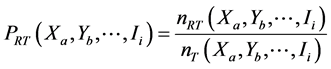 ;
;
where  is the number of resistant tested cases in stratum
is the number of resistant tested cases in stratum ;
; 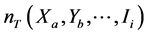 is the number of tested cases in
is the number of tested cases in ;
;
3) In non-tested stratum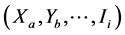 , the number of estimated resistances cases to H∩R was calculated
, the number of estimated resistances cases to H∩R was calculated , by applying the specific proportion of resistances found in this stratum in tested cases:
, by applying the specific proportion of resistances found in this stratum in tested cases:
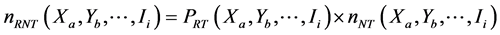 ;
;
where 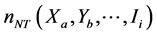 is the number of non-tested cases in stratum
is the number of non-tested cases in stratum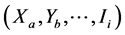 ;
;
4) The total number of resistant cases (nR) was given by the sum of all resistant cases identified among tested, plus the number of resistant cases estimated to exist in non-tested, across all strata:
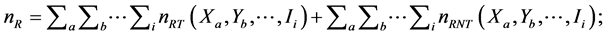
5) The global proportion of corrected resistances (%PCR) was given by the total resistant cases (nR), in either tested (nT) or non-tested (nNT), divided by the total notified cases:
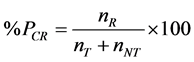 .
.
Figure 2 illustrates the process for a given stratum (previous steps 1 to 3), considering a combination of
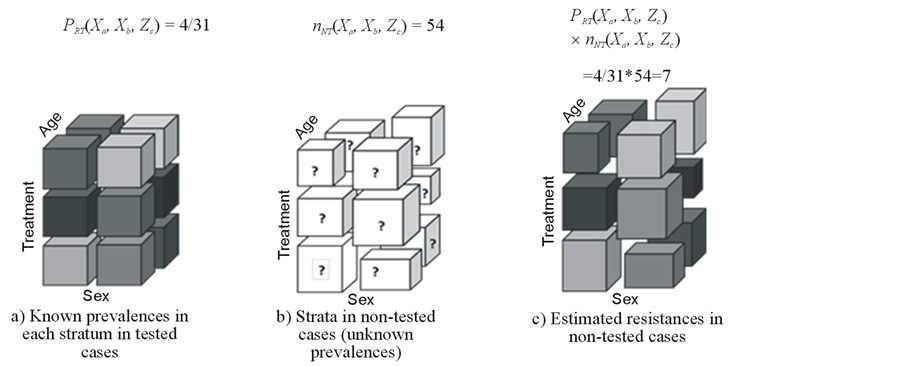
Figure 2. Estimating resistances in non-tested cases, for a given cell (Sex (X) = F, Previous Treatment (Y) = 0, Age (Z) = 35 - 44).
classes of a selected set of factors that might predict the decision of testing.
Therefore, estimated resistances numbers in non-tested cases cells were added up across all cells, allowing a corrected total estimate for this group. Cases with missing values in age, sex or number of treatments were not considered. As shown, the described approach is conceptually akin to standardization. Some methodological comments are included in next chapter, acting as contexts for results.
3. Results
3.1. From Having Tuberculosis to Being Identified as a MDR-TB Case
Figure 3 is represents the conditional probability chain of a patient to become identified as a MDR-TB case; the number of patients known (in bold) or estimated, in 2000-2009, is shown. Depending on how the global proportion of MDR-TB cases was calculated (different scenarios and denominators), a diversity of probabilities of being resistant among notified cases could be estimated, from exactly the same count of resistants (390). This quantifies the diagram in Figure 1.
The first node’s dimension (58,600) was estimated based on the Portuguese notification rate (87%) made by WHO [26] and considering all Portuguese cases notified in 2000-2009 (50,982). Although 68% of positive cultures were tested for MDR-TB, out of the total notified cases only 32.2% were actually tested for MDR-TB (16,396 cases). Even more, the same proportion of cases (32.2%) was tested for H, R, and H∩R.
3.2. Drug Susceptibility Testing (DST) Frequencies
Testing frequencies for H, R, Z, E and S had much greater magnitudes as compared to testing for second-line antibiotics (Figure 4).
3.3. Estimating Multi Drug Resistances
Classical Approach (1)
The classical approach takes prevalence in tested cases as a convenient proxy of the prevalence in all cases. Considering that 390 MDR-TB cases were identified among the 16396 tested cases, a global estimated percentage of 2.38% of MDR-TB was obtained (equal prevalence in non-tested cases assumed and not considering the effects of possible factors that may promote or prevent testing).
The Correcting Method (2)
The principle is that, if the group of tested and the group of non-tested differ in characteristics that may predict testing practices and, possibly, resistance to antibiotics, then the previously calculated proportion must be corrected for such differences. As a result of logistic regressions, Figure 5 and Figure 6 show that the exposure to some factors was, in fact, likely to predict different probabilities of being tested, in concordance with Figure 1.
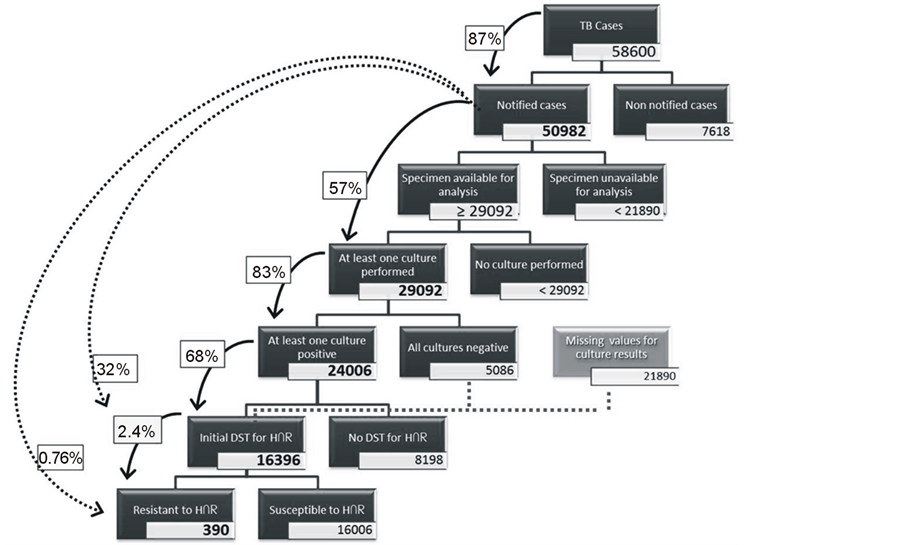
Figure 3. Tentative conditional probability chain, from having Tuberculosis to being identified as a MDR-TB case (Portugal, 2000-2009; counts [bold], estimates and %). Model based on SVIG-TB.
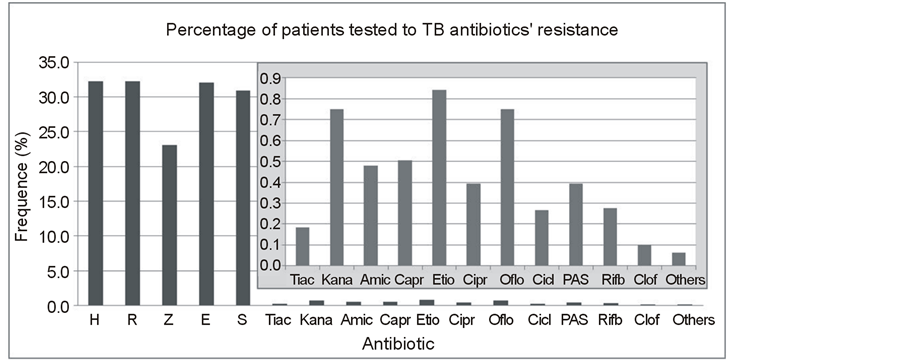
Figure 4. Frequencies (%) of testing to each antibiotic, among total TB cases (2nd line antibiotics zoomed). Legend: Isoniazid (H), Rifampicin (R), Pyrazinamide (Z), Ethambutol (E), Streptomycin (S), Thiacetazone (Tiac), Kanamycin (Kana), Amikacin (Amic), Capreomycin (Capr), Ethionamide (Etio), Ciprofloxacin (Cipr), Ofloxacin (Oflo), Cycloserine (Cicl), Para-Amino Salicylic acid (PAS), Rifabutin (Rifb) and Clofazimine (Clof).
Being male looked a predictor for increased initial DST undertaking (OR = 1.51; CI95%: 1.43 - 1.60), similarly to alcoholic patients (OR = 1.61; CI95%: 1.50 - 1.74). Having at least one previous treatment was also a predicting factor for testing (OR = 1.40; CI95%: 1.29 - 1.53). Interestingly, foreigners were almost as likely to be tested as native patients (OR = 1.11; CI95%: 1.03 - 1.20); and drug addicts (OR = 0.91; CI95%: 0.83 - 0.99) and HIV positive (OR = 0.66; CI95%: 0.61 - 0.71) patients seemed less likely to be tested than non-drug addicts and HIV negative patients, respectively. Age was an important predictor for testing, with a heterogeneous impact (Figure 6).

Figure 5. Odds Ratios for some factors predicting MDR-TB testing, crude (Δ) and adjusted to all variables analyzed ( ), and 95% CI, depending on characteristics of TB patients. Portugal, 2000-2009.
), and 95% CI, depending on characteristics of TB patients. Portugal, 2000-2009.
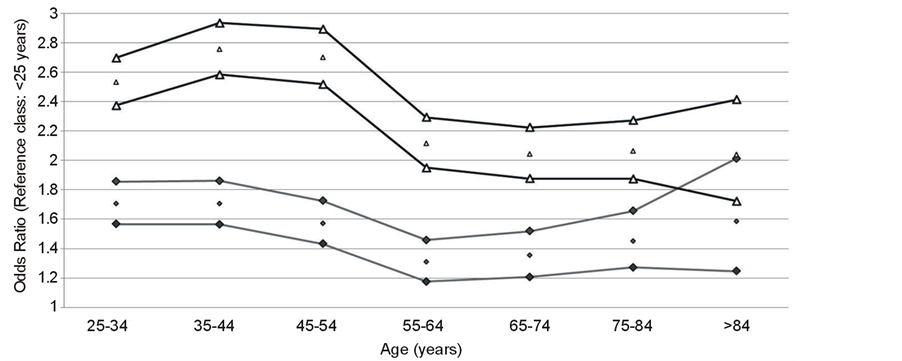
Figure 6. Odds Ratios for age groups predicting MDR-TB testing of TB patients, Portugal, 2000-2009, crude (Δ) and adjusted ( ), and 95% CI; reference class: <25 years.
), and 95% CI; reference class: <25 years.
All the studied predicting dimensions did seem to influence the probability for cases to be tested to H∩R anyhow, and in various degrees. Given the different exposure structures in tested and non-tested, the correcting estimation method was essayed, as follows.
Table 1 summarizes results of this approach in the Portuguese context (2000-2009), according to different predictor combinations. The set of factors selected for elaborating Figure 2 is underlined. Factors with major proportions of cases excluded because of missing values were less appropriate for correction, as these might produce some kind of uncontrolled bias—missing data may be associated with one or several predictors.
Depending on the factors considered, resistances’ estimates in non-tested varied, and were different from the non-corrected ones, in the total number of notified cases. E.g., if the proportion of resistances was corrected for age and sex, 50,755 notified cases were included; however, if the correction was also made for HIV, only 30,000 cases could be included. This happened because the HIV variable had 40.9% of cases with missing values; these couldn’t enter the estimation procedure.
The summary assessment of both the construct validity and functionality of the described correcting model indicated it’s appropriateness for the purpose and, furthermore, suitability for other analogous situations.
As Table 1 shows, correcting estimates yielded slightly lower prevalence values, as expected, meaning that tested patients had, in fact, a higher risk of being MDR-TB cases, in the Portuguese setting. From all correction criteria presented, that one combining sex, age, retreatment and country of origin was considered more accurate (bold) than the others, as it included 4 variables with low missing values numbers (0.68%).
Table 1. Estimations of resistant cases and prevalences in non-tested and in all cases, as a function of different sets of factors values (strata) predicting testing for MDR-TB.
aTested + non-tested. bEstimated by correcting method. cClassical Approach; Legend: Ret—Retreatment, Alc—alcholism, Drug—Drug abuse.
4. Discussion
To know the proportion of MDR-TB cases involves a complex decision chain. Although 68% of positive cultures were tested for DST among notified cases, only 32% of these were actually tested for H∩R, in 2000-2009. This probably happens because: 1) notified cases need to be able to provide a biologic product for testing (usually sputum; but it can be other specimen) and it must be submitted to at least one culture and its result must be positive, so that a DST is possible; 2) depending on the physician’s options and on healthcare facilities, smear positive cases may not be tested for any antibiotic. Admitting that medical care options play the principal role in the decision of who is tested, testing preferences found were rather coherent with predicting factors for unsuccess, as known from the literature.
This essay is focused on MDR-TB cases, because of their importance in TB control; but results of tests to both antibiotics, as shown in Figure 4, need to be interpreted in the appropriate practical context. Frequencies presented in Figure 4 are quite expected, but some concern about the comparability of resistances proportions between first-line and second-line antibiotics must be raised; tested cases are the denominators of resistance proportions, and second-line antibiotics are far less tested; therefore, proportions are much less accurate here. Moreover, DST technology reliability is not considered in estimations, but it depends on the antibiotic to be tested [20] and may also vary in space and time. Meanwhile, discussing the interest of these “in vitro” tests for the field control of TB is out of the scope of this paper, but “in vivo” antibiotics synergy in each combination pack and with the patient’s self-defense mechanisms should not be devalued.
The conditional probability chain (Figure 3) was elaborated from SVIG-TB data. This doesn’t allow a distinction between cases that weren’t tested because there wasn’t a specimen available, from cases that weren’t tested for other reasons. Therefore, all cases were included in the regression, although only patients with both an available biologic product for analysis and a positive culture should have been included; these were the only really liable to be tested. Moreover, it is not possible to assess whether the decision for testing was made exclusively by the physician, or whether the health institution or laboratory staff was also involved.
In the presented approach, as mentioned, all non-tested patients were included as “controls” for tested, because: 1) the resistance phenomenon and a specimen collection for testing could virtually occur in any of them, with a variable degree of invasiveness; and 2) a narrower selection of “controls” would raise additional hampering small numbers difficulties. In all alternatives, the so complex web of relationships found and the mentioned uncertainty could facilitate possible confounding effects of the very testing predictors on future resistance proportions, as such factors may also explain either the real availability of a specimen for culture, or a positive culture [27] . Therefore, in the context of the present essay, tested and non-tested may be taken as comparable enough for the purpose and caution expressed about this issue outlines the risks of this assumption appropriately. Particularly, if “predictors for testing” have a marked low prevalence in the (unknown) patients really not providing a specimen for culture, the weight of these patients as “controls” will tend to increase the final odds ratio estimates. Anyway, the resistance prevalence ends up being generalized to all notified cases, for control purposes, which is a rather blind decision.
Measurements validity regarding studied variables closely depended on the original data on associated practices. E.g., zooming on HIV infection status, a similar practice of selective diagnostic testing may have occurred, representing another source of bias: HIV-positive patients seemed less likely of being tested for H∩R than HIV-negatives, due to the fact that clinicians may tend to decide directly and blindly for prescribing second-line antibiotics to HIV-positive patients.
As previously known [28] , selected factors predict testing practices and these also change throughout time. Studies should focus on short periods of time (e.g. biannual) ideally, as a good monitoring, and face possible small numbers problems.
Estimating resistances in non-tested cases, allowing for predictors of testing, means that tested and non-tested only differ in the characteristics studied, which may not be true. Ideally, all characteristics previously established in literature as predictors for MDR-TB should be considered. In this study, previous contact with a MDR-TB case, a characteristic likely to suggest MDR-TB testing, was not included due to unavailability of such data. However, this characteristic in a country such Portugal would probably not affect the results, because almost all patients known to be in contact with MDR-TB are very likely to be tested. A qualitative study regarding determinants for testing could be useful for further studies.
Also the presence of missing values is an important limitation and careful decisions must be taken. In the case of low percentages of missing values (<10% as an indicative and subjective value), more risk factors could be considered for adjustment. In other situations (≥10%), it could lead to a loss of considerable number of cases and could introduce further bias. Therefore, theoretically, this approach should embrace the greatest number of identified variables and reject those with high numbers of missing values, simultaneously. Complementary to the missing data problem, the quality of data is another issue that should be considered in the variables’ choice.
Odds ratios for HIV must be cautiously valued, as a too high a proportion of cases was excluded (missing values = 40%). Variables such as drug addiction and alcoholism have less missing values cases (near 10%), but their measurement is very subjective and may be heterogeneously interpreted by medical staff. Corrections for age, sex, retreatment and country of origin (all with few missing values cases and higher odds ratio values) seemed, in this specific situation, an appropriate choice.
In the proposed method, the similarity of resistance proportions in corresponding strata, in tested and non-tested, was assumed. Lower global resistance proportions would be obtained if smaller resistance prevalence were assumed, with the same correction criteria regarding predictors for testing. Our more conservative option in this essay is prudent, in the absence of further local appropriate information.
All methodological limitations don’t wipe the evidence that selection criteria for testing, in Portugal, artificially increase the global resistance prevalence value slightly, when a non-corrected calculation is used. But in other contexts where laboratory facilities are less available, these criteria may act more intensely, generating major differences between tested and non-tested structures and resulting in a larger distortion.
The simplicity, the intuitiveness and the internal coherence of the essayed method make it, in fact, suitable as a solution for similar estimation problems, in analogous situations.
5. Conclusions
From the occurrence of a new case in the population, until finding a resistance in a notified case, a complex chain of conditional events happened.
They differed in several degrees and different ways regarding studied predicting factors for testing: sex, age, drug abuse, alcohol abuse, country of origin, number of previous treatments, HIV co-infection.
Generalizing DST results from tested patients to non-tested straightforwardly can lead to a relevant distortion of the global resistance prevalence estimate, when some patients’ characteristics either increase or decrease DST undertaking practice. This can be a major shortcoming, when using the conventional estimation approach.
In the Portuguese setting, crude (2.38%) and corrected (2.14%) (for age, sex, country and retreatment) MDR-TB prevalences estimated for 2000-2009 were rather similar; however, in other settings, where patients’ characteristics are even more determinant in the decision of testing, thus making tested and non-tested differ more drastically, those estimates can be much distinct, resulting in major implications for monitoring and decision making.
The method now developed and essayed for resistance prevalence correction is a coherent, simple and intuitive approach, easy to replicate when the required input information is available and appropriate assumptions are made. It is able to facilitate the interpretation of such prevalence and to improve consequent decisions. Method’s features make it suitable, by analogy, for improving proportions estimation in other similar situations.
Acknowledgements
The authors would like to thank to the coordinators of the National Program for Tuberculosis Control, for kindly allowing us to use data on Tuberculosis Surveillance. This study was supported by Fundação para Ciência e Tecnologia, within the research project PTDC/SAU-SAP/116950/2010 and by Lilly Portugal—Produtos Farmacêuticos, Lda.
References
- WHO (2013) Global Tuberculosis Report 2013. WHO, Geneva.
- Maher, D. and Raviglione M. (2005) Global Epidemiology of Tuberculosis. Clinics in Chest Medicine, 26, 167-182. http://dx.doi.org/10.1016/j.ccm.2005.02.009
- Duarte, R. and Diniz, A. (2013) Programa Nacional de Luta Contra a Tuberculose Ponto da Situação Epidemiológica e de Desempenho (dados provisórios) . Directorate-General of Health, Lisbon.
- Briz, T., Nunes, C., Alves, J. and Santos, O. (2009) O controlo da tuberculose em Portugal : Uma apreciação crítica epidemiológica global . Revista Portuguesa de Saúde Pública, 27, 19-54.
- Aziz, M.A., Wright, A., Laszlo, A., Muynck, A., Portaels, F., Van Deun, A., Wells, C., Nunn, P., Blanc, L. and Raviglione, M. (2006) Epidemiology of Antituberculosis Drug Resistance (the Global Project on Anti-Tuberculosis Drug Resistance Surveillance): An Updated Analysis . Lancet, 368, 2142-2154. http://dx.doi.org/10.1016/S0140-6736(06)69863-2
- WHO (2003) Guidelines for Surveillance of Drug Resistance in Tuberculosis . 4th Edition, WHO, Geneva.
- Cohn, D.L., Bustreo, F. and Raviglione, M.C. (1994) Drug-Resistant Tuberculosis : Review of the Worldwide Situation and the WHO/IUATLD Global Surveillance Project . 121-130.
- Nathanson, E., Nunn, P., Uplekar, M., Floyd, K., Jaramillo, E., Lönnroth, K., Weil, D. and Raviglione M. (2010) MDR Tuberculosis —Critical Steps for Prevention and Control. The New England Journal of Medicine, 363, 1050- 1058. http://dx.doi.org/10.1056/NEJMra0908076
- Mukherjee, J.S., Rich, M.L., Socci, A.R., Joseph, J.K., Virú, F.A., Shin, S.S., Furin, J.J., Becerra, M.C., Barry, D.J., Kim, J.Y., Bayona, J., Farmer, P., Smith Fawzi, M.C. and Seung K.J. (2004) Programmes and Principles in Treatment of Multidrug-Resistant Tuberculosis. Lancet, 363, 474-481. http://dx.doi.org/10.1016/S0140-6736(04)15496-2
- Crofton, J. and Mitchison, D. (1948) Streptomycin Resistance in Tuberculosis. British Medical Journal, 4588, 1009- 1015. http://dx.doi.org/10.1136/bmj.2.4588.1009
- Kochi, A., Vareldzis, B. and Styblo, K. (1993) Multidrug-Resistant Tuberculosis and Its Control . Research in Microbiology, 73, 219-224.
- Stop TB Partnership (2006) The Global Plan to Stop TB . WHO 2006-2015, Geneva.
- Faustini, A., Hall, A.J. and Perucci, A.C. (2006) Risk Factors for Multidrug Resistant Tuberculosis in Europe: A Systematic Review . Thorax, 61,158-163. http://dx.doi.org/10.1136/thx.2005.045963
- Su, W.J., Feng, J.Y., Huang, C.C. and Perng, R.P. (2008) Increasing Drug Resistance of Mycobacterium tuberculosis Isolates in a Medical Center in Northern Taiwan . Journal of the Formosan Medical Association, 107, 259-264. http://dx.doi.org/10.1016/S0929-6646(08)60145-X
- WHO (2007) Multidrug and Extensively Drug-Resistant TB (M/XDR-TB) 2010 . Global Report on Surveillance and Response. WHO, Geneva.
- Nunes, C. (2007) Tuberculosis Incidence in Portugal: Spatiotemporal Clustering . International Journal of Health Geographics, 6, 30. http://dx.doi.org/10.1186/1476-072X-6-30
- Antunes, A. (2011) Programa nacional de luta contra a tuberculose . Ponto de situação 2011. Directorate-General of Health, Lisbon.
- DGS (2012) Programa nacional de luta contra a tuberculose . Ponto de situação 2012, DGS, Lisbon.
- Antunes, M.L., Aleixo-Dias, J., Antunes, A.F., Pereira, M.F., Raymundo, E. and Rodrigues, M.F. (2000) Anti-Tuberculosis Drug Resistance in Portugal. The International Journal of Tuberculosis and Lung Disease, 4, 223-231.
- Kim, S.J. (2005) Drug-Susceptibility Testing in Tuberculosis: Methods and Reliability of Results . The European Respiratory Journal, 25, 564-569. http://dx.doi.org/10.1183/09031936.05.00111304
- Frieden, T. (2004) TOMAN’S TUBERCULOSIS: Case Detection, Treatment and Monitoring—Questions and Answers . 2nd Edition, Geneva.
- WHO (2008) Stop TB Policy Paper: Contributing to Health System Strengthening. Guiding Principles for National Tuberculosis Programes . WHO, Geneva.
- Arghya, R. (2012) The Methodology of Sampling and Purposive Sampling . Munich.
- Sharp M. and Corp, D. (2012) Tuberculosis. The Merck Manual for Health Professionals. http://www.merckmanuals.com/professional/infectious_diseases/mycobacteria/tuberculosis_tb.html#v1010771 http://dx.doi.org/10.1016/S0140-6736(82)91579-3
- Bernadt, M.W., Taylor, C., Mumford, J., Smith, B. and Murray, R.M. (1982) Comparison of Questionnaire and Laboratory Tests in the Detection of Excessive Drinking and Alcoholism. The Lancet, 319, 325-328.
- WHO (2013) Tuberculosis Country Profiles . WHO, Geneva. http://www.who.int/tb/country/data/profiles/en/index.html
- Cohen, T., Colijn, C., Finklea, B., Wright, A., Zignol, M., Pym, A. and Murray, M. (2008) Are Survey-Based Estimates of the Burden of Drug Resistant TB Too Low? Insight from a Simulation Study. PloS One, 3, e2363. http://dx.doi.org/10.1371/journal.pone.0002363
- Briz, T., Areias, C., Filipe, P. and Nunes, C. (2012) Tuberculosis Control in Portugal and Resistances to Antibiotics: How to Interpret Multirresistance Prevalences in the Context of Real Testing Practices? European Journal of Epidemiology, 27, OC 2.2.2.


