American Journal of Computational Mathematics
Vol.06 No.03(2016), Article ID:70399,13 pages
10.4236/ajcm.2016.63023
Concentration Wave for a Class of Reaction Chromatography System with Pulse Injections
Jing Zhang1, Maofei Shao1, Tao Pan2*
1Department of Mathematics, Jinan University, Guangzhou, China
2Department of Optoelectronic Engineering, Jinan University, Guangzhou, China

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 July 2016; accepted 3 September 2016; published 6 September 2016
ABSTRACT
By using fluid dynamics theory with the effects of adsorption and reaction, the chromatography model with a reaction A ® B was established as a system of two hyperbolic partial differential equations (PDE’s). In some practical situations, the reaction chromatography model was simplified a semi-coupled system of two linear hyperbolic PDE’s. In which, the reactant concentration wave model was the initial-boundary value problem of a self-closed hyperbolic PDE, while the resultant concentration wave model was the initial-boundary value problem of hyperbolic PDE coupling reactant concentration. The general explicit expressions for the concentration wave of the reactants and resultants were derived by Laplace transform. The d-pulse and wide pulse injections were taken as the examples to discuss detailedly, and then the stability analysis between the resultant solutions of the two modes of pulse injection was further discussed. It was significant for further analysis of chromatography, optimizing chromatographic separation, determining the physical and chemical characters.
Keywords:
Reaction Chromatography Model, Hyperbolic Partial Differential Equations, Initial-Boundary Problem, Stability Analysis

1. Introduction
With the appearance of diverse production chromatography (such as the reaction chromatography), the chromato- graphy technology has been widely applied in chemistry, chemical engineering, biological engineering and pharmaceutical engineering, etc., while the demand of chromatography theory is increasing higher. The relation- ships among the chromatographic input-output and the system conditions play the very important role in chromatography model [1] - [6] .
In fact, the mathematical model of chromatography system is a initial-boundary value problem of hyperbolic partial differential equations system [7] - [11] , which is hard and challenging mathematics problem to chromato- graphy scientists. In the other hand, the practical application and demand for chromatography is also difficult to understand deeply by mathematicians. The relative works of partial differential equations in the practical chromatography are still not enough.
If the chromatographic process contains reactions, it is labeled as reaction chromatography. An important example is the catalyst for the column packing, accompanied the catalytic [2] - [6] in the adsorption process, and the isomerization reaction is the common situation.
In this paper, a chromatography model with a reaction 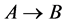 was established, which is a initial-boundary value problem for the semi-coupled system of two linear hyperbolic partial differential equations. Then the general explicit expressions of concentration waves for reactant and resultant were derived using Laplace transform. It was significant for further analysis between input and output of chromatography, optimizing chromatographic separation, determining the physical and chemical characters. Finally, the d-pulse and wide pulse injections were taken as the examples to discuss detailedly, and then the stability analysis between the resultant solutions of the two modes of pulse injection was further discussed. The results provided proper theory models for further chromatographic data analysis.
was established, which is a initial-boundary value problem for the semi-coupled system of two linear hyperbolic partial differential equations. Then the general explicit expressions of concentration waves for reactant and resultant were derived using Laplace transform. It was significant for further analysis between input and output of chromatography, optimizing chromatographic separation, determining the physical and chemical characters. Finally, the d-pulse and wide pulse injections were taken as the examples to discuss detailedly, and then the stability analysis between the resultant solutions of the two modes of pulse injection was further discussed. The results provided proper theory models for further chromatographic data analysis.
2. Reaction Chromatography Model
Set the concentrations of the reactant A and the resultant B in the mobile phase and in the stationary phase as 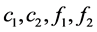 respectively. Reaction rate was
respectively. Reaction rate was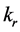 . And the linear velocity of the mobile phase was u. The volume shares in chromatographic column in the mobile phase and in the stationary phase as
. And the linear velocity of the mobile phase was u. The volume shares in chromatographic column in the mobile phase and in the stationary phase as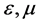 , respectively.
, respectively.
Denoted that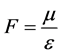 , then the mass conservation equations between reactant and resultant in the catalytic
, then the mass conservation equations between reactant and resultant in the catalytic
chromatographic process was shown as below:
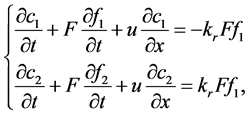 (1)
(1)
where, 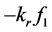 was the reactant reduction rate, and
was the reactant reduction rate, and 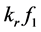 was resultant increase rate,
was resultant increase rate, 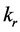 was the coefficient of reaction rate. According to Langmuir type adsorption isotherms,
was the coefficient of reaction rate. According to Langmuir type adsorption isotherms, 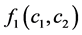 and
and 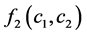 satisfied for:
satisfied for:
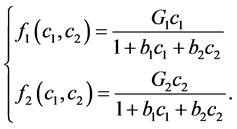 (2)
(2)
The concentration wave Equation (1) were a system of two nonlinear hyperbolic partial differential equations, which was a hard mathematical problem. But in some practical situations, the problem can be simplified [2] . Assume 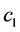 was small, or the adsorption coefficient
was small, or the adsorption coefficient 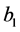 was small, that was,
was small, that was,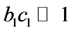 . While considering the assumed reaction rate
. While considering the assumed reaction rate 




and denoted concretely:

they were positive constant, thus Equation (1) can be simplified to the following semi-coupled system of two linear hyperbolic partial differential equations. In which, the reactant concentration wave model was the initial- boundary value problem of a self-closed hyperbolic partial differential equations, while the resultant con- centration wave model was the initial boundary value problem of hyperbolic partial differential equations coupling reactant concentration.

Chromatographic process started from the boundary, and there were many types of the boundary conditions, such as the injection methods of d-pulse, wide pulse, head-on, etc.; whose corresponding boundary condition were not zero. The initial state of chromatography columns were typically empty, that the initial conditions corresponding to 0. However, in practical problems, there were some important chromatograph whose corre- sponding initial conditions is not zero, such as simulated moving bed chromatography. Therefore, it is necessary to study the general initial-boundary value problem with both the initial and boundary values were not 0. That was, 


where, 


3. Explicit Solution of Concentration Wave
Firstly, solved the initial-boundary value problem (6) for concentration wave of of reactant
it follows from (6) that

Then solved the ordinary differential Equation (8) about
and
Since

and
That is to say,

To sum (9) and (10) up,

Then solved the initial-boundary value problem (7) for the concentration wave of resultant
The above problem (7) satisfied the following ordinary differential equation:

Solved the ordinary differential Equation (12) about
Hence, we got
Since

and
where

Meanwhile, we had
and

To sum (13), (14) and (15) up,

Using the expression (11) of 



In the case of

In the case of


In the case of


Particularly, when the initial-boundary problem (6) and (7) satisfied the following conditions
the explicit solution of reactant and resultant concentration wave 
Following (11), we had

According to the expressions (17), (18) and (19), we had the explicit solution expressions of 
When

When

When

4. Solutions and Stability for d-Pulse and Wide Pulse Injections
In this section, we derived the solutions of reactant and resultant concentration waves in wide pulse and d-pulse injections detailedly. And the stability analysis between the resultant solutions of the two modes of pulse injection was further discussed.
4.1. d-Pulse Injection
Chromatographic process started from the boundary, and there were many types of the boundary conditions, such as the methods of d-pulse, wide pulse, head-on, etc; whose corresponding boundary condition was not zero. Where, d-pulse and wide pulse were the most common way of chromatography injection method. Firstly, initial state of chromatography column in the d-pulse method, which injection function was a kind of d-function, was typically empty. So in the case of d-Pulse, 

where k is a constant represented the injection size, which is equal to 
The solution of concentration wave for reactant was obtained by Laplace transform as similar with Section 3. The concentration wave corresponding to d-pulse injection of reactant and resultant can be expressed as follows.

If there was no reaction terms, that was, 

As for the solution of concentration wave for resultant, the initial and boundary values were both 0. From the expression (21), (22) and (23), we had the explicit solution expressions of
When

It was equivalent to
When

When

4.2. Wide Pulse Injection
Wide pulse was the another most common way of chromatography injection method, its initial state of chromato- graphy column was typically empty, so the initial condition was the follows,
The corresponding injection function was given as follows,

where, 

Similarly, we had the explicit solution expressions of 


When

When

When

4.3. Stability Analysis between Wide Pulse and d-Pulse Injections
Note that, the boundary condition in wide pulse injection tended to the condition in d-pulse injection. We also showed that the mentioned limit relationship was still valid for the solutions in the two modes of pulse injection. The main result of this work is the following theorem:
Theorem 1. If 

Proof. 1) When


and when


By arbitrariness of

which was converging to the solution (27) in d-pulse injection.
2) When
In the case of

In the case of

For any fixed


noted to:

Furthermore, for any fixed
a) When
b) When


and
c) When


To sum up,

3) When
In the case of

In the case of

For any fixed


noted to:

and for any
i) When
ii) When


iii) When


By arbitrariness of 


By (35), (39) and (43), we can conclude that this Theorem is true. □
5. Conclusion
The chromatography model with a reaction 
Acknowledgements
This work was supported by National Natural Science Foundation of China (No. 21312045) and Science and Technology Project of Guangdong Province of China (No. 2014A020213016).
Cite this paper
Jing Zhang,Maofei Shao,Tao Pan, (2016) Concentration Wave for a Class of Reaction Chromatography System with Pulse Injections. American Journal of Computational Mathematics,06,224-236. doi: 10.4236/ajcm.2016.63023
References
- 1. Pan, T., Liu, H. and Nishihara, K. (2002) Asymptotic Behavior of a One-Dimensional Compressible Viscous Gas with Free Boundary. SIAM Journal on Mathematical Analysis, 34, 273-291.
http://dx.doi.org/10.1137/S0036141001385745 - 2. Pan, T. and Liu, H. (2002) Asymptotic Behaviors of the Solution to an Initial-boundary Value Problem for Scalar Viscous Conservation Laws. Applied Mathematics Letters, 15, 727-734.
http://dx.doi.org/10.1016/S0893-9659(02)00034-4 - 3. Pan, T. and Jiu, Q. (1999) Asymptotic Behavior for Solution of the Scalar Viscous Conservation Laws in the Bounded Interval Corresponding to Rarefaction Waves. Progress in Natural Science, 9, 948-952.
- 4. Pan, T, Liu, H. and Nishihara, K. (1999) Asymptotic Stability of the Rarefaction Wave of a One Dimensional Model System for Compressible Viscous Gas with Boundary. Japan Journal Industrial Applied Mathematics, 16, 431-441.
http://dx.doi.org/10.1007/BF03167367 - 5. Pan, T. and Lin, L. (1995) The Global Solution of the Scalar Nonconvex Conservation Laws with Boundary Condition. Journal of Partial Differential Equations, 8, 371-383.
- 6. Qamar, S., Bibi, S., Khan, F.U., Shah, M., Javeed, S. and Seidel-Morgenstern, A. (2014) Irreversible and Reversible Reactions in a Liquid Chromatographic Column: Analytical Solutions and Moment Analysis. Industrial & Engineering Chemistry Research, 53, 2461-2472.
http://dx.doi.org/10.1021/ie403645w - 7. Bibi, S., Qamar, S. and Seidel-Morgenstern, A. (2015) Irreversible and Reversible Reactive Chromatography: Analytical Solutions and Moment Analysis for Rectangular Pulse Injections. Journal of chromatography, 1385, 49-62.
http://dx.doi.org/10.1016/j.chroma.2015.01.065 - 8. Qamar, S., Perveen, S. and Seidel-Morgenstern, A. (2016) Analysis of a Two-Dimensional Nonequilibrium Model of Linear Reactive Chromatography Considering Irreversible and Reversible Reactions. Industrial & Engineering Chemistry Research, 55, 2471-2482.
http://dx.doi.org/10.1021/acs.iecr.5b04714 - 9. Lin, B., Song, F. and Guiochon, G. (2003) Analytical Solution of Ideal Nonlinear Model of Reaction Chromatography for a Reaction and a Parabolic Isotherm. Journal of Chromatography A, 1003, 91-100.
http://dx.doi.org/10.1016/S0021-9673(03)00656-3 - 10. Lin, B. (2004) Guiding of the Chromatography Model Theory. Science Press, Beijing.
- 11. Guiochon, G., Ghodbane, S., Golshan-Shirazi, S., et al. (1989) Non-Linear Chromatography: Recent Theoretical and Experimental Results. Talanta, 36, 19-33.
http://dx.doi.org/10.1016/0039-9140(89)80079-7
NOTES
*Corresponding author.


































