Received 6 April 2016; accepted 6 June 2016; published 9 June 2016

ABSTRACT

In this article, we establish a common fixed point theorem satisfying integral type contractive condition for two pairs of weakly compatible mappings with E. A. property and also generalize Theorem (2) of B.E. Rhoades [1] in dislocated metric space.

Keywords:

Dislocated Metric, Weakly Compatible Maps, Common Fixed Point

1. Introduction

In 1986, S. G. Matthews [2] introduced some concepts of metric domains in the context of domain theory. In 2000, P. Hitzler and A.K. Seda [3] introduced the concept of dislocated topology where the initiation of dis- located metric space was appeared. Since then, many authors have established fixed point theorems in dislocated metric space. In the literature, one can find many interesting recent articles in the field of dislocated metric space (see for examples [4] - [10] ).

The study of fixed point theorems of mappings satisfying contractive conditions of integral type has been a very interesting field of research activity after the establishment of a theorem by A. Branciari [11] . The purpose of this article is to establish a common fixed point theorem for two pairs weakly compatible mappings with E. A. property and to generalize a result of B.E. Rhoades [1] in dislocated metric space.

2. Preliminaries

We start with the following definitions, lemmas and theorems.

Definition 1 [3] Let X be a non empty set and let 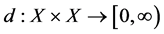be a function satisfying the following conditions:

1.

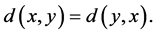
2. 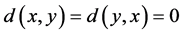implies

3. 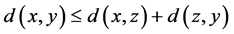for all.

Then d is called dislocated metric (or d-metric) on X and the pair 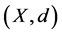is called the dislocated metric space (or d-metric space).

Definition 2 [3] A sequence 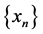in a d-metric space is called a Cauchy sequence if for given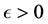, there corresponds 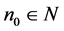such that for all, we have.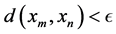

Definition 3 [3] A sequence in d-metric space converges with respect to d (or in d) if there exists such that 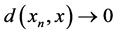as

Definition 4 [3] A d-metric space is called complete if every Cauchy sequence in it is convergent with respect to d.

Lemma 1 [3] Limits in a d-metric space are unique.

Definition 5 Let A and S be two self mappings on a set X. If for some, then x is called coincidence point of A and S.

Definition 6 [12] Let A and S be mappings from a metric space into itself. Then, A and S are said to be weakly compatible if they commute at their coincident point; that is, for some implies

Definition 7 [13] Let A and S be two self mappings defined on a metric space. We say that the mappings A and S satisfy (E. A.) property if there exists a sequence such that

for some

3. Main Results

Now we establish a common fixed point theorem for two pairs of weakly compatible mappings using E. A. pro- perty.

Theorem 1 Let (X, d) be a dislocated metric space. Let satisfying the following con- ditions

(1)

(2)

where

is a Lebesgue integrable mapping which is summable, non-negative and such that

(3)

(4)

1. The pairs or satisfy E. A. property.

2. The pairs and are weakly compatible.

if T(X) is closed then

1) the maps A and T have a coincidence point.

2 the maps B and S have a coincidence point.

3) the maps A, B, S and T have an unique common fixed point.

Proof. Assume that the pair satisfy E.A. property, so there exists a sequence such that

(5)

for some. Since, so there exists a sequence such that. Hence,

(6)

From condition (2) we have

(7)

where

Taking limit as we get

(8)

Since

Hence we have

which is a contradiction, since. Hence,. Now we have

Assume is closed, then there exits such that. We claim that. Now from condition (2)

(9)

where

Since

So, taking limit as in (9), We conclude that

(10)

which is a contradiction. Hence. Now we have

(11)

This proves that v is the coincidence point of.

Again, since so there exists such that

Now we claim that. From condition (2)

where

Since

So if or we get the contradiction, since

or

Hence,

Therefore,.

This represents that w is the coincidence point of the maps B and S.

Hence,

Since the pairs and are weakly compatible so,

We claim. From condition (2)

where

Since

So if or or we get the contradiction. Since,

or

Hence,

Therefore,. Similary,. Hence,. This represents that is the common fixed point of the mappings and T.

Uniqueness:

If possible, let be other common fixed point of the mappings, then by the condition (2)

(12)

where

Since

So if or or we get the contradiction, since

or

or

Hence, This establishes the uniqueness of the common fixed point of four mappings.

Now we have the following corollaries:

If we take T = S in Theorem (1) the we obtain the following corollary

Corollary 1 Let (X,d) be a dislocated metric space. Let satisfying the following conditions

where

is a Lebesgue integrable mapping which is summable, non-negative and such that

1. The pairs or satisfy E. A. property.

2. The pairs and are weakly compatible.

if S(X) is closed then

1) the maps A and S have a coincidence point

2) the maps B and S have a coincidence point

3) the maps A, B and S have an unique common fixed point.

If we take B = A in Theorem (1) we obtain the following corollary.

Corollary 2 Let (X, d) be a dislocated metric space. Let satisfying the following conditions

where

is a Lebesgue integrable mapping which is summable, non-negative and such that

(13)

1. The pairs or satisfy E. A. property.

2. The pairs and are weakly compatible.

if T(X) is closed then

1) the maps A and T have a coincidence point.

2) the maps A and S have a coincidence point.

3) the maps A, S and T have an unique common fixed point.

If we take T = S and B = A in Theorem (1) then we obtain the following corollary

Corollary 3 Let (X, d) be a dislocated metric space. Let satisfying the following conditions

where

is a Lebesgue integrable mapping which is summable, non-negative and such that

1. The pairs satisfy E. A. property.

2. The pair is weakly compatible.

if S(X) is closed then maps A and S have a unique common fixed point.

If we put S = T = I (Identity map) then we obtain the following corollary.

Corollary 4 Let (X, d) be a dislocated metric space. Let satisfying the following conditions

(14)

(15)

where

is a Lebesgue integrable mapping which is summable, non-negative and such that

(16)

(17)

if the pair (A, B) satisfy E.A. property and are weakly compatible then the maps A and B have an unique common fixed point.

Remarks: Our result extends the result of [14] .

Now we establish a fixed point theorem which generalize Theorem (2) of B. E. Rhoades [1] .

Theorem 2 Let (X, d) be a complete dislocated metric space, , be a mapping such

that for each

(18)

where

(19)

and

is a lebesgue integrable mapping which is summable , non negative and such that

(20)

for each, then f has a unique fixed point, moreover for each

Proof. Let and define , then from (18)

(21)

now by (19)

But,

and similarly we can obtain,

Hence

Therefore by (21)

Similarly we can obtain,

Hence

Now taking limit as we get

(22)

by (20)

Now we claim that is a Cauchy sequence.

If possible let is not a Cauchy sequence, then there exists a real number and subsequences and such that and

(23)

Using (19) we have,

(24)

Now using (22)

(25)

Since by triangle inequality and (23)

Hence

(26)

and

(27)

Similarly

(28)

Hence, from (20), (23), (24), (25), (26), (27) and (28)

which is a contradiction. Hence is a Cauchy sequence. Hence there exists a point such that the sequence and its subsequences converge to z.

From the condition (18)

Now taking limit as we obtain

which implies

So from the relation (20) we obtain

Uniqueness:

Let z and w two fixed point fixed points of the function f.

Applying condition (19) we obtain

If maximum of the given expression in the set is then

which is a contradiction, since. Similarly for other cases also we get the contradiction. Hence z = w. This completes the proof of the theorem.

Cite this paper

P. M. Geethu Krishnan,A. Sobha,Mini P. Balakrishnan,R. Sumangala,Dinesh Panthi,Panda Sumati Kumari, (2016) Some Integral Type Fixed Point Theorems in Dislocated Metric Space. American Journal of Computational Mathematics,06,88-97. doi: 10.4236/ajcm.2016.62010

References