American Journal of Computational Mathematics
Vol.06 No.01(2016), Article ID:65171,5 pages
10.4236/ajcm.2016.61004
An Integer Coding Based Optimization Model for Queen Problems
Nengfa Hu
Department of Computer Science and Engineering, Hanshan Normal University, Chaozhou, China

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 March 2016; accepted 27 March 2016; published 30 March 2016
ABSTRACT
Queen problems are unstructured problems, whose solution scheme can be applied in the actual job scheduling. As for the n-queen problem, backtracking algorithm is considered as an effective approach when the value of n is small. However, in case the value of n is large, the phenomenon of combination explosion is expected to occur. In order to solve the aforementioned problem, queen problems are firstly converted into the problem of function optimization with constraints, and then the corresponding mathematical model is established. Afterwards, the n-queen problem is solved by constructing the genetic operators and adaption functions using the integer coding based on the population search technology of the evolutionary computation. The experimental results demonstrate that the proposed algorithm is endowed with rapid calculation speed and high efficiency, and the model presents simple structure and is readily implemented.
Keywords:
Queen Problem, Function Optimization, Mathematical Model, Evolutionary Computation, Integer Coding

1. Introduction
As an old and well-known problem, the eight queens problem proposed by the international chess player, Marx Bethel, in 1848 is a typical case of the backtracking algorithm [1] . Since then, it has been studied by many mathematicians including Gauss and Cantos, and is generalized as the layout problem of the n-queen. The n-queen problem is an unstructured problem, which can be effectively solved using approaches including the search strategy based on artificial intelligence and the backtracking algorithm [2] - [5] . Some components, such as multi-leveled equations, graphics, and tables are not prescribed, although the various table text styles are provided. The formatter will need to create these components, incorporating the applicable criteria that follow.
As to the definition of the n-queen problem: n queens are placed on the international checkerboard with the dimension of the grid being n × n, and the precondition is that no queen suffers from the attack from another queen. That is to say, among the n queens, any two of them are not on the same row, column, or oblique line. There are many algorithms to solve this problem, such as the exhaustive method, backtracking algorithm, learning algorithm of the neural network, and so on. However, when the value of n is great, these algorithms take a long time for computation and therefore become infeasible.
Evolutionary computation is a global optimization based random search algorithm that simulates the natural selection and natural genetic mechanism of the biological evolution. Evolutionary computation has been applied in various fields including neural network, function optimization, image processing, system identification, expert system and so on due to its high efficiency and practicality through years of study. As for the application in solving the n-queen problems, evolutionary computation is an efficient nondeterministic algorithm [6] - [10] .
2. Modeling and Evolutionary Algorithm for n-Queen Problems
The general steps for solving a problem using the evolutionary computation are demonstrated as follows:
1) Analyzing the problem to determine a coding scheme;
2) Determining the objective function of the problem, to design a fitness function;
3) Generating an initial population that contains several individuals, each of which is a feasible solution of the problem;
4) Calculating the fitness values of each individual in the population;
5) If the optimal solution of the problem is found, quitting the cycle;
6) Performing the genetic operations including selection, hybridization and variation according to the fitness values of each individual;
7) Returning to step (4).
It is regulated in the n-queen problems that all queens are not in the same row, column, and oblique line. Assume that a layout of the n-queen problems is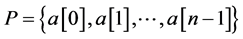 , where,
, where, 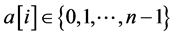 repre- sents that a queen is placed on the ith row and
repre- sents that a queen is placed on the ith row and 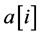 th column. Then, the n-adic queen problems are supposed to satisfy the following constraints:
th column. Then, the n-adic queen problems are supposed to satisfy the following constraints:
1) Any two queens are not in the same column, that is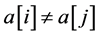 , (when
, (when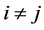 ).
).
2) Any two queens are not located in the same oblique line, namely, 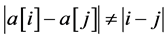 , (when
, (when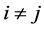 ).
).
A random function can be utilized to process the constraint 1, and the specific processing procedure is demonstrated as follows (Figure 1):
Constraint 2 can be converted into the objective function f:
Suppose that 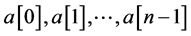 is an individual.
is an individual.
Let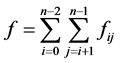 , where
, where 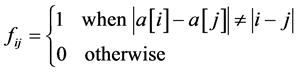
According to the definition of f, when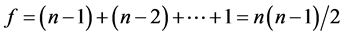 , we obtain
, we obtain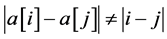 . Thereby, it is obtained that the individuals under such circumstance satisfy the requirements of the constraint 2.
. Thereby, it is obtained that the individuals under such circumstance satisfy the requirements of the constraint 2.
Figure 1. Condition 1 code.
Obviously, the greater the function value is, the smaller the possibility of the mutual attacks between queens. When the function value f reaches the maximum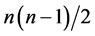 , the individual corresponding to the maximum value is the solution of the problem. Therefore, the function value f can be defined as the fitness function of the individuals.
, the individual corresponding to the maximum value is the solution of the problem. Therefore, the function value f can be defined as the fitness function of the individuals.
3. Algorithm
1) The aforementioned program segments are utilized to generate the initial population 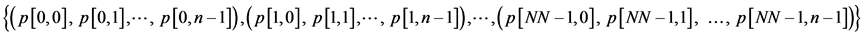 , where, NN and n represent the population size and the number of the queens respectively. The first and second subscripts in array p indicate the serial numbers of the individuals and genes separately, and are called the individual and gene respectively for the sake of convenience;
, where, NN and n represent the population size and the number of the queens respectively. The first and second subscripts in array p indicate the serial numbers of the individuals and genes separately, and are called the individual and gene respectively for the sake of convenience;
2) The fitness values 
3) Hybridization: the location based crossover operator is adopted, and the specific process is demonstrated as follows: to begin with, a random integer c with the value varying from 0 to n is randomly generated to be regarded as the crossover point. Afterwards, the optimal individual kmax is selected from the population, followed by the generation of a random integer m (m ≠ kmax and m ≠ kmin) with the value in the range of 0~NN. Then, the location based hybridization process is performed between the individual corresponding to the integer m and the optimal individual kmax at the point c. If the preferable individual in the hybrid progenies is superior to the optimal individual kmax, the worst individual kmin is replaced by the individual; otherwise, the worst individual kmin is reserved. The crossover operator is demonstrated in Figure 2, and its implementation algorithm is illustrated in Figure 3.
As demonstrated in Figure 3, the array element p[*,i] represents the value of the ith gene of the individual *, while ch1[i] and ch2[i] indicate the values of the ith gene in two generations respectively.
Figure 2. The crossover operator.
Figure 3. The crossover algorithm.
4) Variation: the locations of any two genes in the original optimal individual kmax in step 3 are exchanged, to generate a new individual. If the new individual is superior to the previous optimal individual kmax, the latter is replaced by the former; otherwise, the latter is reserved.
5) Recalculating the values of fitness, maximum and minimum of the individuals changed by the hybridization and variation processes;
6) The results are output if the termination condition is satisfied, that is, output all the individuals i that satisfy the condition; otherwise, step 3 is repeated.
4. Operation Results
By using the proposed algorithm nearly all the solutions of the 4 queens problem (n = 4) are obtained in the test. Limited by the length of the paper, merely parts of the operation results are demonstrated, as illustrated in Table 1.
The value of the population size in the algorithm is generally taken as 10 - 20 times of the number of the queens. The evolution generation can be adjusted in the range of 50 - 100 times of the number of the queens, and the termination condition of the evolution is
5. Conclusion and Improvement
The construction of the fitness functions using integers shortens the evaluation time of the computers, and thus greatly improves the calculation efficiency. Meanwhile, integer coding is performed on the individuals, which applies the knowledge of the n-queen problems and makes the algorithm concise and visual. The experimental results demonstrate that this algorithm is endowed with rapid calculation and high efficiency. Of course, in order to further improve the operating speed, several crossover points can be added according to the variation of the
Table 1. Experimental results.
fitness functions while designing the evolutionary operators. That is to say, the smaller the fitness value of the optimal individual is, the more the crossover points. With the gradual increase of the fitness value of the optimal individuals in the evolution process, the number of the crossover points is gradually reduced. When the difference between the fitness value and the integer n(n − 1)/2 is smaller than certain a given positive number, the number of the crossover points is changed to 1. In this way, the evolution speed of the population is accelerated, which gives rise to the improved efficiency of the algorithm. In addition, in order to avoid the local optimum of the programs, the stability of the system requires to be further improved.
Cite this paper
Nengfa Hu, (2016) An Integer Coding Based Optimization Model for Queen Problems. American Journal of Computational Mathematics,06,32-36. doi: 10.4236/ajcm.2016.61004
References
- 1. Dahl, O.J., Dijkstra, E.W. and Hoare, C.A.R. (1972) Structured Programming. Academic Press, London.
- 2. Kryszkiewicz, M. (1998) Rough Set Approach to Incomplete Information Systems. Information Sciences, 112, 39-49.
http://dx.doi.org/10.1016/S0020-0255(98)10019-1 - 3. Kryszkiewicz, M. (1999) Rules in Incomplete Information Systems. Information Sciences, 113, 271-292.
http://dx.doi.org/10.1016/S0020-0255(98)10065-8 - 4. Stefanowski, J. and Tsoukias, A. (1999) On the Extension of Rough Sets under Incomplete Information. Proceedings of 7th International Workshop on New Directions in Rough Sets, Data Mining, and Granular Soft Computing, Physica-Verlag, Yamaguchi, 73-81.
http://dx.doi.org/10.1007/978-3-540-48061-7_11 - 5. Slowinski, R. and Vanderpooten, D. (2000) A Generalized Definition of Rough Approximation Based on Similarity. IEEE Transactions on Knowledge and Data Engineering, 12, 331-336.
http://dx.doi.org/10.1109/69.842271 - 6. Holland, J.H. (1992) Adaptation in Natural and Artificial Systems. MIT Press, Cambridge.
- 7. Darwin, C. and Burrow, J.W. (2009) The Origin of Species by Means of Natural Selection: The Preservation of Favoured Races in the Struggle for Life. Penguin Classics, USA, 2-3.
http://dx.doi.org/10.1017/CBO9780511694295 - 8. Darwin, C. (1994) The Descent of Man, and Selection in Relation to Sex. John Murray, London.
- 9. Moore, A.J. (1990) The Evolution of Sexual Dimorphism by Sexual Selection: The Separate Effects of Intrasexual Selection and Intersexual Selection. Evolution, 34, 315-331.
http://dx.doi.org/10.2307/2409410 - 10. Fisher, R.A. (1995) The Evolution of Sexual Preference. Eugenics Review, 7, 184-192.





