American Journal of Computational Mathematics
Vol.05 No.03(2015), Article ID:59296,8 pages
10.4236/ajcm.2015.53023
A New Symbolic Algorithm for Solving General Opposite-Bordered Tridiagonal Linear Systems
Faiz Atlan*, Moawwad El-Mikkawy
Mathematics Department, Faculty of Science, Mansoura University, Mansoura, Egypt
Email: *faizatlan11@yahoo.com, m_elmikkawy@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 June 2015; accepted 28 August 2015; published 31 August 2015
ABSTRACT
In the current article we propose a new efficient, reliable and breakdown-free algorithm for solving general opposite-bordered tridiagonal linear systems. An explicit formula for computing the determinant of an opposite-bordered tridiagonal matrix is investigated. Some illustrative examples are given.
Keywords:
Opposite-Bordered Tridiagonal Matrix, Algorithm, Linear System of Equations, Schur Complement, MATLAB

1. Introduction
The 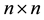 general tridiagonal matrix
general tridiagonal matrix  takes the form:
takes the form:
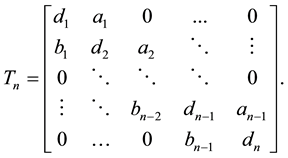 (1)
(1)
The matrix in (1) frequently appears in many applications, for example, in parallel computing, telecommu- nication system analysis, solving differential equations using finite differences, heat conduction and fluid flow problems. The interested reader may refer to [1] - [12] and the references therein.
Inverting tridiagonal matrices in (1) have been considered by many authors. See for instance, [13] - [22] . To study matrices of the form (1) it is advantageous to introduce an n-dimensional vector 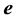 in the following way [23] :
in the following way [23] :
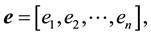 (2)
(2)
whose components 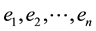 are given by:
are given by:
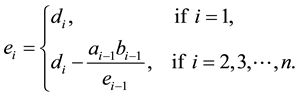 (3)
(3)
The symbolic algorithm DETGTRI [23] is based on (2) and (3). By using the LU factorization of , it is known that [23]
, it is known that [23]
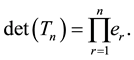 (4)
(4)
There are great interests in solving general opposite-bordered tridiagonal linear system, and hereafter it will be referred to as OBTLS, of the form:
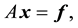 (5)
(5)
in which the coefficient matrix A is given by:
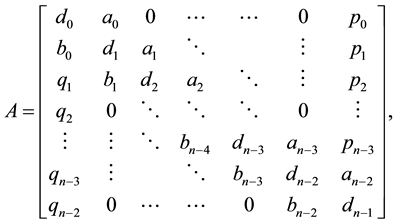 (6)
(6)
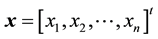 and
and
This system frequently occurs in engineering computation and science, e.g. in the numerical solution of an ablation and heat transfer problem as referred in [24] - [28] . The matrix A in (6) can be stored in 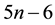 memory locations only.
memory locations only.
In [28] , the author presented a numeric algorithm for solving the linear system (5) with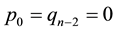 . The algorithm is based on the elementary column operations (ECO’s). It is noted that the numerical algorithm in [28] fails to solve some OBTLS of the form (5). Therefore, the main objective of the present paper is to construct a new symbolic and breakdown-free algorithm for solving the OBTLS in (5).
. The algorithm is based on the elementary column operations (ECO’s). It is noted that the numerical algorithm in [28] fails to solve some OBTLS of the form (5). Therefore, the main objective of the present paper is to construct a new symbolic and breakdown-free algorithm for solving the OBTLS in (5).
Throughout this paper, the word “simplify” means simplifying the algebraic expression under consideration to its simplest rational form. Also, 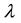 is a formal parameter which can be treated as a symbolic name whose actual value is 0 as we will see later.
is a formal parameter which can be treated as a symbolic name whose actual value is 0 as we will see later.
The organization of the paper is as follows. The main results are given in the next section. Some illustrative examples are given in Section 3. In Section 4, we present some concluding remarks.
2. Main Results
In this section, we are going to formulate a new algorithm for solving OBTLS of the form (5). We begin by considering the singly bordered tridiagonal linear systems of the form (7)-(8) below.
2.1. A Symbolic Algorithm for Solving Singly Bordered Tridiagonal Linear Systems
The 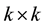 singly bordered tridiagonal linear system takes the form:
singly bordered tridiagonal linear system takes the form:

where


The Doolittle LU factorization of 

where

and

where the quantities 




and

It follows from (9)-(11) that

At this point, it should be mentioned that the above 

The solution of the system in (7) reduces to solving the two standard linear systems:

and

We are now ready to formulate the following algorithm for solving the linear system (7).
2.2. A Symbolic Algorithm for Solving General OBTLS
In order to solve the general OBTLS (5) it is convenient to introduce the following notations:



and
Based on the above notations, the linear system in (5) can be written in the partitioned form:

The solution of the linear system (21), may be obtained by solving the two linear systems:


It is not difficult to prove that:

As can be seen from (24), we need to compute 




Consequently, we have from (24)

and

By substituting (26) and (27) into (22), it follows that

Therefore, we get

Hence, the solution vector of the OBTLS (5) is
The proofs of the following result may be found in [29] .
Theorem 1. (Schur determinant identity) Let 








Then
By noticing (21), we see that the matrix 

Hence, by applying Theorem 1 on this matrix, we get the following result:
Corollary 1. Let 



provided 
The main result of the present paper may now be formulated as follows:
This algorithm will be referred to as the OBS algorithm. The computational cost for OBS is 
A MATLAB code based on the OBS algorithm is available upon request from the authors.
3. Illustrative Examples
In this section we are going to consider some illustrative examples. The, symbolic computations are performed in Example 1 by using MATLAB with Symbolic Math Toolbox. Also, we compare the proposed algorithm with MATLAB back-slash and the algorithm in [28] by means of execution times and accuracy of the solutions in Example 2. Finally, we give Example 3 in order to demonstrate the validity of the OBS algorithm. All experiments were carried out using MATLAB 7.10.0.499 (R2010a) on a PC with Intel(R) Core(TM) i7-3770 CPU processor.
Example 1. Solve the opposite-bordered tridiagonal linear system:

Solution.
Here, 
The numeric algorithm in [28] fails to solve the linear system (33) although 



The solution vector 
Example 2. Consider the opposite-bordered tridiagonal linear system:

The exact solution of this system is 
tained from the OBS algorithm, the algorithm in [28] and MATLAB back-slash operator for n = 1000, 2000, 


Example 3. Consider the opposite-bordered tridiagonal linear system:

Table 2 gives the absolute errors and CPU times (after 100 tests) obtained from the OBS algorithm for n = 1000, 5000, 10,000, 20,000, 30,000, 40,000, 50,000.
Table 1. Mean value of the CPU times after 100 tests.
Figure 1. Absolute errors for Example 2.
Table 2. Absolute errors and CPU times of Example 3 for the OBS algorithm.
4. Conclusion
In this paper, we proposed a new efficient and reliable algorithm for solving general opposite-bordered tridia- gonal linear systems in linear time. An explicit formula for computing the determinant of an opposite-bordered tridiagonal matrix is obtained. Some illustrative examples are given.
Acknowledgements
The authors wish to thank anonymous referees and the editorial board of the AJCM for careful reading of the manuscript and their useful comments.
Cite this paper
FaizAtlan,MoawwadEl-Mikkawy, (2015) A New Symbolic Algorithm for Solving General Opposite-Bordered Tridiagonal Linear Systems. American Journal of Computational Mathematics,05,258-266. doi: 10.4236/ajcm.2015.53023
References
- 1. Burden, R.L. and Faires, J.D. (2001) Numerical Analysis. 7th Edition, Books & Cole Publishing, Pacific Grove.
- 2. da Fonseca, C.M. and Petronilho, J. (2001) Explicit Inverses of Some Tridiagonal Matrices. Linear Algebra and its Applications, 325, 7-21.
http://dx.doi.org/10.1016/S0024-3795(00)00289-5 - 3. El-Mikkawy, M.E.A. (2005) A New Computational Algorithm for Solving Periodic Tri-Diagonal Linear Systems. Applied Mathematics and Computation, 161, 691-696.
http://dx.doi.org/10.1016/S0024-3795(00)00289-5 - 4. El-Mikkawy, M.E.A. and Karawia, A. (2006) Inversion of General Tridiagonal Matrices. Applied Mathematics Letters, 19, 712-720.
http://dx.doi.org/10.1016/j.aml.2005.11.012 - 5. El-Mikkawy, M. and Atlan, F. (2014) Algorithms for Solving Linear Systems of Equations of Tridiagonal Type via Transformations. Applied Mathematics, 5, 413-422.
http://dx.doi.org/10.4236/am.2014.53042 - 6. El-Mikkawy, M. and Atlan, F. (2014) Algorithms for Solving Doubly Bordered Tridiagonal Linear Systems. British Journal of Mathematics & Computer Science, 4, 1246-1267.
http://dx.doi.org/10.9734/BJMCS/2014/8835 - 7. El-Mikkawy, M., El-Shehawy, M. and Shehab, N. (2015) Solving Doubly Bordered Tridiagonal Linear Systems via Partition. Applied Mathematics, 6, 967-978.
http://dx.doi.org/10.4236/am.2015.66089 - 8. Golub, G.H. and van Loan, C.F. (1996) Matrix Computations. 3rd Edition, Johns Hopkins University Press, Baltimore.
- 9. Kavcic, A. and Moura, J.M.F. (2000) Matrices with Banded Inverses: Inversion Algorithms and Factorization of Gauss-Markov Processes. IEEE Transactions on Information Theory, 46, 1495-1509.
http://dx.doi.org/10.1109/18.954748 - 10. Li, H.-B., Huang, T.-Z., Liu, X.-P. and Li, H. (2010) On the Inverses of General Tridiagonal Matrices. Linear Algebra and Its Applications, 433, 965-983.
http://dx.doi.org/10.1016/j.laa.2010.04.042 - 11. Mazilu, I., Mazilu, D.A. and Williams, H.T. (2012) Applications of Tridiagonal Matrices in Non-Equilibrium Statistical Physics. Electronic Journal of Linear Algebra, 24, 7-17.
- 12. Olcayto, E. (1979) Recursive Formulae for Ladder Network Optimization. Electronics Letters, 15, 249-250.
http://dx.doi.org/10.1049/el:19790176 - 13. El-Mikkawy, M.E.A. (2004) On the Inverse of a General Tridiagonal Matrix. Applied Mathematics and Computation, 150, 669-679.
http://dx.doi.org/10.1016/S0096-3003(03)00298-4 - 14. El-Mikkawy, M.E.A. and El-Desouky, R. (2008) A New Recursive Algorithm for Inverting General Tridiagonal and Anti-Tridiagonal Matrices. Applied Mathematics and Computation, 204, 368-372.
http://dx.doi.org/10.1016/j.amc.2008.06.053 - 15. Huang, Y. and McColl, W.F. (1997) Analytic Inversion of General Tridiagonal Matrices. Journal of Physics A, 30, 7919-7933.
http://dx.doi.org/10.1088/0305-4470/30/22/026 - 16. Hu, G.Y. and O’Connell, R.F. (1996) Analytical Inversion of Symmetric Tridiagonal Matrices. Journal of Physics A, 29, 1511-1513.
http://dx.doi.org/10.1088/0305-4470/29/7/020 - 17. Mallik, R.K. (2001) The Inverse of a Tridiagonal Matrix. Linear Algebra and Its Applications, 325, 109-139.
http://dx.doi.org/10.1016/S0024-3795(00)00262-7 - 18. Marrero, J.A., Rachidi, M. and Tomeo, V. (2013) Non-Symbolic Algorithms for the Inversion of Tridiagonal Matrices. Journal of Computational and Applied Mathematics, 252, 3-11.
http://dx.doi.org/10.1016/j.cam.2012.05.003 - 19. Ran, R.-S., Huang, T.-Z., Liu, X.-P. and Gu, T.-X. (2009) An Inversion Algorithm for General Tridiagonal Matrix. Applied Mathematics and Mechanics, 30, 247-253.
http://dx.doi.org/10.1007/s10483-009-0212-x - 20. Sugimoto, T. (2012) On an Inverse Formula of a Tridiagonal Matrix. Operators and Matrices, 6, 465-480.
http://dx.doi.org/10.7153/oam-06-30 - 21. Usmani, R. (1994) Inversion of a Tridiagonal Jacobi Matrix. Linear Algebra and Its Applications, 212/213, 413-414.
http://dx.doi.org/10.1016/0024-3795(94)90414-6 - 22. Yamamoto, T. and Ikebe, Y. (1979) Inversion of Band Matrices. Linear Algebra and Its Applications, 24, 105-111.
http://dx.doi.org/10.1016/0024-3795(79)90151-4 - 23. El-Mikkawy, M.E.A. (2004) A Fast Algorithm for Evaluating nth Order Tri-Diagonal Determinants. Journal of Computational and Applied Mathematics, 166, 581-584.
http://dx.doi.org/10.1016/j.cam.2003.08.044 - 24. Amar, A.J., Blackwell, B.F. and Edward, J.R. (2006) One-Dimensional Ablation Using a Full Newton’s Method and Finite Control Volume Procedure. 9th AIAA/ASME Joint Thermophysics and Heat Transfer Conference, AIAA-2006-2910, San Francisco, 5-8 June 2006, 26.
http://dx.doi.org/10.2514/6.2006-2910 - 25. Amar, A.J., Blackwell, B.F. and Edward, J.R. (2007) One-Dimensional Ablation with Pyrolysis Gas Flow Using a Full Newton’s Method and Finite Control Volume Procedure. 39th AIAA Thermophysics Conference, AIAA-2007-4535, Miami, 25-28 June 2007, 41.
http://dx.doi.org/10.2514/6.2007-4535 - 26. Martin, A., Reggio, M., Trepanier, J.Y. and Guo, X. (2007) Transient Ablation Regime in Circuit Breakers. Plasma Science and Technology, 9, 653-656.
http://dx.doi.org/10.1088/1009-0630/9/6/02 - 27. Martin, A. and Boyd, I.D. (2008) Simulation of Pyrolysis Gas within a Thermal Protection System. 40th AIAA Thermophysics Conference, AIAA-2008-3805, Seattle, 23-26 June 2008.
http://dx.doi.org/10.2514/6.2008-3805 - 28. Martin, A. and Boyd, I.D. (2010) Variant of the Thomas Algorithm for Opposite-Bordered Tridiagonal Systems of Equations. International Journal for Numerical Methods in Biomedical Engineering, 26, 752-759.
- 29. Meyer, C.D. (2000) Matrix Analysis and Applied Linear Algebra. SIAM, Philadelphia.
http://dx.doi.org/10.1137/1.9780898719512.
NOTES
*Corresponding author.

















