American Journal of Computational Mathematics
Vol.04 No.04(2014), Article ID:49500,6 pages
10.4236/ajcm.2014.44026
The Peculiarity of Numerical Solving the Euler and Navier-Stokes Equations
Ludmila Petrova
Department of Computational Mathematics and Cybernetics, Moscow State University, Moscow, Russia
Email: ptr@cs.msu.su
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 June 2014; revised 23 July 2014; accepted 6 August 2014
ABSTRACT
The analysis of integrability of the Euler and Navier-Stokes equations shows that these equations have the solutions of two types: 1) solutions that are defined on the tangent nonintegrable manifold and 2) solutions that are defined on integrable structures (that are realized discretely under the conditions related to some degrees of freedom). Since such solutions are defined on different spatial objects, they cannot be obtained by a continuous numerical simulation of derivatives. To obtain a complete solution of the Euler and Navier-Stokes equations by numerical simulation, it is necessary to use two different frames of reference.
Keywords:
Solutions of Two Types, Nonintegrable Manifolds and Integrable Structures, Discrete Transitions, Two Different Frames of Reference

1. Introduction
As it is known, the Euler and Navier-Stokes equations are made up of the conservation law equations for energy, momentum and mass.
Under an investigation of the consistency of the conservation law equations involved into the set of Euler and Navier-Stokes equations obtains the nonidentical evolutionary relation for entropy as a functional which specifies the state of flow as a material medium. Such a relation discloses the peculiarities of the solutions to the Euler and Navier-Stokes equations and possibilities of finding these solutions by the numerical methods.
From the evolutionary relation it follows that the Navier-Stokes equations possess solutions of two types, namely, the solution on nonintegrable manifold (like a tangent one) and the solution on integrable structures.
The solutions of the first type are not functions, because the derivatives of such a solution do not made up the differential. These solutions describe a nonequilibrium state of a flow (of a fluid or gas).
The solutions on integrable structures (on which the derivatives made up the interior differential: it asserts only on structure) are discrete functions.
The transition from the solutions of the first type to that of the second type describes a transition from nonequilibrium state of a flow to locally-equilibrium state. This process is accompanied by the origination of a vorticity or turbulence.
To obtain a complete solution of the Euler and Navier-Stokes equations by numerical simulation, it is necessary to use two different frames of reference.
2. Analysis of the Consistency of Equations in the Set of Euler and Navier-Stokes Equations. Evolutionary Relation
Integrability and the properties of solutions to the set of differential equations depend on whether or not the equations in the set of differential equations are consistent. (It should be noted that the functional properties of solutions to differential equations in addition depend on whether or not the derivatives of differential equations are conjugacy.)
Let us consider the gas-dynamic systems for ideal (inviscid) and viscous gases that are respectively described by Euler or Navier-Stokes equations, which include the conservation laws for energy, linear momentum and mass.
The problem of consistency of equations can be studied only with the help of two nonequivalent frames of reference.
Let us introduce two frames of reference: an inertial one, which is not connected with the gas-dynamic system, and an accompanying frame of reference being connected with the manifold made up by the trajectories of the system elements. (Both Euler’s and Lagrange’s coordinate systems can be treated as examples of such systems.)
Let us analyze the consistency of the equations that describe the conservation laws for energy and linear momentum.
In the inertial frame of reference the equation of conservation law for energy can be written a
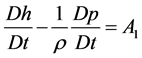 (1)
(1)
where 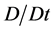 is the total derivative with respect to time, p,
is the total derivative with respect to time, p,  and h are respectively the pressure, density and enthalpy of a gas.
and h are respectively the pressure, density and enthalpy of a gas.
In the case of ideal gas described by the Euler equations we have
 (2)
(2)
And in the case of viscous heat-conducting gas described by the Navier-Stokes equations expression  can be written as (see [1] , Chapter 6, formulas (6.2.4))
can be written as (see [1] , Chapter 6, formulas (6.2.4))
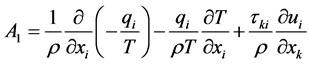 (3)
(3)
Here 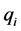 is the heat flux and
is the heat flux and 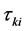 is the viscous stress tensor.
is the viscous stress tensor.
Expressing enthalpy in terms of internal energy e with the help of formula 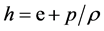 and using relation
and using relation 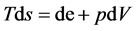 Equation (1) of the conservation law for energy can be reduced to the form
Equation (1) of the conservation law for energy can be reduced to the form
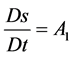 (4)
(4)
Here s is the entropy.
Since the total derivative with respect to time is that along the trajectory, in the accompanying frame of reference the equation of the conservation law for energy takes the for
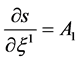 (5)
(5)
where 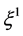 is the coordinate along the trajectory.
is the coordinate along the trajectory.
In the accompanying frame of reference the equation of conservation law for linear momentum can be presented as
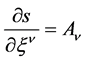 (6)
(6)
where  is the coordinate in the direction normal to the trajectory.
is the coordinate in the direction normal to the trajectory.
In the case of two-dimensional ideal gas, from the Euler equation one can obtain the following expression for coefficient 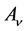 (see [1] , Chapter 6, formulas (6.7.12)):
(see [1] , Chapter 6, formulas (6.7.12)):

where
In the case of viscous gas the expression 
Equations (5) and (6) can be convoluted into the relation

where 

Since the equations of conservation laws are evolutionary ones, the relation obtained is also an evolutionary relation. In this case the skew-symmetric form 
3. Nonidentity of the Evolutionary Relation. Inexact Solutions to the Euler and Navier-Stokes Equations
Evolutionary relation (8) is a nonidentical one as it involves the skew-symmetric differential form


The differential of evolutionary form 

where 

The coefficients 





Nonidentity of the evolutionary relation means that the equations of conservation laws for energy and linear momentum (entered into the set of Euler and Navier-Stokes equations) appear to be inconsistent. They cannot be convolved into identical relation for obtaining a differential. This points out to the fact that the Euler and Navier- Stokes equations turn out to be nonintegrable.
This means that the solutions to the Euler and Navier-Stokes equations cannot be functions (depending only on coordinates). Such solutions will depend on the commutator of form
4. Degenerate Transformations. Exact Solutions to the Euler and Navier-Stokes Equations
From the properties of nonidentical evolutionary relation it follows that the Euler and Navier-Stokes equations can have exact solutions.
This is possible only in the case when from the evolutionary skew-symmetric form 
From the evolutionary unclosed form
Degenerate transformations can take place under additional conditions, which relate to degrees of freedom. (To this case a vanishing of such functional expressions as determinants, Jacobians, Poisson's brackets, residues and others can be assigned.)
The conditions of degenerate transformation specify the integrable structures (pseudostructures): the characteristics (the determinant of coefficients at the normal derivatives vanishes), the singular points (Jacobian is equal to zero), the envelopes of characteristics of the Euler equations and so on.
The conditions of degenerate transformation can be realized under change of nonidentical evolutionary relation, which appears to be a selfvarying relation.
On integral structure (the pseudostructure


Here the subscript 


There are differentials in the left-hand and right-hand side of relation (10). This means that the relation obtained is an identical one.
Identity of the relation means that the equations of conservation laws for energy and linear momentum (entered into the set of Euler and Navier-Stokes equations) appear to be consistent. This points out to the fact that the Euler and Navier-Stokes equations turn out to be integrable since they can be convolved into relation made up of the differentials.
On the integrable structure the solution to Euler and Navier-Stokes equations becomes exact one, i.e. it is a function (depending only on coordinates). This is so-called generalized solution. This solution is discrete function since it is realized only under additional conditions. As the relevant functions are defined only on integrable structures or surfaces (made up by integrable structures), these functions or their derivatives suffer a discontinuity along the directions being normal to integral structures or surfaces [2] . It is evident that such discontinuities are described by the evolutionary form commutator.
Here it must be emphasized that inexact solutions to the Euler and Navier-Stokes equations are solutions with derivatives defined on tangent (nonintegrable) manifold whereas the derivatives of generalized functions are defined on integrable structures that can be only on cotangent (integrable) manifold.
One can see that the transition from inexact solution to exact solution is a transition from tangent to cotangent manifold. (Here it is worth noting, that coordinates on integrable structures are not identical to the independent coordinates of the initial manifold on which equations defined.)
Mathematically to this it is assigned a transition under the degenerate transformation from one frame of reference to another nonequivalent frame of reference (from accompanying frame of reference to a locally-inertial on integral structures obtained).
At numerical solving the Euler and Navier-Stokes equations one cannot obtain such a degenerate transformation only by direct modeling the derivatives of these equations.
Here it should be emphasized that at numerical solving the Euler and Navier-Stokes equations one cannot obtain a generalized (exact) solution by modeling derivatives of these equations on original tangent manifold.
Thus, it has been shown that the Euler and Navier-Stokes equations have solutions of two types.
The Euler and Navier-Stokes equations are used for description of physical quantities (such as energy, pressure and density) that specify a flow of a fluid or gas. But, it appears that obtained solutions to the Euler and Navier-Stokes enable to describe evolutionary processes proceeding in a gas-dynamic system as a material medium (in a general case, in fluxes of fluid and gas) and to explain the processes of origination of vorticity and turbulence. The realization of these possibilities are related to double solutions of the Euler and Navier-Stokes equations.
5. Physical Meaning of Solutions to the Euler and Navier-Stokes Equations. The Evolutionary Processes in Gas-Dynamic Systems
The further analysis of the evolutionary relation allows disclosing a physical meaning of obtained solutions, their role in evolutionary processes proceeding in gas-dynamic systems.
The evolutionary relation in addition to mathematical properties possesses unique physical properties. This is due to the fact that this relation includes the entropy, which specifies the state of gas-dynamic system.
5.1. Physical Meaning of Inexact Solutions to the Euler and Navier-Stokes Equations. Non-Equilibrium of a Gas-Dynamic System
The solutions that are not functions (inexact solutions) have a physical meaning. Namely, they describe a non-equilibrium state of gas-dynamic system. This follows from the evolutionary relation.
If from relation (8) the differential of entropy could be obtained, this would point to the fact that entropy is a state function. And this would mean that the state of a gas-dynamic system is an equilibrium one.
But, since relation (8) is a nonidentical relation, from that one cannot obtain the differential of entropy and find the state function. This means that the gas-dynamic system is in a non-equilibrium state. On the other hand, as this has been shown, the nonidentity of evolutionary relation points out to the fact that in this case the solutions to Euler and Navier-Stokes equations are solutions of first type, i.e., they are inexact solutions (which are not functions). As a result, the solutions of first type to the Euler and Navier-Stokes equations, which are inexact, are assigned to non-equilibrium state of gas-dynamic system.
The nonequilibrium means that in gas-dynamic system an internal force acts. It is evident that the internal force is described by the commutator of skew-symmetric form

(Here it may be noted that the nonidentity of a relation is connected with a noncommutativity of the conservation laws. This points out to the fact that the noncommutativity of the conservation laws is a cause of a non- equilibrium state of gas-dynamic system.)
Evolutionary relation also describes a variation of non-equilibrium state. This is due to another peculiarity of nonidentical evolutionary relation, namely, as it was already noted, this relation is a selfvarying one.
Selfvarying of evolutionary relation points out to the fact that the gas-dynamic system state changes. However, since the nonidentity of evolutionary relation holds, the gas-dynamic system state remains nonequilibrium. (Such a change of non-equilibrium state of gas-dynamic system can lead to increasing nonequilibrium and developing instability.) The process of selfvariation of evolutionary relation proceeds under the action of internal force and is described by inexact solutions. In this case, as it was already noted, the evolutionary form commutator, on which the inexact solution depends, describes an internal force.
5.2. Physical Meaning of Exact Solutions to the Euler and Navier-Stokes Equations. Transition of Gas-Dynamic System into a Locally-Equilibrium State
As it has been shown above, under degenerate transformation the identical relation is obtained from nonidentical one. From identical relation one can obtain the differential of entropy ds and find entropy s as a function of space-time coordinates. It is precisely the entropy that will be a gas-dynamic function of state. The availability of gas-dynamic function of state would point out to equilibrium state of gas-dynamic system. However, since the identical relation is satisfied only under additional conditions, such a state of gas-dynamic system will be a locally-equilibrium one. The identity of relation points out to the fact that in this case the solutions to Euler and Navier-Stokes equations are exact solutions (which are functions). As a result, the exact solutions equations to the Euler and Navier-Stokes are assigned to locally-equilibrium state of gas-dynamic system. [Notice that the entropy in the evolutionary relation for gas-dynamic system depends on space-time coordinates since the differential of entropy ds in evolutionary relation has been made up by derivatives of entropy with respect to space- time coordinates. (The entropy, which depends on thermodynamic variables, is a state function only of thermodynamic system. In the gas-dynamic system the entropy depended on thermodynamical variables characterizes only the state of a gas rather than the state of gas-dynamic system itself.)]
It is evident that the transition from inexact solutions to exact (generalized) solutions describes a transition of gas-dynamic system from a non-equilibrium state to a locally-equilibrium state.
Such the transition describes process of emergence of observable formations (as waves, vortices, turbulent pulsations).
5.3. Mechanism of Arising Observable Formations and Origination of Vorticity and Turbulence
Since the non-equilibrium state has been induced by an availability of internal force and in the case of locally- equilibrium state there is no internal force (in local domain of gas-dynamic system), it is evident that under transition of gas-dynamic system from non-equilibrium state into locally-equilibrium state the nonmeasurable quantity, which acted as internal force, changes to a measurable quantity. This manifests itself in the form of arising a certain observable measurable formation. Waves, vortices, turbulent pulsations and so on are examples of such formations.
Exact generalized solutions to the Euler and Navier-Stokes equations describe such observable quantities arisen. It is evident that the transition from inexact solutions to exact (generalized) solutions describes a transition of gas-dynamic system from a non-equilibrium state to a locally-equilibrium state and the process of emergence of observable formations. In this case the discontinuities of function, which correspond to generalized solutions, or their derivatives are defined by a quantity that is described by the commutator of unclosed form 
The process of arising observable formations discloses a mechanism of such phenomena as an emergence of vorticity and turbulence.
Thus, the analysis of evolutionary relation obtained from the Euler and Navier-Stokes equations showed that these equations have solutions of two types, namely, inexact solutions being assigned to non-equilibrium state of gas-dynamic system and exact generalized solutions, which corresponds to the locally-equilibrium state of gas-dynamic system. In this case the transition from inexact solution to exact one points out to the transition of gas-dynamic system from non-equilibrium state to locally-equilibrium state and this process is accompanied by emergence of observable formations, which are described by generalized solutions.
Such properties of solutions to the Euler and Navier-Stokes equations enable one to disclose the mechanism of development of instability and arising vorticity and turbulence.
6. On the Problem of Numerical Solving the Euler and Navier-Stokes Equations
It has been shown that the origin of discrete formations (such as waves, vortices, turbulent pulsations, and others) is described by the transition from the solutions of the first type which are not functions to the generalized solutions that are functions.
To describe evolutionary processes proceeding in a gas-dynamic system and the process of origin of discrete formations, it is necessary have the solutions of the first type and the solution of the second type (generalized solution).
Problems of numerical solving the Euler and Navier-Stokes equations relates to the fact that these solutions are defined on distinct spatial objects.
The solutions of one type are defined on the tangent nonintegrable manifold, whereas the solutions of another type are defined on integrable structures. Since the solutions are defined on distinct spatial objects, they cannot be obtained by a continuous numerical simulation of derivatives. So, it turns out to be impossible to describe the origination of vorticity and turbulence by this way.
The solutions of first type can be obtained only by numerical modeling the equations on the original nonintegrable manifold (it is impossible to find such a solution by analytical method). The solutions of the second type (generalized solution), cannot be obtained by modeling the equations on original manifold, since they are obtained on integrable structures that do not belong to original nonintegrable manifold.
To obtain the generalized solutions by numerical simulation, one must use second systems of reference (on integrable structure). Therefore, to describe the origination of vorticity and turbulence by numerical simulation, one must use two systems of reference.
One more problem of obtaining the generalized solution relates to the fact that the integrable structures with generalized solution are not initially given, and they are realized spontaneously in the process of integrating under the realization of additional conditions, namely, the integrability conditions. (As additional conditions it may serve, for example, the characteristic conditions, the dynamical conditions of the consistency of equations in the set of equations [3] and so on.) To obtain the integrable structures, it is necessary to trace for the realization of additional conditions, which define the integrable structures, in the process of numerical integrating the equations on the original manifold.
Here there is another possibility.
The generalized solutions can be obtained by analytical methods if the integrability conditions are imposed on the equations. The methods of characteristics, symmetries, eigen-functions and others are examples of such methods. However, in this case it is impossible to describe the process of the discrete formation emergence.
The description of evolutionary processes is possible only either by numerical methods, but with two frames of reference, or by using simultaneously numerical and analytical methods.
In mechanics and physics the interest is expressed in various types of solutions to equations. The methods of solving the Euler and Navier-Stokes the equations relate to this fact.
In mechanics this is the method of direct numerical simulating the equations, which is fulfilled on tangent manifold (being nonintegrable) and enables one to obtain only inexact solutions. It turns out to be impossible to describe of discrete formations by this way.
In physics this is the method of solving equations when the equations are provided with the integrability conditions (the conditions of consistency) and this enables one to obtain exact solutions. The analytical methods may be such methods. However, such method does not give a possibility to describe evolutionary processes.
It is possible that the integration of these both methods will allow solving some problems on numerical integrating of the Euler and Navier-Stokes equations.
7. Conclusions
It has been shown that the Euler and Navier-Stokes equations have the solutions of two types, which are defined on distinct spatial objects, and, therefore, cannot be obtained by continuous numerical simulation of the equations. The existence of two spatial objects on which the solutions are defined gives rise to the problems on which the attention must be focused at numerical solving the Euler and Navier-Stokes equations.
It should be also emphasized that the methods of numerical solving the equations taking into account for the existence of two types of solutions can allow describing the evolutionary processes such as the emergence of any discrete formations.
These results are obtained with use of the skew-symmetric forms that are defined on nonintegrable manifolds [4] .
References
- Clarke, J.F. and Machesney, M. (1964) The Dynamics of Real Gases. Butterworths, London.
- Petrova, L.I. (2009) Relationships between Discontinuities of Derivatives on Characteristics and Trajectories. Computational Mathematics and Modeling, 20, 367-372. http://dx.doi.org/10.1007/s10598-009-9043-0
- Smirnov, V.I. (1957) A Course of Higher Mathematics. Moscow, Tech. Theor. Lit., 4.
- Petrova, L.I. (2010) Role of Skew-Symmetric Differential Forms in Mathematics. http://arxiv.org/abs/1007.4757


