Received 22 February 2015; accepted 22 May 2015; published 25 May 2015

ABSTRACT

In this article, we study necessary and sufficient conditions for a function, defined on the space of flags to be the projection curvature radius function for a convex body. This type of inverse problems has been studied by Christoffel, Minkwoski for the case of mean and Gauss curvatures. We suggest an algorithm of reconstruction of a convex body from its projection curvature radius function by finding a representation for the support function of the body. We lead the problem to a system of differential equations of second order on the sphere and solve it applying a consistency method suggested by the author of the article.

Keywords:

Integral Geometry, Convex Body, Projection Curvature, Support Function

1. Introduction

The problem of reconstruction of a convex body from the mean and Gauss curvatures of the boundary of the body goes back to Christoffel and Minkwoski [1] . Let F be a function defined on 2-dimensional unit sphere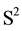. The following problems have been studied by E. B. Christoffel: what are necessary and sufficient conditions for F to be the mean curvature radius function for a convex body. The corresponding problem for Gauss curvature is considered by H. Minkovski [1] . W. Blaschke [2] provides a formula for reconstruction of a convex body B from the mean curvatures of its boundary. The formula is written in terms of spherical harmonics.

A. D. Aleksandrov and A. V. Pogorelov generalize these problems for a class of symmetric functions 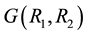of principal radii of curvatures (see [3] -[5] ).

Let 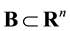be a convex body with sufficiently smooth boundary and let signify the principal radii of curvature of the boundary of B at the point with outer normal direction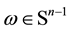. In n-dimen- sional case, a Christoffel-Minkovski problem is posed and solved by Firay [6] and Berg [7] (see also [8] ): what are necessary and sufficient conditions for a function F, defined on 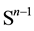to be function 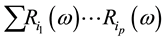for a convex body, where 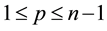and the sum is extended over all increasing sequences of indices chosen from the set.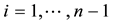

R. Gardner and P. Milanfar [9] provide an algorithm for reconstruction of an origin-symmetric convex body K from the volumes of its projections.

D. Ryabogin and A. Zvavich [10] reconstruct a convex body of revolution from the areas of its shadows by giving a precise formula for the support function.

In this paper, we consider a similar problem posed for the projection curvature radius function of convex bodies. We lead the problem to a system of differential equations of second order on the sphere and solve it applying a consistency method suggested by the author of the article. The solution of the system of differential equations is itself interesting.

Let be a convex body with sufficiently smooth boundary and with positive Gaussian curvature at every point of the boundary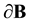. We need some notations.

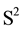―the unit sphere in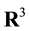,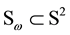―the great circle with pole at,―projection of B onto the plane containing the origin in and orthogonal to,―curvature radius of at the point with outer normal direction and call projection curvature radius of B.

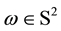Let F be a positive continuously differentiable function defined on the space of “flags”. In this article, we consider:

Problem 1. What are necessary and sufficient conditions for F to be the projection curvature radius function for a convex body?

Problem 2. Reconstruction of that convex body by giving a precise formula for the support function.

Note that one can lead the problem of reconstruction of a convex body by projection curvatures using representation of the support function in terms of mean curvature radius function (see [7] ). The approach of the present article is useful for practical point of view, because one can calculate curvatures of projections from the shadows of a convex body. Let’s note that it is impossible to calculate mean radius of curvature from the limited number of shadows of a convex body. Also let’s note that this is a different approach for such problems, because in the present article we lead the problem to a differential equation of spatial type on the sphere and solve it using a new method (so called consistency method).

The most useful analytic description of compact convex sets is by the support function (see [11] ). The support function of B is defined as

Here denotes the Euclidean scalar product in. The support function of B is positively homogeneous and convex. Below, we consider the support function H of a convex body as a function on (because of the positive homogeneity of H the values on determine H completely).

denotes the space of k times continuously differentiable functions defined on. A convex body B is k-smooth if its support function.

Given a function H defined on, by, we denote the restriction of H onto the circle for, and call the restriction function of H.

Below, we show (Theorem 1) that Problem 1. is equivalent to the problem of existence of a function H defined on such that satisfies the differential equation

(1)

for every.

Definition 1. If for a given F there exists H defined on that satisfies Equation (1), then H is called a solution of Equation (1).

In Equation (1), is a function defined on the space of an ordered pair orthogonal unit vectors, say, (in integral geometry such a pair is a flag and the concept of a flag was first systematically employed by R.V. Ambartzumian in [12] ).

There are two equivalent representations of an ordered pair orthogonal unit vectors, dual each other:

(2)

where is the spatial direction of the first vector, and is the planar direction in coincides with the direction of, while is the spatial direction of the second vector, and is the planar direction in coincides with the direction of. The second representation we will write by capital letters.

Given a flag function, we denote by the image of g defined by

(3)

where (dual each other).

Let G be a function defined on. For every, Equation (1) reduces to a differential equation on the circle.

Definition 2. If is a solution of that equation for every, then G is called a flag solution of Equation (1).

Definition 3. If a flag solution satisfies

(4)

(no dependence on the variable), then G is called a consistent flag solution.

There is an important principle: each consistent flag solution G of Equation (1) produces a solution of Equation (1) via the map

(5)

and vice versa: the restriction functions of any solution of Equation (1) onto the great circles is a consistent flag solution.

Hence, the problem of finding a solution reduces to finding a consistent flag solution.

To solve the latter problem, the present paper applies the consistency method first used in [13] -[15] in an integral equations context.

We denote:―the plane containing the origin of, direction, determines rotation of the plane around Ω,―projection of onto the plane,―curvature radius of at the point with outer normal direction. It is easy to see that

where is dual to.

Note that in the Problem 1. uniqueness (up to a translation) follows from the classical uniqueness result on Christoffel problem, since

(6)

Equation (1) has the following geometrical interpretation.

It is known (see [11] ) that 2 times continuously differentiable homogeneous function H defined on, is convex if and only if

(7)

where is the restriction of H onto.

So in case, it follows from (7), that if H is a solution of Equation (1) then its homogeneous extension is convex.

It is known from convexity theory that if a homogeneous function H is convex then there is a unique convex body with support function H and is the projection curvature radius function of B (see [11] ).

The support function of each parallel shifts (translation) of that body B will again be a solution of Equation (1). By uniqueness, every two solutions of Equation (1) differ by a summand defined on, where. Thus we have the following theorem.

Theorem 1 Let F be a positive function defined on. If Equation (1) has a solution H then there exists a convex body B with projection curvature radius function F, whose support function is H. Every solution of Equation (1) has the form, where, being the support function of the convex body.

The converse statement is also true. The support function H of a 2-smooth convex body B satisfies Equation (1) for, where R is the projection curvature radius function of B (see [16] ).

The purpose of the present paper is to find a necessary and sufficient condition that ensures a positive answer to both Problems 1,2 and suggest an algorithm of construction of the body B by finding a representation of the support function in terms of projection curvature radius function. This happens to be a solution of Equation (1).

Throughout the paper (in particular, in Theorem 2 that follows) we use usual spherical coordinates for points based on a choice of a North Pole and a reference point on the equator. The point with coordinates we will denote by, the points lie on the equator. On we choose anticlockwise direction as positive. On the plane containing we consider the Cartesian x and y-axes where the direction of the y-axis is taken to be the projection of the North Pole onto. The direction of the x-axis we take as the reference direction on and call it the East direction. Now we describe the main result.

Theorem 2 Let B be a 3-smooth convex body with positive Gaussian curvature at every point of and R is the projection curvature radius function of B. Then for chosen as the North pole

(8)

is a solution of Equation (1) for. On we measure from the East direction.

Remark, that the order of integration in the last integral of (8) cannot be changed.

Obviously Theorem 2 suggests a practical algorithm of reconstruction of convex body from projection curvature radius function R by calculation of support function H.

We turn to Problem 1. Let R be the projection curvature radius function of a convex body B. Then necessarily satisfies the following conditions:

a) For every and any reference point on

(9)

This follows from Equation (1), see also [16] .

b) For every direction chosen as the North pole

(10)

where the function F^* is the image of F (see (3)) and is the direction of the y-axis on (Theorem 5).

Let F be a positive 2 times differentiable function defined on. Using (8), we construct a function defined on:

(11)

Note that the last integral converges if the condition (10) is satisfied.

Theorem 3 A positive 2 times differentiable function F defined on represents the projection curvature radius function of some convex body B if and only if F satisfies the conditions (9), (10) and the extension (to) of the function F defined by (11) is convex.

2. The Consistency Condition

We fix and try to solve Equation (1) as a differential equation of second order on the circle. We start with two results from [16] .

a) For any smooth convex domain D in the plane

(12)

where is the support function of D with respect to a point. In (12) we measure from the normal direction at s, is the curvature radius of at the point with normal direction.

b) (12) is a solution of the following differential equation

(13)

One can easy verify that (also it follows from (13) and (12))

(14)

is a flag solution of Equation (1).

Theorem 4 Every flag solution of Equation (1) has the form

(15)

where and are some real coefficients.

Proof of Theorem 4. Every continuous flag solution of Equation (1) is a sum of, where is a flag solution of the corresponding homogeneous equation:

(16)

for every. We look for the general flag solution of Equation (16) in the form of a Fourier series

(17)

After substitution of (17) into (16) we obtain that satisfies (16) if and only if

Now we try to find functions C and S in (15) from the condition that g satisfies (4). We write in dual coordinates i.e. and require that should not depend on for every, i.e. for every

(18)

where was defined in (14).

Here and below denotes the derivative corresponding to right screw rotation around Ω. Differentiation

with use of expressions (see [14] )

(19)

after a natural grouping of the summands in (18), yields the Fourier series of. By uniqueness of

the Fourier coefficients

(20)

where

(21)

3. Averaging

Let H be a solution of Equation (1), i.e. restriction of H onto the great circles is a consistent flag solution of Equation (1). By Theorem 1 there exists a convex body with projection curvature radius function, whose support function is H.

To calculate for a we take Ω for the North Pole of. Returning to the Formula (15) for every we have

(22)

We integrate both sides of (22) with respect to uniform angular measure over to get

(23)

Now the problem is to calculate

(24)

We are going to integrate both sides of (20) and (21) with respect to over. For,

where and we denote

(25)

(26)

Integrating both sides of (20) and (21) and taking into account that

for we get

(27)

i.e. a differential equation for the unknown coefficient.

We have to find given by (24). It follows from (27) that

(28)

Integrating both sides of (5.1) with respect to over we obtain

(29)

Now, we are going to calculate.

It follows from (15) that

(30)

Let be the direction that corresponds to, for. As a point of, let have spherical coordinates with respect to Ω. By the sinus theorem of spherical geometry

(31)

From (31), we get

(32)

Fixing and using (32) we write a Taylor formula at a neighborhood of the point:

(33)

Similarly, for we get

(34)

Substituting (33) and (34) into (30) and taking into account the easily establish equalities

and

(35)

we obtain

(36)

Theorem 5 For every 3-smooth convex body and any direction, we have

(37)

where is the direction of the y-axis on.

Proof of Theorem 5. Using spherical geometry, one can prove that (see also (1))

(38)

where H is the support function of B. Integrating (38), we get

4. A Representation for Support Functions of Convex Bodies

Let be a convex body and. By we denote the support function of B with respect to.

Theorem 6 Given a 2-smooth convex body, there exists a point such that for every chosen as the North pole

(39)

Proof of Theorem 6. For a given B and a point, by we denote the following function defined on

Clearly, is a continuous odd function with maximum:

It is easy to see that for. Since is continuous, so there is a point for which

Let be a direction of maximum now assumed to be unique, i.e.

If the theorem is proved. For the case let O^** be the point for which. It is easy to demonstrate that, hence for a small we find that, contrary to the definition of. So. For the case where there are two or

more directions of maximum one can apply a similar argument.

Now we take the point O^* of the convex body B for the origin of. Below, we will simply denote by H.

By Theorem 6 and Theorem 5, we have the boundary condition (see (36))

(40)

Substituting (29) into (23) we get

(41)

Using expressions (19) and integrating by yields

(42)

where

and

Integrating by parts (42) we get

(43)

Using (34), Theorem 5 and taking into account that

we get

(44)

From (44), using (9) we obtain (8). Theorem 2 is proved.

5. Proof of Theorem 3

Necessity: if F is the projection curvature radius function of a convex body, then it satisfies (9) (see [16] ), the condition (10) (Theorem 5) and F defined by (11) is convex since it is the support function of B (Theorem 2).

Sufficiency: let F be a positive 2 times differentiable function defined on satisfies the conditions (9), (10). We construct the function F on defined by (11). There exists a convex body B with support function F since its extension is a convex function. Also Theorem 2 implies that F is the projection curvature radius of B.

Funding

This work was partially supported by State Committee Science MES RA, in frame of the research project SCS 13-1A244.

References