American Journal of Computational Mathematics
Vol.4 No.3(2014), Article
ID:45995,31
pages
DOI:10.4236/ajcm.2014.43014
Supersonic Flutter of a Spherical Shell Partially Filled with Fluid
Mohamed Menaa, Aouni A. Lakis
Department of Mechanical Engineering, Ecole Poly Technique de Montreal, Montréal, Canada
Email: Aouni.lakis@polymtl.ca
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 November 2013; revised 28 January 2014; accepted 5 February 2014
ABSTRACT
In the present study, a hybrid finite element method is applied to investigate the dynamic behavior of a spherical shell partially filled with fluid and subjected to external supersonic airflow. The structural formulation is a combination of linear spherical shell theory and the classic finite element method. In this hybrid method, the nodal displacements are derived from exact solution of spherical shell theory rather than approximated by polynomial functions. Therefore, the number of elements is a function of the complexity of the structure and it is not necessary to take a large number of elements to get rapid convergence. Linearized first-order potential (piston) theory with the curvature correction term is coupled with the structural model to account for aerodynamic loading. It is assumed that the fluid is incompressible and has no free surface effect. Fluid is considered as a velocity potential at each node of the shell element where its motion is expressed in terms of nodal elastic displacements at the fluid-structure interface. Numerical simulation is done and vibration frequencies are obtained. The results are validated using numerical and theoretical data available in literature. The investigation is carried out for spherical shells with different boundary conditions, geometries, filling ratios, flow parameters, and radius to thickness ratios. Results show that the spherical shell loses its stability through coupled-mode flutter. This proposed hybrid finite element method can be used efficiently for analyzing the flutter of spherical shells employed in aerospace structures at less computational cost than other commercial FEM software.
Keywords:Vibration, Spherical shell, Flutter, Hybrid FEM

1. Introduction
Shells of revolution, particularly spherical shells are one of the primary structural elements in high speed aircraft. Their applications include the propellant tank or gas-deployed skirt of spacecraft. Due to the aerodynamic shape combined with thin wall thicknesses, spherical shells are more disposed to dynamic instability or flutter induced by high Mach number gas flow. It is therefore important to understand the effect of different flow parameters and loadings on their aeroelastic response.
Aeroelastic analysis of shells and plates has been studied by numerous researchers experimentally and analytically [1] . Dowell gives an exhaustive study of the aeroelasticity of shells and plates in his book [2] . After introducing the application of piston theory in the aeroelastic modeling presented by Ashley and Zatarian [3] , a number of interesting experimental and theoretical studies were carried out to investigate supersonic flutter of cylindrical shells. In general, all of this research was concerned with the development of an analytical relation to describe the effect of shell and flow parameters on the critical flutter dynamic pressure. Aeroelastic models in combination with linear or nonlinear piston theory were coupled to the theory of shells to account for fluidstructure interaction. The resulting governing equations were treated numerically using the Galerkin method. A comprehensive experimental test was done by Fung and Olson [4] . They studied the effects of shell boundary conditions and initial stress state due to internal pressure and axial load. It was observed that pressurized cylindrical shell fluttered at a lower level of freestream static pressure than predicted by theory [5] . Later, Evensen and Olson [6] [7] presented a nonlinear analysis to take account of this observed effect. Dowell [8] also analyzed the behavior of a cylindrical shell in supersonic flow for different flow and shell parameters. A complete description of panel flutter modeling is given in his book [2] . A study by Carter and Strearman [9] showed that agreement between the theory and experiments reported in the literature exists in cases that involve a small amount of static preload acting on the shell. Amabili and Pellicano [10] included geometric nonlinearities in their study of supersonic flutter of a circular cylindrical shell. By selecting expansion modes to discretize the aeroelastic equations, they were able to facilitate their solution, and therefore succeeded in capturing the nonlinear behavior of the shell correctly.
There are also some researchers who focused their efforts on the numerical study of this problem. The equations of virtual displacements were solved using the finite elements method. Aeroelastic governing equations were formulated by applying classical shell theory coupled with the piston theory for evaluation of aerodynamic forces. For example, Bismarck-Nasr [11] developed a FEM applied to supersonic flutter of circular shell subjected to internal pressure and axial loading. Ganapathi et al. [12] modeled an orthotropic and laminated anisotropic cylindrical shell in supersonic flow using FEM and analyzed the effect of different shell geometries on the flutter boundaries.
Aeroelasticity of conical shells has also been investigated by few researchers. The leading work in this field was conducted by Shulman [13] . Ueda et al. [14] investigated theoretically and experimentally the supersonic flutter of a conical shell. Dixon and Hudson [15] studied the flutter and vibration of an orthotropic conical shell theoretically. Miserentino and Dixon [16] investigated experimentally the vibration and flutter of a pressurized truncated conical shell. Bismarck-Nasr and Costa-Savio [18] studied the supersonic flutter of conical shells using finite element method. Sunder et al. [18] successfully applied the finite element analysis to calculate the flutter of a laminated conical shell. In another study they found the optimum cone angle in aeroelastic flutter [19] . Mason and Blotter [20] used a finite element technique to find the flutter boundary for a conical shell (a typical rocket nozzle element) subjected to an internal supersonic gas flow. Pidaparti and Yang Henry [21] completed a theoretical study to predict the onset of flutter instability for composites conical shells.
An analytical approach to the supersonic flutter of spherical shell becomes very complicated if one wishes to include different parameters. Therefore, the efficiency of numerical methods such as the finite element method (FEM) is an advantage for cases involving changes to all factors affecting flutter boundaries. The aim of the present study is to develop a hybrid finite element method in order to predict the aeroelastic behavior of isotropic spherical shells with different parameters as boundary conditions, geometries, flow parameters, filling ratios and radius to thickness ratios. The finite element is a spherical frustum instead of the usual rectangular shell element. Linear thin shell theory is coupled with linear piston theory. In the case of a fluid filled shell the effect of dynamic pressure acting on the wall is modeled based on a velocity potential formulation and Bernoulli’s equation. It is assumed that the fluid is incompressible and has no free surface effect. The linear mass, damping and stiffness matrices are obtained. The aeroelastic equation of motion is reduced to a standard eigenvalue problem. The flutter boundary is found by analyzing the real and imaginary parts of the eigenvalues as freestream pressure is varied.
2. Formulation
2.1. Structural Modeling
2.1.1. Equilibrium Equations
In this study the structure is modeled using hybrid finite element method which is a combination of spherical shell theory and classical finite element method. In this hybrid finite element method, the displacement functions are found from exact solution of spherical shell theory rather than approximated by polynomial functions as done in classical finite element method. In the spherical coordinate system (R, θ, ϕ) shown in Figure 1, five out of the six equations of equilibrium derived in reference [22] for spherical shells are written as follows:
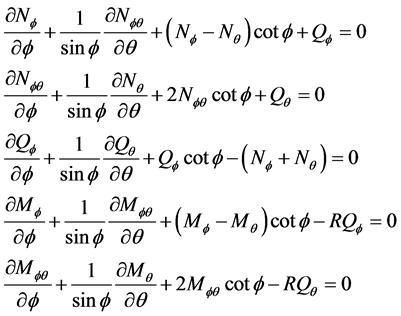 (1)
(1)
where![]() ,
, 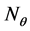 ,
, ![]() are membrane stress resultants; Mϕ, Mθ, Mϕθ the bending stress resultants and Qϕ, Qθ the shear forces (Figure 2). The sixth equation, which is an identity equation for spherical shells, is not presented here.
are membrane stress resultants; Mϕ, Mθ, Mϕθ the bending stress resultants and Qϕ, Qθ the shear forces (Figure 2). The sixth equation, which is an identity equation for spherical shells, is not presented here.
2.1.2. Constitutive Relations
Strains and displacements in axial, ![]() , radial,
, radial, 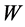 , and circumferential,
, and circumferential, 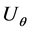 directions are related as follows:
directions are related as follows:
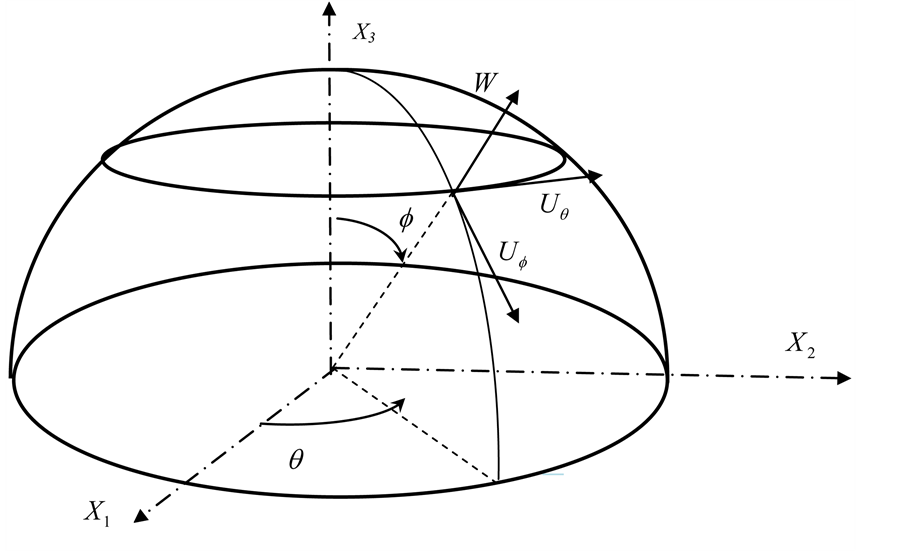
Figure 1. Geometry of the spherical shell.
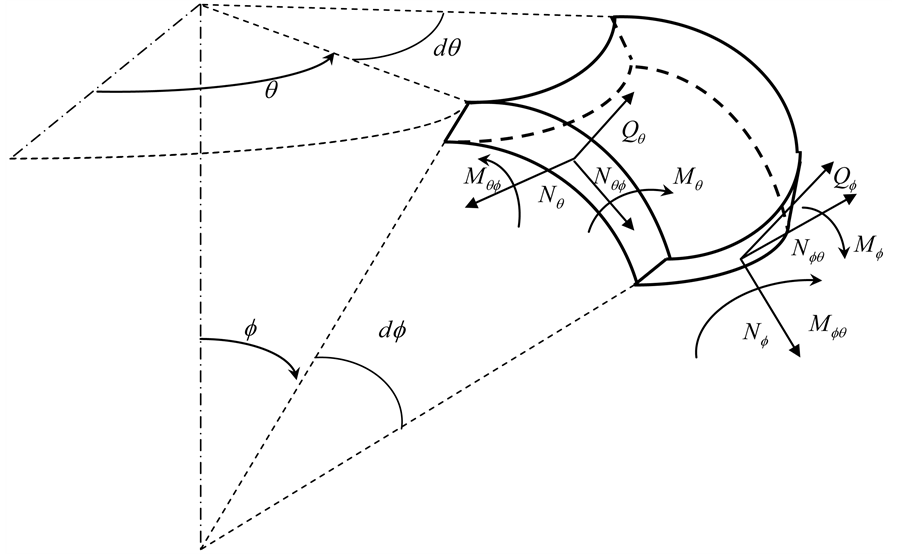
Figure 2. Stress resultants and stress couple.
 (2)
(2)
Displacements ,
,  and
and  in the global Cartesian coordinate system are related to displacements
in the global Cartesian coordinate system are related to displacements![]() ,
,
 And
And ![]() indicated in Figure 3 by:
indicated in Figure 3 by:
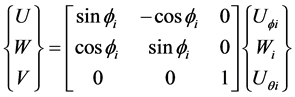 (3)
(3)
The stress vector ![]() is expressed as a function of strain
is expressed as a function of strain ![]() by:
by:
![]() (4)
(4)
where ![]() is the elasticity matrix for an anisotropic shell given by:
is the elasticity matrix for an anisotropic shell given by:
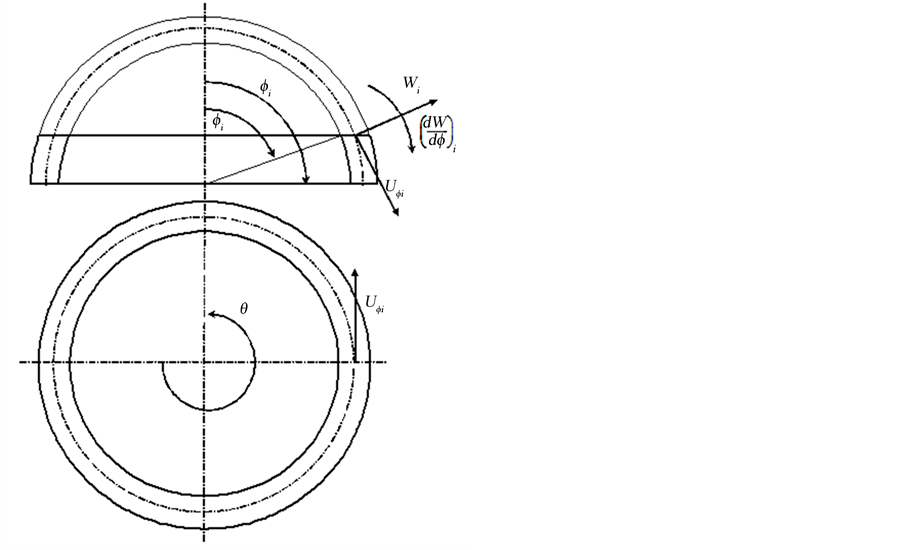
Figure 3. Spheical frustum element.
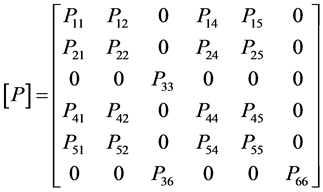 (5)
(5)
Upon substitution of Equations (2), (4) and (5) into Equation (1), a system of equilibrium equations can beobtained as a function of displacements:
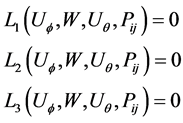 (6)
(6)
These three linear partial differential operators ,
, 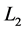 and
and 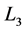 are given in Appendix A, and
are given in Appendix A, and ![]() are elements of the elasticity matrix, which for an isotropic thin shell with thickness h is given by:
are elements of the elasticity matrix, which for an isotropic thin shell with thickness h is given by:
 (7)
(7)
where 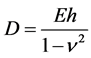 is the membrane stiffness and
is the membrane stiffness and  is the bending stiffness.
is the bending stiffness.
2.1.3. Kinematic Relations
The element is a circumferential spherical frustum shown in Figure 3. It has two nodal circles with four degrees of freedom; axial, radial, circumferential and rotation at each node. This element type makes it possible to use thin shell equations easily to find the exact solution of displacement functions rather than an approximation with polynomial functions as done in classical finite element method.
For motions associated with the circumferential wave number n, we may write:
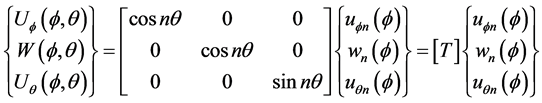 (8)
(8)
The transversal displacement ![]() can be expressed as [22] :
can be expressed as [22] :
 (9)
(9)
where
 (10)
(10)
and where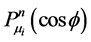 ,
,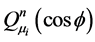 are the associated Legendre functions of the first and second kinds respectively of order n and degree
are the associated Legendre functions of the first and second kinds respectively of order n and degree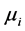 .
.
The expression of the axial displacement uϕν(ϕ) is:
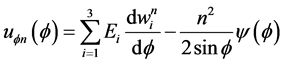 (11)
(11)
where the coefficient Ei is given by:
 (12)
(12)
The auxiliary function ψ is given by the expression:
![]() (13)
(13)
Finally the circumferential displacement uϕν(ϕ) can be expressed as:
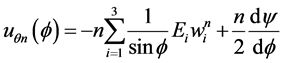 (14)
(14)
The degree 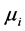 is obtained from the expression
is obtained from the expression
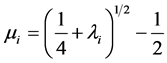 (15)
(15)
where 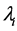 is one the roots of the cubic equation:
is one the roots of the cubic equation:
![]() (16)
(16)
and where
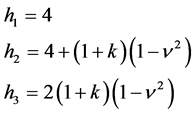 (17)
(17)
with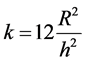 .
.
The above equation has three roots with one real root and two others complex conjugates.
The Legendre functions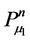 ,
, 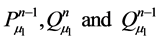 are real functions whereas
are real functions whereas ,
, 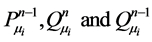
(i = 2, 3) are complex functions. So we can put:
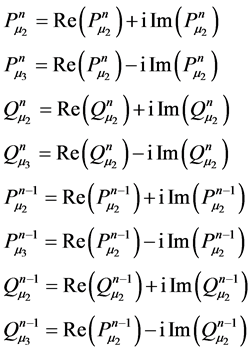 (18)
(18)
Setting
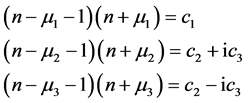 (19)
(19)
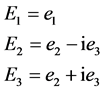 (20)
(20)
Substituting Equations (18), (19) and (20) in Equations (9), (11) and (14) we have:
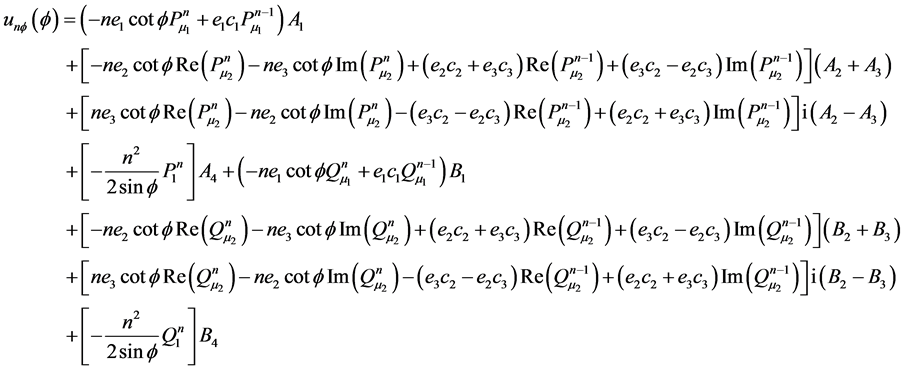
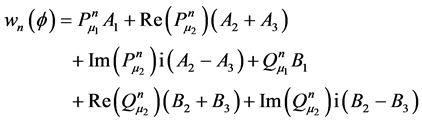 (21)
(21)
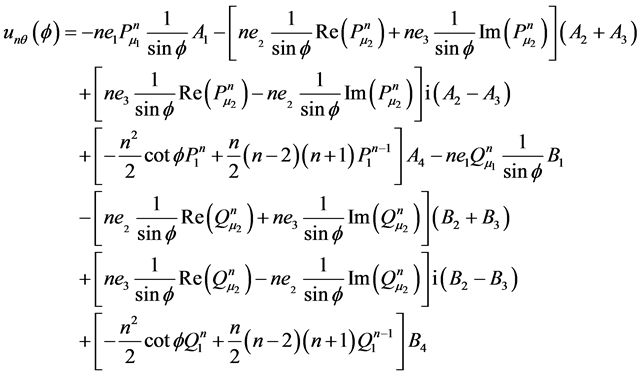
In deriving the above relation we used the recursive relations:
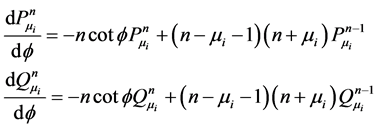 (22)
(22)
Using matrix formulation, the displacement functions can be expressed as follows:
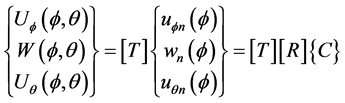 (23)
(23)
The vector ![]() is given by the expression:
is given by the expression:
 (24)
(24)
The elements of matrix ![]() are given in Appendix B.
are given in Appendix B.
In the finite element method, the vector C is eliminated in favor of displacements at elements nodes. At each finite element node, the three displacements (axial, transversal and circumferential) and the rotation are applied. The displacement of node i are defined by the vector:
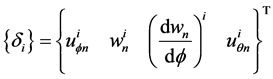 (25)
(25)
The finite element shown in Figure 3 with two nodal lines (i and j) and eight degrees of freedom will have the following nodal displacement vector:
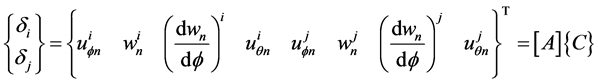 (26)
(26)
with
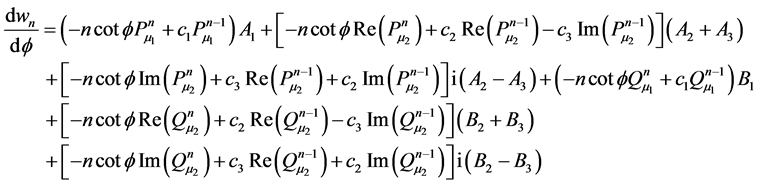 (27)
(27)
The terms of matrix, obtained from the values of matrix ![]() and
and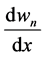 , are given in Appendix B. Now, pre-multiplying Equation (26) by
, are given in Appendix B. Now, pre-multiplying Equation (26) by  one obtains the matrix of the constant Ci as a function of the degree of freedom:
one obtains the matrix of the constant Ci as a function of the degree of freedom:
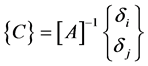 (28)
(28)
Finally, one substitutes the vector ![]() into Equation (26) and obtains the displacement functions as follows:
into Equation (26) and obtains the displacement functions as follows:
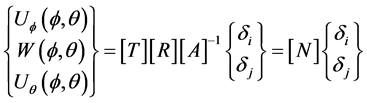 (29)
(29)
The strain vector ![]() can be determined from the displacement functions
can be determined from the displacement functions ![]() and the deformation –displacement equation (2) as:
and the deformation –displacement equation (2) as:
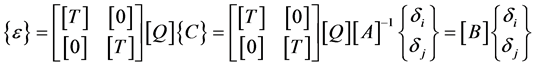 (30)
(30)
where matrix ![]() is given in Appendix C.
is given in Appendix C.
2.1.4. Mass and Stiffness Matrices
This relation can be used to find the stress vector, Equation (4), in terms of the nodal degrees of freedom vector:
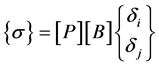 (31)
(31)
Based on the finite element formulation, the local stiffness and mass matrices are:
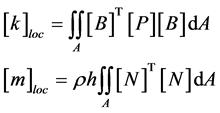 (32)
(32)
where 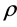 is the density and h is the thickness of shell.
is the density and h is the thickness of shell.
The surface element of the shell wall is ![]() (Figure 2). After integrating over
(Figure 2). After integrating over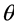 , the preceding equations become
, the preceding equations become
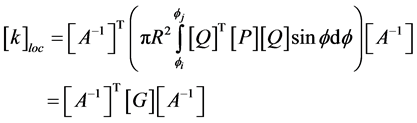
 (33)
(33)
In the global system, the element stiffness and mass matrices are
 (34)
(34)
where
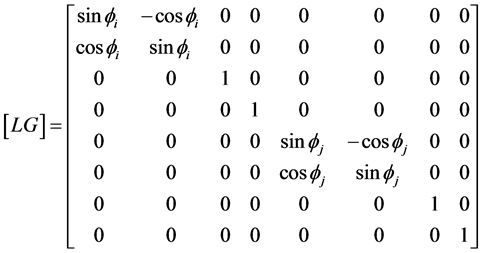 (35)
(35)
From these equations, one can assemble the mass and stiffness matrices for each element to obtain the mass and stiffness matrices for the whole shell: ![]() and
and![]() . Each elementary matrix is 8 × 8, therefore the final dimensions of
. Each elementary matrix is 8 × 8, therefore the final dimensions of ![]() and
and ![]() will be 4*(N + 1) where N is the number of elements of the shell.
will be 4*(N + 1) where N is the number of elements of the shell.
2.2. Aerodynamic Modeling
Piston theory, introduced by Ashley and Zartarian [3] , is a powerful tool for aeroelasticity modeling. In this study the fluid-structure effect due to external pressure loading can be taken into account using linearized firstorder potential theory. This pressure is expressed as:
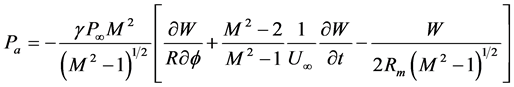 (36)
(36)
where ,
,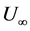 ,
, 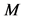 and
and 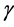 are the freestream static pressure, freestream velocity, Mach number and adiabatic exponent of air respectively. If the Mach number is sufficiently high
are the freestream static pressure, freestream velocity, Mach number and adiabatic exponent of air respectively. If the Mach number is sufficiently high![]() , and curvature term,
, and curvature term,  is neglected, the result is the so-called piston theory:
is neglected, the result is the so-called piston theory:
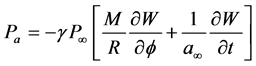 (37)
(37)
where 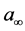 is the free stream speed of sound.
is the free stream speed of sound.
Finally, the aerodynamic pressure in terms of radial displacement is written:
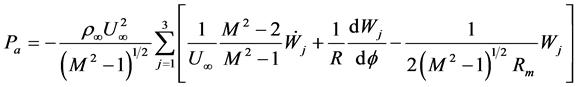 (38)
(38)
and the pressure loading in terms of nodal degrees of freedom is written as:
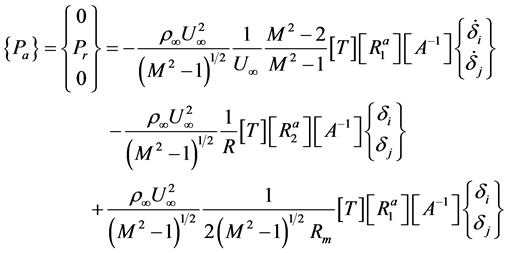
where 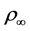 the freestream air density and
the freestream air density and 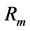 is the median radius for each element. Based on thermodynamic relations the freestream pressure and velocity can be linked together using the following relations:
is the median radius for each element. Based on thermodynamic relations the freestream pressure and velocity can be linked together using the following relations:
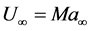 (39)
(39)
 (40)
(40)
The matrix 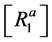 is given by:
is given by:
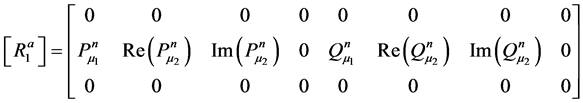 (41)
(41)
The matrix 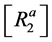 is given by:
is given by:
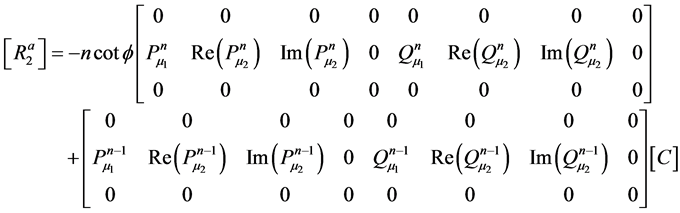 (42)
(42)
where matrix ![]() is given by:
is given by:
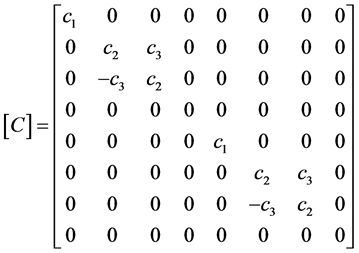 (43)
(43)
The general force vector due to a pressure field is written as:
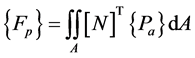 (44)
(44)
The local damping matrix is given by:
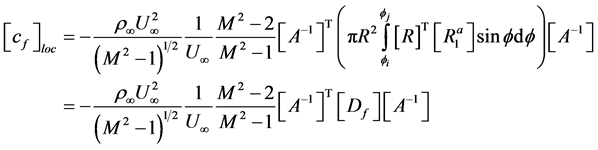 (45)
(45)
Finally the local stiffness matrix is given by:
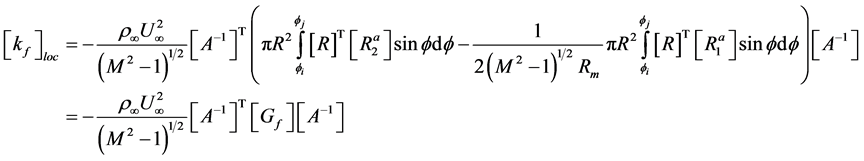
In the global system, the element damping and stiffness matrices are:
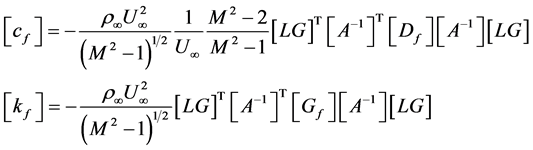 (46)
(46)
From these equations, one can assemble the damping and stiffness matrices for each element to obtain the damping and stiffness matrices for the whole shell:  and
and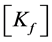 .
.
2.3. Fluid Modeling
The Laplace equation satisfied by velocity potential for inviscid, incompressible and irrotational fluid in the spherical system is written as:

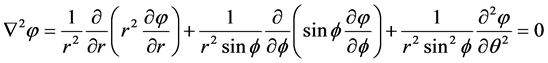 (47)
(47)
where the velocity components are:
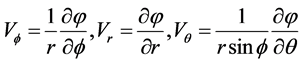 (48)
(48)
Using the Bernouilli equation, hydrodynamic pressure in terms of velocity potential 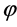 and fluid density
and fluid density ![]() is found as:
is found as:
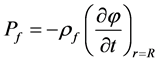 (49)
(49)
The impermeability condition, which ensures contact between the shell surface and the peripheral fluid, is written as:
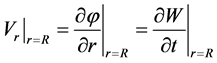 (50)
(50)
with
 (51)
(51)
Method of separation of variables for the velocity potential solution can be done as follows:
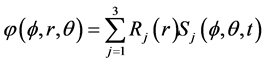 (52)
(52)
Placing this relation into the impermeability condition (50), we can find the function ![]() in term of radial displacement:
in term of radial displacement:
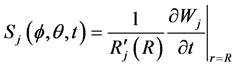 (53)
(53)
Hence the equation becomes
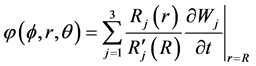 (54)
(54)
With substitution of the above equation into Laplace Equation (47), the following second order equation in terms of ![]() is obtained
is obtained
 (55)
(55)
Solution of the above differential equation yields the following:
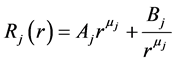 (56)
(56)
For internal flow ![]()
Finally, the hydrodynamic pressure in terms of radial displacement is written:
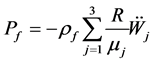 (57)
(57)
We put:
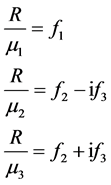 (58)
(58)
And the pressure loading in terms of nodal degrees of freedom is written as:
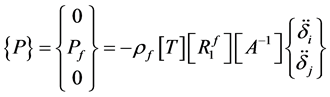 (59)
(59)
where matrix 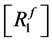 is given by:
is given by:
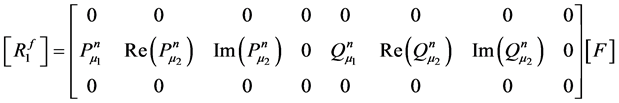 (60)
(60)
where ![]() is expressed as:
is expressed as:
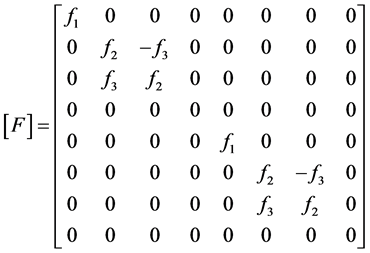 (61)
(61)
The general force vector due the fluid pressure loading is given by:
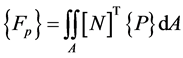 (62)
(62)
After substituting for pressure field vector and matrix ![]() in the above equation, the local matrix
in the above equation, the local matrix 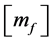 can be found from the following:
can be found from the following:
 (63)
(63)
In the global system the element stiffness and mass matrices are
 (64)
(64)
From these equations, one can assemble the mass for each element to obtain the mass matrix for the whole shell: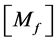 .
.
The governing equation which accounts for fluid-shell interaction in the presence external supersonic airflow is derived as:
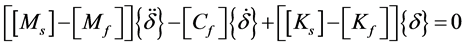 (65)
(65)
where subscripts s and f refer to shells in vacuo and fluid respectively.
3. Eigenvalue Problem
The global fluid matrices mentioned in Equation (65) may be obtained, respectively, by superimposing the mass, damping and stiffness matrices for each individual fluid finite element. After applying the boundary conditions the global matrices are reduced to square matrices of order 4*(N + 1) − J, where N is the number of finite elements in the shell and J is the number of constraints applied. Finally, the eigenvalue problem is solved by means of the equation reduction technique. Equation (65) may be rewritten as follows:
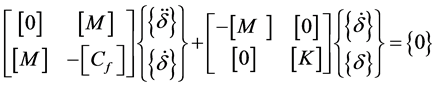 (66)
(66)
where
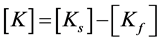
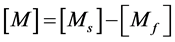
![]() is the global displacement vector.
is the global displacement vector.  and
and 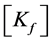 represent damping and elastic forces induced by the flowing fluid.
represent damping and elastic forces induced by the flowing fluid. 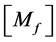 is added fluid mass. The eigenvalue problem is given by:
is added fluid mass. The eigenvalue problem is given by:
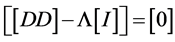 (67)
(67)
where
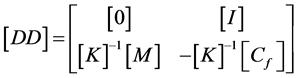
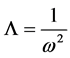 and
and ![]() is the identity matrix.
is the identity matrix.
An in house computer code based on the finite element method was developed as part of this work to establish the structural and fluid matrices of each element based on equations developed using the theoretical approach. The calculations for each finite element are performed in two stages: the first dealing with solid shell and the second with the effect of the flowing fluid. Aeroelastic stability will be examined by studying the eigenvalues in the complex plane. When the imaginary part of ω becomes negative the amplitude of the shell motion grows exponentially with time, thus indicating dynamic instability. The flutter boundary is obtained numerically by tracing the eigenvalues to see when the sign of imaginary part just changes from positive to negative. For the fixed value of circumferential wave number n, the onset of instability is determined by varying the value of freestream static pressure. This procedure is repeated for different values of n until the minimum critical pressure is obtained.
4. Results and Discussion
In this section numerical results are presented and compared with existing experimental, analytical and numerical data.
4.1. Validation and Comparison
For the cases investigated in the present paper, the predicted dimensionless frequencies are expressed by the following relation:
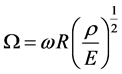 (68)
(68)
where:
 is the natural angular frequency,
is the natural angular frequency,
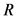 is the radius of the reference surface,
is the radius of the reference surface,
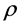 is the density, and
is the density, and
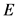 is the modulus of elasticity.
is the modulus of elasticity.
Results for different boundary conditions, geometries, flow parameters and radius to thickness ratios compared to experimental, theoretical and numerical analyses are presented (see Figure 4).
4.1.1. Spherical Shells in Vacuo
Case 1: clamped spherical shell with  = 10˚
= 10˚
Narassihan and Alwar [23] investigated the case of an axisymmetric clamped spherical shell. The analysis is based on the application of the Chebyshev-Galerkin spectral method for the evaluation of free vibration frequencies and mode shapes. Sai Ram and Sreedhar Babu [24] analyzed the same case with the classical finite element method using 80 elements. Each element is an eight nodded degenerated is oparametric shell element with nine degrees of freedom at each node. With our model and using 6 finite elements, the natural frequencies were computed; the results are shown in Table1
Case 2: clamped spherical shell with 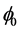 = 30˚
= 30˚
This case was investigated analytically by Kalnins [25] using classical theory and transverse vibration theory. With our theory, we used 8 finite elements to study the spherical shell with the results shown in Table2 The frequencies we obtained with our model are very comparable to Kalinin’s values.
Case 3: spherical shell with 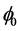 = 60˚ under two boundary conditions: clamped, simply supported
= 60˚ under two boundary conditions: clamped, simply supported

Figure 4. Definition of angle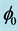 .
.
Free axisymmetric vibration of the spherical shell in this case was studied by Kalnins [26] , Cohen [27] , Navaratna [28] , Webster [29] , Greene et al. [30] , Tessler and Spiridigliozzi [31] , Gautham and Ganesan [32] and Buchanan and Rich [33] . In the present investigation, the shell was investigated with 10 elements; the results are given respectively for clamped, simply supported hemispherical shells in Table 3 and Table4
Case 4: spherical shell with 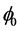 = 90˚
= 90˚
Kraus [22] investigated the case of simply supported spherical shell using a general theory, which included the effects of transverse shear stress and rotational inertia. For cases both with and without these effects, he determined the natural frequencies for the shell motion that was independent of 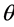 for circumferential mode number
for circumferential mode number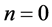 . Tessler and Spiridigliozzi [31] , Gautham and Ganesan [34] analyzed the case of clamped hemispherical shell. Ventsel et al. [35] studied the case of simply supported spherical shell using the boundary elements method for various circumferential mode numbers
. Tessler and Spiridigliozzi [31] , Gautham and Ganesan [34] analyzed the case of clamped hemispherical shell. Ventsel et al. [35] studied the case of simply supported spherical shell using the boundary elements method for various circumferential mode numbers![]() . With our model and using 12 finite elements, the natural frequencies were computed for clamped and simply supported shells. The results are shown respectively in Table 5 and Table6
. With our model and using 12 finite elements, the natural frequencies were computed for clamped and simply supported shells. The results are shown respectively in Table 5 and Table6
4.1.2. Flutter of Spherical Shells
The problem treated for validation is the flutter boundary of a simply–supported spherical shell subjected to external supersonic airflow. As there is no information available for flutter of spherical shells, this case has been compared with simply-supported cone studied by various authors. The conical shell has the following data: Young’s Modulus, E = 6.5 106 lb-in-2, Poisson’s ratio, ν = 0.29, material mass density, ρ = 8.33 10-4 lb-s2-in-4, shell thickness, h = 0.051 in, cone semi-vertex angle α = 5˚. The supersonic airflow has freestream Mach number, M∞ = 3, stagnation temperature, T∞ = 288.15 K. The results are shown in Table 7 where 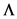 is the dynamic pressure parameter defined as:
is the dynamic pressure parameter defined as:
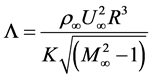 (69)
(69)
where 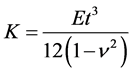 is the bending stiffness.
is the bending stiffness.
When results are summarized and compared with other finite element and analytical solutions, this method shows good convergence using only 15 elements with small disagreements. It should be noted that the previous analytical methods [13] [15] use Donnel-Mushtari simplified shell theory while [14] uses Novozhilov’s thin shell with the different method of application of finite element solution. On the other hand, a complete form of the linear piston theory is used by [21] as in the present study and the results are very close; but the expression used by Dixon and Hudson [15] , Ueda et al. [14] for the piston theory does not have a curvature term which has caused greater differences in the results.
4.2. Flutter Boundary
Flutter which is observed in all the papers using piston theory is a coupled-mode flutter. Indeed, let us consider motion of the shell eigenvalues in the complex ω plane. If the freestream pressure is not very high, and the shell is stable, all complex frequencies are located in the top ω half-plane. Let us now increase freestream pressure. The first and the second complex frequencies move toward each other, almost merge, and then go away from
Table 5. Normalized natural frequencies for 90˚ clamped spherical shell with R/h = 10.
each other in vertical directions (Figure 5). Thus, interaction of two modes occurs. Physically this interaction of the shell modes happens through the effect of the air flow.
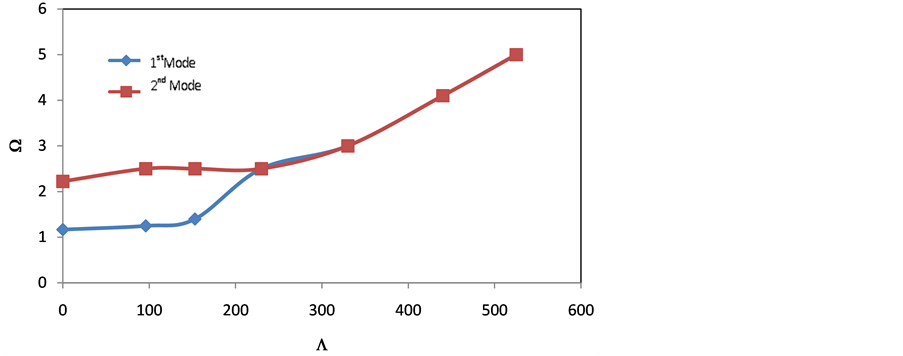
A simply supported spherical shell with 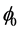 = 30˚ is treated here. The complex frequencies only for the first and second modes versus freestream dynamic pressure are plotted in Figure 6. Aerodynamic pressure is evaluated using Equation (36). In Figure 6(a) the real part of the complex frequency increases for the first mode while for the second mode it decreases as the freestream dynamic pressure parameter
= 30˚ is treated here. The complex frequencies only for the first and second modes versus freestream dynamic pressure are plotted in Figure 6. Aerodynamic pressure is evaluated using Equation (36). In Figure 6(a) the real part of the complex frequency increases for the first mode while for the second mode it decreases as the freestream dynamic pressure parameter  increases. For higher
increases. For higher
Table 7. Comparison of critical dynamical pressure parameter (simply supported case).
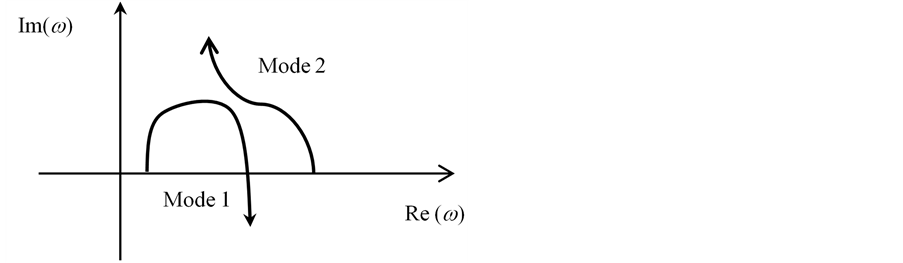
Figure 5. Trajectories of the complex frequencies loci in the complex ω plane during the changing of the dynamic pressure.
values of dynamic pressure these real parts, representing the oscillation frequency, eventually coalesce into a single mode. Further increasing the dynamic pressure of the flow causes the shell to lose its stability at 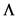 cr = 410. This instability is due to coupled-mode flutter where the imaginary part of complex frequency (representing the damping term of the aeroelastic system) becomes zero for certain critical pressure (Figure 6(b)).
cr = 410. This instability is due to coupled-mode flutter where the imaginary part of complex frequency (representing the damping term of the aeroelastic system) becomes zero for certain critical pressure (Figure 6(b)).
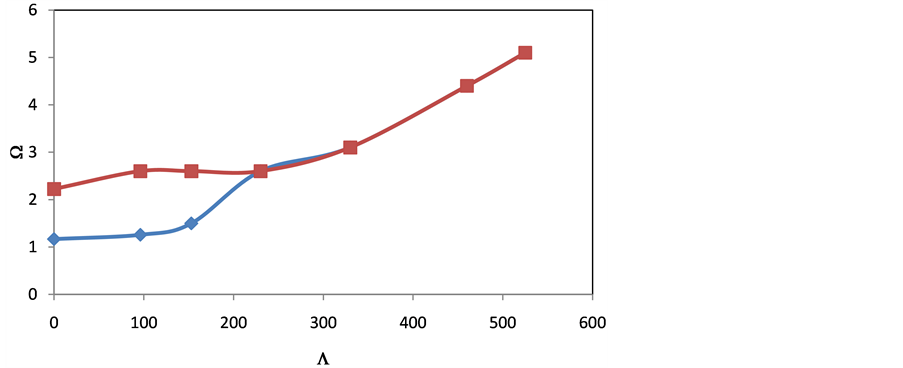
The same behaviour is observed by real and imaginary parts of complex frequencies as the static pressure increases (Figure 7) but the onset of flutter is at 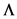 cr = 410 if the freestream static pressure is evaluated using Equation (37). Prediction of the critical freestream static pressure using Equation (36) provides approximately the same results when evaluating the pressure field using Equation (37). As expected, using the piston theory with the correction term to account for shell curvature produces a better approximation for the pressure loading acting on a curved shell exposed to supersonic flow.
cr = 410 if the freestream static pressure is evaluated using Equation (37). Prediction of the critical freestream static pressure using Equation (36) provides approximately the same results when evaluating the pressure field using Equation (37). As expected, using the piston theory with the correction term to account for shell curvature produces a better approximation for the pressure loading acting on a curved shell exposed to supersonic flow.
In Figure 8 the onset of flutter for different angles is plotted. By increasing the angle , flutter instability occurs at lower pressure. This decrease in
, flutter instability occurs at lower pressure. This decrease in  cr with
cr with 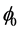 is attributed to the fact that the natural frequencies always decrease as the angle
is attributed to the fact that the natural frequencies always decrease as the angle 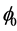 is increased.
is increased.
The effect of radius to thickness ratio R/h is presented in Figure 9. This figure shows an increase of  cr with an increase of radius to thickness ratio. This increase in
cr with an increase of radius to thickness ratio. This increase in  cr is attributed to the fact that the mass of shell is greater when the shell is thick, and the effect of pressure is less important for a thick shell than for a thin shell. On the other hand, when the shell is thin it becomes unstable at higher dynamical pressure levels due to an increase in stiffness because of a decrease in thickness. The same conclusion is reported in [12] for the flutter of
cr is attributed to the fact that the mass of shell is greater when the shell is thick, and the effect of pressure is less important for a thick shell than for a thin shell. On the other hand, when the shell is thin it becomes unstable at higher dynamical pressure levels due to an increase in stiffness because of a decrease in thickness. The same conclusion is reported in [12] for the flutter of
 (a)
(a)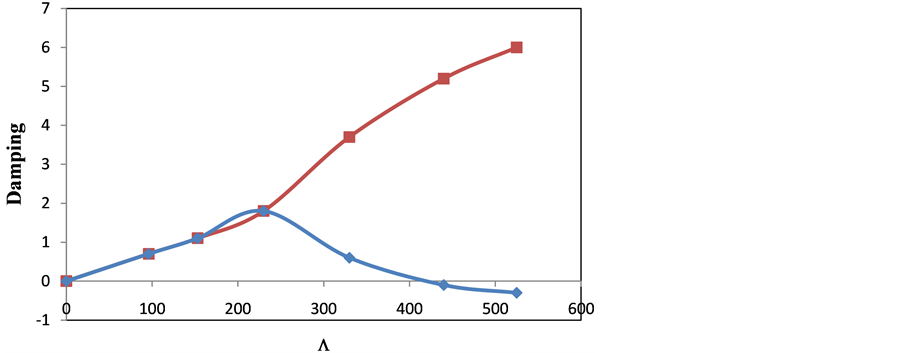 (b)
(b)
Figure 6. (a) Real part and (b) imaginary part of the complex frequencies versus the freestream static pressure parameter; static pressure evaluated by Equation (36).
cylindrical shells.
In order to study the effect of filling ratio, Figure 10 shows the critical value of freestream static pressure for different filling ratios, H/R. Shell geometry and flow parameters are the same as the previous case study with liquid filled density ρf =9.355 × 10-5lb s2 in-4. It is seen that the value of critical dynamic pressure parameter decreases as the filling ratio increases from a low value. This rapid change in critical dynamic pressure at low filling ratios and its almost steady behaviour at large filling ratios indicates that the fluid near the bottom of the shell is largely influenced by elastic deformation when a shell is subjected to external supersonic flow.
The effect of boundary conditions on the flutter onset is presented in Table8 It is seen that for freely simply supported ends, v = w = 0, flutter onset occurs at  = 510.5 which indicates more flutter resistance compared to simply supported or clamped ends. It is indicated that there is no difference for flutter onset when the shell is either clamped or simply supported. We obtained the same results in the conical shells subjected to supersonic flow.
= 510.5 which indicates more flutter resistance compared to simply supported or clamped ends. It is indicated that there is no difference for flutter onset when the shell is either clamped or simply supported. We obtained the same results in the conical shells subjected to supersonic flow.
5. Conclusion
An efficient hybrid finite element method is presented to investigate the aeroelastic stability of an empty or partially liquid filled spherical shell subjected to external supersonic flow. Linear shell theory is coupled with first order piston theory to account for aerodynamic pressure. The effect of curvature correction in piston theory was
 (a)
(a)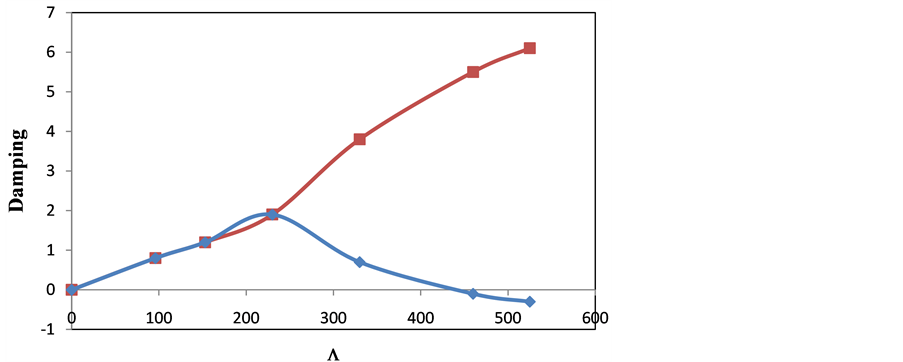 (b)
(b)
Figure 7. (a) Real part and (b) imaginary part of the complex frequencies versus the freestream static pressure parameter; static pressure evaluated by Equation (37).
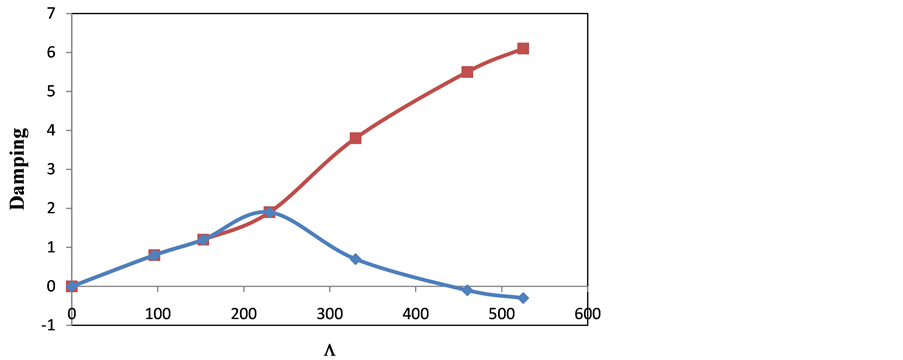
Figure 8. Variation of the critical freestream static pressure parameter with angle 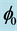 for simply supported shell.
for simply supported shell.
Figure 9. Variation of the critical freestream static pressure parameter with R/h for simply supported shell.

Figure 10. Variation of the critical freestream static pressure parameter with R/H for simply supported shell.
analyzed. Fluid structure interaction due to hydrodynamic pressure of internal fluid is also taken into account. The study has been done for shells with various geometries, radius to thickness ratios, filling ratios and boundary conditions. In all study cases one type of instability is found; coupled-mode flutter in the first and second mode. Increasing the radius to thickness ratio leads the onset of flutter to occur at higher dynamic pressure. Decreasing the angle  of the spherical shell causes the flutter boundary to occur at lower dynamic pressure. A lower filling ratio has more flutter resistance than a higher filling ratio. The proposed hybrid finite element formulation can give reliable results at less computational cost compared to commercial software since the latter imposes some restrictions when such analysis is done.
of the spherical shell causes the flutter boundary to occur at lower dynamic pressure. A lower filling ratio has more flutter resistance than a higher filling ratio. The proposed hybrid finite element formulation can give reliable results at less computational cost compared to commercial software since the latter imposes some restrictions when such analysis is done.
References
- Bismarck-Nasr, M.N. (1996) Finite Elements in Aeroelasticity of Plates and Shells. Applied Mechanics Reviews Journal, 49, S17-S24. http://dx.doi.org/10.1115/1.3101970
- Dowell, E.H. (1975) Aeroelasticity of Plates and Shells. Noordhoff International Publishing, Leyden.
- Ashley, H. and Zartarian, G. (1956) Piston Theory—New Aerodynamic Tool for Aeroelastician. Journal of the Aeronautical Sciences, 23, 1109-1118. http://dx.doi.org/10.2514/8.3740
- Fung, Y.C. and Olson, M.D. (1966) Supersonic Flutter of Circular Cylindrical Shells Subjected to Internal Pressure and Axial Compression. AIAA Journal, 4, 858-864. http://dx.doi.org/10.2514/3.3558
- Fung, Y.C. and Olson, M.D. (1967) Comparing Theory and Experiment for Supersonic Flutter of Circular cylindrical shells. AIAA Journal, 5, 1849-1856. http://dx.doi.org/10.2514/3.4315
- Evensen, D.A. and Olson, M.D. (1967) Nonlinear Flutter of a Circular Cylindrical Shell in Supersonic Flow. NASA Technical Note, NASA TN D-4265.
- Evensen, D.A. and Olson, M.D. (1968) Circumferentially Traveling Wave Flutter of Circular Cylindrical Shell. AIAA Journal, 6, 1522-1527. http://dx.doi.org/10.2514/3.4799
- Dowell, E.H. (1966) Flutter of Infinitely Long Plates and Shells. II-Cylindrical Shell. AIAA Journal, 4, 1510-1518. http://dx.doi.org/10.2514/3.3728
- Carter, L.L. andStearman, R.O. (1968) Some Aspects of Cylindrical Panel Flutter. AIAA Journal, 6, 37-43. http://dx.doi.org/10.2514/3.4438
- Amabili, M. and Pellicano, F. (2001) Nonlinear Supersonic Flutter of Circular Cylindrical shells. AIAA Journal, 39, 564-573. http://dx.doi.org/10.2514/2.1365
- Bismarck-Nasr, M.N. (1976) Finite Element Method Applied to the Supersonic Flutter of Circular Cylindrical Shells. International Journal for Numerical Methods in Engineering, 10, 423-435. http://dx.doi.org/10.1002/nme.1620100212
- Ganapathi, M., Varadan, T.K. and Jijen, J. (1994) Field Consistent Element Applied to Flutter Analysis of Circular Cylindrical Shells. Journal of Sound and Vibration, 171, 509-527. http://dx.doi.org/10.1006/jsvi.1994.1137
- Shulman, Y. (1959) Vibration and Flutter of Cylindrical and Conical Shells. MIT ASRL Rept. 74-2 OSR Technical Report, 59-776.
- Ueda, T., Kobayashi, S. and Kihira, M. (1977) Supersonic Flutter of Truncated Conical Shells. Transactions of the Japan Society for Aeronautical and Space Sciences, 20, 13-30.
- Dixon, S.C. and Hudson M.L. (1970) Flutter, Vibration and Buckling of Truncated Orthotropic Conical Shells with Generalized Elastic Edge Restraint. NASA TN D-5759.
- Miserento, R. and Dixon S.C. (1971) Vibration and Flutter Tests of a Pressurized Thin walled Truncated Conical Shell. NASA TN D-6106.
- Bismarck-Nasr, M.N and Costa Savio, H.R. (1979) Finite Element Solution of the Supersonic Flutter of Conical Shells. AIAA Journal, 17, 1148-1150. http://dx.doi.org/10.2514/3.61291
- Sunder, P.J., Ramakrishnan, V.C. and Sengupta, S. (1983) Finite Element Analysis of 3-ply Laminated Conical Shell for Flutter. International Journal for Numerical Methods in Engineering, 19, 1183-1192. http://dx.doi.org/10.1002/nme.1620190806
- Sunder, P.J., Ramakrishnan, V.C. and Sengupta, S. (1983) Optimum Cone Angles in Aeroelastic Flutter, Computer and Structures, 17, 25-29. http://dx.doi.org/10.1016/0045-7949(83)90024-X
- Mason, D.R and Blotter P.T. (1986) Finite Element Application to Rocket Nozzle Aeroelasticity. Journal of Propulsion and Power, 2, 499-507. http://dx.doi.org/10.2514/3.22933
- Pidaparti, R.M.V. and Yang Henry, T.Y. (1993) Supersonic Flutter Analysis of Composite Plates and Shells. AIAA Journal, 31, 1109-1117. http://dx.doi.org/10.2514/3.11735
- Kraus, H. (1967) Thin Elastic Shell. John Wiley and Sons, New York.
- Narasimhan, M.C. and Alwar, R.S. (1992) Free Vibration Analysis of Laminated Orthotropic Spherical Shell. Journal of Sound and Vibration, 54, 515-529. http://dx.doi.org/10.1016/0022-460X(92)90783-T
- Sai Ram, K.S. and Sreedhar Babu, T. (2002) Free Vibration of Composite Spherical Shell Cap with and Without a Cutout. Computers and Structures, 80, 1749-1756. http://dx.doi.org/10.1016/S0045-7949(02)00210-9
- Kalnins, A. (1961) Free Non-Symmetric Vibrations of Shallow Spherical Shells. Journal of the Acoustical Society of America, 33, 1102-1107. http://dx.doi.org/10.1121/1.1908908
- Kalnins, A. (1964) Effect of Bending on Vibration of Spherical Shell. Journal of the Acoustical Society of America, 36 74-81. http://dx.doi.org/10.1121/1.1918916
- Cohen, G.A. (1965) Computer Analysis of Asymmetric Free Vibrations of Ring Stiffened Orthotropic Shells of Revolution. AIAA Journal, 3, 2305-2312. http://dx.doi.org/10.2514/3.3360
- Navaratna, D.R. (1966) Natural Vibration of Deep Spherical Shells. AIAA Journal, 4, 2056-2058. http://dx.doi.org/10.2514/3.3847
- Webster, J.J. (1967) Free Vibrations of Shells of Revolution Using Ring Finite Elements. International Journal of Mechanical Sciences, 9, 559-570. http://dx.doi.org/10.1016/0020-7403(67)90055-0
- Greene, B.E., Jones, R.E., Mc Lay, R.W. and Strome, D.R. (1968) Dynamic Analysis of Shells Using Doubly Curved Finite Elements. Proceedings of the Second Conference on Matrix methods in Structural Mechanics, TR-68-150, 185-212.
- Tessler, A. and Spiridigliozzi, L. (1988) Resolving Membrane and Shear Locking Phenomena in Curved Deformable Axisymmetric Shell Element. InternationalJournal for Numerical Methods in Engineering, 26, 1071-1080. http://dx.doi.org/10.1002/nme.1620260506
- Gautham, B.P. and Ganesan, N. (1992) Free Vibration Analysis of Thick Spherical Shells. Computers and Structures, 45, 307-313. http://dx.doi.org/10.1016/0045-7949(92)90414-U
- Buchanan, G.R. and Rich, B.S. (2002) Effect of Boundary Conditions on Free Vibrations of Thick Isotropic Spherical Shells. Journal of Vibration and Control, 8, 389-403. http://dx.doi.org/10.1177/107754602023688
- Gautham, B.P. and Ganesan, N. (1997) Free Vibration Characteristics of Isotropic and Laminated Orthotropic Shell Caps. Journal of Sound and Vibration, 204, 17-40. http://dx.doi.org/10.1006/jsvi.1997.0904
- Ventsel, E.S, Naumenko, V., Strelnikova, E. and Yeseleva, E. (2010) Free Vibrations of Shells of Revolution Filled With Fluid. Journal of Engineering Analysis with Boundary Elements, 34, 856-862. http://dx.doi.org/10.1016/j.enganabound.2010.05.004
Appendix A: Expressions for Equation (6)
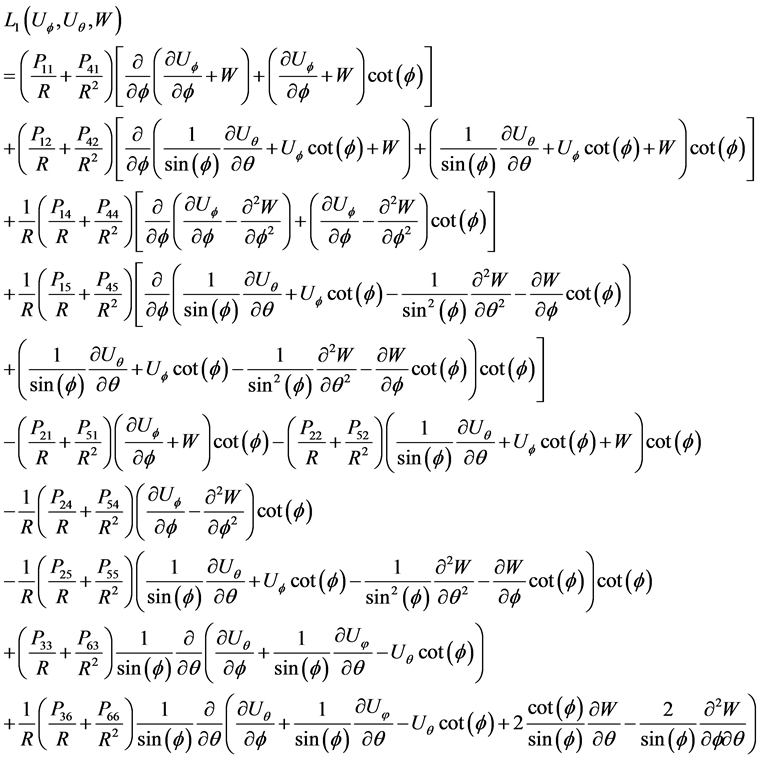
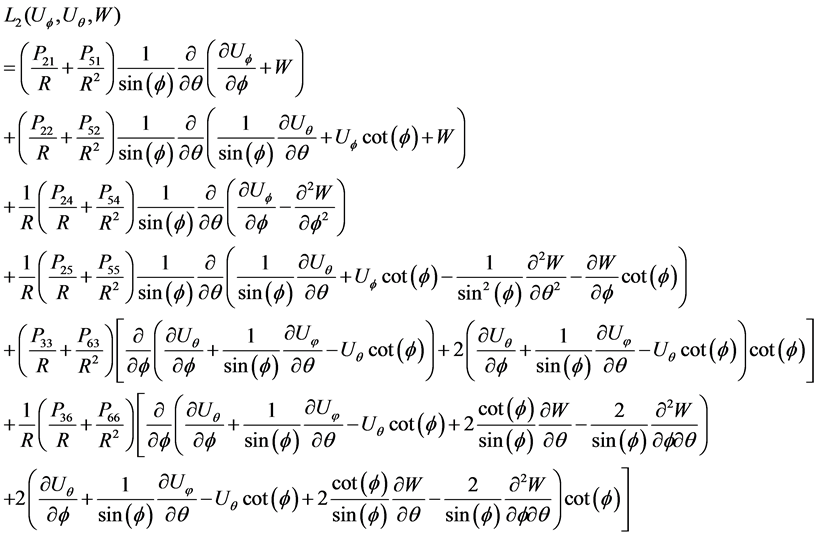
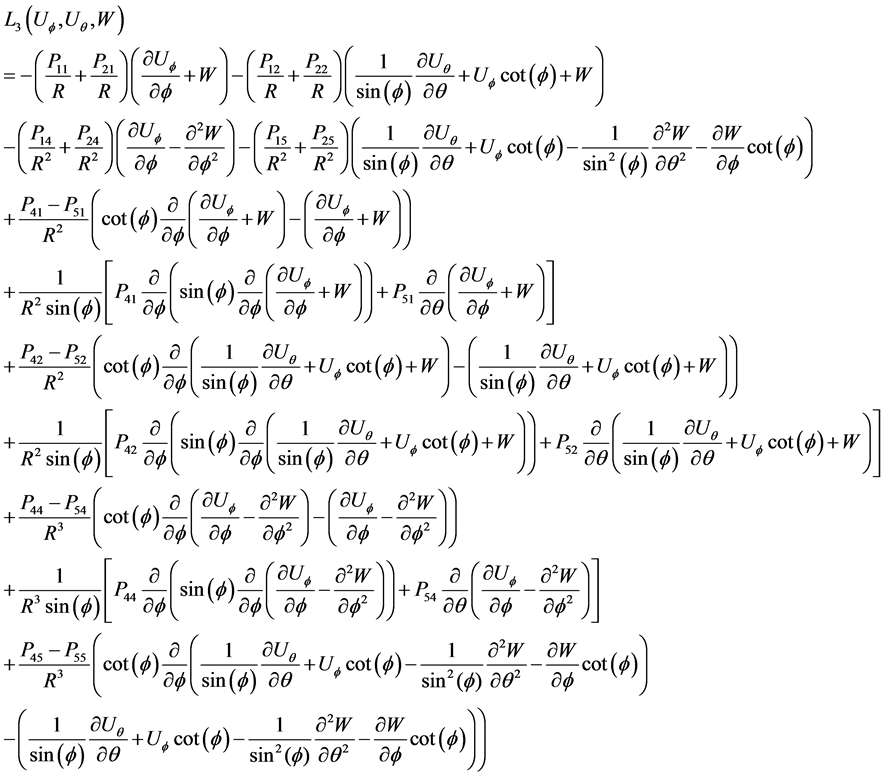

Appendix B: Elements of Matrices R and A
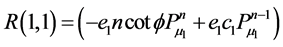

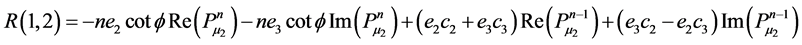
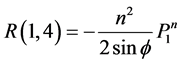
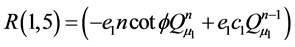

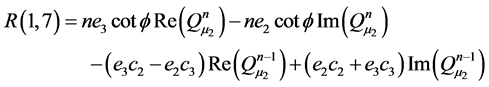
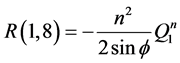
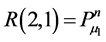
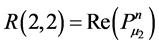
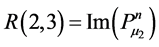
![]()
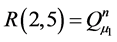

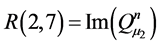
![]()
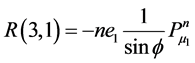
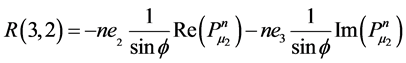
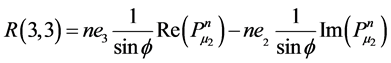

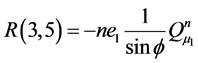

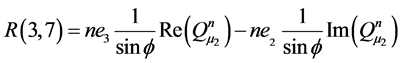
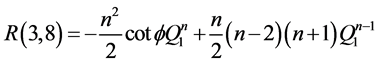
![]() ,
,![]() ,
,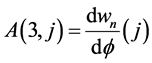 ,
,![]() with
with ,
,![]() ,
, ![]() ,
, 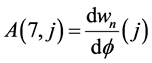 ,
, ![]() with
with 
![]()
Appendix C: Elements of Matrix Q

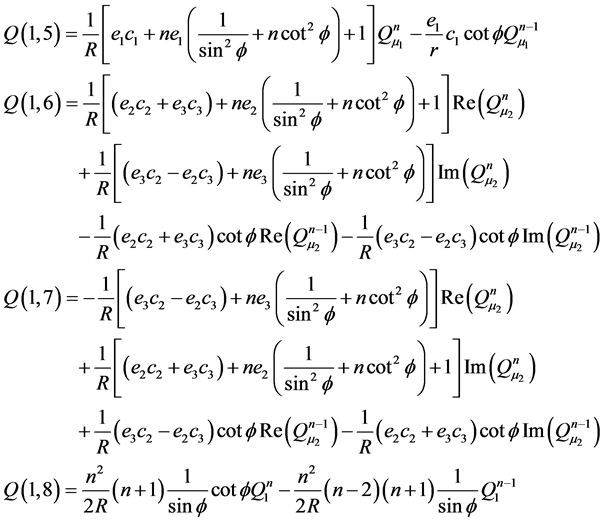
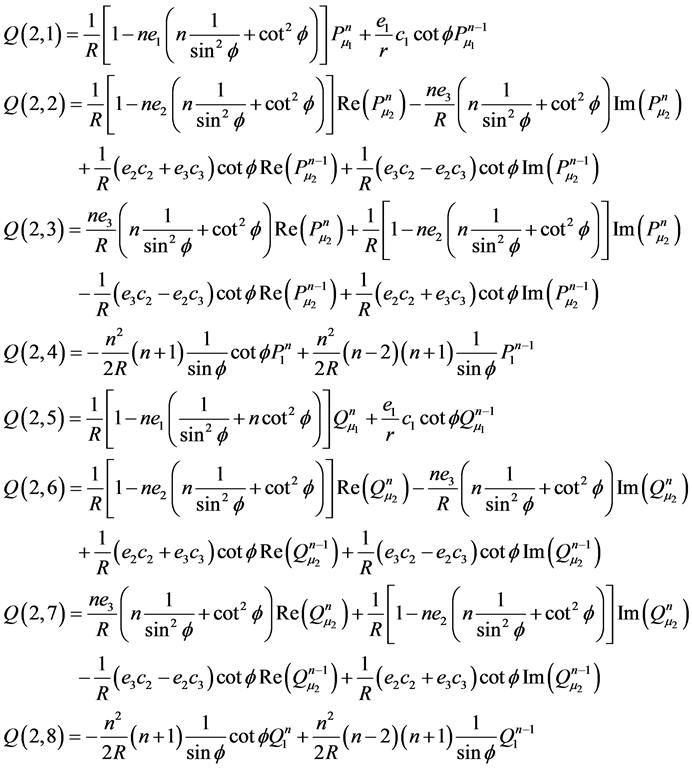
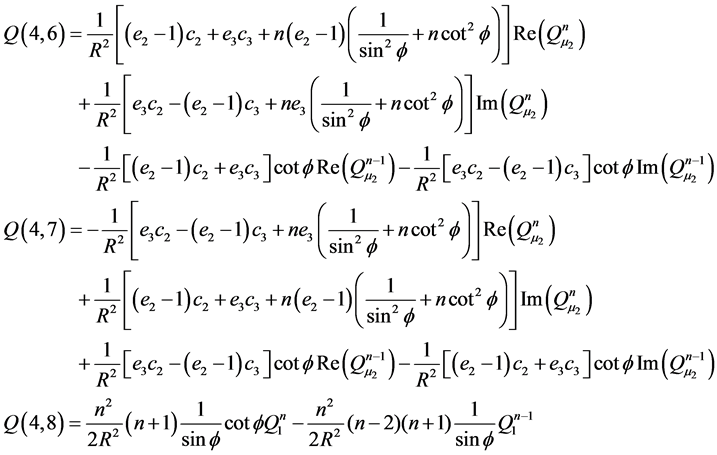
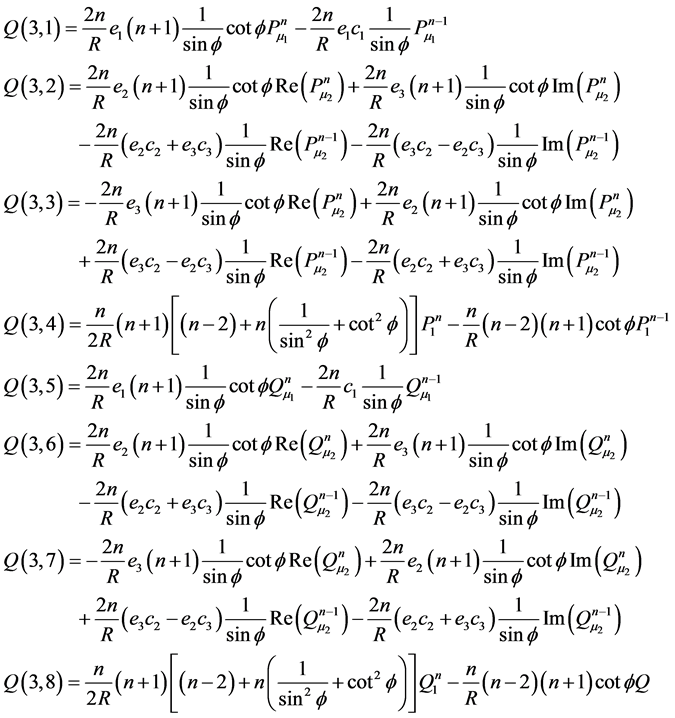
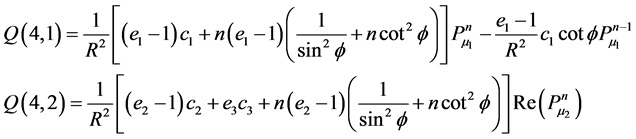
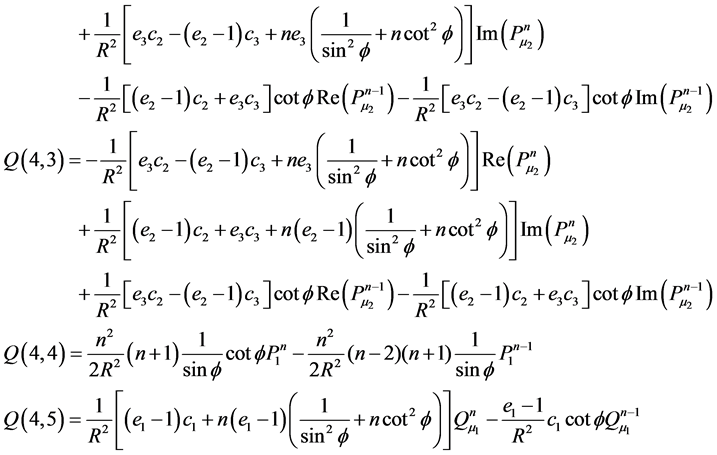
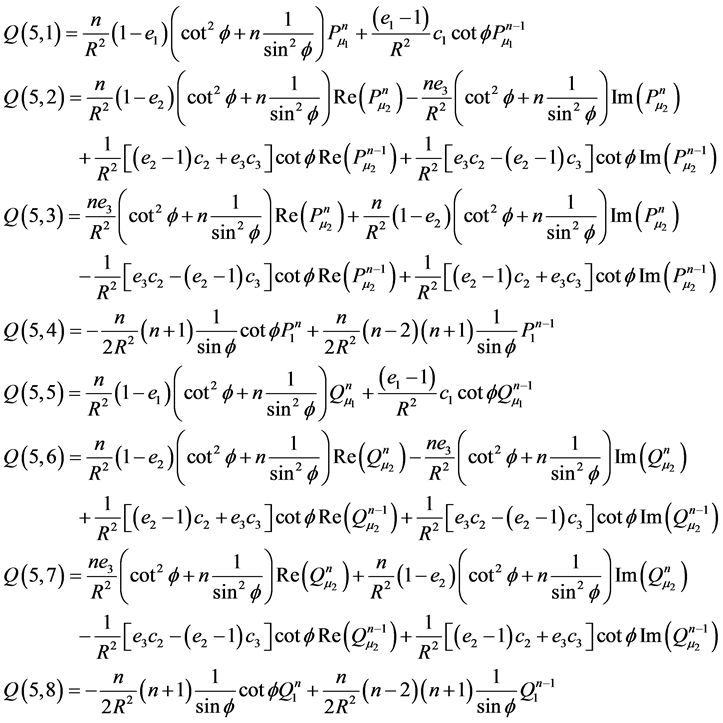
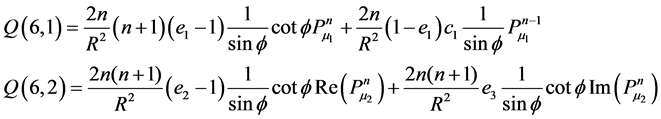
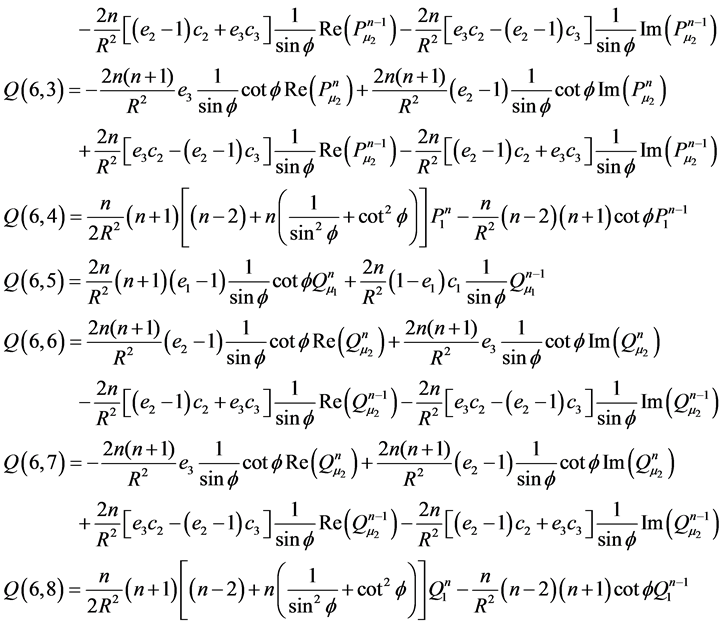
In deriving the above relation we used the recursive relations:



