American Journal of Computational Mathematics
Vol.2 No.2(2012), Article ID:20065,7 pages DOI:10.4236/ajcm.2012.22012
Data Recovering Problem Using a New KMF Algorithm for Annular Domain
LaRIT, Faculty of sciences, Ibn Tofaïl University, Kenitra, Morroco
Email: chakir_tajani@hotmail.fr, abouchabaka3@yahoo.fr, otman.fsk@gmail.com
Received March 16, 2012; revised April 10, 2012; accepted April 18, 2012
Keywords: Inverse Problem; Annular Domain; Laplace Equation; Iterative Method; Freefem
ABSTRACT
This paper is interested at the Cauchy problem for Laplace’s equation, which is to recover both Dirichlet and Neumann conditions on the inaccessible part of the boundary (inner part) of an annular domain from the over specified conditions on the accessible one (outer part). This work is an extension of the proposed algorithm for a unit circle [1] to annular domain, where, we describe an alternating formulation of the KMF algorithm proposed by Kozlov, Mazya and Fomin, and its relationship with the standard formulation. The new KMF algorithm ameliorates the accuracy of the solution and reduces the number of iterations required to achieve convergence. In the last part, the discussion of the error estimation of solution is presented and some numerical tests, using the software Freefem are given to show the efficiency of the proposed method.
1. Introduction
We consider an inverse problem for Laplace equation called data completion problem, which aims at recovering missing conditions on some inaccessible part of the boundary from the over specified boundary data on the remaining part. In this paper, the problem was studied to recover both Neumann and Dirichlet data on the inner part of the boundary of an annular domain, from measurements in the outer part of the domain.
This problem arises and can be encountered as challenge in several areas of engineering, especially in the detection of corrosion problem where the completed data are used to calculate the Robin coefficient that represent the coefficient damage and which is the quotient of these extended data, on the inner boundary [2-4].
This problem is ill-posed in the sense of Hadamard [5], since the existence, uniqueness and stability of the solution are not always assured [6-8]. Solving this problem by direct method is very difficult and leads to unstable solutions in the sense that the solution (if it exists) does not depend continuously on the data.
Many performing numerical methods have been developed to overcome the ill-posed nature of this kind of problem. Among them we mention the method of Quasireversibility introduced by Lattés [9], Thikhonov method [10] and the iterative method [11].
The group of iterative method has the advantage to allow any physical constraint to be easily taken into account directly in the scheme of the iterative algorithm, simplicity of the implementation schemes and the similarity of schemes for problems with linear and non linear operators. One possible disadvantage of this kind of method is the large number of iterations that may be required in order to achieve convergence.
Based on these reasons, we have decided in this work to consider the KMF algorithm addressed by Kozlov, Mazya and Fomin since 1991 [12] (see also [13,14]), also called alternating method since it is to solve alternately two well-posed problems: the first one permits to complete the Dirichlet condition and the second to complete the Neumann condition on the boundary.
To deal with the large number of iterations required to achieve the convergence, we propose in this paper a new KMF algorithm to overcome this problem with more precision. The main idea of the developed algorithm is to divide the boundary of missing data in two parts, and then complete the missing data in alternative way in the two sub-parts of the inaccessible boundary.
This algorithm of data completion problems has been widely studied in the case of simply connected domains, especially on the unit disk [1]. We wish to generalize here this method to annular domains.
The next section is devoted to the presentation of the Cauchy problem for Laplace’s equation for annular domain. In section 3, we present a classical KMF algorithm which enables one to find an approximate solution to that problem; we consider a New KMF algorithm and exhibit the relationship it has with the classical KMF algorithm. Finally, section 4 presents a numerical example showing the feasibility of the alternating formulation, its ability to find an approximate solution more accurately in less iteration.
2. Mathematical Formulation
2.1. Robin Inverse Problem
Let 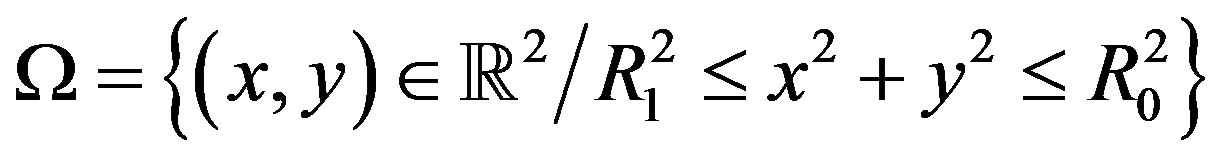 be a doubly connected domain with smooth boundary
be a doubly connected domain with smooth boundary 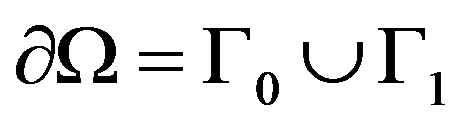 made of two Jordan closed curves
made of two Jordan closed curves  and
and  such that
such that  and
and
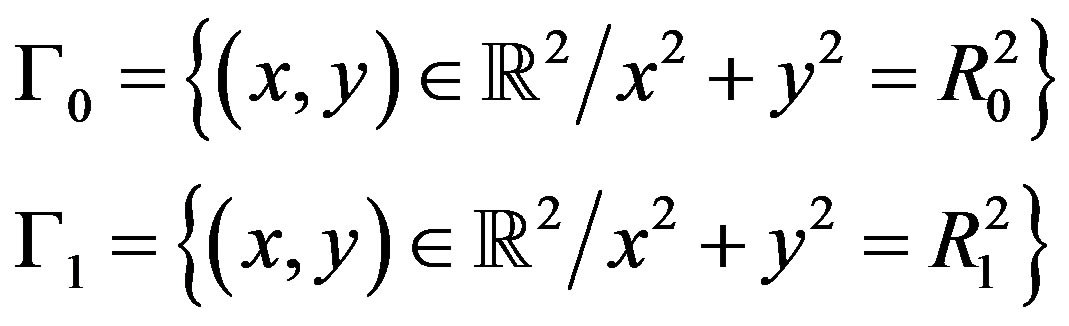

We assume that the corrosion only happened on the interior boundary of the domain  and the corrosion can be described by a non-negative function
and the corrosion can be described by a non-negative function , called coefficient of Robin, in the boundary condition on the interior boundary.
, called coefficient of Robin, in the boundary condition on the interior boundary.
The determination of the coefficient of Robin is an inverse problem that consists to:
Given two functions f and g defined on  or a number of their pointwise measurements, with
or a number of their pointwise measurements, with 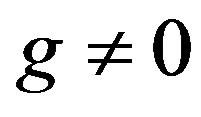 , find a function
, find a function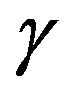 , such that a solution u to:
, such that a solution u to:
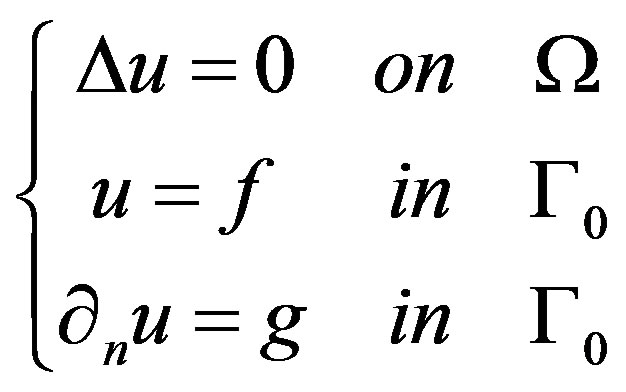 (1)
(1)
also satisfies
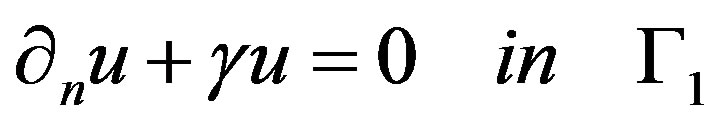 (2)
(2)
where 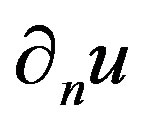 is the normal derivative of u. and
is the normal derivative of u. and 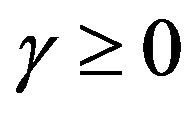 is the coefficient of Robin that represents the corrosion damage.
is the coefficient of Robin that represents the corrosion damage.
In the thermal framework, f corresponds to the measured temperature and g to the imposed heat flux on the outer boundary of a domain, while  is the Robin exchange coefficient to be recovered on the associated inner boundary from the extended data.
is the Robin exchange coefficient to be recovered on the associated inner boundary from the extended data.
This inverse problem consists to find the unknown coefficient 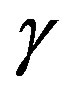 from the Cauchy data f and g on
from the Cauchy data f and g on 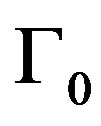 . That can be treated by the following steps:
. That can be treated by the following steps:
Step 1: Get the Cauchy data on the interior circle by solving the Cauchy problem for Laplace’s equations (1).
Step 2: Get the impedance 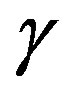 from the Cauchy data on the interior circle.
from the Cauchy data on the interior circle.
From the boundary condition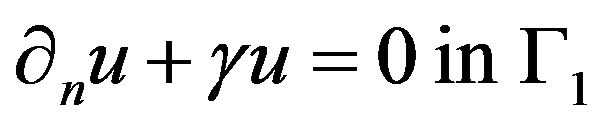 ,
, 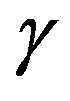
can be obtained by 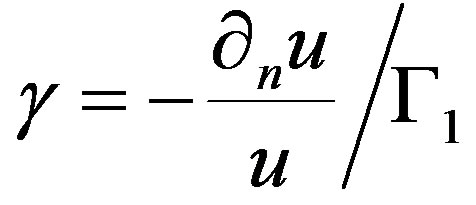 if
if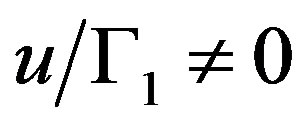 .
.
2.2. Reconstruction Problem
In this paper, we consider the problem of the step 1 to complete the missing data which consist to recover both Dirichlet and Newman conditions in the inner part of the annular domain.
This problem has a unique solution for compatible data f and g which means that the over specified data is indeed the trace and normal derivative of the solution of a single harmonic function. i.e.
For 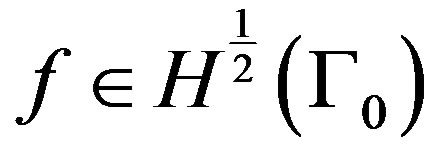 and
and , where
, where
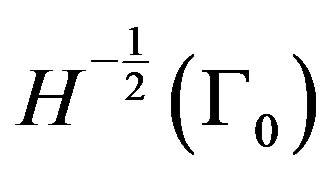 is defined as dual space of
is defined as dual space of 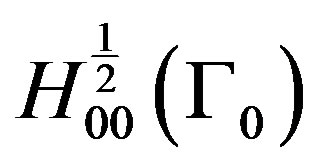 and
and

the problem (1) has a unique solution.
3. Description of the Algorithm
3.1. KMF Standard Algorithm
Consider the Cauchy problem (1) with 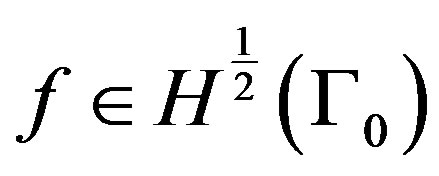 and
and . The iterative algorithm proposed by Kozlov, Mazya and Fomin (KMF standard Algorithm) [12] investigated is based on reducing this ill-posed problem to a sequence of mixed well-posed boundary value problems and consists of the following steps:
. The iterative algorithm proposed by Kozlov, Mazya and Fomin (KMF standard Algorithm) [12] investigated is based on reducing this ill-posed problem to a sequence of mixed well-posed boundary value problems and consists of the following steps:
Step 1. Specify an initial guess 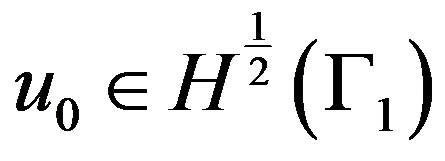
Step 2. Solve the following mixed well-posed boundary value problem:
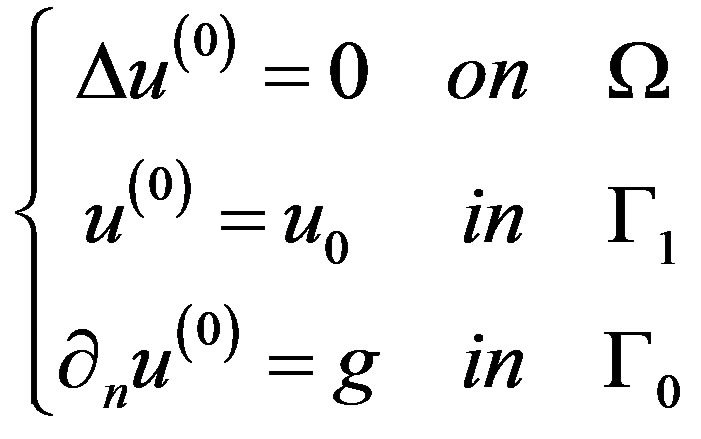 (3)
(3)
To obtain
 (4)
(4)
Step 3. For , solve alternatively the two mixed well-posed boundary value problems:
, solve alternatively the two mixed well-posed boundary value problems:
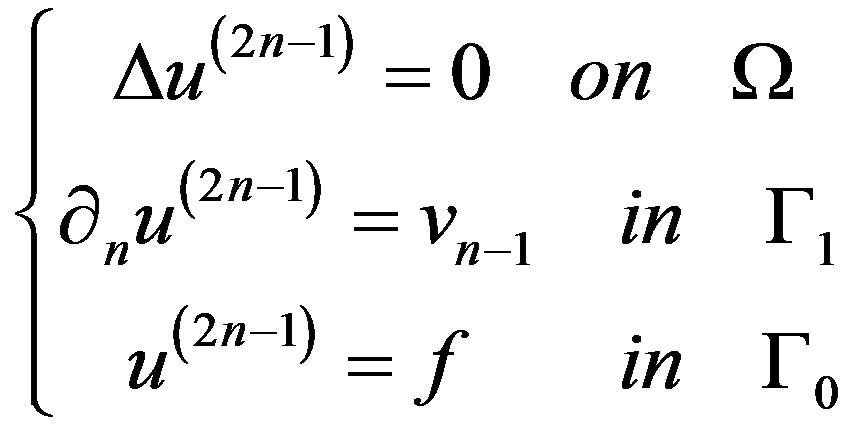 (5)
(5)
To obtain
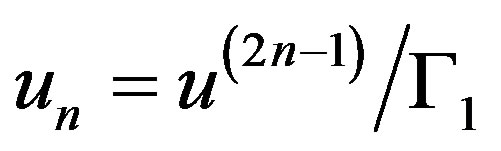 (6)
(6)
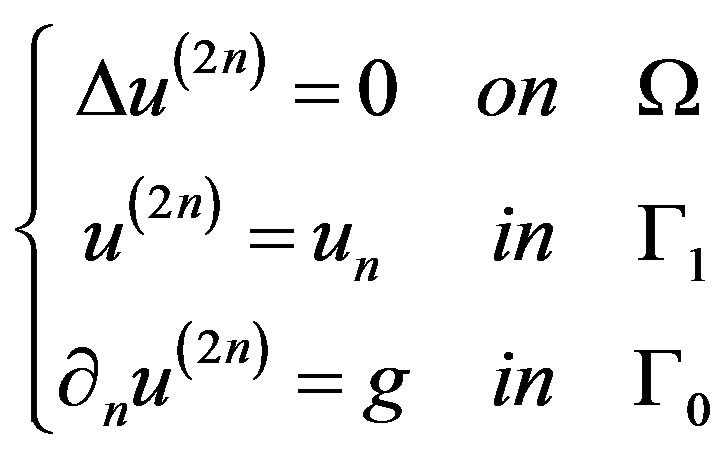 (7)
(7)
To obtain
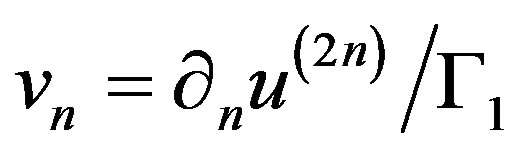 (8)
(8)
Step 4. Repeat step 3 from 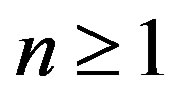 until a prescribed stopping criterion is satisfied.
until a prescribed stopping criterion is satisfied.
Ÿ 3.2. Observation
Ÿ If the sequence 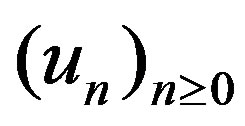 defined in Equation (6) converges in
defined in Equation (6) converges in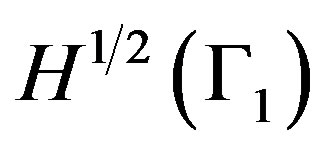 , then the sequence
, then the sequence 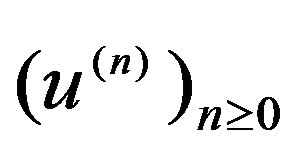 converges in
converges in 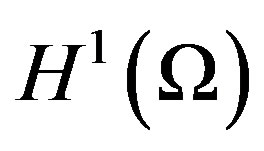 to the solution
to the solution  of the Cauchy problem (1).
of the Cauchy problem (1).
Ÿ The same conclusion is obtained if at the step 1, we specify an initial guess 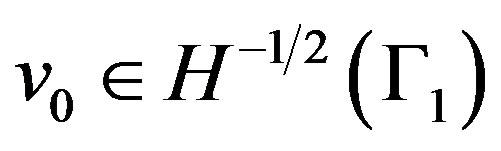 instead of an initial guess for
instead of an initial guess for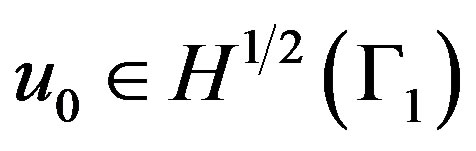 , and we modify accordingly the steps 2 and 3 of the algorithm.
, and we modify accordingly the steps 2 and 3 of the algorithm.
Ÿ This algorithm provides an approximate solution to exact solution in a large number of iterations
Ÿ In order to accelerate the convergence of the iterative algorithm, schemes have been developed [15] by introducing a relaxation parameter in the Neumann condition obtained after the third step and replacing (8) by:
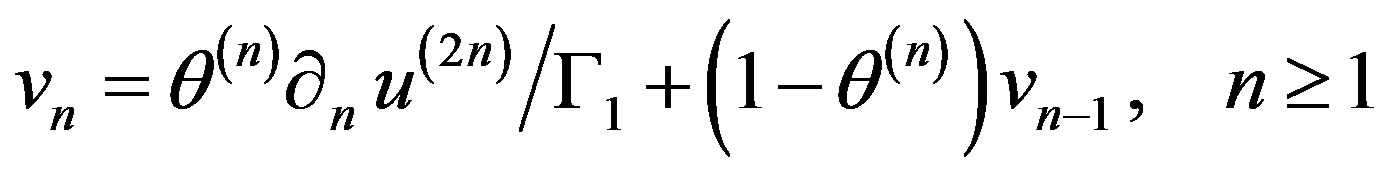 (9)
(9)
where  is a positive relaxation factor Or in the Dirichlet condition obtained after the third step and replacing (6) by:
is a positive relaxation factor Or in the Dirichlet condition obtained after the third step and replacing (6) by:
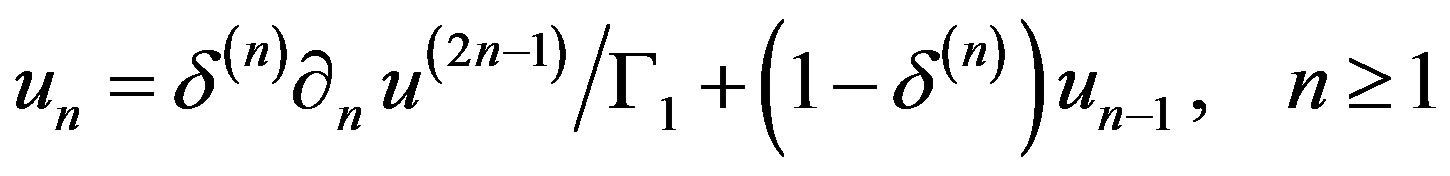 (10)
(10)
where 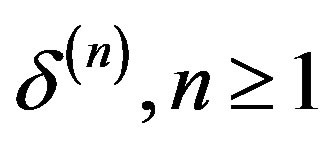 is a positive relaxation factor.
is a positive relaxation factor.
Or in both Dirichlet and Neumann conditions obtained after the third step and replacing (6) and (8) by:
 (11)
(11)
where  are two positives relaxation factor.
are two positives relaxation factor.
3.3. New KMF Algorithm
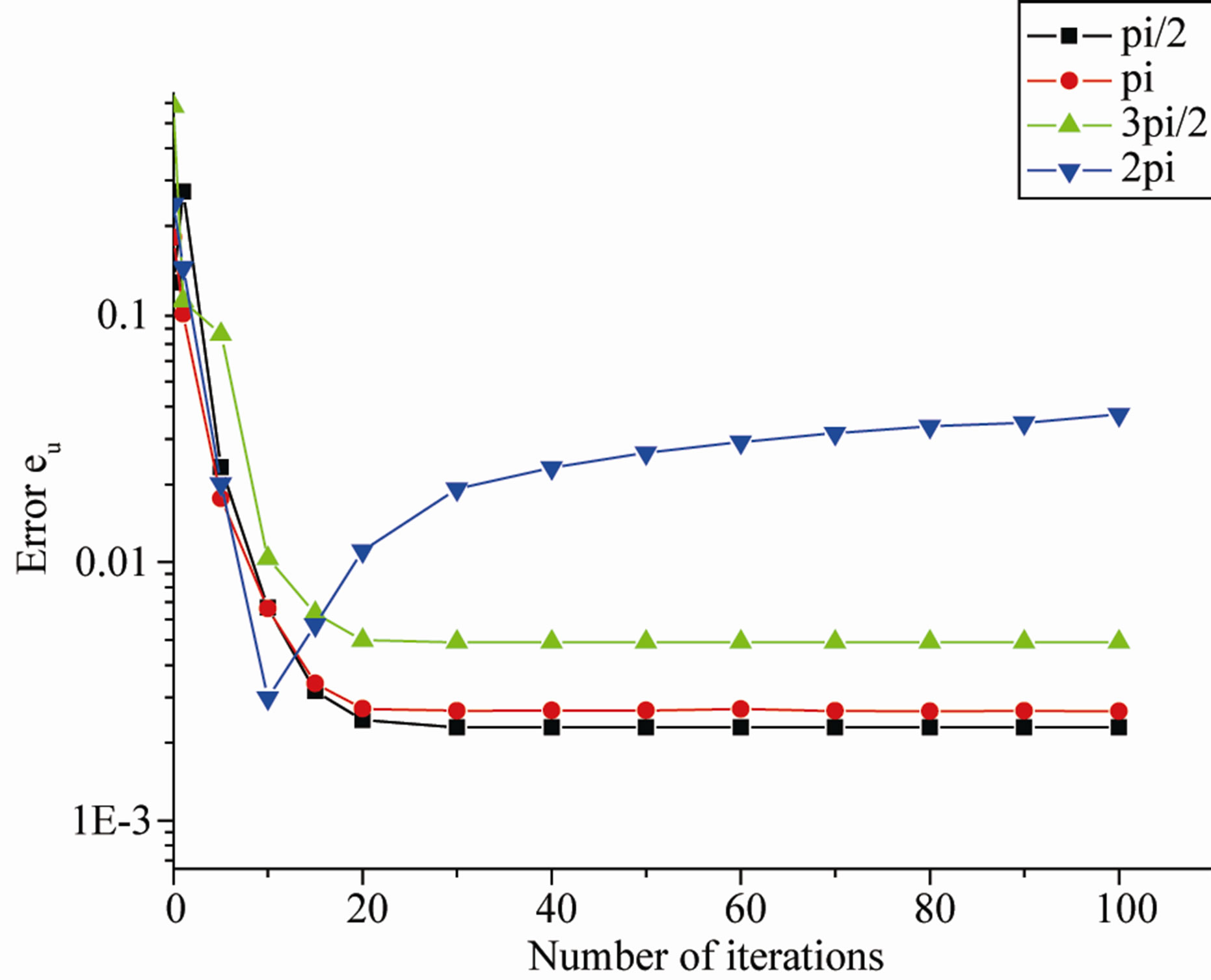
As first work [16], we are studied the influence of data problems, particularly; the relationship between the measure of the inaccessible part of the boundary and the rate of convergence has shown that:
Ÿ The convergence is always guaranteed and it is very fast if the measure of the part of the boundary to be completed is small (Figure 1).
Ÿ The convergence requires much more iterations if the inaccessible part is greater.
In this study we extend to the annular domain, the New KMF algorithm in order to improve the rate of convergence of the iterative algorithm described.
The main idea of the proposed algorithm proposed is based on the use of the previous results and the KMF standard algorithm by completing the missing data in alternative way to the two sub-parts of the inaccessible boundary. The inaccessible part is subdivided in two parts, and the KMF standard algorithm is used to complete the data in the first part, then to complete the data in the second part in an alternative way.
For this, we consider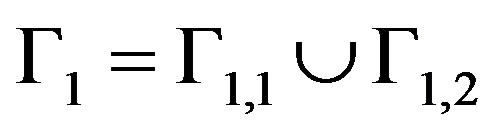 such that
such that
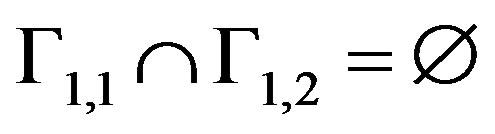 and
and 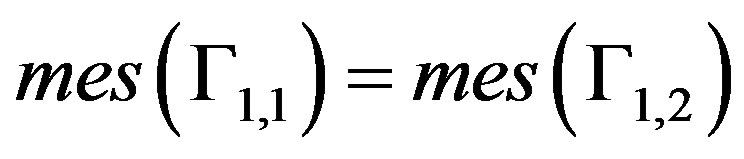
 (a)
(a)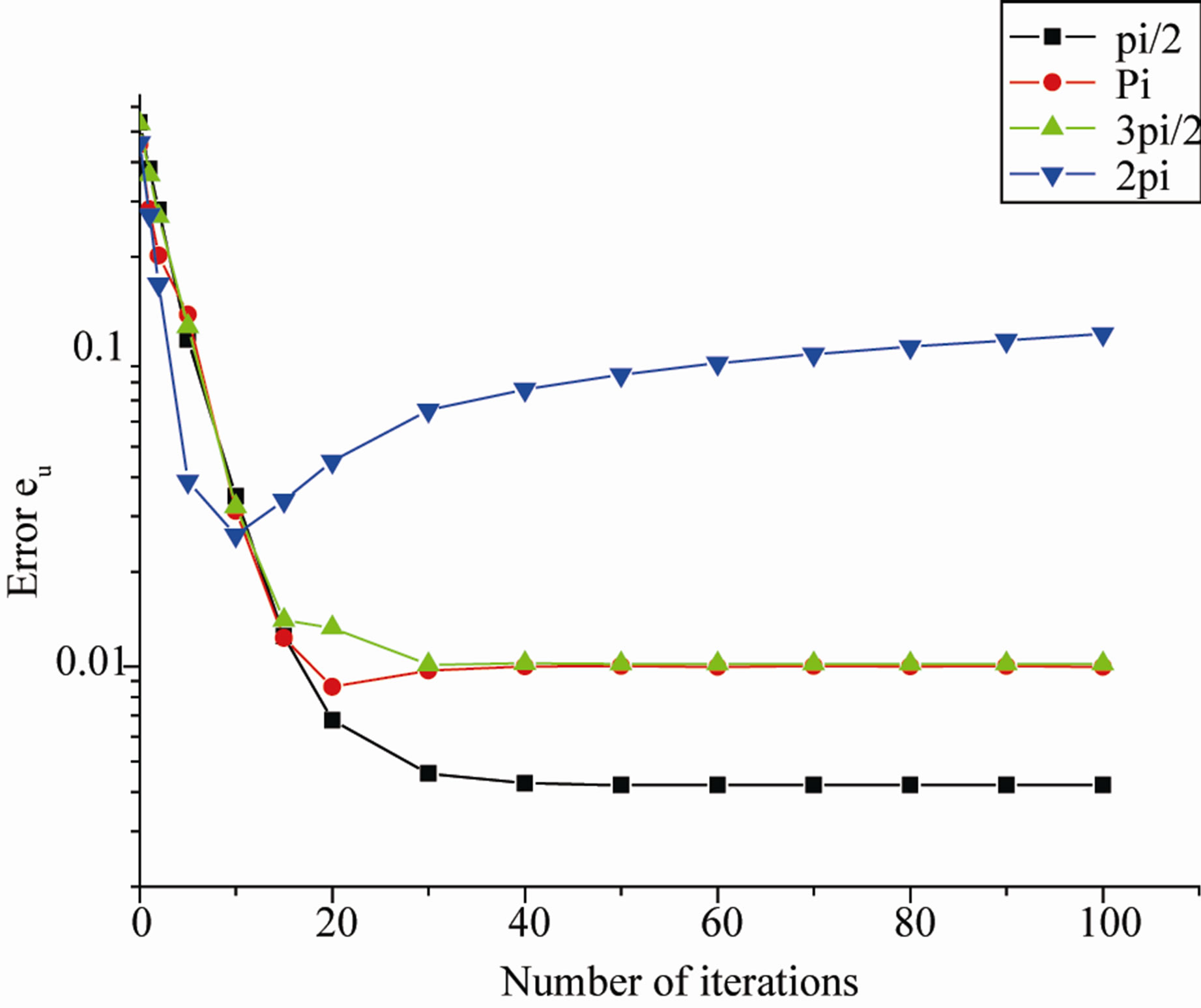 (b)
(b)
Figure 1. The numerical results obtained for eu (a) and ev (b) for different choice of θ.
The algorithm consists of the following steps:
Step 1. Specify an initial guess 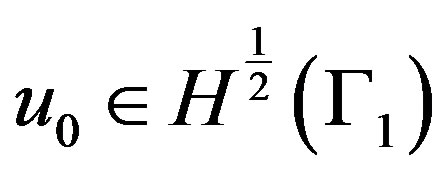
Step 2. Solve the well-posed problem
 (12)
(12)
To obtain

and
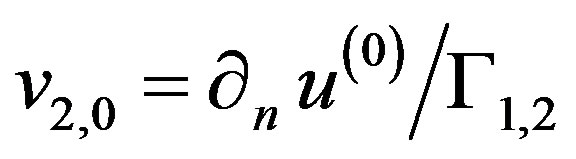 (13)
(13)
Step 3. For 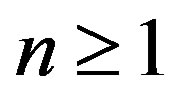 solve the two well-posed problems
solve the two well-posed problems
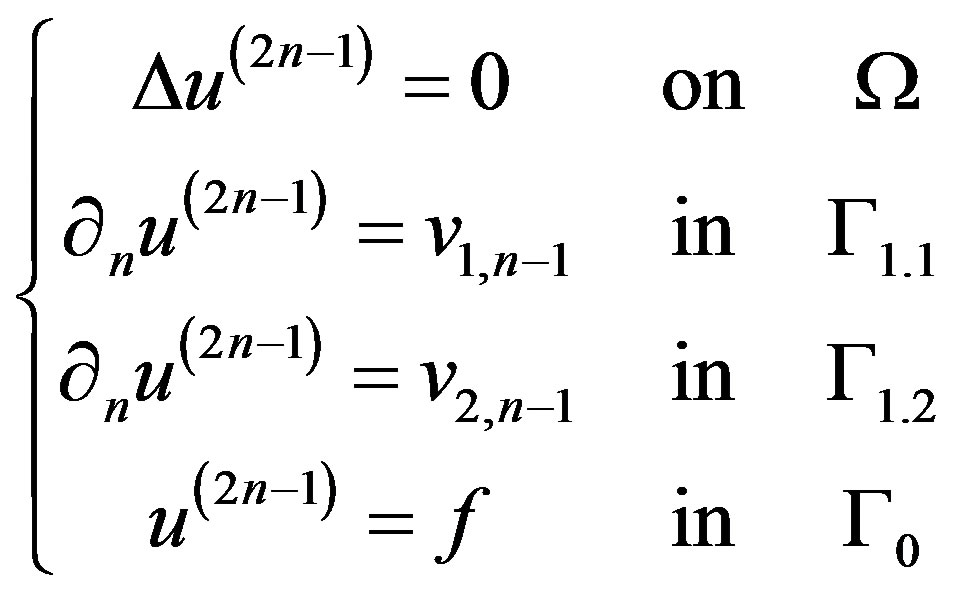 (14)
(14)
To obtain
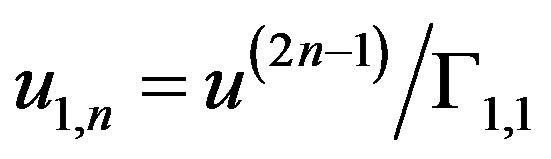 (15)
(15)
and
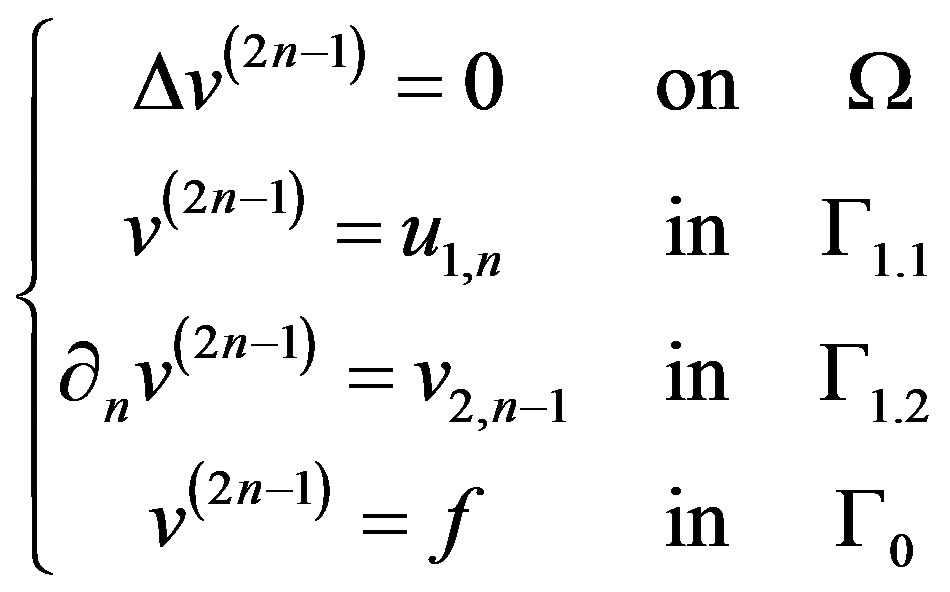 (16)
(16)
To obtain
 (17)
(17)
Step 4. Solve the two well-posed problems
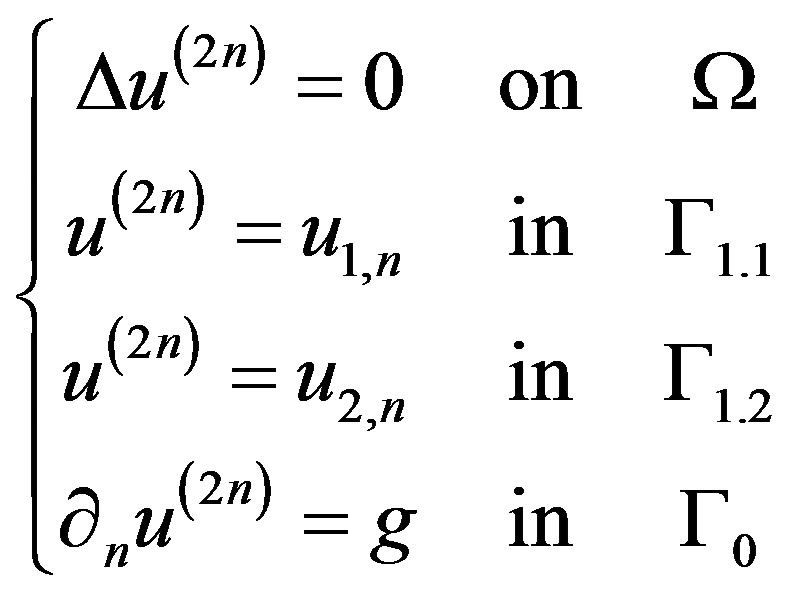 (18)
(18)
To obtain
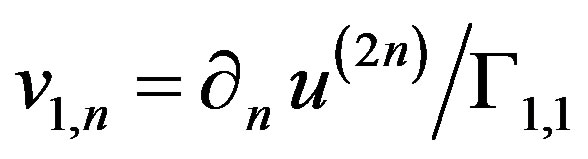 (19)
(19)
And
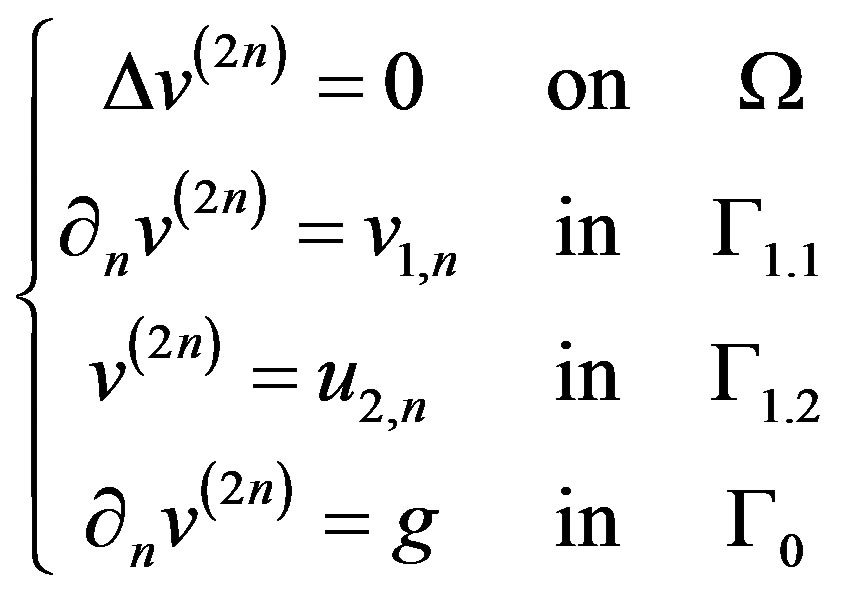 (20)
(20)
To obtain
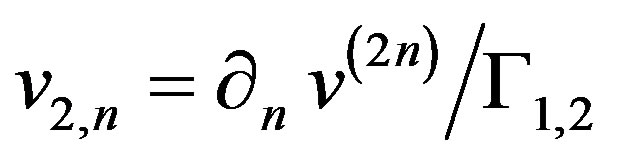 (21)
(21)
Step 5. Repeat steps 3 and 4. From  until a prescribed stopping criterion is satisfied.
until a prescribed stopping criterion is satisfied.
Ÿ 3.4. Remarks
Ÿ If we consider every iteration to consist of solving the four mixed well-posed problems from the Step 3 and 4 of the algorithm, then for every 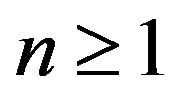 the following approximations are obtained at the iteration number n:
the following approximations are obtained at the iteration number n:
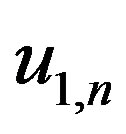 for the Dirichlet condition on the
for the Dirichlet condition on the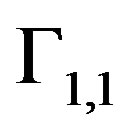 .
.
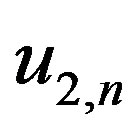 for the Dirichlet condition on the
for the Dirichlet condition on the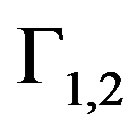 .
.
 for the Neumann condition on the boundary
for the Neumann condition on the boundary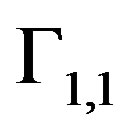 .
.
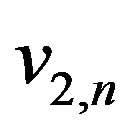 for the Neumann condition on the boundary
for the Neumann condition on the boundary .
.
It should be noted that:
Ÿ The KMF developed algorithm can be seen as two parallel problems of KMF standard algorithm. These two problems are initialized with the same initial data. Each problem allows to obtain approximation in each subpart  (for the approximation in
(for the approximation in 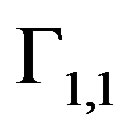 the two well-posed problems (14) and (18), for the approximation in
the two well-posed problems (14) and (18), for the approximation in 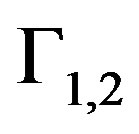 the two well-posed problems (16) and (20).
the two well-posed problems (16) and (20).
Ÿ Each solved problem allows an approximation in one of the inaccessible subparts that can be introduced in the other well-posed problems.
Ÿ The missing Dirichlet condition in the part 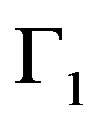 can be obtained from the problem (16) since the condition
can be obtained from the problem (16) since the condition 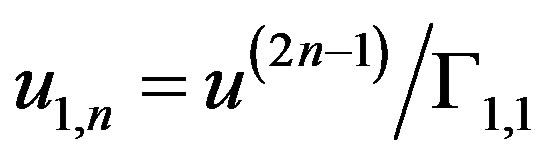 obtained from (14) is introduced in (16) which also provides
obtained from (14) is introduced in (16) which also provides 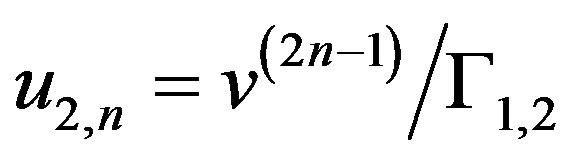 .
.
Ÿ The missing Neumann condition in the part  can be obtained from the problem (20), since the condition
can be obtained from the problem (20), since the condition 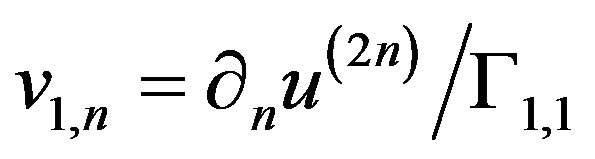 obtained from (18) is introduced in (20) which also provides
obtained from (18) is introduced in (20) which also provides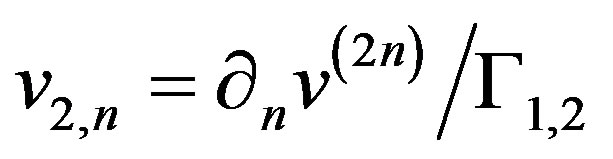 .
.
4. Numerical Results
In order to present the performance of the numerical method proposed, we solve the Cauchy problem for Laplace equation for annular domain with R1 = 0.5 and R0 = 1.
In this section, we illustrate the numerical results obtained using the alternating KMF algorithm described in section 3. In addition, we investigate the convergence and the accuracy of the solution with respect the number of iterations.
We assume that the boundary 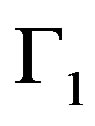 of the solution domain is divided into two disjointed parts
of the solution domain is divided into two disjointed parts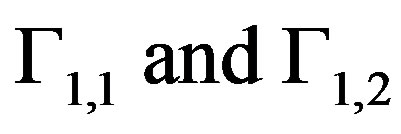 , namely;
, namely;
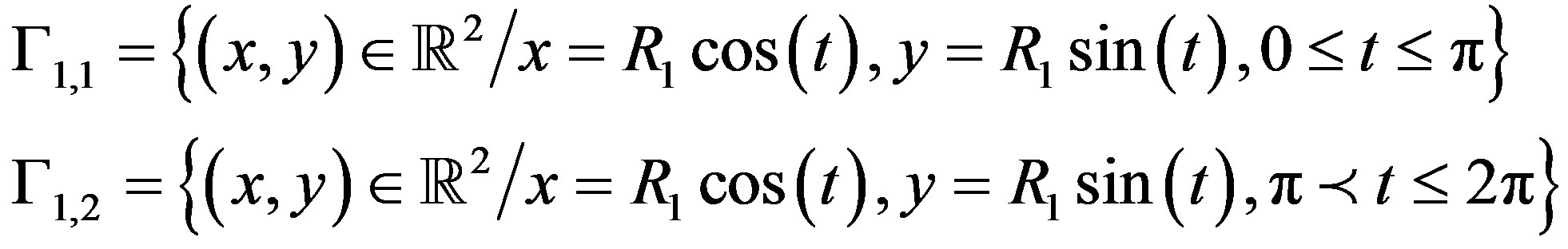
The analytical function to be retrieved is given by:
 (22)
(22)
For the implementation of the iterative algorithm we use the software FreeFem, and solve the well-posed problems in the algorithm by the finite element method. In this example, we use a finite element method with continuous piecewise linear polynomials to provide simultaneously the unspecified boundaries Dirichlet and Neumann.
The following stopping criterion was adopted
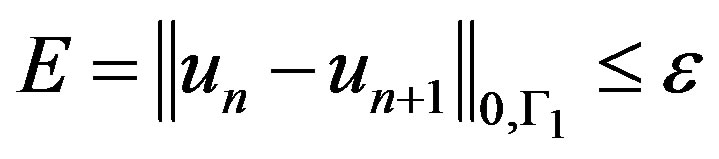 (23)
(23)
where 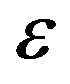 is a small positive number.
is a small positive number.
The convergence of the algorithm may be investigated by evaluating at every iteration the error:
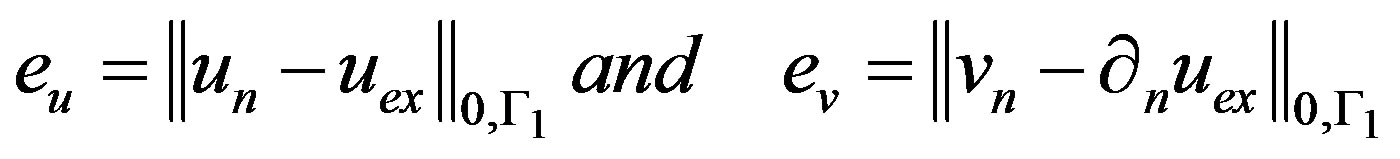 (24)
(24)
where the approximation 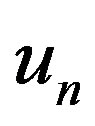 is obtained for the function on the boundary
is obtained for the function on the boundary 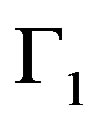 after n iterations and
after n iterations and 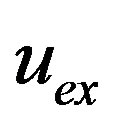 is the exact solution of the problem of the problem (1). However, in practical applications the error
is the exact solution of the problem of the problem (1). However, in practical applications the error 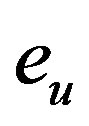 cannot be evaluated since the analytical solution is not known and therefore the error E has to be used.
cannot be evaluated since the analytical solution is not known and therefore the error E has to be used.
The Figure 2 presents the function u obtained after convergence (u_iter final), the function u with the initial guess considered (u_iter 0) and the exact solution (u_exact). You can see that; from a given initial data not very close to exact solution, we obtained a very satisfactory approximation of the solution of problems in an acceptable number of iterations.
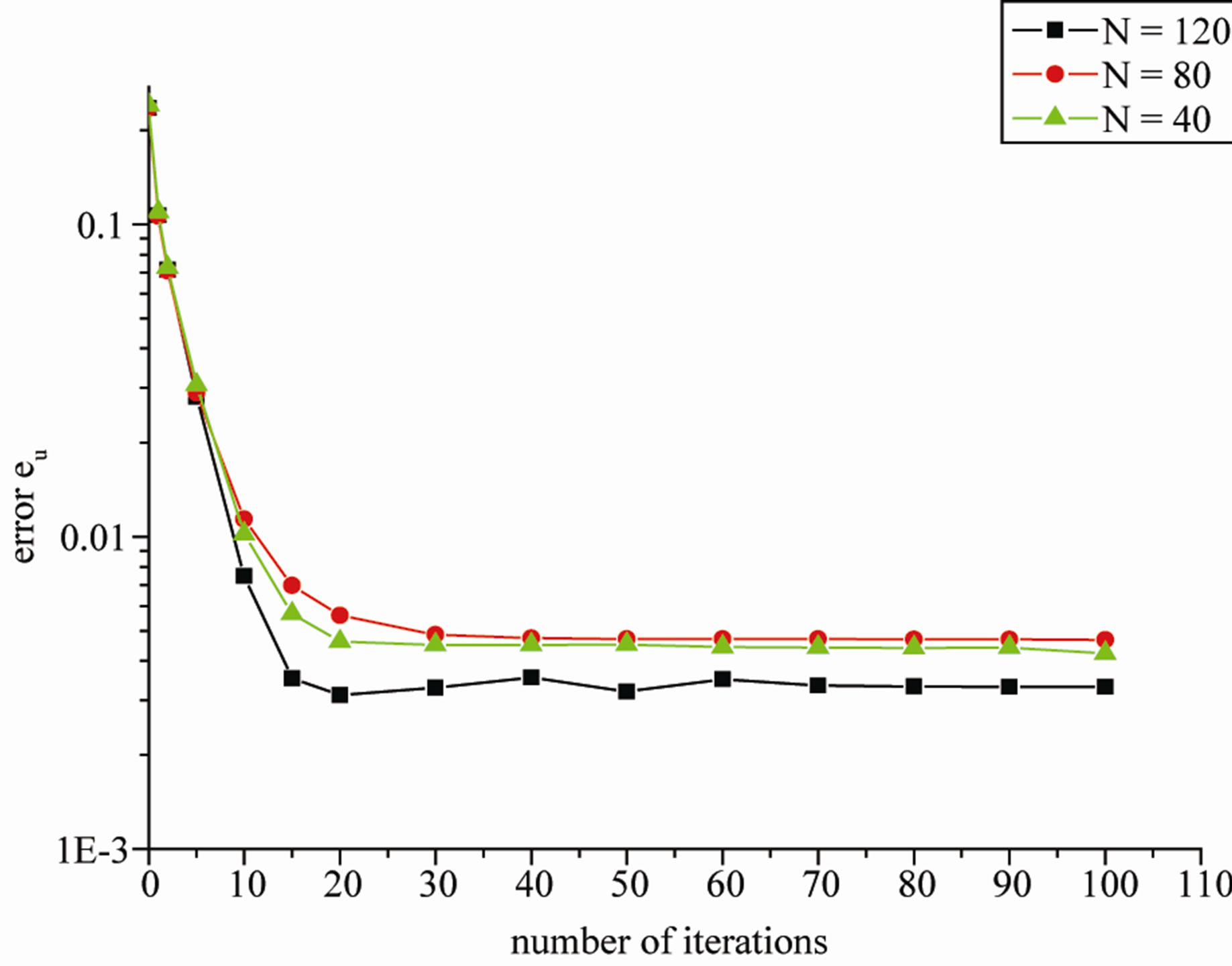
Figure 3 presents the error 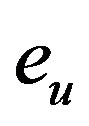 and
and 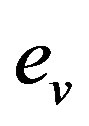 obtained for different number of boundary elements used for discretising the inner part of the boundary
obtained for different number of boundary elements used for discretising the inner part of the boundary .
.
Figure 4 presents a comparison between the numerical results 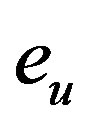 and
and 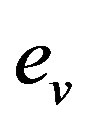 obtained with the KMF standard algorithm and the New KMF algorithm. It can be seen that the algorithm proposed decreases considerably the number of iteration necessary to achieve the convergence that can be reduced, and present a more accurate approximations for both Dirichlet and Neumann missing data. In addition, we can notice that after the number of iterations is sufficiently increased, the error become small for the new algorithm; this shows that the numerical solution is accurate and consistent with the number of iterations.
obtained with the KMF standard algorithm and the New KMF algorithm. It can be seen that the algorithm proposed decreases considerably the number of iteration necessary to achieve the convergence that can be reduced, and present a more accurate approximations for both Dirichlet and Neumann missing data. In addition, we can notice that after the number of iterations is sufficiently increased, the error become small for the new algorithm; this shows that the numerical solution is accurate and consistent with the number of iterations.
Figure 5 shows the numerical results obtained in approximating the function u in the part of the boundary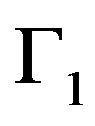 , indicating that from a choice of an initial data, we obtain satisfying results for both algorithms (stand and New). However, the New KMF algorithm requires less iteration to achieve more accurate convergence.
, indicating that from a choice of an initial data, we obtain satisfying results for both algorithms (stand and New). However, the New KMF algorithm requires less iteration to achieve more accurate convergence.
5. Conclusions
In this paper, we have presented a fast data completion algorithm solving the Cauchy problem for the Laplace
 u_iter 0
u_iter 0 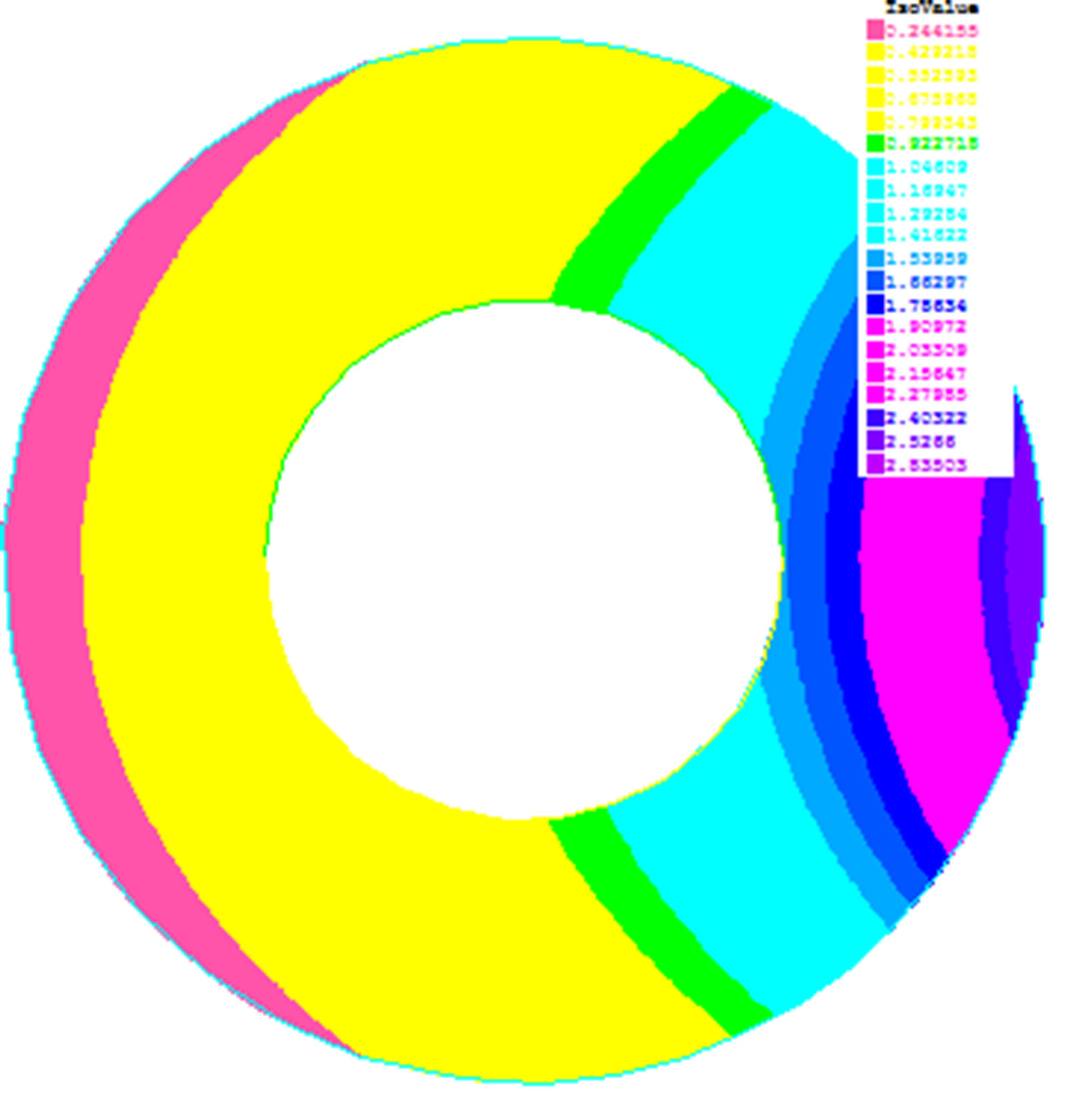 u_iter final
u_iter final 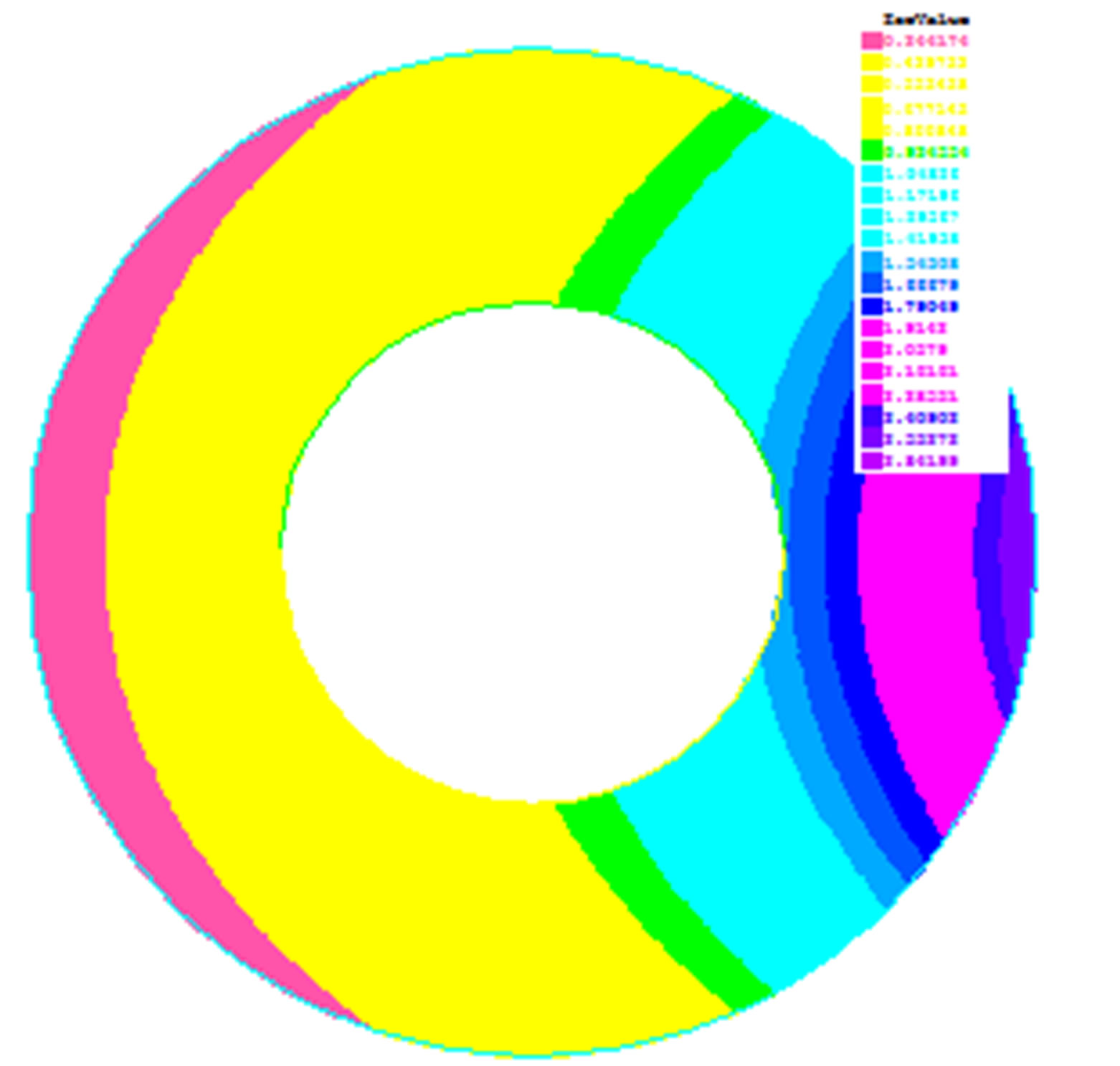 u_exact
u_exact
Figure 2. The reconstruction function u with the new algorithm (u_iter final) in comparison with (u_exact) and u obtained with the initian guess (u_iter 0) for R1 = 0.5 and R0 = 1 and N0 = N1 = 40.
 (a)
(a)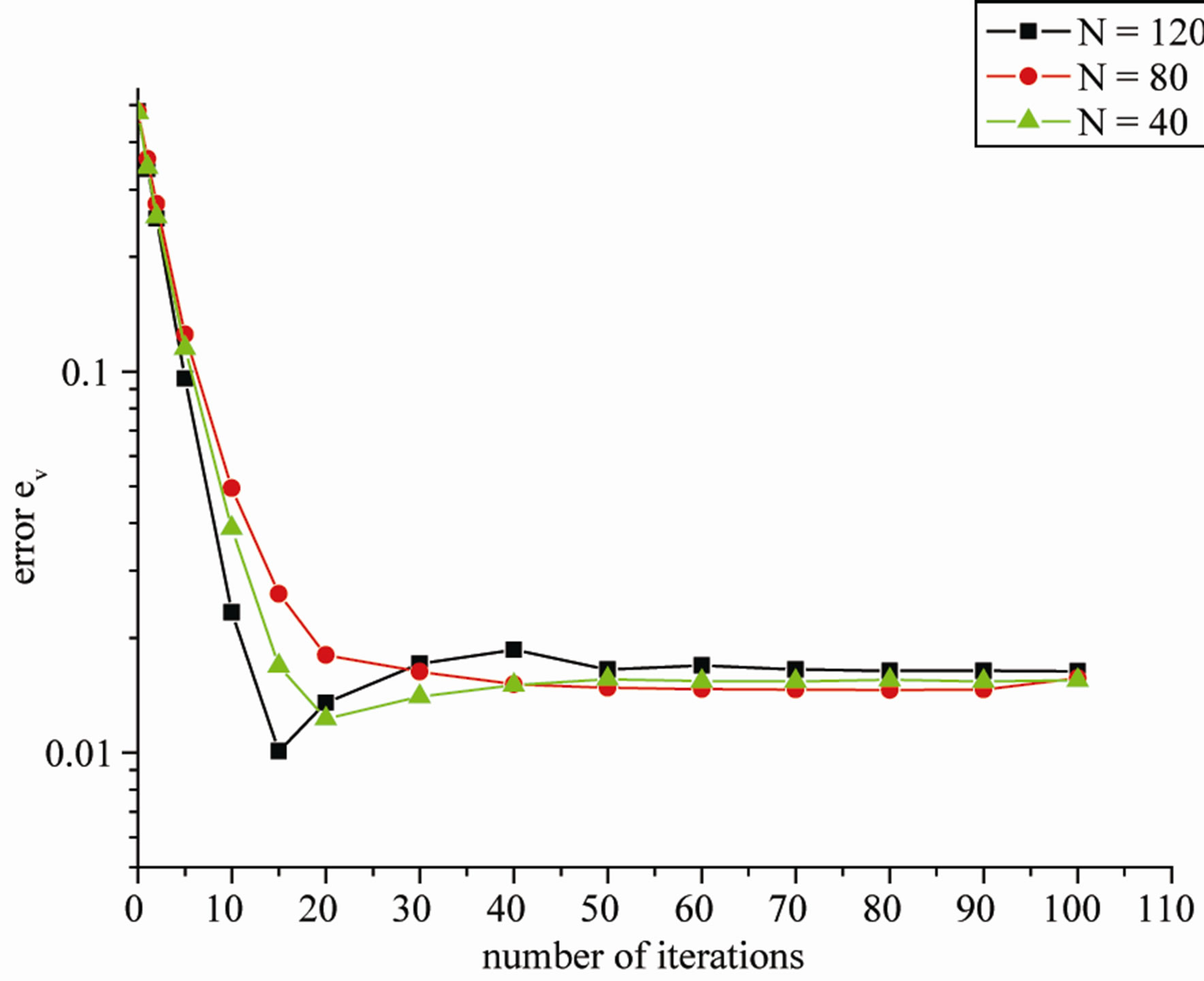 (b)
(b)
Figure 3. The error eu and ev as a function of the number of iterations obtained for KMF developed algorithm with N = 40, 80, 120.


Figure 4. The error eu and ev as a function of the number of iterations obtained for KMF developed algorithm (New) in comparison with classical algorithm (Stand).
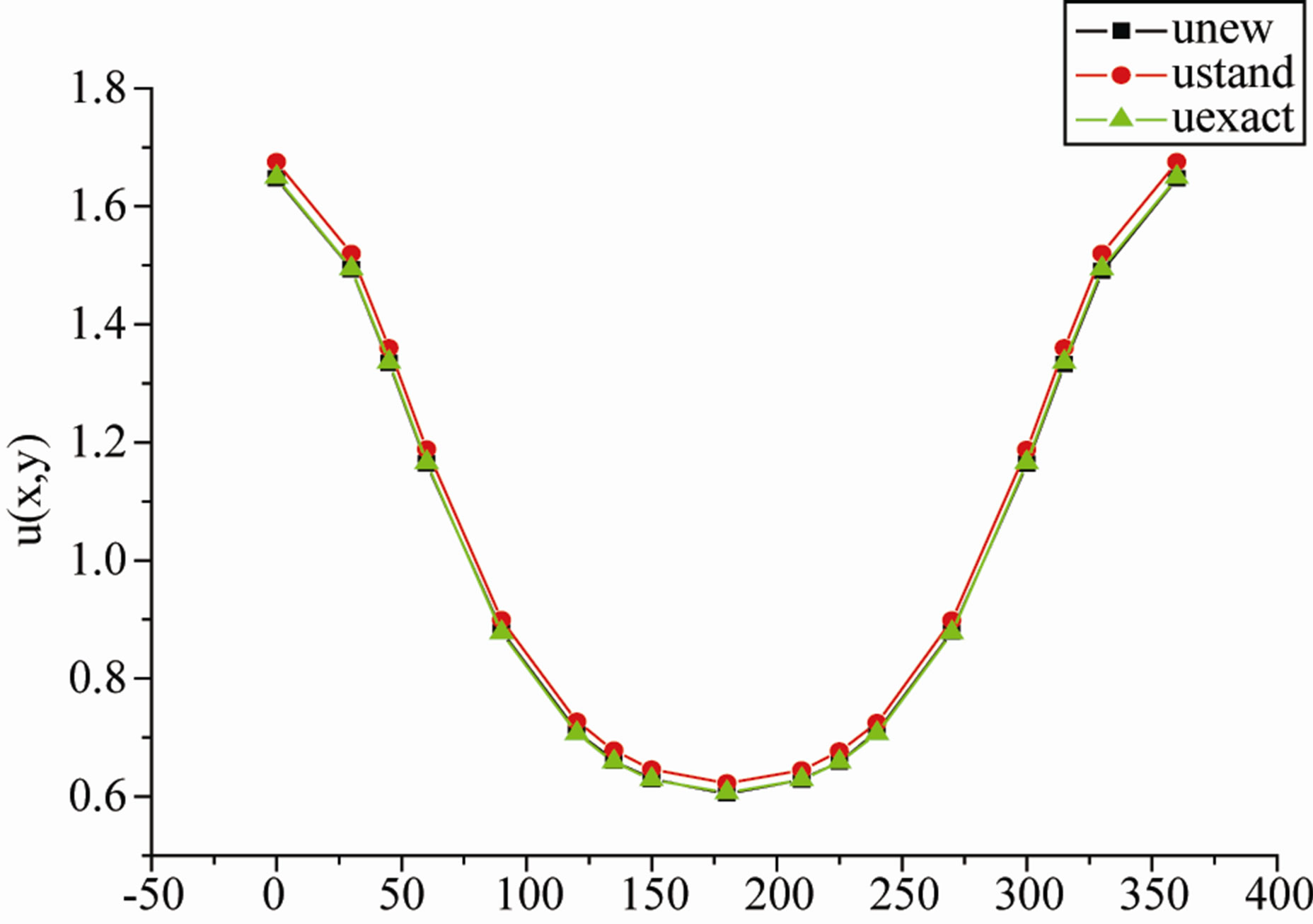
Figure 5. The numerical results for the function u on the boundary Γ1 obtained with KMF developed algorithm (unew) in comparison with the analytical solution (uexact) and the solution with KMF standard algorithm (ustand).
equation in an annular domain. The main goal was to compute accurately the extended data on the inaccessible inner part from the over specified data in the accessible outer part. These data can be used to calculate the coefficient data representing the corrosion damage on the inner part of the boundary.
The comparison of numerical results with those obtained by the KMF standard algorithm show that the proposed algorithm significantly reduces the number of iterations needed to achieve the convergence and produces more accurate results. In addition, it can be concluded that the proposed algorithm is very efficient to reduce the rate of convergence. When perturbations are introduced into the given date problem the results are stable. Overall, it can be concluded that the new iterative algorithm proposed produces a convergent, stable and accurate numerical solution.
REFERENCES
- C. Tajani and J. Abouchabaka, “An alternating KMF algorithm to solve the Cauchy problem for Laplace’s equation,” International Journal of Computer Applications, Vol. 38, No. 8, 2012, pp. 30-36.
- X. Yang, M. Choulli and J. Cheng, “An iterative BEM for the Inverse Problem of Detecting Corrosion in a pipe,” Numerical Mathematics: A Journal of Chinese Universities, Vol. 14, No. 3, 2005, pp. 252-266.
- J. Leblond, M. Mahjoub and J. R. Partington, “Analytic extensions and Cauchy-type Inverse Problems on annular Domains: Stability Results,” Journal of Inverse and III-posed Problems, Vol. 14, No. 2, 2006, pp. 189-204. doi:10.1515/156939406777571049
- M. Jaoua, J. Leblond and M. Mahjoub, “Robust Numerical Algorithms Based on Analytic Approximation for the solution of Inverse Problems in Annular Domains,” IMA Journal of Applied Mathematics, Vol. 74, No. 4, 2009, pp. 481-506.
- J. Hadamard, “Lectures on the Cauchy Problem in Linear Partial Differential Equations,” Yale University Press, New Haven, 1923.
- V. Isakov, “Inverse Problems for Partial Differential Equations, Applied Mathematical Sciences,” Springer, New York, 1998.
- L. E. Payne, “Improperly Posed Problems in Partial Differential Equations,” SIAM, Philadelphia, 1975.
- M. M. Lavrentiev, “Some improperly Posed Problems of Mathematical,” Springer-Verlag, Berlin, 1967.
- R. Lattes and J. L. Lions, “Mèthode de Quasi-reversibilité et Applications, ” Dunod, Paris, 1967.
- A. Cimetière, F. Delvare, M. Jaoua and F. Pons, “Solution of the Cauchy Problem Using Iterated Tikhonov regularization,” Inverse Problems, Vol. 17, No. 3, 2001, pp. 553-570. doi:10.1088/0266-5611/17/3/313
- D. Lesnic, L. Elliott and D. B. Ingham, “An Iterative Boundary Element Method for Solving Numerically the Cauchy problem for the Laplace equation,” Engineering Analysis with Boundary Elements, Vol. 20, No. 2, 1997, pp. 123-133. doi:10.1016/S0955-7997(97)00056-8
- V. A. Kozlov, V. G. Maz’ya and D. V. Fomin, “An Iterative Method for solving the Cauchy problem for Elliptic Equation,” Computational Mathematics and Mathematical Physics, Vol. 31, No. 1, 1991, pp. 45-52.
- M. jourhmane and A. Nachaoui, “An Alternating Method for an inverse Cauchy problem,” Numerical Algorithms, Vol. 21, No. 1-4, 1999, pp. 247-260. doi:10.1023/A:1019134102565
- C. Tajani and J. Abouchabaka, “Missing Boundary Data Reconstruction by an Alternating Iterative Method,” International Journal of Advances in Engineering and Technology, Vol. 2, No. 1, 2012, pp. 578-586.
- M. Jourhmane, D. Lesnic and N. S. Mera, “Relaxation procedures for an Iterative Algorithm for solving the Cauchy problem for the Laplace equation,” Engineering Analysis with Boundary Elements, Vol. 28, No. 6, 2004, pp. 655-665. doi:10.1016/j.enganabound.2003.07.002
- C. Tajani, J. Abouchabaka and O. Abdoun, “Numerical simulation of an Inverse Problem: Testing the influence data,” proceedings of the 4th International Conference on Approximation Methods and Numerical Modeling in Environment and Natural, Saidia, 23-26 May 2011, pp. 29-32.

