American Journal of Computational Mathematics
Vol.3 No.2(2013), Article ID:33539,4 pages DOI:10.4236/ajcm.2013.32018
New Improved Variational Homotopy Perturbation Method for Bratu-Type Problems
Department of Industrial Mathematics, Landmark University, Omu Aran, Nigeria
Email: sola4one@yahoo.com
Copyright © 2013 Olusola Ezekiel Abolarin. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received January 31, 2013; revised March 1, 2013; accepted March 29, 2013
Keywords: Bratu-Type Problem; Variational Iteration Method; Homotopy Perturbation Method; New Improved Variational Homotopy Perturbation Method; Boundary Value Problems; Initial Value Problems
ABSTRACT
This research paper deals with the boundary and initial value problems for the Bratu-type model by using the New Improved Variational Homotopy Perturbation Method. The New Method does not require discritization, linearization or any restrictive assumption of any form in providing analytical or approximate solutions to linear and nonlinear equation without the integral related with nonlinear term. Theses virtues make it to be reliable and its efficiency is demonstrated with numerical examples.
1. Introduction
The Bratu-type boundary value problem in one-dimensional planar coordinates
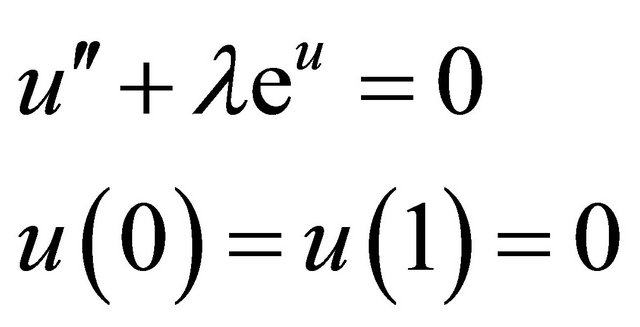 (1.1)
(1.1)
arises from a simplification of the solid fuel ignition model in thermal combustion theory, physical applications ranging from chemical reaction theory, radiative heat transfer and nanotechnology to the expansion of universe [1-5]. The initial value problem of the Bratutype model [5] is given by
 (1.2)
(1.2)
Due to its mathematical and physical properties, the Bratu-type problems have been studied extensively [4-8]. Recently, Wazwaz [5] applied Adomian decomposition method to study the Bratu-type equations, Syam [4] discussed the Bratu-type problems with variational iteration method, and Feng [6] considered these problems by means of modified homotopy perturbation method. However, the existing methods such as Adomian decomposition method, variational iteration method and homotopy perturbation method involve the computation of Adomian polynomials, and the integral related with eu or the perturbation of small parameters, this leads to increase the numerical computation cost and narrow down their applications. To avoid these disadvantages, Lin Jin [9] proposed a modified variational iteration method to solve the Bratu problems, based upon the Taylor series expansion. In order to improve on what Lin Jin [9] has done, we introduce the New Improved Variational Homotopy Perturbation Method for Bratu-Type Problems which is a time cost effective and uses friendly.
2. Variational Iteration Method and Its Modification
To illustrate the basic concepts of the variational iteration method [10-12], we consider the following differential equation:
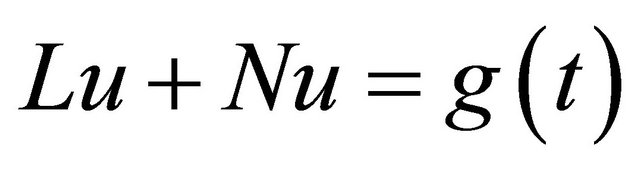 (2.1)
(2.1)
where L is a linear operator, N is a nonlinear operator, and 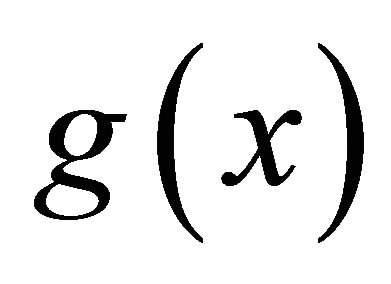 is an inhomogeneous term. Then, we can construct a correct functional as follows:
is an inhomogeneous term. Then, we can construct a correct functional as follows:
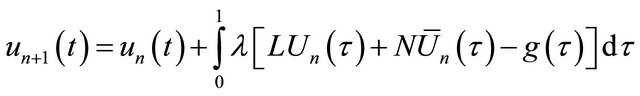 (2.2)
(2.2)
where 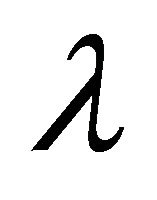 is a general Lagrange multiplier [10,11], which can be optimally identified via variational theory. The second term on the right is called the correction and
is a general Lagrange multiplier [10,11], which can be optimally identified via variational theory. The second term on the right is called the correction and 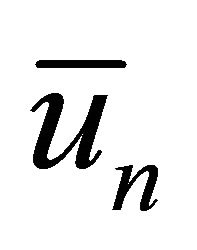 is considered as a restricted variation, i.e.
is considered as a restricted variation, i.e.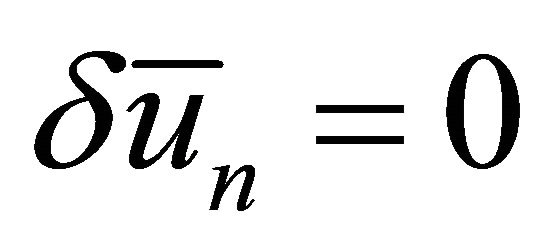 . For the nonlinear differential Equation (2.1), the nonlinear term
. For the nonlinear differential Equation (2.1), the nonlinear term  can be expressed in Taylor series
can be expressed in Taylor series

We determine the Lagrange multiplier  in the correction functional (2.2) with the series above. This results in the following iteration formula:
in the correction functional (2.2) with the series above. This results in the following iteration formula:
 (2.3)
(2.3)
3. New Imprved Variational Homotopy Perturbation Method
To illustrate the basic concept of the New Improved Variational Homotopy Perturbation Method, we consider the following general differential equation:
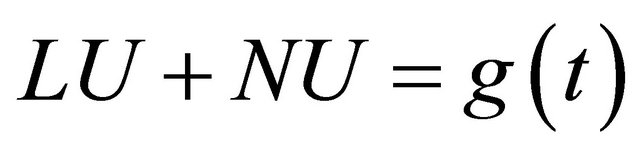 (3.1)
(3.1)
where L is a linear operator, N a non-linear operator, and 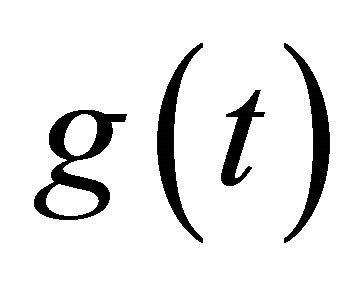 is the homogenous term. By the variational iteration method, we construct a correction functional :
is the homogenous term. By the variational iteration method, we construct a correction functional :
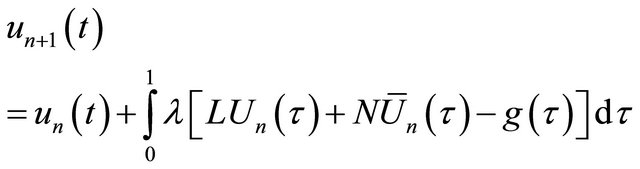 (3.2)
(3.2)
where 
Hence,
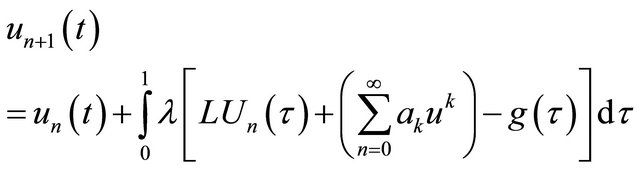 (3.3)
(3.3)
where 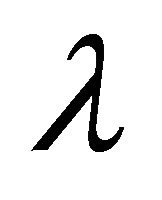 is a Lagrange multiplier according to Barari et al. [1], which can be identified optimally via variational theory. The subscript n denotes the n-th approximation,
is a Lagrange multiplier according to Barari et al. [1], which can be identified optimally via variational theory. The subscript n denotes the n-th approximation, 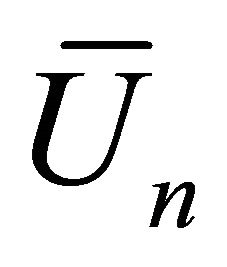 is considered as a restricted variational, that is,
is considered as a restricted variational, that is,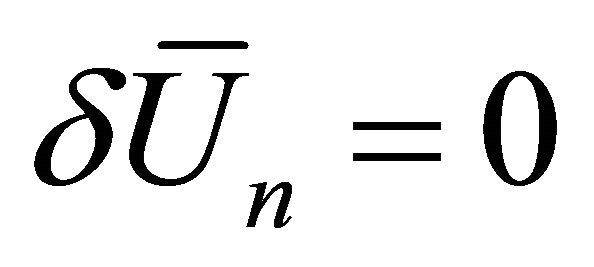 ; and Equation (3.2) is called a correction functional.
; and Equation (3.2) is called a correction functional.
Now we implement the New Improved Variational Homotopy Perturbation Method to the correction functional in Equation (3.3). we have the following:
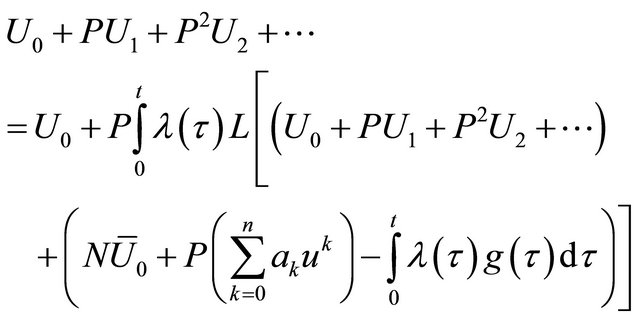 (3.4)
(3.4)
This can be expressed as:
 (3.5)
(3.5)
Hence, Equation (3.5) represents the coupling of variational iteration and Homotopy Perturbation methods.
The comparison of the coefficients of like powers of P gives solutions of various orders, this implies:
 (3.6)
(3.6)
4. Numerical Examples
In this section, we will apply the New Improved Variational Homotopy Perturbation Method for soving boundary value problems or Initial value problems of the Bratu-type equation. Numerical results are shown to illustrate the efficiency of the method.
Example 1: We consider the Bratu-type equation [12]
 (4.1)
(4.1)
with the boundary conditions

Based on the Taylor series of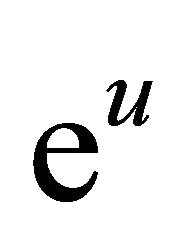 ,
,
 (4.2)
(4.2)
Correction functional is given is given as
 (4.3)
(4.3)
the NIVHPM is given as
 (4.4)
(4.4)
Comparing the coefficients of like powers of p, we have:
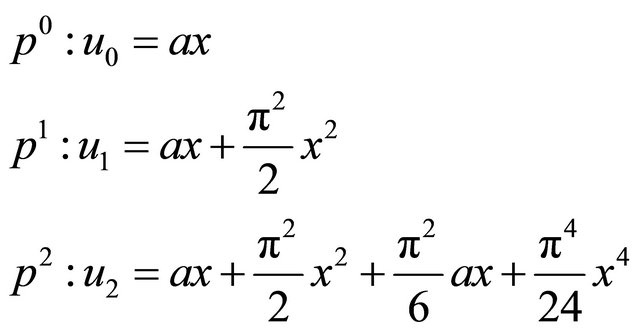
Example 2: We next consider the Bratu-type equation [12]
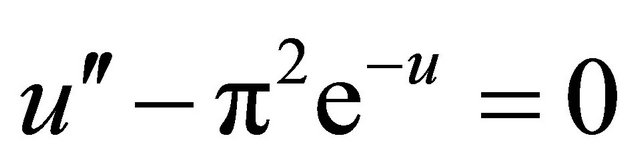 (4.5)
(4.5)
with the boundary conditions

Using the Taylor series of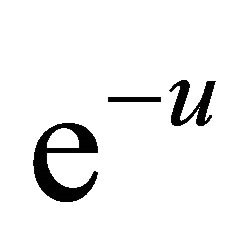 , the correction functional is given as
, the correction functional is given as
 (4.6)
(4.6)
the NIVHPM is given as
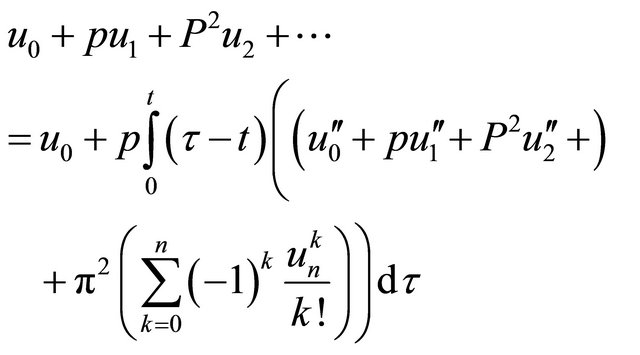 (4.7)
(4.7)
Comparing the coefficients of like powers of p, we have:

Example 3: We again consider the Bratu-type equation [9]
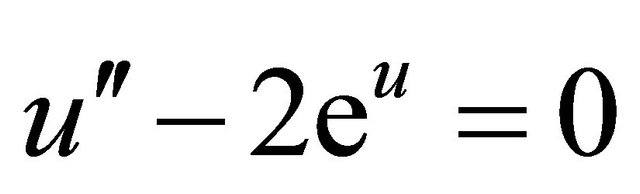 (4.8)
(4.8)
with the boundary conditions
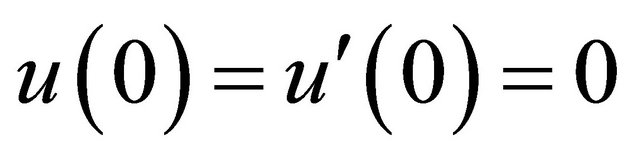
Using the Taylor series of , the correction functional is given as
, the correction functional is given as
 (4.9)
(4.9)
the NIVHPM is given as
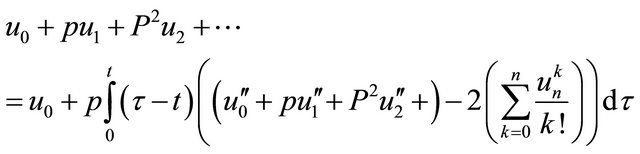 (4.10)
(4.10)
Comparing the coefficients of like powers of p, we have:
 (4.11)
(4.11)
5. Conclusion
In this paper, New Improved Variational Homotopy Perturbation Method has been successfully applied to find the solution of Bratu-type problem and the results obtained were compared favourably with the two convectional variational iteration and Homotopy Perturbation Method. It can be concluded that the NIVHPM is a very powerful and efficient technique for finding approximate solutions for wide classes of problems. It is worth mentioning that the Method is the computational cost friendly.
REFERENCES
- J. P. Boyd, “An Analytical and Numerical Study of the Two-Dimentional Bratu Equation,” Journal of Scientific Computing, Vol. 1, No. 2, 1986, pp. 183-206. doi:10.1007/BF01061392
- J. P. Boyd, “Chebyshev Polynomial Expansions for Simultaneous Approximation of Two Branches of a Function with Application to the One-Dimentional Bratu Equation,” Applied Mathematics and Computation, Vol. 142, 2003, pp. 189-200. doi:10.1016/S0096-3003(02)00345-4
- J. Jacobson and K. Schmitt, “The Liouville-Bratu-Gelfand Problem for Radial Operators,” Journal of Differential Equations, Vol. 184, No. 1, 2002, pp. 283-298. doi:10.1006/jdeq.2001.4151
- M. I. Syam and A. Hamdan, “An Efficient Method for Solving Bratu Equations,” Applied Mathematics and Computation, Vol. 176, No. 2, 2006, pp. 704-713. doi:10.1016/j.amc.2005.10.021
- A. M. Wazwaz, “Adomian Decomposition Method for a Reliable Treatment of the Bratu-Type Equations,” Applied Mathematics and Computation, Vol. 166, No. 3, 2005, pp. 152-633.
- X. Feng, Y. He and J. Meng, “Application of Homotopy Perturbation Method to Bratu-Type Equations,” Topological Methods in Numerical Analysis, Vol. 32, No. 2, 2008, pp. 243-252.
- L. Jin, “Application of Variational Iteration Method to the Fifth-Order KdV Equation,” International Journal of Engineering, Contemporary Mathematics and Sciences, Vol. 3, 2008, pp. 213-222.
- Z. M. Odibat, “Reliable Approaches of Variational Iteration Method for Nonlinear Operators,” Mathematical and Computer Modelling, Vol. 48, No. 1-2, 2008, pp. 222- 231. doi:10.1016/j.mcm.2007.09.005
- L. Jin, “Application of Modified Variational Iteration Method to the Bratu-Type Problems,” International Journal of Engineering, Contemporary Mathematics and Sciences, Vol. 4, 2010, pp. 153-158.
- J. H. He, “Homotopy Perturbation Method for Bifurcation of Nonlinear Problems,” International Journal of Nonlinear Sciences and Numerical Simulation, Vol. 6, No. 2, 2005, pp. 207-208.
- J. H. He, “Some Asymptotic Methods for Strongly Nonlinear Equations,” International Journal of Modern Physics B, Vol. 20, No. 10, 2006, pp. 1141-1199. doi:10.1142/S0217979206033796
- J. H. He, “Variational Iteration Method for Delay Differential Equations,” Communications in Nonlinear Science and Numerical Simulation, Vol. 2, No. 4, 1997, pp. 235- 236. doi:10.1016/S1007-5704(97)90008-3

