World Journal of Nuclear Science and Technology
Vol.07 No.01(2017), Article ID:73332,23 pages
10.4236/wjnst.2017.71004
Further Studies of BURSTS and Spallation in High-Energy Heavy Ion Reactions
Reza Hashemi-Nezhad1, Reinhard Brandt2, Valery Ditlov3, Maria Haiduc4, Elena Firu4, Alina Tania Neagu4, Eberhard Ganssauge5, Wolfram Westmeier6
1School of Physics, University of Sydney, Sydney, Australia
2Kernchemie, FB Chemie, Philipps Universität Marburg, Marburg, Germany
3Institute of Theoretical and Experimental Physics, Moscow, Russia
4Bucharest Institute of Space Science, Bucharest, Romania
5FB Physik, Philipps Universität Marburg, Marburg, Germany
6Dr. Westmeier GmbH, Ebsdorfergrund, Germany

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: November 17, 2016; Accepted: January 6, 2017; Published: January 9, 2017
ABSTRACT
Aspects of BURSTS and Spallation reactions induced by high-energy heavy ions in thick targets (>10 cm thick) will be investigated: BURSTS are reviewed from a historical and phenomenological point-of-view. Details of interactions in nuclear emulsions will be compared for irradiations of 72 GeV 22Ne-ions from Dubna with irradiations of 72 GeV 40Ar-ions from Berkeley. Measured correlations in individual interactions between multiplicities of “minimum ionizing particles”, ns, and “black prongs”, nb, will be shown as “ns-vs.-nb” per event for BURSTS and separately for Spallation in interactions of 72 GeV 22Ne-ions. Monte Carlo calculations, based on the MCNPX 2.7 code, have been carried out for 72 GeV 22Ne interacting in nuclear emulsions: The correlation between ns and nb in Spallation reactions could be understood. However, “ns-vs.-nb” correlations from BURST-interactions could not be reproduced with this model for events with small numbers of heavy prongs nh ≤ 10. For large numbers of heavy prongs with nh > 10 one could find some agreement between experiments and calculations, however, not in all details. Further experimental and theoretical studies are necessary before one has a complete understanding of BURST interactions in high-energy heavy ion reactions.
Keywords:
High-Energy HI Reaction, BURST, Spallation, MCNPX

1. Introduction
What is so exciting about BURSTS?―A historical and phenomenological review
In a preceding publication [1] , some aspects of BURST and Spallation reactions induced by high-energy heavy ions were presented. This contribution will describe some aspects of these reactions in more detail. It is a basic concept of this work [1] [2] that in high-energy heavy ion reactions above a threshold of Ecm/u ~150 MeV two dominant reaction channels are observed: BURST and Spallation. Experimental details have for example been observed with nuclear emulsions and Solid State Nuclear Track Detectors (SSNTD) irradiated with high-energy heavy ions. In emulsion and SSNTD energetic charged particles create tracks which can be studied with optical microscopes. Spallation reactions have been investigated for decades and they are described frequently: At least, one heavy nucleus with charge Z > 1 is observed among the relativistic projectile fragments [1] . A fast nuclear cascade is followed by slow nuclear evaporations from the residual target nucleus.
BURST reactions show exactly ZERO relativistic fragments with Z > 1. Relativistic fragments with Z = 1 are observed as shower prongs in the microscope and their number is called “ns”. They are due to a complete fragmentation of the projectile or projectile fragment and possibly also of part of the target nucleus into shower prongs. These shower prongs can be due to protons above an energy of 375 MeV or due to charged pions above an energy of 56 MeV. The average number of shower prongs  per event in BURSTS is several times larger than
per event in BURSTS is several times larger than 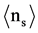 in Spallation reactions. Additionally, one observes also tracks from low energy protons with E < 26 MeV, called “black prongs”; their average number per interaction is
in Spallation reactions. Additionally, one observes also tracks from low energy protons with E < 26 MeV, called “black prongs”; their average number per interaction is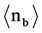 . One also observes some tracks from medium energy protons with 26 MeV < E < 375 MeV, called “grey prongs”; their average number per interaction is
. One also observes some tracks from medium energy protons with 26 MeV < E < 375 MeV, called “grey prongs”; their average number per interaction is . Finally, one considers “heavy prongs”, nh, defined as:
. Finally, one considers “heavy prongs”, nh, defined as:

BURSTS have been observed for more than 30 years. Obviously, they are due to a very drastic nuclear interaction of high-energy heavy ions, leading to the observation of very many prongs in one specific “star” within the nuclear emulsion. Only charged particles will produce a visible track in the emulsion, however, such an interaction MUST release simultaneously many free neutrons. These neutrons leave no track in the nuclear emulsion but they can induce secondary nuclear interactions yielding all kinds of conventional nuclear reaction products, which can be studied by nuclear chemists with their analytical methods [2] . Some earlier studies of BURSTS using nuclear emulsions and/or Solid State Nuclear Track Detectors (SSNTD) shall be recalled:
・ Khan et al. [3] observed in 1985: “Clusters of light tracks in a stack of CR-39 exposed to 980 MeV/u 238U”.
・ Ganssauge [4] observed a BURST-interaction produced by 980 MeV/u 238U in a nuclear emulsion, irradiated at the Bevalac accelerator in Berkeley (California), as shown in Figure 1(a).
・ Tolstov [5] showed a “very drastic” and “peculiar” event. It was produced in a nuclear emulsion irradiated with 72 GeV 22Ne ions at the Synchrophasotron accelerator in Dubna (Russia) as shown in Figure 1(b). In this reaction, both the projectile and target are completely disintegrating into single nucleons plus pions. No tracks from Z ≥ 2 particles are visible. One should also note the track-free angle of 14 degrees in the forward direction.
BURST-interactions need further experimental investigations and a concept in order to understand this nuclear reaction path better. As we do not understand BURST events, we cannot order experimental results according to model topics but we can only list them. There clearly are unresolved problems in BURST reactions.
1) Fundamental aspects, which could be investigated with nuclear emulsions and SSNTDs are:


Figure 1. (a) BURST-interaction of 960 MeV/nucleon 238U ion in nuclear emulsion. The irradiation was made at the Bevalac accelerator in Berkeley (California) [4] . (b) This “peculiar” BURST event was observed in a nuclear emulsion by Tolstov [5] . It was produced by 72 GeV 22Ne-ions at the Synchrophasotron accelerator in Dubna (Russia). Note the empty angle (14˚) in forward direction. The picture is a projection of the 3D distribution onto the image plane over a limited track length.
・ More accurate angular ns track-distributions are needed at small angles with respect to the beam direction; they must be measured and should be compared to model calculations. In table 4 of Ref. [1] is shown evidence induced by 72 GeV 22Ne ions; it shows that 364 events out of the total ensemble of 1011 events (36%) have an open angle in the straight forward direction. Tolstov has observed a similar effect for 19 events (private communication, M.H.).
・ There are no theoretical model calculations known to the authors that can explain the entire BURST-interaction or the special case of the “open gap at zero-degree”. An attempt on BURSTS based on Monte Carlo code MCNPX 2.7 will be presented in this paper.
・ Due to lack of experimental knowledge of the energy carried by a single particle, one cannot attempt at this stage an estimate of the total energy balance in individual BURST interactions.
2) Practical aspects of using BURSTS to solve problems in a specific area of technical applications are:
When one looks into Figure 1(a), one observes a picture of a nearly complete destruction of a uranium nucleus into about 92 tracks, all being from Z = 1 hadrons. Simultaneously, there must have occurred a emission of up to 146 high- energy neutrons. The open question is: can such a process be of use for mankind in any way?
2. The Ratio of BURSTS-to-Spallation for Two Generations of Interactions
2.1. Observations in Nuclear Emulsions Irradiated with 72 GeV 22Ne in Dubna (Russia)
Experimental observations are shown in a schematic form for the reaction of 72 GeV 22Ne in Figure 2 which is based on Ref. [1] (see Ref. [6] for experimental
Figure 2. The history of BURST and spallation for a sequence of two generations in nuclear emulsions irradiated with 72 GeV 22Ne. Details are described in the text.
details): In the emulsion one follows the path of 1093 primary ions (72 GeV 22Ne). A large portion of these primary ions, exactly 666 ions, leave the emulsion without interacting and only 427 ions induce a first interaction yielding 112 BURSTS (BUR) with an average number of black prongs 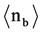 = (11.83 ± 0.33) and 315 Spallations (SPA) with an average number of black prongs
= (11.83 ± 0.33) and 315 Spallations (SPA) with an average number of black prongs  = (4.38 ± 0.12). BURSTS produce only Z = 1 relativistic projectile fragments, their paths in the emulsion are no longer followed in this study.
= (4.38 ± 0.12). BURSTS produce only Z = 1 relativistic projectile fragments, their paths in the emulsion are no longer followed in this study.
This investigation follows the second generation of interactions of the above mentioned 315 Spallation products. 173 of these tracks leave the thin emulsion without further interaction and only 142 particles induce an observable second interaction. We observe 100 BURSTS (BUR) with an average number of black prongs 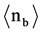 = (7.9 ± 0.3), and 42 Spallations (SPA) with an average number of black prongs
= (7.9 ± 0.3), and 42 Spallations (SPA) with an average number of black prongs 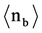 = (4.74 ± 0.34).
= (4.74 ± 0.34).
A more detailed presentation is given in Figure 2 (lower part) to describe the second interaction of the above mentioned 142 particles: 72 of these Spallation- tracks are from alpha-particles (Z = 2) and these particles induce 66 BURSTS (BUR), having an average number of black prongs 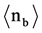 = (7.24 ± 0.33) plus only 6 Spallations (SPA). The other 70 Spallation interactions are from particles with Z > 2. These particles produce 34 BURSTS (BUR) with an average number of black prongs
= (7.24 ± 0.33) plus only 6 Spallations (SPA). The other 70 Spallation interactions are from particles with Z > 2. These particles produce 34 BURSTS (BUR) with an average number of black prongs 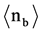 = (9.24 ± 0.52), and 36 Spallations (SPA) with an average number of black prongs
= (9.24 ± 0.52), and 36 Spallations (SPA) with an average number of black prongs 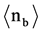 = (4.39 ± 0.34).
= (4.39 ± 0.34).
Figures 3(a)-(c) present event frequencies of BURST- and Spallation reactions

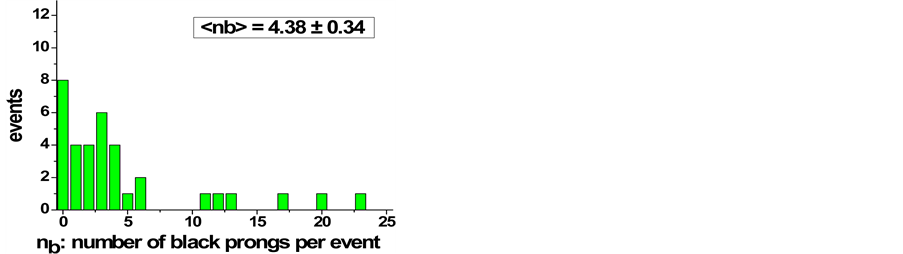
Figure 3. (a) Spectrum of black prongs from 66 BURST interactions produced by Z = 2 spallation fragments in the second generation. (b) Spectrum of black prongs from 34 BURST interactions produced by Z > 2 spallation fragments in the second generation. (c) Spectrum of black prongs from 36 spallation interactions produced by spallation fragments in the second generation.
in the second generation of interactions as a function of nb. Separate distributions are shown for BURSTS induced by Z = 2 and Z > 2 particles.
The study of the third generation of interactions of Spallation products could have been made for only 11 tracks that lead to a third interaction, whilst 31 tracks of this generation are leaving the emulsion layer without interacting. None of the 11 particles have been followed in this analysis.
In summary one observes:
・ The ratio BURST/Spallation interactions increases significantly from 112/315 = (0.36 ± 0.04) in the first interaction to 100/42 = (2.4 ± 0.3) in the second interaction. This increase by a factor of 6.7 of BURST interactions in the second generations is a highly surprising finding.
・ The average numbers of black prongs 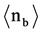
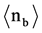

・ Of particular interest are the 72 Spallations in the second interaction due to alpha-particles (Z = 2). These alphas lead in 66/72 (=92%) cases to BURSTS. This must be compared to “standard-model” reactions when relativistic alpha particles are projectiles: These latter ones yields BURSTS in only 7% ± 1% of all interactions (Ref. [1] ).
A compilation of multiplicities in the first two generations is given in Table 1. BURST reactions are clearly favored to happen in second interactions, especially when induced by relativistic helium (Z = 2) nuclei. It is apparent that in BURST reactions plenty energy is involved as the nucleus completely disintegrates into single nucleons, however, one finds more low-energy protons (nb) in BURST than in Spallation reactions. The number of low-energy protons of BURSTS is always larger than nb of Spallation. This experimental finding is not expected from nuclear models.
2.2. Observations in Nuclear Emulsion Irradiated with 72 GeV 40Ar in Berkeley (California)
Nuclear emulsions were irradiated with 72 GeV 40Ar from the BEVALAC at the LBNL in Berkeley and studied by Haiduc and Lerman; data are published in part as a Ph.D. Thesis [8] :
Table 1. 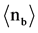
(*) published in Ref. 1 including spectra for nb, according to Ditlov et al. [6] [7] . (+) graphical presentations are shown above in Figures 3(a)-(c).
A compact stack of nuclear emulsions was irradiated with 72 GeV 40Ar ions, developed and systematically analyzed. The fate of 817 tracks from the primary ions (72 GeV 40Ar) was followed inside the emulsion stack for 5 generations of consecutive Spallation interactions for all Z > 1 secondary tracks; data are presented in Table 2 “Generation of Secondaries by Charge”. The results for BURST-interactions have not been published in the Thesis [8] .
This presentation of interactions of projectile-like fragments―i.e. using the terminology of this paper for “Spallation interactions”―in nuclear emulsion shows the following characteristics:
GENERATION 1: Obviously, one registers 817 events from 72 GeV 40Ar with Z = 18.
GENERATION 2: One considers ONLY projectile-like events with Z > 1. Only these Spallation interactions (or: projectile-fragments) are counted and BURST interactions are completely neglected. One observes 490 events with Z = 2 (alpha particles) and 467 events having 3 ≤ Z ≤ 18.
It is interesting to note that the ratio of reactions induced by Z = 2 fragments over Z > 2 fragments is almost identical; in 72 GeV 22Ne + em it is 72/70 = 1.03 and in 72 GeV 40Ar + em it is 490/467 = 1.05. Fragments having charges 1 or 19 have not been determined unambiguously; therefore their numbers are erased from Table 2.
Table 2. (copy from Ref 8, page 4 - 13) Multiplicities of projectile-like fragments having nuclear charge 2 ≤ Z ≤ 19 in five consecutive generations of interactions of 72 MeV 40Ar in emulsion. Data for Z = 19 in generation 2 are erased from the table as this number was not unambiguously determined.
GENERATION 3: One observes strongly reduced numbers for all projectile-like fragments. Only 178 events from Z = 2 (alpha) and 129 events from 3 ≤ Z ≤ 18 are observed.
GENERATION 4: Continuing the considerations for GENERATION 3 one finds a steady decrease of the observed number of Spallation-like interactions induced by Z > 1 fragments.
GENERATION 5: In the last generation Spallation reactions have nearly completely vanished due to a lack of kinetic energy of projectiles. Almost all generation 5 Spallation reactions are induced by helium projectiles.
3. Three Dimensional Correlations for “ns-vs.-nb” for BURSTS and Spallation Interactions of 72 GeV 22Ne Interactions in Nuclear Emulsion
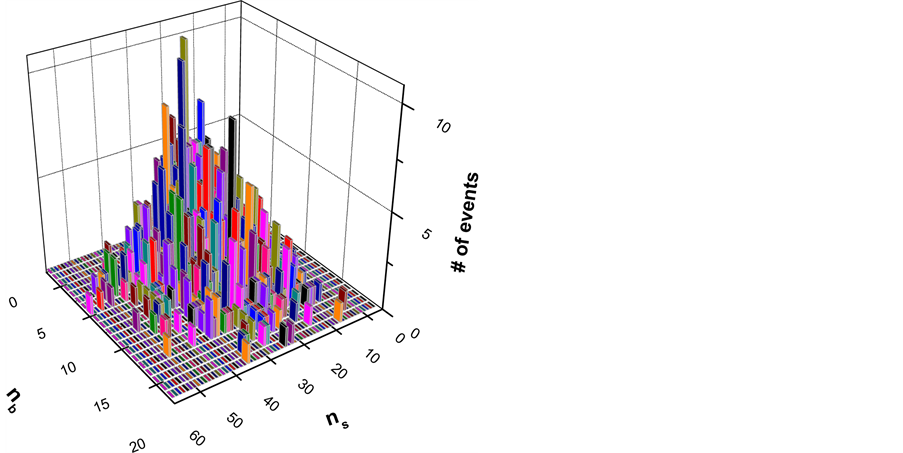
Haiduc et al. [9] have measured further details in 3292 Spallation-events from 72 GeV 22Ne on nuclear emulsion. They counted the number of black prongs, nb, and minimum ionizing particles, ns, for each event and obtained a data-set with a “nb-versus-ns” information for all 3292 Spallation events. They reported the actual nb-value, i.e. the number of black prongs with energy below 26 MeV. They did NOT include grey prongs, ng, with proton energy [26 MeV < E(ng) < 375 MeV]. This “ns-vs.-nb” data-set is shown for all 3292 Spallation events in Figure 4 in a 3-dimensional representation.
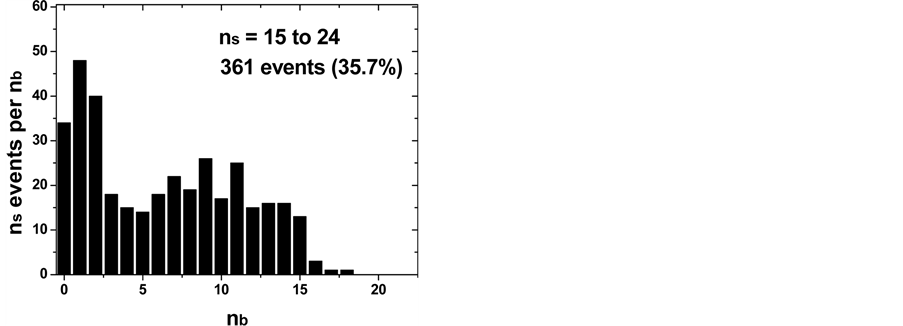
Figure 5 gives another and more detailed picture of the same information; it shows three two-dimensional correlations for different regions of ns. In the low ns-region between (0 ≤ ns ≤ 14) one finds 82.2% of all Spallation events, in the higher ns-regions correspondingly less. The maximum of events are close to small values of nb and ns, or more quantitatively: this maximum is found at 0 ≤ nb ≤ 5 and 0 ≤ ns ≤ 15. For Spallation, one observes in this small center
Figure 4. The nb-vs.-ns correlation plot for 3292 spallation events from interactions of 72 GeV 22Ne in nuclear emulsion.
Figure 5. 3292 spallation events presented as ns-vs.-nb correlations for different ns regimes. Data are based on M. Haiduc’s measurement of 72 GeV 22Ne-interactions in nuclear emulsion.
around the origin of the coordinate system approx. 66% of all events.
Haiduc et al. also investigated with the same technique 1011 first generation BURST-events from 72 GeV 22Ne-interactions in nuclear emulsion and registered for each event the “nb-vs.-ns” data-set.
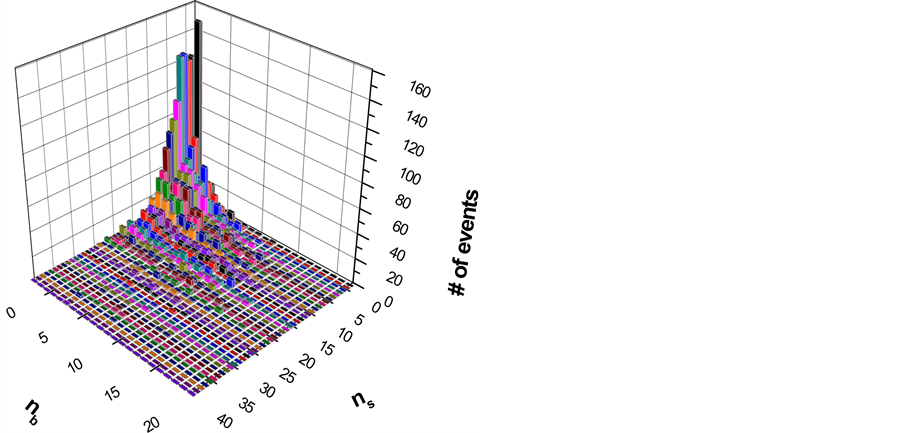
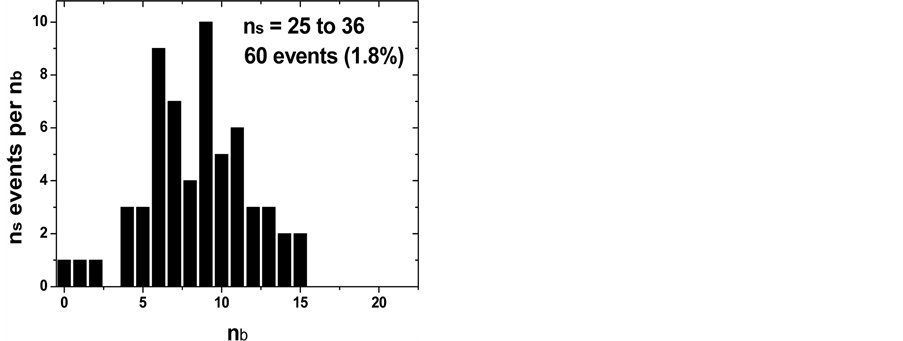
The results are plotted as “nb-correlated-ns” data set for BURST events in Figure 6. Figure 7 gives again the more detailed picture of the same information; it shows three two-dimensional correlations for different regions of ns. In the low ns-region between (0 ≤ ns ≤ 14) one finds only 8.3% of all BURST events, in the large ns-regions (25 ≤ ns ≤ 60) correspondingly the largest number of 56.0% BURST. These two correlation plots for Spallation and BURST reactions are completely different: For BURSTS one finds in the area 0 ≤ nb ≤ and 0 ≤ ns ≤ 15 (around the origin of the coordinate system) only 52 (5%) out of all 1011 events. The other 959 events are found within a wide area of the diagram up to nb ≤ 20 and ns ≤ 60.
In short: Spallation reactions yield small values of nb (low-energy particles) and ns (high-energy particles) whereas in BURST reactions multiplicities of both low- and high-energy particles are significant.
Theoretical studies on the BURST phenomenon are presented in the next section.
Figure 6. The nb-vs.-ns correlation plot for 1011 BURST events from interactions of 72 GeV 22Ne in nuclear emulsion.
Figure 7. 1011 BURST events presented as ns-vs.-nb correlations for different ns regimes. Data are based on M. Haiduc’s measurement of 72 GeV 22Ne-interactions in nuclear emulsion.
Figure 4 shows that the distribution of events in the ns-vs.-nb space is essentially centered around ns = 0 and nb = 0. This is expected for Spallation reactions where relatively little energy is involved and one does not expect large numbers of particles in the output channel. A more detailed sketch of the same data is shown in Figure 5 where ns multiplicities are shown as function of nb for different ns-regimes. The lower ns-distribution for ns £ 15 is strongly peaked around nb = 0 and it looks like a “Spallation” distribution. In the middle-ns regime from ns = 15 to 24 one finds a two-peaked distribution which looks like a mix of Spallation and BURST, whereas in the high-ns regime one finds most events around larger numbers of nb. An increasing number of ns go with an increasing number of nb.
Figure 6 shows the nb-vs.-ns correlation for BURST reactions. Its display is very different from the Spallation distribution in Figure 4 in that most events are distributed to higher values of nb and ns, i.e. there is significantly more energy in the system.
Details of the distribution are shown in Figure 7 which is equivalent to Figure 5. In contrast to the Spallation distribution there are only very few events in the small ns regime whereas the majority of events is found at large numbers of ns.
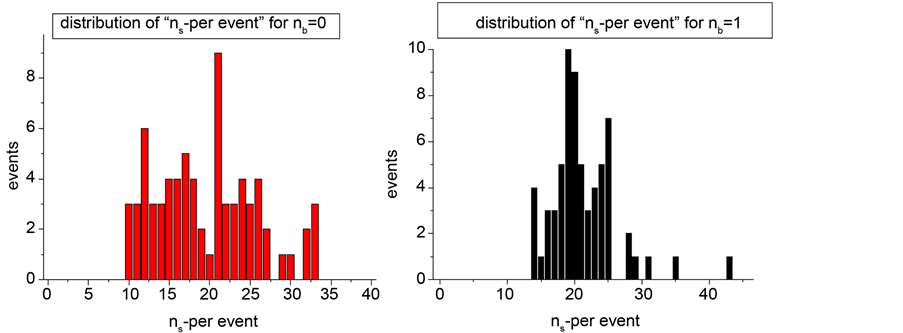
It is also interesting to look into another detail of Figure 7 and to study individually the observed ns-events (i.e. relativistic particles) for BURST interactions having only nb = 0 (73 events) or nb = 1 (65 events). The result is shown in Figure 8.
For nb = 0 one observes a broad distribution of events having ns = 10 to ns = 33. In these 73 events one finds a total of 1420 minimum ionizing particles (ns = 1420) which are associated with zero black prongs (nb = 0). This happens in 73/1011 = 7.2% of all BURST events.
A very similar situation is found for 65 events having nb = 1 in which a total of 1388 minimum ionizing particles are measured. In total, the ratio nb/ns for these 138 events of 65/2808 = 0.023 is significantly lower than the observed overall ratio [1] of nb/ns = 0.28.
Thus, very small numbers of low-energy particles as seen in 138 events (nb = 0
Figure 8. Experimental frequency distribution of events with ns relativistic charged particles in the exit channel which are associated with zero or only one low-energy particle nb per BURST interaction. Note that there are no events with less than 10 relativistic protons. In total one finds138 BURST events (13.6% of all BURSTS) which have only 65 black prongs (nb) together with 2808 shower tracks (ns).
or 1) are associated with 2808 relativistic particles. In all cases, even at very small nb, there are at least 10 relativistic particles seen in the exit channel because BURST events are selected. Such distribution of very many high- and very few or even no low-energy particles in the exit channel have not been predicted by the model (see next section). The calculated numbers of low-energy particles per one relativistic particle are typically almost twice as large as experimentally observed for BURST events.
It should be noted that one can clearly see very small numbers of black prongs (nb = 0 or 1) in an interaction in emulsion and an incorrect assignment of such events can be excluded.
4. Monte Carlo Simulations of BURST Events
In this section, we report results of an attempt to simulate BURST events using MCNPX 2.7 Monte Carlo code [10] . MCNPX is not designed for this type of calculations, however, due to its flexibilities and availability of many options in the code it is possible to simulate interactions of the relativistic ions with nuclear emulsion event by event.
When using the Monte Carlo method to simulate BURST interactions one has to find the proper and well-defined boundary conditions in order to simulate the observed physical reality. The BURST definition used in this paper and in Ref. [1] does not have such a unique and fixed number of interacting and participating particles. Therefore the authors have to employ a slightly modified definition for BURST interactions in the Monte Carlo calculation with the MCNPX 2.7 code.
Definition: BURSTS are relativistic heavy ion interactions in which the heavy projectile totally fragments into Z = 1 particles and neutrons and no relativistic fragments with Z > 1 are produced
The above-mentioned definition of BURST events implies that:
1) No relativistic projectile-fragment has a charge Z > 1.
2) Charged projectile fragments (Z = 1) can be relativistic and non-relativistic, i.e. they can produce shower and heavy prongs in the emulsion.
3) Target fragments can have any charge less than target nucleus charge (Z < ZT) and in the emulsion they can result in shower, and heavy prongs.
4) In the case of the Ne + emulsion interactions BURST events (as defined above) must have;
a) Greater than ten Z = 1 prongs, resulting from total fragmentation of the Ne and thus total number of prongs in such events must be nt ³ 10.
b) The net charge carried by the fragments must be nq > 10.
c) Number of neutrons released in a BURST interaction must be greater than 12 (number of neutrons in 22Ne). This condition is an approximation because during the nucleon-nucleon collisions which lead to pion production the type of nucleons may change.
In studies of nuclear reactions, to achieve acceptable statistical uncertainties the Monte Carlo (MC) codes usually run for a large number of histories (incident ions) and the final output of the code is normalized to the number of histories. In high-energy heavy ion interactions, such outputs cannot provide accurate information about the individual interactions. The events recorded in nuclear emulsion are due to individual interactions i.e. one projectile interacts with one target nucleus. Therefore, in order to simulate and understand events recorded in emulsion one must execute the MC-code and recoded interactions, event by event, as is the case in the emulsion experiments.
In this work the MCNPX 2.7 code [10] was used to simulate interactions of 4.1 AGeV/c 22Ne ions with emulsion. MCNPX transports the incident ion until its energy drops (because of energy loss due to electronic and/or nuclear interactions with the target atoms/nuclei) below a cut-off energy or the ion escapes the target surface after nuclear and/or electronic interactions. An incident ion and its fragments may make more than one nuclear reaction with the target nuclei. In order to simulate the events initiated by the incident ion in emulsion one needs to
・ Isolate individual primary projectile ion interactions.
・ Obtain particle yield and energy spectra of the each type of the product particles in each ion nucleus collision.
The obtained particle yields and spectra must not be contaminated by:
・ The particles produced from interactions of the projectile fragments.
・ The particles produced in interactions of the secondary particles.
Therefore, one wants to record only those particles that are produced in intra-nuclear cascade, pre-equilibrium and evaporation stages of the interactions of the primary ions. These are the particles recorded in the emulsion as prongs of an event. In order to reduce and possibly eliminate the number of secondary particle interactions, the emulsion dimension along the beam line must be reduced. It is shown that for L = 0.5 cm the contribution of secondary particle interaction products is negligible [11] .
It should be noted that in the calculations all charged particles (i.e. protons, deuterons, tritons, 3He, 4He and charged pions) are considered to yield measurable prongs regardless of their energies (track length) and total number of prongs present in an event is identical to the number of charged particles in the output channel. This may not be necessarily the case in the experimental measurements [11] where due to track identification and measurement limitations not all tracks may be measureable, in particular in events which are composed of many tracks. Such an underestimation of the track numbers may be more pronounced in the case of the black prongs which have short ranges.
(However, experimentalists are certain that in the measurements the number of tracks can be counted very accurately).
Details of the Monte Carlo simulations of heavy ion interactions with nuclear emulsion using the MCNPX 2.7 code are given elsewhere [11] .
Simulation of BURST events
A total of 10,146 individual inelastic interactions of 4.1 AGeV/c 22Ne with Ilford-G5 emulsion were recorded. In selecting the BURST events, the following conditions were imposed and only events which satisfied all of the following conditions were selected:
1) Events with Z ≥ 2 shower tracks were removed. The Z = 2 relativistic particles most likely result from projectile fragmentation and appear in 9% of the all events.
2) Events with charge release nq ≤ 10 were removed. Such events cannot belong to total fragmentation of the projectile (Z = 10).
3) Events with nq > 57 (total charge available in input channel) were removed. Such events are those in which interactions of the secondary particles were contaminating the results. There were only 9 out 10,146 event that had nq > 57 (i.e. less than 0.09%), suggesting that contamination of the prong numbers by particles from interactions of secondaries was insignificant.
4) Events with total track number nt < 10 were removed. In the total fragmentation of the Ne projectile one expects to find at least 10 prongs from the released charged particles plus those resulting from target fragmentation.
5) Events in which the number of released neutrons was less than 12 were removed.
After imposing all above mentioned five selection criteria 3292 events remained for which distributions of the numbers of shower, grey and black prongs per event were produced. It was found that the mean number of shower prongs per event is ~18 as compared to experimental value of ~26 (see Ref. [1] ). Such a disagreement is an indication that the above mentioned five filtering steps were not sufficient for an adequate separation of the BURST from Spallation events. This is mainly due to the fact that in the selection criteria the fragmentation of the target nucleus is not taken into account.
In order to match the mean number of shower prongs per event in simulated events with that of the measurements two different options were investigated:
4.1. Pion Track Number Limitation
The 3292 selected events were sorted in ascending order with respect to the total number of pion prongs (sum of the shower, grey and black) per event. Events were then removed from top of the list until the mean number of the shower prongs per event in the remaining events became as close as possible to the experimentally obtained value. The logic for imposing this condition is that; events in which the projectile totally fragments, the impact parameter must be less than that of Spallation reactions. In such ion-nucleus collisions, more nucleon- nucleon collisions takes place and thus on average more pions are produced. This filtering process imposes the condition that in the BURST events the total number of pion prongs must be greater than 16 for the case of Ne + Emulsion interactions. After this filtering 1666 events remained for which the mean num-
ber of shower prongs per event was 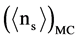
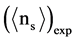
After the selection of BURST events from 10,146 recorded interactions, the remaining 8480 events were considered to be Spallation events.
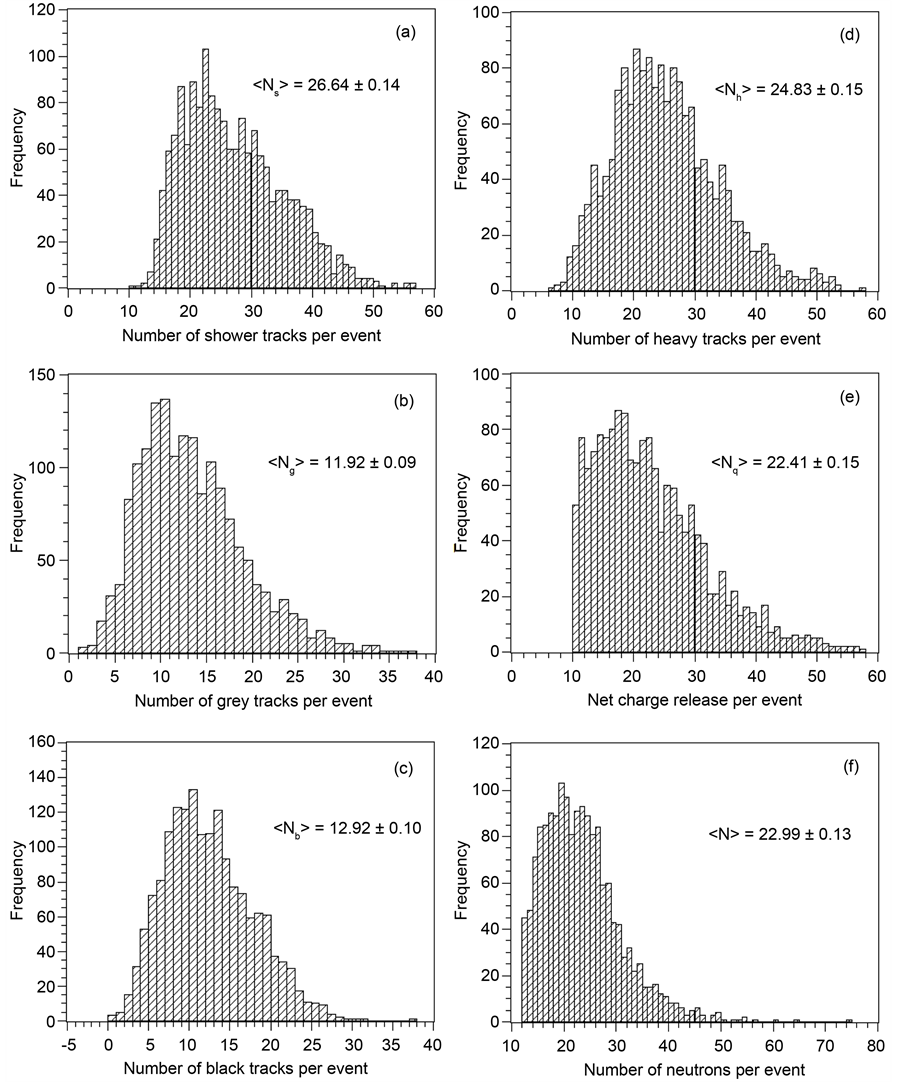
Figure 9 and Figure 10 show the calculated distributions of number of shower (ns), grey (ng), black (nb), heavy prongs (nh) prongs per event, net charge (nq) carried by the track producing particles per event as well as the distribution of the neutrons released per simulated BURST and Spallation events, respectively.
Figure 9. Distributions of different types of tracks (prongs), charge and neutron release in simulated BURST events in interactions of 4.1 AGeV/c 22Ne with nuclear emulsion: (a) shower prongs (ns), (b) grey prongs (ng), (c) black prongs (nb), (d) heavy prongs (nh), (e) net charge (nq) carried by the particles in the exit channel per event and (f) neutrons released per BURST event (N).
Figure 10. Distributions of different types of tracks (prongs) in simulated spallation events in interactions of 4.1 AGeV/c 22Ne with nuclear emulsion: (a) shower prongs (ns), (b) grey prongs (ng), (c) black prongs (nb), (d) heavy prongs (nh), (e) net charge (nq) carried by the particles in the exit channel per event and (f) neutrons released per Spallation event (N).
The term “Track producing particles” refers to protons, pions, deuterons, tritons and helium nuclei.
Comparison of the Simulation Results with Experiments
We believe that the selection criteria used in this MC-calculation do not yield a clean separation of BURST and Spallation events, however, comparison of the simulation results with the emulsion experiments would be educational and beneficial for future simulation works.
Table 3 gives the simulated and experimental numbers of the BURST and Spallation events in interaction of 4.1 AGeV/c 22Ne with emulsion.
From Table 3 it is evident that the agreement between calculation and experiment considering the number of BURST and Spallation events is not impressive, even bearing in mind that the number of the experimental events for “Experiment I” is small and statistical uncertainties are expected to be relatively large.
It should be noted that in the MC calculation all inelastic interactions of the projectile with target nuclei are taken into account as long as charged particles (regardless of their numbers) are produced; this may not have been the case in the experiments. Considering all inelastic interactions as events, increases the total number of the events, especially those with low number of prongs and low net charge release. This will lead to underestimation of the relative number of the BURST events in the calculations.
In Table 4, experimental findings of on 
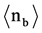
From the data given in Table 4, one cannot reach to a clear conclusion on agreement or disagreement of calculations with the experiments. While the calculation results are in reasonable agreement with experimental findings of [7] for 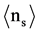
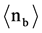
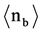
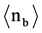
There are further differences between experiments and calculated BURST events:
Table 3. Comparison of the calculated and experimental results (i.e. events) in the interaction of 4.1 AGeV 22Ne with nuclear emulsions.
Table 4. Comparisons of the experimental values of mean numbers of the shower 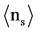

1) A detailed look at the experimental distributions of nb in Figure 3 and Figure 4 of Ref. [1] shows a number of events in which the number of black prongs is less than 5. The nb of these events may represent a pseudo-peak in the experimental nb distributions of the BURST events. Although in the calculated nb- distribution (Figure 10(c)) there are events with nb £ 5 but they are seen as part of the main distribution and do not represent a separate peak.
This difference may have two origins;
・ Calculation has failed to predict a peak at low nb values of the BURST events.
・ In the experiments a small fraction of the black prongs are mislabled. Dgbrowska et al. [12] state that “The experimental separation between grey and black tracks is somewhat subjective”. Thus in experiments some fraction of the grey tracks may have been labelled as black or vice versa, as also mentioned in Refs. [6] and [7] .
At present, we cannot vote in favor of any of the above mentioned two scenarios.
2) Another difference is also significant. The experimental heavy prong distribution is shown in Figure 11. It can be compared with the calculated distribution from Figure 9(d). The experimental distribution shows two maxima around nh = 6 and nh = 28. The calculated distribution has only one maximum around nh = 24.8. The calculated distribution has practically no events (<1%) below nh = 10, however, the experiment shows that ~20% of all BURSTS are observed below nh = 10. The authors consider these ~20% of all BURSTS as not being compatible with the calculation method presented in this paper. This finding may be connected with “unresolved problems” discussed earlier [1] [2] [13] .
Figure 11. Experimental distribution of “heavy tracks” (nh = ng + nb) for BURST events in the interaction of 72 GeV 22Ne in nuclear emulsion. There is a break around nh = 10 which separates observable events below which are not predicted by the model calculations presented in the work.
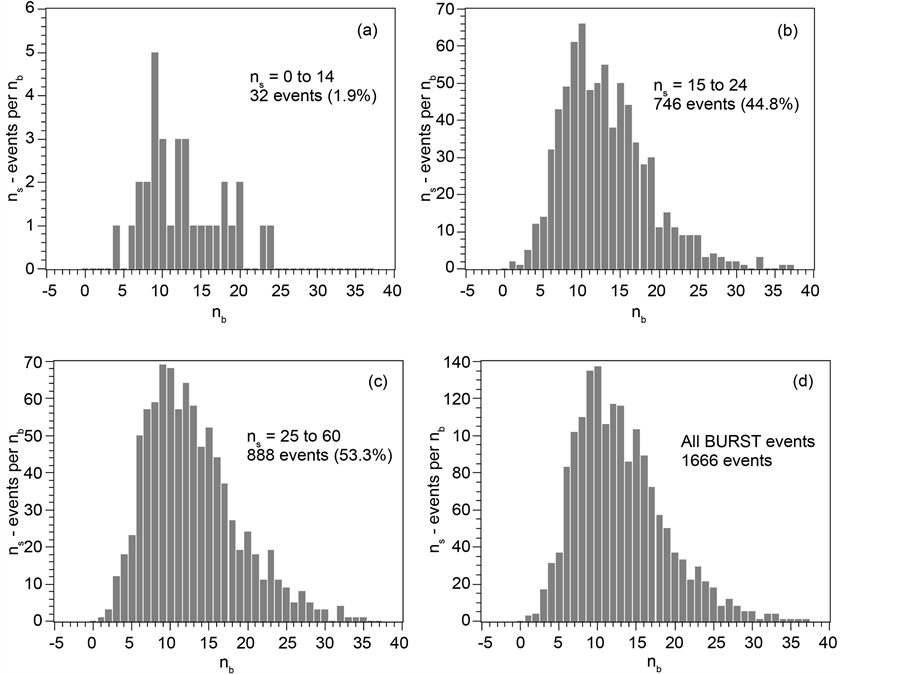
Another detail is given in Figure 12. It shows “ns-versus-nb” correlations for 1666 calculated BURST events in interactions of 72 GeV 22Ne ions with emulsion. In the insert of this figure the percentages of the events belonging to a given ns interval of the BURST events are given. These percentages are not in agreement with the corresponding values in the experiment for ns intervals of 0 to 14 and 15 to 25. However, for the ns interval of 25 to 60 experiment and calculations are in reasonable agreement. The shapes of distributions in Figure 12(b) and Figure 12(c) are different from their corresponding distributions in the experiment (Figure 7) in that the calculated distributions have always only very few events below nb < 5 whereas the experimental distributions have significant numbers of events with nb < 5. The calculated correlations in Figure 12(b) and Figure 12(c) have their only maximum around nb ~ 10. Two experimental maxima in the corresponding Figure 7 have been measured around nb = 2 and nb = 8.
These observations could suggest that in the filtering process of the BURST event selection, some of the events with low nb have been removed unjustifiably.
4.2. Heavy Track Number Limitation
The 3292 selected events (as described in Sec. 4) were sorted in ascending order
Figure 12. “ns-vs.-nb” correlations for 1666 calculated BURST events in the interaction of 72 GeV 22Ne ions with a nuclear emulsion. In the insert of figures (a) to (c) the percentage of events belonging to the given ns-interval are listed. Details are given in the text.
with respect to the total number of heavy prongs per event. Events were then removed from top of the list until the mean number of the shower prongs per event in the remaining events became as close as possible to the experimentally obtained value (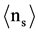
In interaction of relativistic ions with nuclear emulsion the events with nh ≥ 28 are referred to as events in which Total Destruction (total disintegration, total fragmentation) of the target nucleus Ag(Br) takes place (TD events). In Refs. [14] [15] , TD events are described as: “in central collisions of fast particles with heavy nuclei, events containing Nh ≥ 28 heavy prongs in standard emulsion may be considered as central collisions with Ag(Br). These events are complete destruction of the target nucleus with no observable residual nucleus with a measurable mass”.
Monte Carlo simulations related to TD events are discussed in detail in another publication [11] .
After imposing the nh-limit 631 events remained, suggesting that nh-limit selects only a special type of the BURST events. This finding leads to an important conclusion that: a significant number (~38%) of BURST events accompanied with total destruction of Ag(Br) in the emulsion, i.e. in these events BURST and TD events take place in conjunction. These events may be referred to as BURST-TD events. If we generalize this observation to all BURST interactions, we may conclude that the majority of the BURST interactions are accompanied with total destruction of a target nucleus in the emulsion (i.e. C, N, O, S, Br, Ag and I).
5. Conclusions
This paper presents additional information which shall help to come closer to the understanding of “unresolved problems” in heavy ion interactions in thick targets [16] above an energetic threshold of ECM/u ≈ 150 MeV [2] and to understand BURSTS [1] in the same context.
・ BURST reactions are a major nuclear reaction channel when high-energy projectiles interact with a target. This is especially true for the second generation of interactions in general and in particular when relativistic secondary Z = 2 (helium) nuclei make another interaction.
・ From the fact that the number of low-energy charged particles (nb) emitted in a BURST reaction is significantly larger than nb in Spallation reactions one can deduce that there is significantly more energy involved in BURSTS than in Spallation.
The same arguments is supported by the finding that in most Spallation reactions a small number of relativistic fragments is emitted (0 ≤ ns ≤ 14) whereas the number of relativistic fragments is BURST reactions in most cases is large (ns > 24).
・ The 3-dimensional probability distribution of low-energy fragment (nb) vs. relativistic high-energy fragment multiplicity (ns) shows that Spallation reactions yield small numbers of fragments whereas in most BURST reactions a larger number of fragments is emitted.
・ In BURST reactions one does not find a single event where none or only one low-energy particle (nb) is emitted together with less than 10 relativistic particles (ns).
The Monte Carlo calculations were performed using MCNPX 2.7 code. The current form of the code does not allow full definition of the BURST events to be implemented in the simulations. This arises mainly from the fact that one cannot separate the projectile and target fragment from each other which is essential for the BURST definition. Therefore an event filtering method with some assumptions was used to select BURST events from 10,146 recorded inelastic events from the interaction of 72 GeV 22Ne ions with nuclear emulsion (as described in Sections 4.1 and 4.2).
The method given in Section 4.1 yields mixed results when compared with two sets of experimental findings as shown in Table 3 and Table 4.
The BURST event selection criteria given in Section 4.2 select a special type of the events in which BURST events are accompanied by total destruction of AgBr in emulsion. For this type of interactions, the distributions of multiplicities of the special BURST events are not given in this paper, because they look very similar to the TD events as presented in Ref. [11] .
The calculated results show that Spallation reactions in the interaction of 72 GeV 22Ne in nuclear emulsion are understood as calculated Spallation results match the experiments well.
One cannot exclude that the differences mentioned above come from peculiarities that happen in the second and following generations of interactions.
From the findings in Ref. [2] and observation of the highly increased rate of the BURST events in the second generation (Figure 2), it is clear that relativistic secondary particles interact more efficiently with the next target nucleus than a primary particle does. It looks as if the secondary particle is bigger, at least for a short while, after the first interaction. Such observation is definitively not in agreement with standard models of physics and is not expected to be predicted by the Monte Carlo simulations; it needs further studies to understand these experimental findings.
At this level of limited knowledge, it is too early to discuss any technological application using the “enhanced destruction capabilities” of secondary fragments [17] .
More detailed simulations of the BURST events (as defined in this paper) are required, and we invite other authors to perform such simulations using different codes. In such future model calculations, it would be important to provide simulation results and answers for:
・ Angular distribution of the prongs with respect to the beam axis. Also examine if model calculations reproduce events in which in the exit channel no charged particles are emitted within a forward cone covering an angle of 14˚.
・ An explanation why relativistic fragments (especially He-ions) from the first generation of ion-nucleus interactions are more efficient in inducing BURST events than normal primary relativistic ions.
Cite this paper
Hashemi-Nezhad, R., Brandt, R., Ditlov, V., Haiduc, M., Firu, E., Neagu, A.T., Ganssauge, E. and Westmeier, W. (2017) Further Studies of BURSTS and Spallation in High-Energy Heavy Ion Reactions. World Journal of Nuclear Sci- ence and Technology, 7, 35-57. http://dx.doi.org/10.4236/wjnst.2017.71004
References
- 1. Brandt, R., Ditlov, V., Haiduc, M., Firu, E., Neagu, A.T., Ganssauge, E., Hashemi-Nezhad, R. and Westmeier, W. (2015) Two Ways of High-Energy Heavy Ion Interactions: Spallation and Burst. World Journal of Nuclear Science and Technology, 5, 73-87.
https://doi.org/10.4236/wjnst.2015.52007 - 2. Westmeier, W., Brandt, R., Hashemi-Nezhad, R., Odoj, R., Ensinger, W., Zamani-Valasiadou, M. and Sosnin, A. (2012) Correlations in Nuclear Interactions between ECM/u and Unexplained Experimental Observables. World Journal of Nuclear Science and Technology, 2, 125-132.
https://doi.org/10.4236/wjnst.2012.24018 - 3. Khan, H.A., Jamil, K., Brandt, R., Friedlander, E. and Kraft, G. (1986) A Study of Clusters of Light Tracks in a Stack of CR-39 Exposed to 960MeV/u 238U. GSI-Scientific Report (GSI-86-1), Darmstadt, 104.
- 4. Ganssauge, E. (1987) Der Experimentelle Stand der Anomalonen-Forschung. Annalen der Physik, 11, 202-246.
https://doi.org/10.1002/andp.19874990306 - 5. Tolstov, K.D. (1991) Some Peculiarities of Relativistic Nucleus Collisions. International Journal of Radiation Applications and Instrumentation Part D: Nuclear Tracks and Radiation Measurements, 19, 657-664.
https://doi.org/10.1016/1359-0189(91)90288-s - 6. Ditlov, V.A., Dubinina, V.V., Krotkova, V.I., Pozharova, E.A., Smirnitzky, V.A., Brandt, R. and Ensinger, W. (2005) Study of Number of Black Prongs in Two Generations of Nuclear Interactions in Photoemulsions Irradiated by 72 GeV 22Ne. Radiation Measurements, 40, 448-459.
https://doi.org/10.1016/j.radmeas.2005.06.021 - 7. Ditlov, V.A., Dubinina, V.V., Krotkova, V.I., Pozharova, E.A., Smirnitzky, V.A., Brandt, R., Westmeier, W. and Ensinger, W. (2006) Distribution of Black Prong Numbers of Fragments Measured in Two Generations of Nuclear Interactions in Photoemulsion Irradiated with 72 GeV 22Ne. Unpublished, Presented as Poster at the 20th International Conference on SSNTD in Beijing.
- 8. Lerman, L. (2002) On the Symmetry of Nuclear Identity between Relativistic Primary and Secondary Fragments. Dissertation, Fachbereich Chemie, Philipps-Universität, Marburg. Digital Sign. 4° 2002/2015.
- 9. Haiduc, M., Firu, F. and Neagu, A.T. (2012) Internal Report from Bucharest Institute of Space Science. Unpublished, Bucharest.
- 10. Pelowitz, D.B. (2011) MCNPX User’s Manual. Version 2.7.0, Los Alamos National Laboratory, LA-CP-11-00438.
- 11. Hashemi-Nezhad, S.R., Brandt, R., Ditlov, V.A., Firu, E., Ganssauge, E., Haiduc, M., Neagu, A.T. and Westmeier, W. (2017) Monte Carlo Studies of the Interactions of Heavy Ions with Nuclear Emulsion. Nuclear Instruments and Methods in Physics Research Section A, 841, 72-86.
https://doi.org/10.1016/j.nima.2016.10.030 - 12. Dgbrowska, A., Holynski, R., Jurak, A., Olszewski, A.M., Szarska, A.T., Wilczynska, B., Wilczynski, H., Wolter, W., Wosiek, B. and Wozniak, K. (1993) Particle Production in Interactions of 200 GeV/Nucleon Oxygen and Sulfur Nuclei in Nuclear Emulsion. Physical Review D, 47, 1751-1761.
https://doi.org/10.1103/PhysRevD.47.1751 - 13. Ganssauge, E., Westmeier, W. and Brandt, R. (2013) Potential Correlations between Unexplained Experimental Observables and Hot Projectile-Fragments in the Primary Interaction above ECM/u ≈ 150 MeV. World Journal of Nuclear Science and Technology, 3, 155-161.
https://doi.org/10.4236/wjnst.2013.34026 - 14. Bannik, B.P., El-Naghy, A., Ibatov, R., Salomov, J.A., Shabratova, G.S., Sherif, M. and Tolstov, K.D. (1978) Central Collisions of Fast Particles with Heavy Nuclei. Zeitschrift für Physik A ,284, 283-286.
https://doi.org/10.1007/BF01406799 - 15. Tolstov, K.D. (1981 Complete Destruction of Heavy Nuclei by Hadrons and Nuclei. Zeitschrift für Physik A, 301, 339-342.
https://doi.org/10.1007/BF01421698 - 16. Brandt, R., Ditlov, V.A., Dwiwedi, K.K., Ensinger, W., Ganssauge, E., Guo, S., Haiduc, M., Hashemi-Nezhad, S.R., Khan, H.A., Krivopustov, M.I., Odoj, R., Pozharova, E.A., Smirnitzky, V.A., Sosnin, A.N., Westmeier, W. and Zamani-Valasiadou, M. (2008) Interactions of Relativistic Heavy Ions in Thick Heavy-Ele-ment Targets and Some Unresolved Problems. Physics of Particles and Nuclei, 39, 259-285.
https://doi.org/10.1134/S1063779608020044 - 17. Wan, J.-S., Ochs, M., Brandt, R., Schmidt, T., Langrock, E.-J., Vater, P., Abdullaev, I.G., Adam, J., Bamblevskij, V.P., Bradnova, V., Butsev, V.S., Geloviani, L.K., Golubev, P.I., Gridnev, T.G., Kalinnikov, V.K., Karachuk, J., Krivopustov, M.I., Kulakov, B.A., Sosnin, A.N., Perelygin, V.P., Priemyshev, A.N., Pronskikh, V.S., Stegailov, V.I., Zupko-Sitnikov, V.M., Adloff, J.C., Debeauvais, M., Modolo, G., Odoj, R., Phlippen, P.-W., Zamani, M., Dwivedi, K.K. and Wilson, B. (1997) Transmutation of Radioactive Waste with the Help of Relativistic Heavy Ions. JINR-E1-97-349.