World Journal of Nuclear Science and Technology
Vol.06 No.04(2016), Article ID:70947,15 pages
10.4236/wjnst.2016.64023
Studies on Production Planning of Dispersion Type U3Si2-Al Fuel in Plate-Type Fuel Elements for Nuclear Research Reactors
Miguel Luiz Miotto Negro1, Michelangelo Durazzo1, Marco Aurélio de Mesquita2, Elita Fontenele Urano de Carvalho1, Delvonei Alves de Andrade1
1Instituto de Pesquisas Energéticas e Nucleares (Nuclear and Energy Research Institute), São Paulo, Brazil
2Escola Politécnica da Universidade de São Paulo (Polytechnic School of São Paulo University), São Paulo, Brazil
Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: August 26, 2016; Accepted: September 25, 2016; Published: September 28, 2016
ABSTRACT
Several fuel plants that supply nuclear research reactors need to increase their production capacity in order to meet the growing demand for this kind of nuclear fuel. After the enlargement of the production capacity of such plants, there will be the need of managing the new production level. That level is usually the industrial one, which poses challenges to the managerial staff. Such challenges come from the fact that several of those plants operate today on a laboratorial basis and do not carry inventory. The change to the industrial production pace asks for new actions regarding planning and control. The production process based on the hydrolysis of UF6 is not a frequent production route for nuclear fuel. Production planning and control of the industrial level of fuel production on that production route is a new field of studies. The approach of the paper consists in the creation of a mathematical linear model for minimization of costs. We also carried out a sensitivity analysis of the model. The results help in minimizing costs in different production schemes and show the need of inventory. The mathematical model is dynamic, so that it issues better results if performed monthly. The management team will therefore have a clearer view of the costs and of the new, necessary production and inventory levels.
Keywords:
Fabrication of Uranium Silicide Fuel, Nuclear Research Reactors, Production Planning and Control

1. Introduction
The pacific use of nuclear technology is expanding worldwide [1] [2] . That expansion leads to an increase in the study of nuclear sciences and in the use of nuclear research reactors. That is so, because research reactors are responsible for a relevant portion of the generation of knowledge on nuclear technology as well as for a part of the pacific use of this technology [3] - [6] . The expansion in the use of nuclear research reactors causes the demand for their fuel to increase. In order to meet the increasing demand for nuclear fuel for research reactors, we need to study how to enhance the production capacity of this class of fuel. That is an extensive task, so that we will not address that issue in this paper. However, once the production capacity has been enlarged to a level high enough to meet the new demand, we will need to plan and control that production. That is the subject of this paper.
Below is a list of the main characteristics of the production of nuclear fuels for research reactors:
・ laboratory scale,
・ exclusive for one reactor,
・ production facility located near the corresponding user, and
・ non-commercial transactions.
Nowadays several facilities that produce nuclear fuel for research reactors are having their production capacities expanded [1] [2] [5] . This fact underlines the importance of planning and controlling the new, larger production level in order to assure the production processes are efficiently performed and that the fuel accomplishes customers’ requirements [7] - [9] .
There are several kinds of nuclear fuels for research reactors and each fuel type has its own productive processes [10] . Besides, some different production processes may lead to the same fuel type. These facts point out the need of selection of one fuel type and one production route in order to set the scope of this paper.
The fuel type chosen for this study is the uranium silicide dispersed in aluminum, known as dispersion type U3Si2-Al fuel. We adopted its maximum enrichment as 20% of the isotope 235U, which is named Low Enriched Uranium (LEU) and which complies with the Reduced Enrichment for Research and Test Reactors (RERTR) Program [11] . This way, the selected fuel type may be referred to as LEU U3Si2-Al fuel. We opted for LEU U3Si2-Al fuel because of its wide use in research reactors, its good capacity of uranium loading and its excellent performance [12] - [14] .
The production of LEU U3Si2-Al fuel may be divided into two large sets of processes. The first set comprises the chemical processes and the second set, the metallurgical processes. Both processes sets may have different modes. But the chemical processes are the ones that have the bigger variability [15] . This fact imposes the selection of one specific chemical route in order to set limits for this work. We chose the chemical track that includes the hydrolysis of uranium hexafluoride (UF6) for the ensuing reasons:
・ that path stands out for its simplicity and relative safety;
・ it is used to produce small quantities of the intermediate products and
・ the rising demand for nuclear fuels for research reactors will probably affect facilities operating that production scheme.
The facts exposed so far underline the convenience of having a safe and reliable planning and control system for an increased production of LEU U3Si2-Al fuel, whose fabrication process includes UF6 hydrolysis. The design of such a system is an extensive task that is not within the limits of this paper. Thus, the objective of this paper is to develop the first parts of what should be the production planning and control system of a plant that produces LEU U3Si2-Al fuel, on the route that uses UF6 hydrolysis.
On the other hand, there is a plant in São Paulo, Brazil, which produces LEU U3Si2-Al fuel for research reactors and performs UF6 hydrolysis. That factory belongs to IPEN, Nuclear and Energy Research Institute, which is part of CNEN, Brazilian National Commission on Nuclear Energy. IPEN’s plant has been producing reliable nuclear fuel for the research reactor IEA-R1, Atomic Energy Institute-Reactor 1, for decades. The IEA-R1 reactor also belongs to IPEN.
Among various analytical instruments available to perform planning and control, in this study the option was made for the creation of a mathematical model for linear optimization. We used real data from IPEN’s fuel plant to run the model and to conduct its sensitivity analysis, obtaining useful results.
2. Literature Review
2.1. Nuclear Engineering
We supposed that the plant would produce only one product. That product is a Plate-Type Fuel Element (PTFE) containing LEU U3Si2-Al fuel. The raw materials and intermediate products for the production of LEU U3Si2-Al fuel are well known and can be found in several references [11] [13] [16] [17] . For this reason, in this study we do not enter in details for this item.
In addition to the fuel itself, IPEN’s nuclear fuel plant also produces PTFE containing LEU U3Si2-Al fuel for the research reactor IEA-R1. The FE produced by IPEN’s nuclear fuel plant is exclusively used in the IEA-R1 reactor and was designed specifically for that reactor. As previously mentioned, IPEN’s nuclear fuel plant has been producing this FE for decades. Consequently, the design of that product is well established as are the production processes necessary for its fabrication. This FE is the typical PTFE used by most research reactors worldwide. It is made by the assembly of several fuel plates (FP) and other mechanical components [18] . Its raw materials and productive processes are defined and set [15] . Thus, we do not expose details of the product as well as of its productive processes in this paper.
The design of the PTFE for the reactor IEA-R1 is the database for the cost estimate of Section 4 of this work. That design is not published, but several references point out the main characteristics of a typical PTFE [17] [19] - [21] . Such main characteristics provide data, which are very similar to the ones we used in the cost estimation section of this study.
2.2. Production Planning and Control
Many of the previously mentioned questions are studied by the area of operations management [7] - [9] [22] - [25] . That body of knowledge lies on the interface between natural and social sciences [26] . Therefore, any manufacturing plant is strongly influenced by the decisions of its managers. In other words, managers’ decisions set up an important part of the work of all systems of any factory. Such decisions translate into data needed for this paper, as we will present up ahead. Furthermore, operations management deals with the design, analysis and improvement of production systems. One of the elements that form such systems is planning and control [7] [9] [22] [23] .
The area of planning and control has several ways and tools to perform its tasks. A very common way is called Operations Research (OR), which is a scientific approach for problem solving of complex systems management. Nowadays OR is used in activity fields as different as agriculture, education, industry, transportation and finance [27] - [29] . Among several analytical instruments available in OR, in this study the option was made for the creation of a mathematical model for linear optimization, as previously mentioned. The creation, the conditions and the supporting literature of the mathematical model are exposed in Section 5. The data needed to run the model come from the cost estimate of a PTFE. That cost estimate, its supporting literature and its primary data sources and detailed in Section 4.
3. Methods
The methodology used in this paper is divided in two parts and each part is detailed in separated sections. Ensuing is an overview of those two parts.
Estimation of cost
The basis for the analysis conducted in this paper is the cost, due to its importance in any production process. Thus, the cost is the basis that supports this study. This is the reason for which we need to calculate the value of the production cost of a typical PTFE. However, calculating the exact cost of any product is an extensive task, which would exceed the limits of this paper. That means that we work with cost estimates. Such estimates are enough to accomplish the objectives of this study, since this study aims to be a first approach in the design of a system for production planning and control.
Data processing
After estimating the costs, we need to evaluate their behavior along the time. Thus, we created a mathematical model for the minimization of the total production cost. We used the data and assumptions from previous and posterior sections to run the model for one production scheme, as presented in Sections 5 and 6. We varied some parameters of that production scheme in order to study four other production schemes. That variation constitutes the sensitivity analysis of the model, thus providing information on the precision of the model.
4. Estimation of Cost
In this section we present an estimation of costs for the production of one typical PTFE.
Aluminum
We start by a cost estimation of the raw materials used in one typical PTFE. The main material of that FE is aluminum and Table 1 shows the aluminum components of a typical PTFE, the average dimensions of those components and the gross volume of each component [11] [13] [15] - [19] [21] .
Table 2 presents the next steps of the aluminum cost estimate. Below is an explanation of how the columns of Table 2 were obtained.
・ The second column shows the number of pieces of each component necessary to build one PTFE [11] [13] [15] - [19] [21] ;
・ We used the average density of Aluminum as 2700 kg/m3 [30] . This value was multiplied to the volumes from Table 1 and the results are exposed in the third column of Table 2;
・ The forth column is the result of multiplying columns 2 and 3;
・ The fifth column shows the applied engineering factors to account for extra material needed for the production of each component [31] [32] and
・ The last column is the multiplication of the fifth column by 30%, which is the average percentage of aluminum waste for all processes needed to build one PTFE [33] .
Table 1. Components of a plate type FE.
Table 2. Calculation follow-up.
Adding the final column of Table 2 results in 13.4 kg of aluminum as an average weight of this material needed to produce one typical PTFE. The cost of aluminum is US$ 5.22 per kg [30] for purchasing large quantities FOB USA ports. Therefore, we added a factor of 100% in order to account for small quantities and for Brazilian taxes, so that the aluminum cost used in this paper is US$ 10.44 per kg. Thus our total aluminum cost is US$ 139.90 per PTFE and we name it Cost 1.
Other raw materials
Table 3 presents other raw materials considered in this paper, the quantities of them usually needed for the production of one PTFE, their costs, the references for the mentioned costs and their costs in one PTFE.
The values obtained from the references of Table 3 are costs for large quantities FOB USA ports. The prices presented in Table 3 include a factor of 100% on the references’ prices in order to account for small quantities and Brazilian taxes. Adding the last column of Table 3 results in US$ 1361.95, named Cost 2.
Purchased parts
Some parts of a typical PTFE are not produced in the same plant that processes the nuclear fuel and the PTFE itself. Such parts are usually made with the same aluminum of the rest of the PTFE. In order to estimate these costs, we set manufacturing factors over the aluminum content of each purchased part and expose them in Table 4 [31] - [33] .
The costs presented in Table 4 are an estimate of the manufacturing cost of the parts mentioned in that table. Such costs do not include the costs of the raw materials needed for the manufacturing of those parts, which were presented in Table 2 and Table 3. The last column of Table 4 was obtained multiplying its third column to its four column to US$ 10.44, which is the price per kilogram of aluminum. Adding the last
Table 3. Other raw materials.
Table 4. Purchased parts.
column of Table 4 results in US$ 214.23, named Cost 3.
Energy
The main type of energy used in the production processes of IPEN’s fuel plant is electrical. For this reason, we will only consider that kind of energy in this paper. Table 5 presents the main equipment used, its power, the times each apparatus works to produce one PTFE [15] [18] and the cost.
The last column of Table 5 was obtained multiplying its third column to its four column to US$ 1.73, which is the price per kWh of electrical energy [40] . Adding the last column of Table 5 results in US$ 1.109.62, which is the estimate of cost of electrical energy used for production of one PTFE. This cost does not account for base and maintenance energy consumptions, which affect the cost of the PTFE. Ensuing we explain the procedures adopted to estimate the cost of those parts of energy consumption.
Firstly, we must address the yearly fuel demand, which we set as 100 PTFE. This value is the sum of the following three factors:
・ There is a project to build a new nuclear research reactor in Brazil in the near future. The new reactor will belong to CNEN, imposing its fuel to be supplied by IPEN’s factory according to Brazilian regulations. That new reactor will demand 60 PTFE per year;
・ IPEN’s nuclear fuel plant will continue to supply 10 PTFE per year to the IEA-R1 reactor and
・ There is the possibility of exporting approximately 30 PTFE per year.
Besides, we consider as base energy consumption the energy the factory uses independently of production, i.e., for lightning, security and office. The basic consumption exists for the whole year and is estimated in 1.2% of the energy used for production each month. Thus the base consumption in one year is 12 × 1.2 = 14.4% of the total year demand of energy for production of 100 PTFE.
Finally, we name maintenance energy consumption the energy the factory uses for the maintenance activities held during two months each year. The maintenance consumption is estimated in 3% of the energy used for production each month. Thus the maintenance energy consumption in one year is (2 × 3)/10 = 6% of the total year demand of energy for production of 100 PTFE.
The values of energy consumption for both maintenance and base refer to the production of 100 PTFE, considering production in 10 months and maintenance in two months. The addition of those two factors results in approximately 14.4% + 6% = 20% increase in the cost of energy to produce one PTFE. Thus, we added 20% to the cost of
Table 5. Electrical energy.
electrical energy for one PTFE and obtained US$ 1331.55 as the total energy cost per PTFE, named Cost 4.
Labor
The basis for our estimate of labor cost is the monthly salary of a Technician on the top of the Career of Technological Development. That salary was R$ 7902.14 [41] in July 2015 what makes US$ 2507.94 according to the exchange rate of US$ 1.00 = R$ 3.15 [42] . The expenditure of the organization with such an employee is approximately 80% more than the mentioned salary, due to Brazilian taxes and labor laws [43] [44] . Thus, the cost of one Technician is approximately US$ 5414.29 per month or US$ 28.21 per hour, assuming 160 working hours per month.
IPEN’s nuclear fuel plant is divided in four work centers, each one having the number of employees exposed in Table 6. The third column of Table 6 was obtained multiplying the number of employees of each work center to the hourly cost of one employee. The fourth column of Table 6 displays the amount of the time each work center needs to perform their tasks in order to produce one PTFE [15] [18] [21] . The fifth column of Table 6 was calculated multiplying its column four to its column three.
Adding the last column of Table 6 results in US$ 20,321.37, which is the estimate of cost for production of one PTFE. This value does not account for the cost of labor during the two months reserved for maintenance.
Since the mentioned 100 PTFE are all produced in the period of ten months within the year and since the cost of labor happens all 12 months, so there is an approximate addition of (12/10) − 1 = 20% in the cost of labor for the total yearly production. Thus, we added 20% to the labor cost for one PTFE and obtained US$ 24,385.64 as the total labor cost per PTFE, named Cost 5.
Environmental and total costs
The CER (Critical Environmental Rate) is a coefficient for account for environmental cost for different human activities and it may vary substantially [45] . This way, we assumed the value of 10% as the CER to account for environmental cost for nuclear PTFE production. Thus, Table 7 shows the addition of costs 1 through 5 mentioned above, its increase in 10% to account for environmental costs and the final estimation of cost.
5. Data Processing
Mathematical models for linear optimization have wide use in agriculture, production planning and control, logistics, telecommunications, finance, transportation and many other areas [23] [27] - [29] [46] - [53] . The following model was adapted from the litera-
Table 6. Labor.
Table 7. Estimate of the total PTFE cost.
ture [46] [48] [50] - [52] [54] and represents the enlarged production of IPEN’s nuclear fuel plant. The model looks for the monthly production level, which will minimize the total annual production cost. For that reason, the unknown variables are the monthly production quantities of PTFE. The unknown variables are called decision variables [46] [48] [50] - [52] [54] and they are the key data for production planning. Thus, our decision variable is:
xt = quantity of PTFE to be produced in month t
That amount will never be negative, so that:
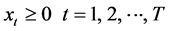
The boundary conditions of the model are presented below.
・ The plant produces only one product;
・ It is desired to plan its production for T periods of time;
・ The time period was set as one month;
・ The model was made for one year of planning, so that T = 12 months;
・ Demand is known every month;
・ The resources required for production are limited, renewable and there is enough availability of them in the beginning of each month;
・ There is the possibility of keeping inventory from one month to the other and
・ Production stops for two months per year for maintenance. This way: x1 = x7 = 0
The model’s goal is to minimize the production cost. Table 8 presents the definitions of the input variables, their symbols, and the values adopted to run the model.
We supposed that the cost of holding one PTFE in inventory each month is R = 1.5% of the production cost in the same month. We adopted the number of PTFE held each month as the average of the beginning and ending inventory for the month. We also assumed that the beginning inventory in any month is equal to the ending inventory from the previous month. Thus, the inventory cost (IC) is expressed by Equation (1):
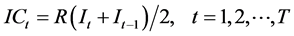 (1)
(1)
The Objective Function must reflect the goal of the model, i.e., the Objective Function must be minimizing the total annual production cost. That cost is the sum of the
Table 8. Input variables.
product of the cost to produce one PTFE to the total production plus the inventory cost. Thus the Objective Function is expressed by Equation (2):
Minimize 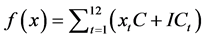 (2)
(2)
The Objective Function must obey following constraints, according to the previous assumptions:
Inventory constraints
IBt = IEt−1 t = 1, 2, ∙∙∙, T;
IEt = IEt−1 + xt − dt t = 1, 2, ∙∙∙, T and
Imint ≤ IEt ≤ lmaxt t = 1, 2, ∙∙∙, T
Replacing the adopted values:
1 ≤ IEt ≤ 6 t = 1, ..., 12;
Production capacity constraints
Production yield cannot be bigger than production capacity, i.e.:
xt ≤ PCt t = 1, 2, ..., T
Replacing the adopted values:
For any month xt ≤ 12
For one year xt ≤ 120
Demand meeting constraints
xt + IEt−1 ≥ dt or xt + IEt−1 − dt ≥ 0.
But we defined xt + IEt−1 − dt = IEt.
Thus to guarantee that the demand will be met, it is enough to impose:
Imint ≤ IEt ≤ lmaxt t = 1, 2, ..., T
Therefore the complete model has the following formulation:
Minimize 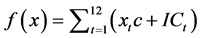
Subject to:
IEt = IEt−1 + xt − dt t = 1, 2, ∙∙∙, 12
1 ≤ lEt ≤ 6 t = 1, 2, ∙∙∙, 12;
xt ≤ 12 t = 1, 2, ∙∙∙, 12;
x1 = x7 = 0
xt ≥ 0 t = 1, 2, ∙∙∙, 12
The model is linear and has more equations than unknown variables, thus having many possible solutions. The most common way of finding the optimal solution is the Simplex Method, which is widely studied in the literature [23] [28] [46] [48] [51] [52] [54] - [57] . The output of the model are the monthly levels of production, inventory and costs, as well as the minimized annual total production cost. Such outputs are calculated at the same time that the monthly and yearly demands are met.
6. Results and Conclusions
Table 9 shows the results of the model for the input data exposed in Section 5. The explanation of the contents of columns 2 to 5 is as follows:
・ Column 2: Inventory at the beginning of month t, IBt.
・ Column 3: Monthly production, xt.
・ Column 4: Monthly demand, dt.
・ Column 5: Inventory at the end of month t, IEt.
Columns 2 to 5 of Table 9 are given in PTFE number. Column 4 of that table contains data we input in it, in such a way to simulate the variations of demand within one year. We also set x1 = x7 = 0 in column 3 of Table 9 in order to account for the production stops for maintenance. All other values of Table 9 are the results produced by running the model, both in PTFE number as well as in US$, where appropriate.
Table 9. Model’s results.
Table 10. Sensitivity analysis.
From Table 9 we calculated the yearly average of inventory in the beginning of the month as 1.83 PTFE and in the end of the month as 1.5 PTFE. The cost of carrying that inventory is 0.3% of the total production cost. That value is probably lower than the cost the plant would have, if it would lose customers because of lack of inventory. This way, we assume it is better to carry inventory.
Table 9 also gives the values of monthly production, so that the plant staff can plan in advance how to manage their resources in order to meet the demand month by month. Besides, the model is dynamic, so that it should be ran every month with real data from the previous month. The monthly run of the model will give updated information to the managerial staff, thus providing more precision to the support of their decisions in planning and controlling the production.
As mentioned before, Table 9 resulted from running the model with data from previous sections. However, it is interesting to evaluate the response of the model for some different data, i.e., it is important to conduct the sensitivity analysis of the model. This way we varied the minimum and maximum inventory levels and we kept all other data as they are in Section 5. We did it in four different ways, creating four new production schemes. Table 10 shows the total annual cost returned by the model after running each one of the new production schemes. Scheme number 2 in Table 10 corresponds to the results from Table 9.
From scheme 1 to scheme 4 in Table 10 the total cost grows as the inventory levels also do. However, a decrease in inventory level from scheme 4 to 5 led to an increase in costs. These results indicate the need of a deeper sensitivity analysis in order to look for an optimized inventory level. That would lead to the need of a more complex model and other data, what could be accomplished in future works.
Cite this paper
Negro, M.L.M., Durazzo, M., de Mesquita, M.A., de Car- valho, E.F.U. and de Andrade, D.A. (2016) Studies on Production Planning of Dispersion Type U3Si2-Al Fuel in Plate-Type Fuel Elements for Nuclear Research Reactors. World Journal of Nuclear Science and Te- chnology, 6, 217-231. http://dx.doi.org/10.4236/wjnst.2016.64023
References
- 1. Chen, T., Chen, G., Yang, S., Zhao, Y., Ha, Y. and Ye, Z. (2015) Recent Developments in the Application of Nuclear Technology on Agro-Food Quality and Safety Control in China. Food Control, 1-7.
http://dx.doi.org/10.1016/j.foodcont.2015.08.034 - 2. Cheng, X., Batta, A., Bandini, G., Roelofs, F., Van Tichelen, K., Gerschenfeld, A., et al. (2015) European Activities on Crosscutting Thermal-Hydraulic Phenomena for Innovative Nuclear Systems. Nuclear Engineering and Design, 290, 2-12.
http://dx.doi.org/10.1016/j.nucengdes.2014.11.007 - 3. Hong, S., Bradshaw, C.J.A. and Brook, B.W. (2014) Nuclear Power Can Reduce Emissions and Maintain a Strong Economy: Rating Australia’s Optimal Future Electricity-Generation Mix by Technologies and Policies. Applied Energy, 136, 712-725.
http://dx.doi.org/10.1016/j.apenergy.2014.09.062 - 4. Khajvand, N., Mirvakili, S.M. and Faghihi, F. (2016) Cold Neutron Source Conceptual Designing for Tehran Research Reactor. Annals of Nuclear Energy, 92, 407-412.
http://linkinghub.elsevier.com/retrieve/pii/S0306454916300664 - 5. Choo, K.N., Cho, M.S., Yang, S.W. and Park, S.J. (2014) Contribution of Hanaro Irradiation Technologies to National Nuclear R&D. Nuclear Engineering and Technology, 46, 501-512.
http://dx.doi.org/10.5516/NET.07.2014.006 - 6. Pegonen, R., Bourdon, S., Gonnier, C. and Anglart, H. (2016) Hot Fuel Element Thermal-Hydraulics in the Jules Horowitz Reactor. Nuclear Engineering and Design, 300, 149-160.
http://linkinghub.elsevier.com/retrieve/pii/S0029549316000510 - 7. Slack, N., Brandon-Jones, A. and Johnston, R. (2013) Operations Management. 7th Edition, Prentice Hall, Upper Saddle River.
- 8. Stevenson, W.J. (2014) Operations Management. 12th Edition, McGraw-Hill Education, New York.
- 9. Krajewski, L.J., Malhotra, M.K. and Ritzman, L. (2015) Operations Management: Processes and Supply Chains Plus. 11th Edition, Prentice Hall, Upper Saddle River.
- 10. Nasir, R., Butt, M.K., Mirza, S.M. and Mirza, N.M. (2015) Effect of High Density Dispersion Fuels on Transient Behavior of MTR Type Research Reactor under Multiple Reactivity Transients. Progress in Nuclear Energy, 85, 511-517.
http://www.sciencedirect.com/science/article/pii/S0149197015300482 - 11. Snelgrove, J.L., Doraagala, R.F., Hofraan, G.L. and Wiencek, T.C. (1987) The Use of U3Si2 Dispersed in Aluminum in Plate-Type Fuel Elements for Research and Test Reactors. ANL/RERTR/TM-11. Argonne, IL.
http://dx.doi.org/10.2172/5688807 - 12. Finlay, M.R., Hofman, G.L. and Snelgrove, J.L. (2004) Irradiation Behaviour of Uranium Silicide Compounds. Journal of Nuclear Materials, 325, 118-128.
http://dx.doi.org/10.1016/j.jnucmat.2003.11.009 - 13. Gan, J., Keiser, D.D., Miller, B.D., Jue, J.F., Robinson, A.B., Madden, J.W., et al. (2011) Microstructure of the Irradiated U3Si2/Al Silicide Dispersion Fuel. Journal of Nuclear Materials, 419, 97-104.
http://dx.doi.org/10.1016/j.jnucmat.2011.07.030 - 14. Kim, Y.S., Hofman, G.L., Rest, J. and Robinson, A.B. (2009) Temperature and Dose Dependence of Fission-Gas-Bubble Swelling in U3Si2. Journal of Nuclear Materials, 389, 443-449.
http://dx.doi.org/10.1016/j.jnucmat.2009.02.037 - 15. Saliba-Silva, A.M., de Carvalho, E.F.U., Riella, H.G., Durazzo, M. and Urano de Carvalho, E.F. (2011) Chapter 2: Research Reactor Fuel Fabrication to Produce Radioisotopes. In: Singh, N., Ed., Radioisotopes-Applications in Physical Sciences, InTech [Internet].
http://www.intechopen.com/books/radioisotopes-applications-in-physical-sciences
http://www.intechopen.com/books/radioisotopes-applications-in-physical-sciences/research-reactor-fuel-fabrication-to-produce-radioisotopes - 16. Nuclear Energy Agency (2000) Nuclear Energy in a Sustainable Development Perspective. Organisation for Economic Co-Operation and Development.
- 17. Simnad, M.T. (1981) Perspective on Research Reactors and Their Fuel Elements. Journal of Nuclear Materials, 100, 78-92.
http://dx.doi.org/10.1016/0022-3115(81)90523-7 - 18. Durazzo, M. and Riella, H.G. (2015) Procedures for Manufacturing Nuclear Research Reactor Fuel Elements. OmniScriptum GmbH & Co. KG., Saarbrücken.
- 19. Olivares, L. (2013) Manufacture of Nuclear Fuel Elements in Chile. Chilean Nuclear Energy Commission.
- 20. Wachs, D.M., Clark, C.R. and Dunavant, R.J. (2008) Conceptual Process Description for the Manufacture of Low-Enriched Uranium-Molybdenum Fuel. Report No. INL/EXT-08-13840, Idaho Falls.
- 21. IAEA (2000) Advanced Methods of Process/Quality Control in Nuclear Reactor Fuel Manufacture. 18-22.
- 22. Chase, R. and Jacobs, R. (2013) Operations and Supply Chain Management. 14th Edition, McGraw-Hill Higher Education, New York.
- 23. Hopp, W.J. and Spearman, M.L. (2001) Factory Physics: Foundations of Manufacturing Management. Shelstad, J.J., Ed., 2nd Edition, Irwin/McGraw-Hill, New York.
- 24. Neumann, C. and Scalice, R.K. (2015) Projeto de Fábrica e layout. Elsevier, Rio de Janeiro.
- 25. Slack, N., Chambers, S., Johnston, R. and Betts, A. (2008) Operations and Process Management. 2nd Edition, Prentice Hall, Upper Saddle River.
- 26. Miguel, P.C. (2012) Metodologia de Pesquisa em Engenharia de Produção e Gestão de Operações. Teixeira, I., Ed., 2nd Edition, Elsevier, São Paulo.
- 27. Shrader, C.R. (2009) History of Operations Research in the United States Army. US Army, Washington DC.
- 28. Winston, W.L. and Goldberg, J.B. (2004) Operations Research: Applications and Algorithms. 4th Edition, Cengage Learning, Belmont.
- 29. Gass, S.I. and Assad, A.A. (2005) An Annotated Timeline of Operations Research. Springer, Berlin, 125.
http://ebooks.kluweronline.com - 30. Midwest Steel and Aluminum (2016) Aluminum Prices. New Hope, Minnesota, 43.
https://www.midweststeelsupply.com/store/6061aluminumplate - 31. Martins, J.A.P. and de Elias, M.A. (2012) Fabricação a Partir Da Colagem De Pastilhas De Aço Sinterizado Com Tecido De Aramida.
- 32. Melorose, J., Perroy, R. and Careas, S. (2015) Implementation of the Global Efficiency Equipment in the Machining Sector. Statew. Vol. 1, Statewide Agricultural Land Use Baseline, 163-172.
- 33. Soares, F. and Costa, D.A. (2014) Ganhos de produtividade e sistemas toolsetter laser.
- 34. EIA (2013) 2013 Uranium Marketing Annual Report. EIA, 1-40.
http://www.eia.gov/uranium/marketing/pdf/2013umar.pdf - 35. Statista GmbH (2016) US Silicon Price by Type. Hamburg, 56.
http://www.statista.com/statistics/301564/us-silicon-price-by-type/ - 36. InfoMine Inc (2016) Metal Prices—Magnesium. Vancouver, 37.
http://www.infomine.com/investment/metal-prices/magnesium/ - 37. University of Illinois at Urbana-Champaign (2007) So-Called “Cheap” Liquid Nitrogen. Urbana, 164.
https://van.physics.illinois.edu/qa/listing.php?id=1685 - 38. ICIS-RELX Group (2016) Chemical Profile: Nitric Acid. London, 72.
http://www.icis.com/resources/news/2008/05/19/9124327/chemical-profile-nitric-acid/ - 39. Synth (2016) Reagentes Analiticos/cloreto de estanho. Diadema, 54.
http://www.lojasynth.com/reagentes-analiticosmaterias-primas/reagentes-analiticosmaterias-primas/cloreto-de-estanho-oso-2h2o-p-a-a-c-s - 40. AES Eletropaulo (2016) Tarifas energia elétrica—Setor público. São Paulo, 04.
https://www.aeseletropaulo.com.br/poder-publico/prazos-e-tarifas/conteudo/tarifa-de-energia-eletrica - 41. Silva MCR da, Maria Vilani Maia de Freitas (2015) Tabela de Remuneração dos Servidores Públicos Federais Civis e dos Ex-Territórios. Técnico da Carreira Desenvolv, Tecnológico.
http://www.planejamento.gov.br/assuntos/gestao-publica/arquivos-e-publicacoes/tabela-de-remuneracao-1 - 42. Banco Central do Brasil (2016) Conversão de moedas. Brasília, 01.
http://www4.bcb.gov.br/pec/conversao/conversao.asp?id=convmoeda - 43. Rocha, W. (1992) Custo de mão-de-obra e encargos sociais. Caderno de Estudos, 1-26.
http://dx.doi.org/10.1590/S1413-92511992000100004 - 44. Manzano, M.P.F. (1996) Custo de demissão e proteção do emprego no brasil. Cris. e Trab, no Bras, Mod. ou volta ao passado, 253-268.
- 45. Almansa, C. and Martinez-Paz, J.M. (2011) What Weight Should Be Assigned to Future Environmental Impacts? A Probabilistic Cost Benefit Analysis Using Recent Advances on Discounting. Science of the Total Environment, 409, 1305-1314.
http://dx.doi.org/10.1016/j.scitotenv.2010.12.004 - 46. Arenales, M., Armentano, V., Morabito, R. and Yanasse, H. (2007) Pesquisa Operacional. Campus Editora, Rio de Janeiro.
- 47. Aziz, R.F. (2014) RPERT: Repetitive-Projects Evaluation and Review Technique. Alexandria Engineering Journal, 53, 81-93.
http://dx.doi.org/10.1016/j.aej.2013.08.003 - 48. Brandimarte, P. and Villa, A. (1995) Advanced Models for Manufacturing Systems Management. Geymonat, G., Ed., CRC Press Inc., Boca Raton.
- 49. Kunsch, P.L. and Teghem Jr., J. (1987) Nuclear Fuel Cycle Optimization Using Multi-Ob-jective Stochastic Linear Programming. European Journal of Operational Research, 31, 240-249.
http://dx.doi.org/10.1016/0377-2217(87)90028-2 - 50. Paterson, C., Kiesmüller, G., Teunter, R. and Glazebrook, K. (2011) Inventory Models with Lateral Transshipments: A Review. European Journal of Operational Research, 210, 125-136.
http://dx.doi.org/10.1016/j.ejor.2010.05.048 - 51. Pinedo, M.L. (2005) Planning and Scheduling in Manufacture and Services. Glynn, P.W. and Robinson, S.M., Eds., Springer, New York.
- 52. Ragsdale, C. (2012) Spreadsheet Modeling & Decision Analysis. McCormick, C.J. and Kubale, M., Eds., 6th Edition, South-Western Cengage Learning, Mason.
- 53. Tatterson, J. (1974) PERT, CPM and the Export Process. Omega, 2, 421-426.
http://dx.doi.org/10.1016/0305-0483(74)90036-X - 54. Pinedo, M.L. (2008) Scheduling. Springer, New York.
- 55. Duckworth, W.E., Gear, A.E. and Lockett, A.G. (2008) A Guide to Operational Research. Springer, New York.
- 56. Eglese, R.W.E. and Rand, G.K. (1977) Developments in Operational Research. A Volume in Frontiers of Operational Research and Applied Systems Analysis. Elsevier, Lancaster.
- 57. Van der Veen, B. (1967) Introduction to the Theory of Operational Research. Springer-Verlag Berlin.
http://dx.doi.org/10.1007/978-3-662-42424-7


